2.6等腰三角形 同步专题提升训练 2021-2022学年青岛版八年级数学上册 (word版含答案)
文档属性
| 名称 | 2.6等腰三角形 同步专题提升训练 2021-2022学年青岛版八年级数学上册 (word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 231.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览




文档简介
2021-2022学年青岛版八年级数学上册《2.6等腰三角形》 同步专题提升训练(附答案)
一.选择题
1.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
2.等腰三角形的一个内角是68°,则顶角是( )
A.68° B.44° C.68°或44° D.68°或112°
3.如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN或直线PQ上找一点C,使△ABC是等腰三角形,则这样的C点有( )
A.3个 B.4个 C.7个 D.8个
4.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
5.如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分别交AB、AC于点E、F,若EF=2DF,则AB的长为( )
A.4 B.6 C.8 D.10
6.如图,已知△ABC中,AB=AC,∠A=36°;BD平分∠ABC交AC于点D,点E是边AB上的一点,且满足ED=EA;过点D作DF∥CB交AB于点F,则图中等腰三角形的个数为( )
A.6个 B.7个 C.8个 D.9个
7.等边△ABC的两条角平分线BD和CE交于点I,则∠BIC的度数是( )
A.60° B.115° C.120° D.130°
8.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
二.填空题
9.如果等腰三角形有两条边长分别为2cm和3cm,那么它的周长是 .
10.如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,则BC= cm
11.如果等腰三角形的两内角度数相差45°,那么它的顶角度数为 .
12.△ABC中,∠B=50°,当∠C= 时,△ABC是等腰三角形.
13.如图,在△ABC中,∠C=90°,AC=3,BC=4,动点P从点B出发以每秒1个单位长度的速度沿B→A匀速运动;同时点Q从点A出发同样的速度沿A→C→B匀速运动.当点P到达点A时,P、Q同时停止运动,设运动时间为t秒,当t为 时,以B、P、Q为顶点的三角形是等腰三角形.
14.如图,∠C=2∠B,AD⊥BC,AC=5,CD=3,则BC= .
15.如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP= 度.
16.如图,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是 .
三.解答题
17.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长.
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
18.(1)如图①,在△ABC中,BD平分∠ABC,过点D作ED∥BC.指出图中的等腰三角形,并说明理由.
(2)如图②,在△ABC中,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC.证明:EF=BE+CF.
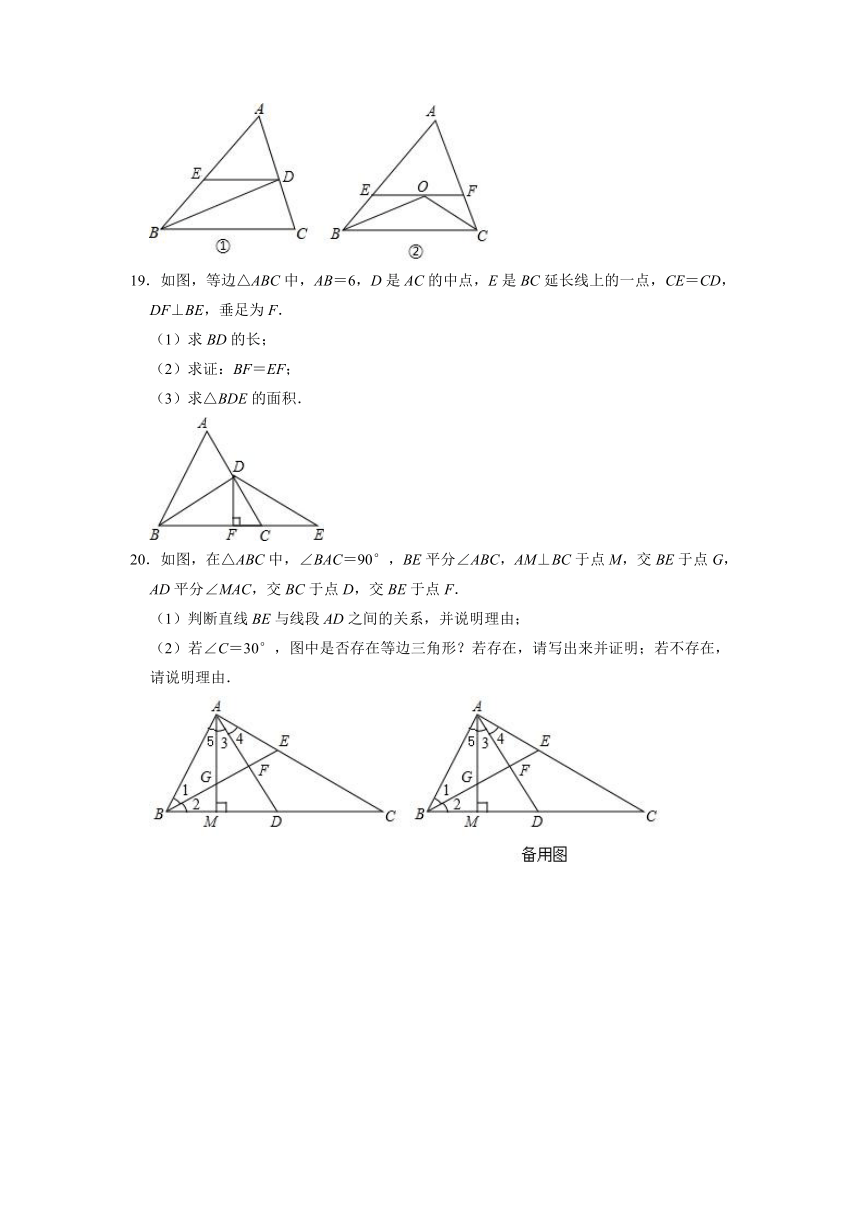
19.如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF;
(3)求△BDE的面积.
20.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.
参考答案
1.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
2.解:若顶角是68°,则结论显然;
若底角是68°,则顶角=180°﹣68°×2=44°.
故选:C.
3.解:使△ABC是等腰三角形,
当AB当底时,则作AB的垂直平分线,交PQ,MN的有两点,即有两个三角形.
当让AB当腰时,则以点A为圆心,AB为半径画圆交PQ,MN有三点,所以有三个.
当以点B为圆心,AB为半径画圆,交PQ,MN有三点,所以有三个.
所以共8个.
故选:D.
4.解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
5.解:如图,延长AD,BC交于点G,
∵BD平分∠ABC,
∴∠ABD=∠GBD,
∵AD⊥BD于点D,
∴∠ADB=∠GDB=90°,
又∵BD=BD,
∴△ABD≌△GBD(ASA),
∴AB=BG,
∴D是AG的中点,
又∵DE∥BG,
∴E是AB的中点,F是AC的中点,
∴DE是△ABG的中位线,EF是△ABC的中位线,
∴EF=BC=2,
又∵EF=2DF,
∴DF=1,
∴DE=3,
∴BG=2DE=6,
∴AB=6,
故选:B.
6.解:∵AB=AC,ED=EA,∠A=36°,
∴∠ABC=∠C=72°,∠ADE=36°,△ABC是等腰三角形,△ADE是等腰三角形,
∵BD平分∠ABC,
∴∠CBD=∠DBA=36°=∠A,
∴∠CDB=72°,DB=DA,即△ABD是等腰三角形,
∴∠C=∠CDB,
∴BC=BD,即△BCD是等腰三角形,
∵DF∥BC,
∴∠AFD=∠ADF=∠C=72°,∠BDF=∠DBC=∠DBF=36°,
∴AF=AD,即△ADF是等腰三角形,
BF=DF,即△BDF是等腰三角形,
∵∠FED=∠A+∠ADE=72°=∠AFD,
∴BE=BD,即△BDE是等腰三角形,
∵∠FED=∠EFD=72°,
∴DF=DE,即△DEF是等腰三角形,
故图中等腰三角形有8个,
故选:C.
7.解:∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∵BI平分∠ABC,CI平分∠ACB,
∴∠IBC=∠ABC=30°,∠ICB=∠ACB=30°,
∴∠BIC=180°﹣30°﹣30°=120°,
故选:C.
8.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
9.解:当2是腰时,2,2,3能组成三角形,
周长=3+2+2=7(cm);
当3是腰时,3,3,2能够组成三角形,
周长=3+3+2=8(cm),
综上所述,周长为7cm或8cm,
故答案为:7cm或8cm.
10.解:∵AD是BC边上的高,CE是AB边上的高,
∴AB CE=BC AD,
∵AD=6,CE=8,
∵AB=AC,AD⊥BC,
∴BD=DC=BC,
∵AB2﹣BD2=AD2,
∴AB2=BC2+36,即BC2=BC2+36,
解得:BC=.
故答案为:.
11.解:设顶角为x度,则
当底角为x°﹣45°时,2(x°﹣45°)+x°=180°,
解得x=90°,
当底角为x°+45°时,2(x°+45°)+x°=180°,
解得x=30°,
∴顶角度数为90°或30°.
故答案为:90°或30°.
12.解:①当AB=AC时,
∵∠B=50°,
∴∠C=∠B=50°.
②当CA=CB时,
∵∠A=∠B=50°,
∴∠C=80°.
③当BA=BC时,
∴∠C=∠A==65°,
综上所述,∠C的值为50°或80°或65°,
故答案为:50°或80°或65°.
13.解:①当BP=PQ时,如图1,
由题意得:BP=PQ=AQ=t,
Rt△ABC中,AC=3,BC=4,
∴AB=5,
∴AP=5﹣t,
过Q作QD⊥AB于D,
∴AD=AP=,
∵∠A=∠A,∠ADQ=∠ACB=90°,
∴△ADQ∽△ACB,
∴t=;
②当BP=BQ时,如图2
由题意得:BP=AC+CQ=t,
∴BQ=3+4﹣t=7﹣t,
∴7﹣t=t,
t=;
③当BQ=PQ时,如图3,
过Q作QD⊥AB于D,
∴BD=BP=t,BQ=7﹣t,
∵∠B=∠B,∠BDQ=∠ACB=90°,
∴t=,
综上所述,t的值是秒或秒或秒.
故答案为:秒或秒或秒.
14.解:如图所示,在BD取点E,使得ED=CD=3,连接AE,则AD垂直平分CE,
∴AE=AC=5,
∴∠AED=∠C=2∠B,
又∵∠AED=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=5,
∴BC=BE+ED+CD=5+3+3=11.
故答案为:11.
15.解:∵等边△ABC
∴∠A=∠ABC=∠ACB=60°,AC=BC
∵∠ABE:∠CBE=1:2
∴∠CBE=∠ABC=40°
又∵AD=CE
∴△ADC≌△CEB(SAS)
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°.
故答案为100°.
16.解:∵在△ABC中,AB=AC,∠A=60°,
∴△ABC是等边三角形,
∵△ABC的周长是24,
∴AB=AC=BC=8,
∵BE⊥AC于E,
∴CE=AC=4,∠EBC=∠ABC=30°,
∴BE=a=4,
∵CD=CE,
∴∠D=∠CED,
∵∠ACB是△CDE的一个外角,
∴∠D+∠CED=∠ACB=60°
∴∠D=30°,
∴∠D=∠EBC,
∴BE=DE=a=4,
∴△BED周长是DE+BE+BD=a+a+(8+4)=2a+12=8+12.
故答案为:8+12.
三.解答题(共4小题)
17.解:(1)设底边长为xcm,则腰长为2xcm.
依题意,得2x+2x+x=18,
解得x=.
∴2x=.
∴三角形三边的长为cm、cm、cm.
(2)若腰长为4cm,则底边长为18﹣4﹣4=10cm.
而4+4<10,所以不能围成腰长为4cm的等腰三角形.
若底边长为4cm,则腰长为(18﹣4)=7cm.
此时能围成等腰三角形,三边长分别为4cm、7cm、7cm.
18.解:(1)∵BD平分∠ABC,ED∥BC,
∴∠EBD=∠CBD,∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE,即△BDE是等腰三角形.
(2)∵OB平分∠ABC,
∴∠CBO=∠ABO,
∵EF∥BC,
∴∠BOE=∠CBO,
∴∠ABO=∠BOE,
∴BE=OE,
同理可得CF=OF,
∵EF=EO+OF,
∴EF=BE+CF.
19.解:(1)∵BD是等边△ABC的中线,
∴BD⊥AC,BD平分AC,
∵AB=6,
∴AD=3,
∴由勾股定理得,BD==3;
(2)证明∵BD是等边△ABC的中线,
∴BD平分∠ABC,
∴∠DBE=∠ABC=30°,
又∵CE=CD,
∴∠E=∠CDE,∠E=∠ACB=30°.
∴∠DBE=∠E,
∴DB=DE.
∵DF⊥BE,
∴DF为底边上的中线.
∴BF=EF;
(3)∵AD=CD,CE=CD,
∴CE=CD=3,
∴BE=BC+CE=9,
∵∠DBE=30°,DB=3,
∴DF=DB=×3=,
∴△BDE的面积=BE DF=×9×=.
20.解:(1)BE垂直平分AD,理由:
∵AM⊥BC,
∴∠ABC+∠5=90°,
∵∠BAC=90°,
∴∠ABC+∠C=90°,
∴∠5=∠C;
∵AD平分∠MAC,
∴∠3=∠4,
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∠5=∠C,
∴∠BAD=∠ADB,
∴△BAD是等腰三角形,
又∵∠1=∠2,
∴BE垂直平分AD.
(2)△ABD、△GAE是等边三角形.理由:
∵BE垂直平分AD,
∴BA=BD,
又∵∠C=30°,∠BAC=90°,
∴∠ABD=60°,
∴△ABD是等边三角形.
∵Rt△BGM中,∠BGM=60°=∠AGE,
又∵Rt△ACM中,∠CAM=60°,
∴∠AEG=∠AGE=∠GAE,
∴△AEG是等边三角形.
一.选择题
1.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
2.等腰三角形的一个内角是68°,则顶角是( )
A.68° B.44° C.68°或44° D.68°或112°
3.如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN或直线PQ上找一点C,使△ABC是等腰三角形,则这样的C点有( )
A.3个 B.4个 C.7个 D.8个
4.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
5.如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分别交AB、AC于点E、F,若EF=2DF,则AB的长为( )
A.4 B.6 C.8 D.10
6.如图,已知△ABC中,AB=AC,∠A=36°;BD平分∠ABC交AC于点D,点E是边AB上的一点,且满足ED=EA;过点D作DF∥CB交AB于点F,则图中等腰三角形的个数为( )
A.6个 B.7个 C.8个 D.9个
7.等边△ABC的两条角平分线BD和CE交于点I,则∠BIC的度数是( )
A.60° B.115° C.120° D.130°
8.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
二.填空题
9.如果等腰三角形有两条边长分别为2cm和3cm,那么它的周长是 .
10.如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,则BC= cm
11.如果等腰三角形的两内角度数相差45°,那么它的顶角度数为 .
12.△ABC中,∠B=50°,当∠C= 时,△ABC是等腰三角形.
13.如图,在△ABC中,∠C=90°,AC=3,BC=4,动点P从点B出发以每秒1个单位长度的速度沿B→A匀速运动;同时点Q从点A出发同样的速度沿A→C→B匀速运动.当点P到达点A时,P、Q同时停止运动,设运动时间为t秒,当t为 时,以B、P、Q为顶点的三角形是等腰三角形.
14.如图,∠C=2∠B,AD⊥BC,AC=5,CD=3,则BC= .
15.如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP= 度.
16.如图,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是 .
三.解答题
17.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长.
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
18.(1)如图①,在△ABC中,BD平分∠ABC,过点D作ED∥BC.指出图中的等腰三角形,并说明理由.
(2)如图②,在△ABC中,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC.证明:EF=BE+CF.
19.如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF;
(3)求△BDE的面积.
20.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.
参考答案
1.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
2.解:若顶角是68°,则结论显然;
若底角是68°,则顶角=180°﹣68°×2=44°.
故选:C.
3.解:使△ABC是等腰三角形,
当AB当底时,则作AB的垂直平分线,交PQ,MN的有两点,即有两个三角形.
当让AB当腰时,则以点A为圆心,AB为半径画圆交PQ,MN有三点,所以有三个.
当以点B为圆心,AB为半径画圆,交PQ,MN有三点,所以有三个.
所以共8个.
故选:D.
4.解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
5.解:如图,延长AD,BC交于点G,
∵BD平分∠ABC,
∴∠ABD=∠GBD,
∵AD⊥BD于点D,
∴∠ADB=∠GDB=90°,
又∵BD=BD,
∴△ABD≌△GBD(ASA),
∴AB=BG,
∴D是AG的中点,
又∵DE∥BG,
∴E是AB的中点,F是AC的中点,
∴DE是△ABG的中位线,EF是△ABC的中位线,
∴EF=BC=2,
又∵EF=2DF,
∴DF=1,
∴DE=3,
∴BG=2DE=6,
∴AB=6,
故选:B.
6.解:∵AB=AC,ED=EA,∠A=36°,
∴∠ABC=∠C=72°,∠ADE=36°,△ABC是等腰三角形,△ADE是等腰三角形,
∵BD平分∠ABC,
∴∠CBD=∠DBA=36°=∠A,
∴∠CDB=72°,DB=DA,即△ABD是等腰三角形,
∴∠C=∠CDB,
∴BC=BD,即△BCD是等腰三角形,
∵DF∥BC,
∴∠AFD=∠ADF=∠C=72°,∠BDF=∠DBC=∠DBF=36°,
∴AF=AD,即△ADF是等腰三角形,
BF=DF,即△BDF是等腰三角形,
∵∠FED=∠A+∠ADE=72°=∠AFD,
∴BE=BD,即△BDE是等腰三角形,
∵∠FED=∠EFD=72°,
∴DF=DE,即△DEF是等腰三角形,
故图中等腰三角形有8个,
故选:C.
7.解:∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∵BI平分∠ABC,CI平分∠ACB,
∴∠IBC=∠ABC=30°,∠ICB=∠ACB=30°,
∴∠BIC=180°﹣30°﹣30°=120°,
故选:C.
8.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
9.解:当2是腰时,2,2,3能组成三角形,
周长=3+2+2=7(cm);
当3是腰时,3,3,2能够组成三角形,
周长=3+3+2=8(cm),
综上所述,周长为7cm或8cm,
故答案为:7cm或8cm.
10.解:∵AD是BC边上的高,CE是AB边上的高,
∴AB CE=BC AD,
∵AD=6,CE=8,
∵AB=AC,AD⊥BC,
∴BD=DC=BC,
∵AB2﹣BD2=AD2,
∴AB2=BC2+36,即BC2=BC2+36,
解得:BC=.
故答案为:.
11.解:设顶角为x度,则
当底角为x°﹣45°时,2(x°﹣45°)+x°=180°,
解得x=90°,
当底角为x°+45°时,2(x°+45°)+x°=180°,
解得x=30°,
∴顶角度数为90°或30°.
故答案为:90°或30°.
12.解:①当AB=AC时,
∵∠B=50°,
∴∠C=∠B=50°.
②当CA=CB时,
∵∠A=∠B=50°,
∴∠C=80°.
③当BA=BC时,
∴∠C=∠A==65°,
综上所述,∠C的值为50°或80°或65°,
故答案为:50°或80°或65°.
13.解:①当BP=PQ时,如图1,
由题意得:BP=PQ=AQ=t,
Rt△ABC中,AC=3,BC=4,
∴AB=5,
∴AP=5﹣t,
过Q作QD⊥AB于D,
∴AD=AP=,
∵∠A=∠A,∠ADQ=∠ACB=90°,
∴△ADQ∽△ACB,
∴t=;
②当BP=BQ时,如图2
由题意得:BP=AC+CQ=t,
∴BQ=3+4﹣t=7﹣t,
∴7﹣t=t,
t=;
③当BQ=PQ时,如图3,
过Q作QD⊥AB于D,
∴BD=BP=t,BQ=7﹣t,
∵∠B=∠B,∠BDQ=∠ACB=90°,
∴t=,
综上所述,t的值是秒或秒或秒.
故答案为:秒或秒或秒.
14.解:如图所示,在BD取点E,使得ED=CD=3,连接AE,则AD垂直平分CE,
∴AE=AC=5,
∴∠AED=∠C=2∠B,
又∵∠AED=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=5,
∴BC=BE+ED+CD=5+3+3=11.
故答案为:11.
15.解:∵等边△ABC
∴∠A=∠ABC=∠ACB=60°,AC=BC
∵∠ABE:∠CBE=1:2
∴∠CBE=∠ABC=40°
又∵AD=CE
∴△ADC≌△CEB(SAS)
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°.
故答案为100°.
16.解:∵在△ABC中,AB=AC,∠A=60°,
∴△ABC是等边三角形,
∵△ABC的周长是24,
∴AB=AC=BC=8,
∵BE⊥AC于E,
∴CE=AC=4,∠EBC=∠ABC=30°,
∴BE=a=4,
∵CD=CE,
∴∠D=∠CED,
∵∠ACB是△CDE的一个外角,
∴∠D+∠CED=∠ACB=60°
∴∠D=30°,
∴∠D=∠EBC,
∴BE=DE=a=4,
∴△BED周长是DE+BE+BD=a+a+(8+4)=2a+12=8+12.
故答案为:8+12.
三.解答题(共4小题)
17.解:(1)设底边长为xcm,则腰长为2xcm.
依题意,得2x+2x+x=18,
解得x=.
∴2x=.
∴三角形三边的长为cm、cm、cm.
(2)若腰长为4cm,则底边长为18﹣4﹣4=10cm.
而4+4<10,所以不能围成腰长为4cm的等腰三角形.
若底边长为4cm,则腰长为(18﹣4)=7cm.
此时能围成等腰三角形,三边长分别为4cm、7cm、7cm.
18.解:(1)∵BD平分∠ABC,ED∥BC,
∴∠EBD=∠CBD,∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE,即△BDE是等腰三角形.
(2)∵OB平分∠ABC,
∴∠CBO=∠ABO,
∵EF∥BC,
∴∠BOE=∠CBO,
∴∠ABO=∠BOE,
∴BE=OE,
同理可得CF=OF,
∵EF=EO+OF,
∴EF=BE+CF.
19.解:(1)∵BD是等边△ABC的中线,
∴BD⊥AC,BD平分AC,
∵AB=6,
∴AD=3,
∴由勾股定理得,BD==3;
(2)证明∵BD是等边△ABC的中线,
∴BD平分∠ABC,
∴∠DBE=∠ABC=30°,
又∵CE=CD,
∴∠E=∠CDE,∠E=∠ACB=30°.
∴∠DBE=∠E,
∴DB=DE.
∵DF⊥BE,
∴DF为底边上的中线.
∴BF=EF;
(3)∵AD=CD,CE=CD,
∴CE=CD=3,
∴BE=BC+CE=9,
∵∠DBE=30°,DB=3,
∴DF=DB=×3=,
∴△BDE的面积=BE DF=×9×=.
20.解:(1)BE垂直平分AD,理由:
∵AM⊥BC,
∴∠ABC+∠5=90°,
∵∠BAC=90°,
∴∠ABC+∠C=90°,
∴∠5=∠C;
∵AD平分∠MAC,
∴∠3=∠4,
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∠5=∠C,
∴∠BAD=∠ADB,
∴△BAD是等腰三角形,
又∵∠1=∠2,
∴BE垂直平分AD.
(2)△ABD、△GAE是等边三角形.理由:
∵BE垂直平分AD,
∴BA=BD,
又∵∠C=30°,∠BAC=90°,
∴∠ABD=60°,
∴△ABD是等边三角形.
∵Rt△BGM中,∠BGM=60°=∠AGE,
又∵Rt△ACM中,∠CAM=60°,
∴∠AEG=∠AGE=∠GAE,
∴△AEG是等边三角形.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
