2021-2022学年苏科版数学八年级上册2.2轴对称的性质课件(31张)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册2.2轴对称的性质课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 10:54:12 | ||
图片预览




文档简介
(共31张PPT)
探索轴对称的性质
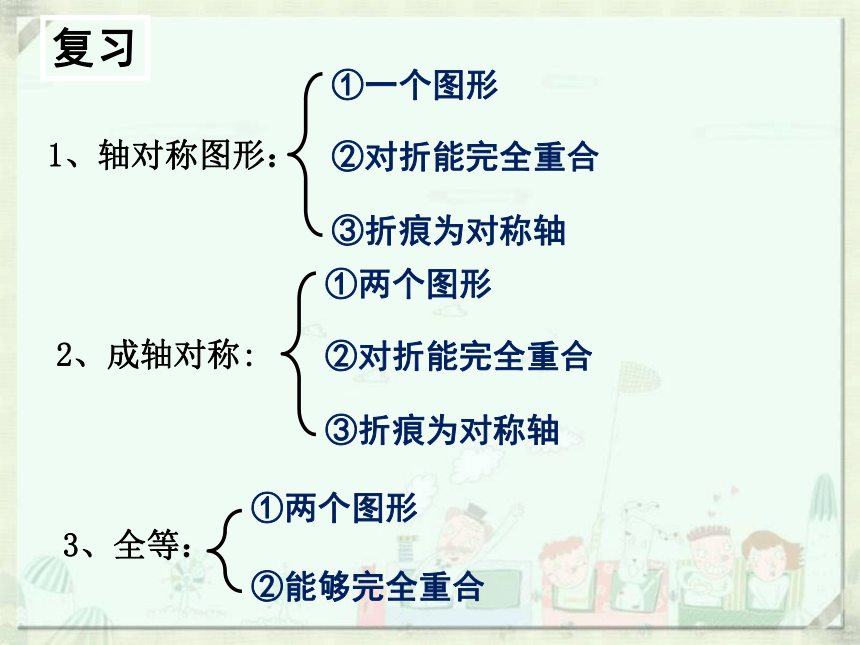
复习
1、轴对称图形:
①一个图形
②对折能完全重合
③折痕为对称轴
2、成轴对称:
①两个图形
②对折能完全重合
③折痕为对称轴
3、全等:
①两个图形
②能够完全重合
图片欣赏
引入
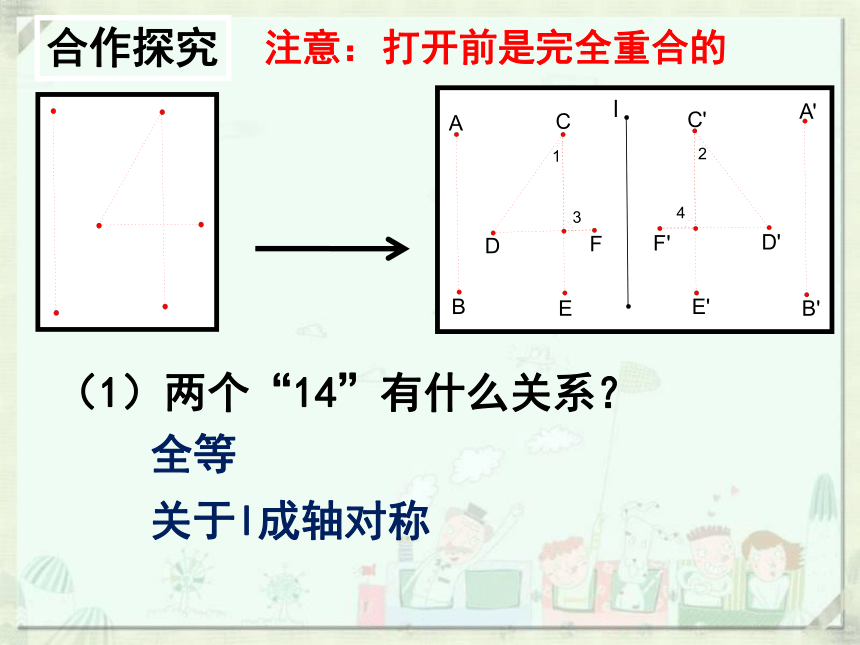
实验操作:将一张长方形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
(1)两个“14”有什么关系?
注意:
打开前是完全重合的
关于l成轴对称
l
全等
合作探究
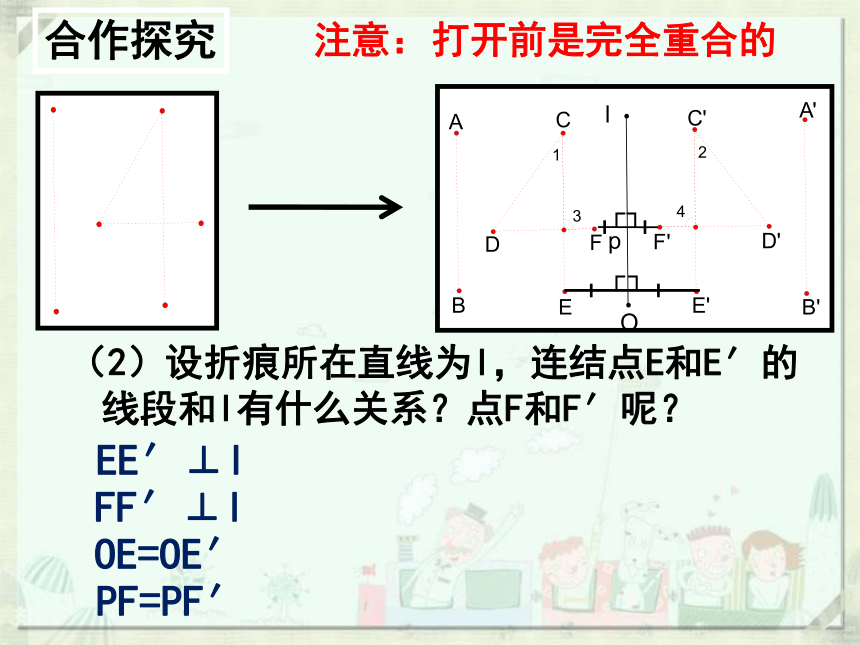
(2)设折痕所在直线为l,连结点E和E′的线段和l有什么关系?点F和F′呢?
┐
┌
O
┐
┌
p
l
EE′⊥l
FF′⊥l
OE=OE′
PF=PF′
注意:
打开前是完全重合的
合作探究
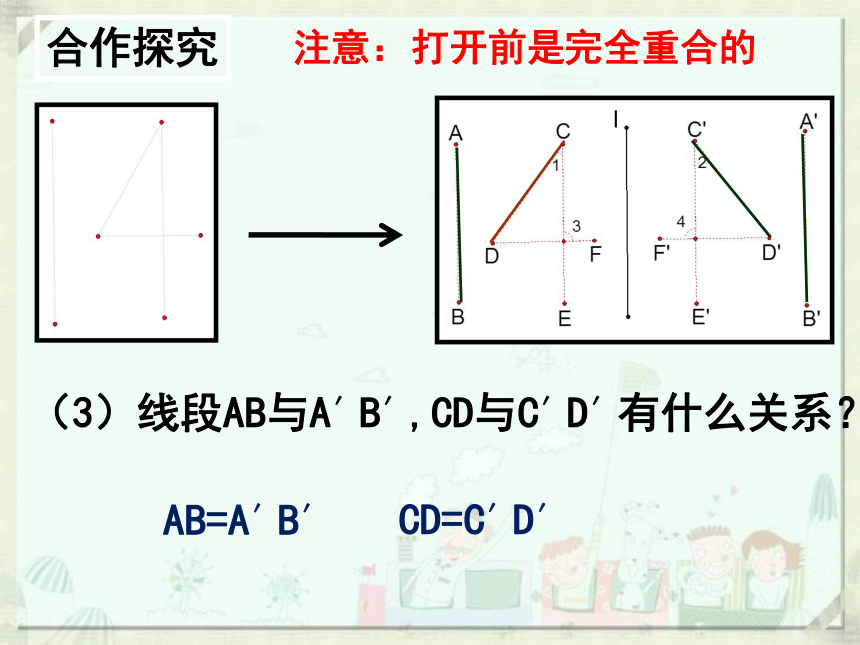
(3)线段AB与A′B′,CD与C′D′有什么关系?
l
AB=A′B′
CD=C′D′
注意:
打开前是完全重合的
合作探究
(4)∠1与∠2有什么关系?∠3与∠4呢?
l
∠1=∠2
∠3=∠4
注意:
打开前是完全重合的
合作探究
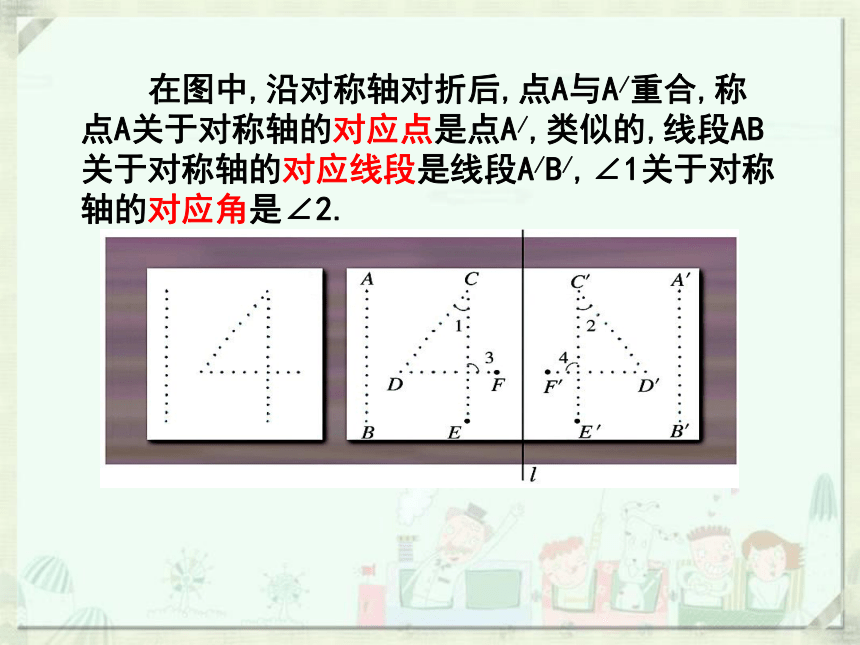
在图中,沿对称轴对折后,点A与A/重合,称点A关于对称轴的对应点是点A/,类似的,线段AB关于对称轴的对应线段是线段A/B/,∠1关于对称轴的对应角是∠2.
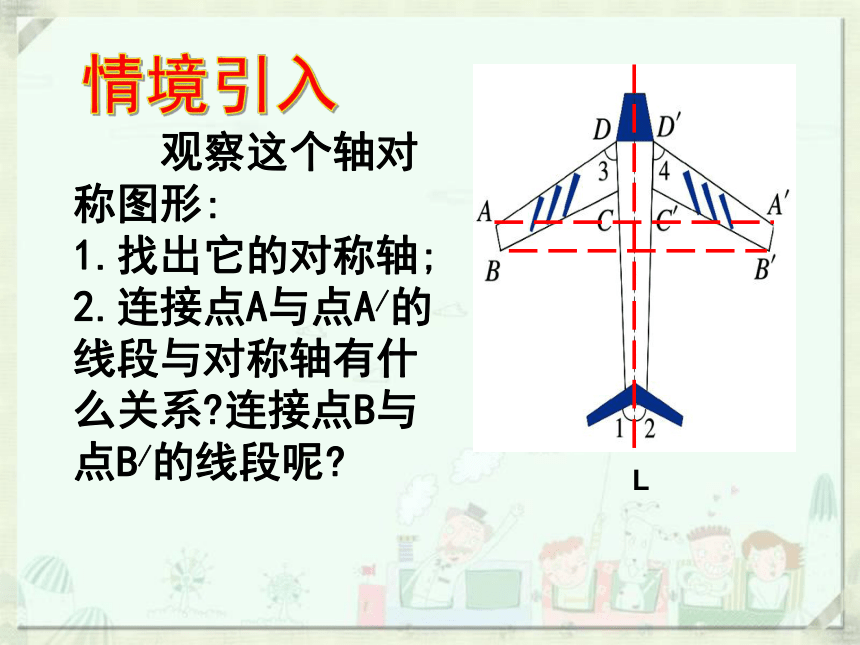
观察这个轴对称图形:
1.找出它的对称轴;
2.连接点A与点A/的线段与对称轴有什么关系 连接点B与点B/的线段呢
L
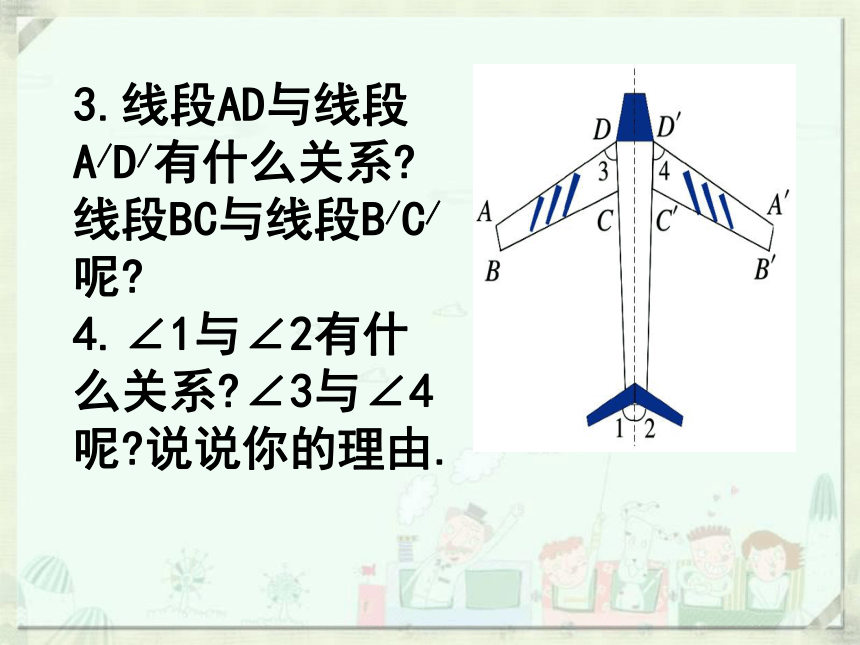
3.线段AD与线段 A/D/有什么关系 线段BC与线段B/C/呢
4.∠1与∠2有什么关系 ∠3与∠4呢 说说你的理由.
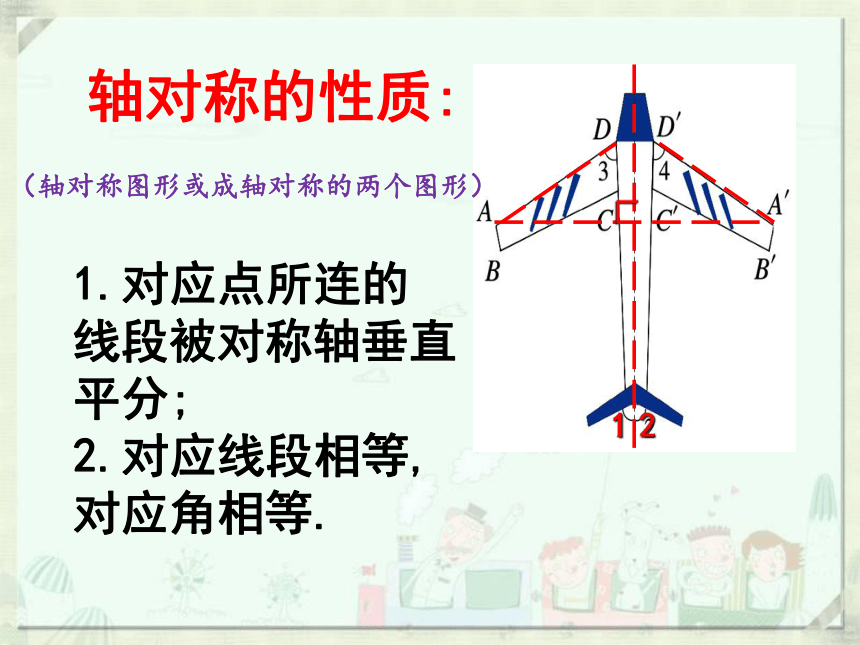
轴对称的性质:
1.对应点所连的线段被对称轴垂直平分;
2.对应线段相等,对应角相等.
∟
1
2
(轴对称图形或成轴对称的两个图形)
图中给出了一个图案的一半,其中的虚线是这个图案的对称轴.
1.你能猜出整个图案的形状吗?
2.你能画出这个图案的另一半吗?
已知对称轴l和一个点A,要画出点A关于l的对应点A/.
A
A
∟
l
过点A作对称轴l的垂线,垂足为B,延长AB至A/, 使得BA/=AB.点A/就是点A关于直线l的对应点。
B
A/
A
A/
B
B/
利用轴对称性质作图:
把关键的点先确定好
作图
判断:
①设A、B关于直线MN对称,则AB垂直平分MN。( )
②如果△ABC≌△DEF,则一定存在一条直线MN,使△ABC与△DEF关于MN对称。( )
③如果一个三角形是轴对称图形,且对称轴不止一条,则它是等边三角形。( )
④两个图形关于MN对称,则这两个图形分别在MN的两侧。( )
╳
╳
╳
√
练习
1.如图⊿ABC和⊿A/B/C/关于直线l对称, A/B/=6cm,∠ABC=90°,则∠ A/B/C/ =____°, AB=___cm.
A
A/
B
B/
C
C/
l
90
6
2. 如图,△ABC与△DEF关于直线L成轴对称。
①请写出其中相等的线段;
②如果△ABC的面积为6cm2,且DE=3cm,求△ABC中AB边上的高h。
L
C
A
B
E
F
D
3.下列说法中正确的是 ( )
A.轴对称图形的对应点所连线段垂直平分对称轴;
B.轴对称图形上若有一点在对称轴上,则该点与它的对应点重合;
C.轴对称图形的对应点一定在对称轴两侧;
D.两个全等的图形一定成轴对称.
B
4.如图,⊿ABC和⊿A/B/C/关于直线l对称,这两个三角形全等吗 如果⊿ABC≌⊿A/B/C/,那么⊿ABC和⊿A/B/C/一定关于直线l对称吗
l
A
A/
B
B/
C
C/
A
A/
B
B/
C
C/
答:如果⊿ABC和⊿A/B/C/关于直线l对称,那么这两个三角形全等;如果⊿ABC≌⊿A/B/C/,那么⊿ABC和⊿A/B/C/不一定关于直线l对称。
l
A
A/
B
B/
C
C/
如图,已知点A、B直线MN同侧两点,点A1、A关于直线MN对称。连接A1B交直线MN于点P,连接AP。
(1)若A1B=5cm,则AP+BP的长为
5cm
能力拓展
A
B
P
A1
N
M
(2)若P1为直线MN上任意一点(不与P重合),连结AP1、BP1,试说明 AP1+BP1 AP+BP。
A1
A
B
P
N
M
P1
1.如图,在一条河的两侧有A、B两个村庄,要在河边修建码头M,使M到A、B两个村庄的距离之和最短,试确定M的位置。
l
A
B
M
2.如图,在一条河的同一岸边有A、B两个村庄,要在河边修建码头M,使M到A、B两个村庄的距离之和最短,试确定M的位置。
l
A
B
M
A/
3.如图,D、E分别是⊿ABC的边AB和边AC上的两点,在BC上求作一点F,使⊿DEF的周长最小。
A
B
D
C
E
F
D/
4.如图,小虎住在甲村,姥姥住在乙村,星期天小虎去看姥姥,先在北山坡打一捆草,又在南山坡砍一捆柴,然后给姥姥送去。问小虎应选择怎样的路线才最短?
北山坡
南山坡
乙村
甲村
A
B
C
D
我来小结
本节知识梳理
实例探索
轴对称性质
对应线段相等
对应角相等
观察
发现
对应点所连线段被对称轴垂直平分
—
—
—
探索轴对称的性质
复习
1、轴对称图形:
①一个图形
②对折能完全重合
③折痕为对称轴
2、成轴对称:
①两个图形
②对折能完全重合
③折痕为对称轴
3、全等:
①两个图形
②能够完全重合
图片欣赏
引入
实验操作:将一张长方形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
(1)两个“14”有什么关系?
注意:
打开前是完全重合的
关于l成轴对称
l
全等
合作探究
(2)设折痕所在直线为l,连结点E和E′的线段和l有什么关系?点F和F′呢?
┐
┌
O
┐
┌
p
l
EE′⊥l
FF′⊥l
OE=OE′
PF=PF′
注意:
打开前是完全重合的
合作探究
(3)线段AB与A′B′,CD与C′D′有什么关系?
l
AB=A′B′
CD=C′D′
注意:
打开前是完全重合的
合作探究
(4)∠1与∠2有什么关系?∠3与∠4呢?
l
∠1=∠2
∠3=∠4
注意:
打开前是完全重合的
合作探究
在图中,沿对称轴对折后,点A与A/重合,称点A关于对称轴的对应点是点A/,类似的,线段AB关于对称轴的对应线段是线段A/B/,∠1关于对称轴的对应角是∠2.
观察这个轴对称图形:
1.找出它的对称轴;
2.连接点A与点A/的线段与对称轴有什么关系 连接点B与点B/的线段呢
L
3.线段AD与线段 A/D/有什么关系 线段BC与线段B/C/呢
4.∠1与∠2有什么关系 ∠3与∠4呢 说说你的理由.
轴对称的性质:
1.对应点所连的线段被对称轴垂直平分;
2.对应线段相等,对应角相等.
∟
1
2
(轴对称图形或成轴对称的两个图形)
图中给出了一个图案的一半,其中的虚线是这个图案的对称轴.
1.你能猜出整个图案的形状吗?
2.你能画出这个图案的另一半吗?
已知对称轴l和一个点A,要画出点A关于l的对应点A/.
A
A
∟
l
过点A作对称轴l的垂线,垂足为B,延长AB至A/, 使得BA/=AB.点A/就是点A关于直线l的对应点。
B
A/
A
A/
B
B/
利用轴对称性质作图:
把关键的点先确定好
作图
判断:
①设A、B关于直线MN对称,则AB垂直平分MN。( )
②如果△ABC≌△DEF,则一定存在一条直线MN,使△ABC与△DEF关于MN对称。( )
③如果一个三角形是轴对称图形,且对称轴不止一条,则它是等边三角形。( )
④两个图形关于MN对称,则这两个图形分别在MN的两侧。( )
╳
╳
╳
√
练习
1.如图⊿ABC和⊿A/B/C/关于直线l对称, A/B/=6cm,∠ABC=90°,则∠ A/B/C/ =____°, AB=___cm.
A
A/
B
B/
C
C/
l
90
6
2. 如图,△ABC与△DEF关于直线L成轴对称。
①请写出其中相等的线段;
②如果△ABC的面积为6cm2,且DE=3cm,求△ABC中AB边上的高h。
L
C
A
B
E
F
D
3.下列说法中正确的是 ( )
A.轴对称图形的对应点所连线段垂直平分对称轴;
B.轴对称图形上若有一点在对称轴上,则该点与它的对应点重合;
C.轴对称图形的对应点一定在对称轴两侧;
D.两个全等的图形一定成轴对称.
B
4.如图,⊿ABC和⊿A/B/C/关于直线l对称,这两个三角形全等吗 如果⊿ABC≌⊿A/B/C/,那么⊿ABC和⊿A/B/C/一定关于直线l对称吗
l
A
A/
B
B/
C
C/
A
A/
B
B/
C
C/
答:如果⊿ABC和⊿A/B/C/关于直线l对称,那么这两个三角形全等;如果⊿ABC≌⊿A/B/C/,那么⊿ABC和⊿A/B/C/不一定关于直线l对称。
l
A
A/
B
B/
C
C/
如图,已知点A、B直线MN同侧两点,点A1、A关于直线MN对称。连接A1B交直线MN于点P,连接AP。
(1)若A1B=5cm,则AP+BP的长为
5cm
能力拓展
A
B
P
A1
N
M
(2)若P1为直线MN上任意一点(不与P重合),连结AP1、BP1,试说明 AP1+BP1 AP+BP。
A1
A
B
P
N
M
P1
1.如图,在一条河的两侧有A、B两个村庄,要在河边修建码头M,使M到A、B两个村庄的距离之和最短,试确定M的位置。
l
A
B
M
2.如图,在一条河的同一岸边有A、B两个村庄,要在河边修建码头M,使M到A、B两个村庄的距离之和最短,试确定M的位置。
l
A
B
M
A/
3.如图,D、E分别是⊿ABC的边AB和边AC上的两点,在BC上求作一点F,使⊿DEF的周长最小。
A
B
D
C
E
F
D/
4.如图,小虎住在甲村,姥姥住在乙村,星期天小虎去看姥姥,先在北山坡打一捆草,又在南山坡砍一捆柴,然后给姥姥送去。问小虎应选择怎样的路线才最短?
北山坡
南山坡
乙村
甲村
A
B
C
D
我来小结
本节知识梳理
实例探索
轴对称性质
对应线段相等
对应角相等
观察
发现
对应点所连线段被对称轴垂直平分
—
—
—
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
