2021—2022学年人教版数学八年级上册13.1.2线段的垂直平分线的性质课件(第2课时 21张)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册13.1.2线段的垂直平分线的性质课件(第2课时 21张) |  | |
| 格式 | zip | ||
| 文件大小 | 792.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 10:57:56 | ||
图片预览







文档简介
(共21张PPT)
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
第2课时 线段垂直平分线的有关作图
人教版八年级数学上册
学习目标
1.能用尺规作已知线段的垂直平分线.(难点)
2.进一步了解尺规作图的一般步骤和作图语言,理解作图的依据.
3.能够运用尺规作图的方法解决简单的作图问题.(重点)
温故知新
1.轴对称的性质:
2.线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等。
与一条线段两端点距离相等的点,在这条线段的垂直平分线上。
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
导入新课
情境引入
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
讲授新课
线段垂直平分线的画法
一
互动探究
问题1:有时我们感觉一(两)个平面图形是轴对称的,如何验证呢?
A
B
C
A ′
B ′
C ′
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称的.
问题2:不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例1:尺规作图
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
A
B
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
C
D
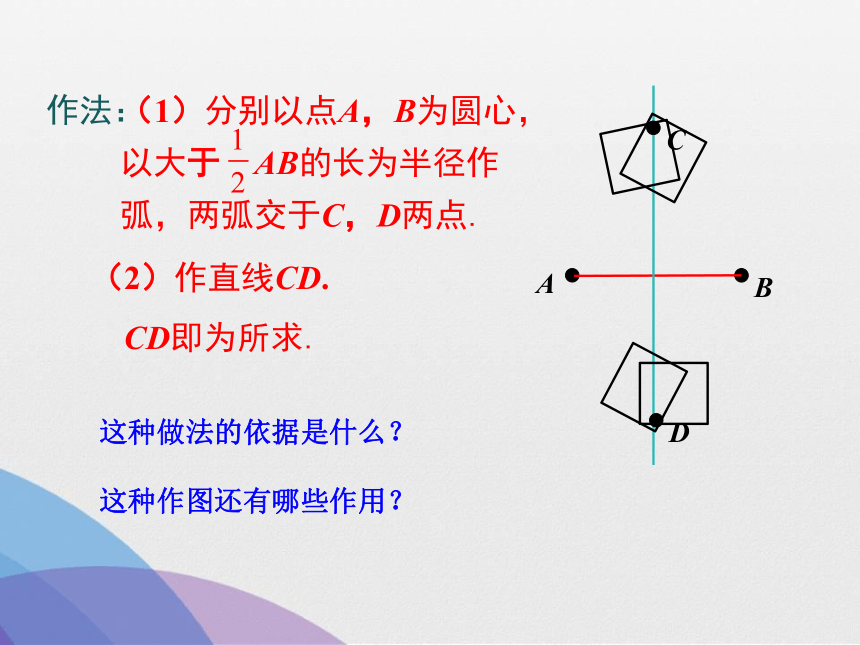
作法:
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
这种做法的依据是什么?
这种作图还有哪些作用?
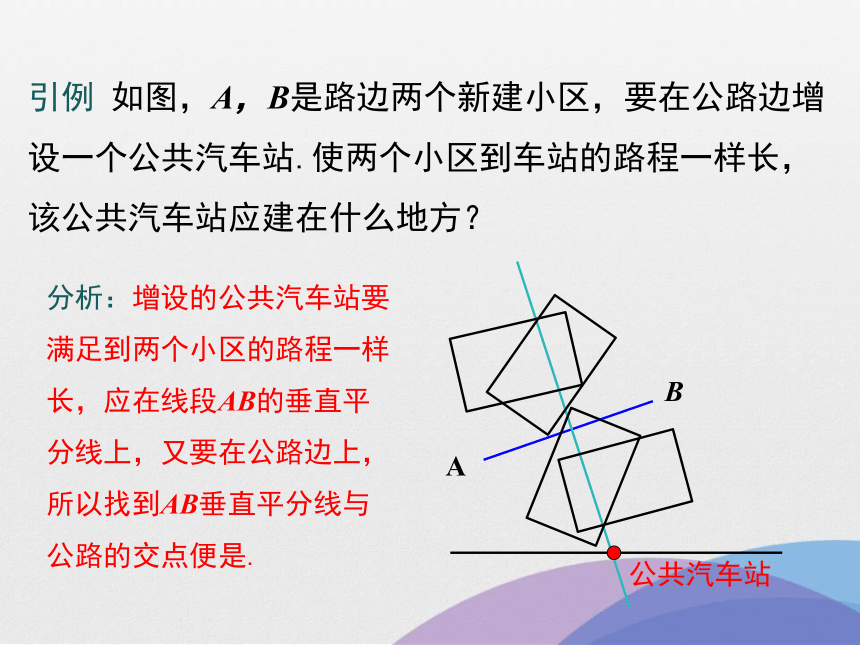
引例 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
公共汽车站
某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)
O
N
M
A
B
典例精析
O
N
M
A
B
方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在两点连线的垂直平分线上.
解:如图所示:
P
二、作轴对称图形的对称轴
如果两个图形成轴对称,怎样做出图形的对称轴?
想一想:下图中的五角星有几条对称轴?如何作出这些对称轴呢?
A
B
作法:(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.则l就是这个五角星的一条对称轴.
l
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
例2
方法总结:
如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线。因此,只要找到任意一对对应点,做出对应点所连线段的垂直平分线,就得到此图形的对称轴。
例3 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
A
B
C
A ′
B ′
C ′
l
方法总结:如果两个图形关于某一条直线对称,且对应线段(或延长线)相交,那么交点必定在对称轴上.
解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
P
Q
练一练:作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?(课本64页第1题)
课堂小结
本节课有哪些收获?
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
反馈矫正
2.如图,与图形A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
3.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
4.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
B
C
学校在连接任意两点的两条线段的垂直平分线的交点处.
A
布置作业
课本习题13.1第10、12题。
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
第2课时 线段垂直平分线的有关作图
人教版八年级数学上册
学习目标
1.能用尺规作已知线段的垂直平分线.(难点)
2.进一步了解尺规作图的一般步骤和作图语言,理解作图的依据.
3.能够运用尺规作图的方法解决简单的作图问题.(重点)
温故知新
1.轴对称的性质:
2.线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等。
与一条线段两端点距离相等的点,在这条线段的垂直平分线上。
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
导入新课
情境引入
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
讲授新课
线段垂直平分线的画法
一
互动探究
问题1:有时我们感觉一(两)个平面图形是轴对称的,如何验证呢?
A
B
C
A ′
B ′
C ′
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称的.
问题2:不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例1:尺规作图
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
A
B
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
这种做法的依据是什么?
这种作图还有哪些作用?
引例 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
公共汽车站
某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)
O
N
M
A
B
典例精析
O
N
M
A
B
方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在两点连线的垂直平分线上.
解:如图所示:
P
二、作轴对称图形的对称轴
如果两个图形成轴对称,怎样做出图形的对称轴?
想一想:下图中的五角星有几条对称轴?如何作出这些对称轴呢?
A
B
作法:(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.则l就是这个五角星的一条对称轴.
l
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
例2
方法总结:
如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线。因此,只要找到任意一对对应点,做出对应点所连线段的垂直平分线,就得到此图形的对称轴。
例3 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
A
B
C
A ′
B ′
C ′
l
方法总结:如果两个图形关于某一条直线对称,且对应线段(或延长线)相交,那么交点必定在对称轴上.
解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
P
Q
练一练:作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?(课本64页第1题)
课堂小结
本节课有哪些收获?
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
反馈矫正
2.如图,与图形A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
3.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
4.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
B
C
学校在连接任意两点的两条线段的垂直平分线的交点处.
A
布置作业
课本习题13.1第10、12题。
