6.3 一次函数的图象 课件(共42张PPT)
文档属性
| 名称 | 6.3 一次函数的图象 课件(共42张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
第六章 一次函数
3 一次函数的图象
知识点一 函数的图象
定义
画法
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
连线
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
连线 按照自变量从小到大的顺序,把所描的点用平滑的线连起来,并按照线的变化趋势延伸
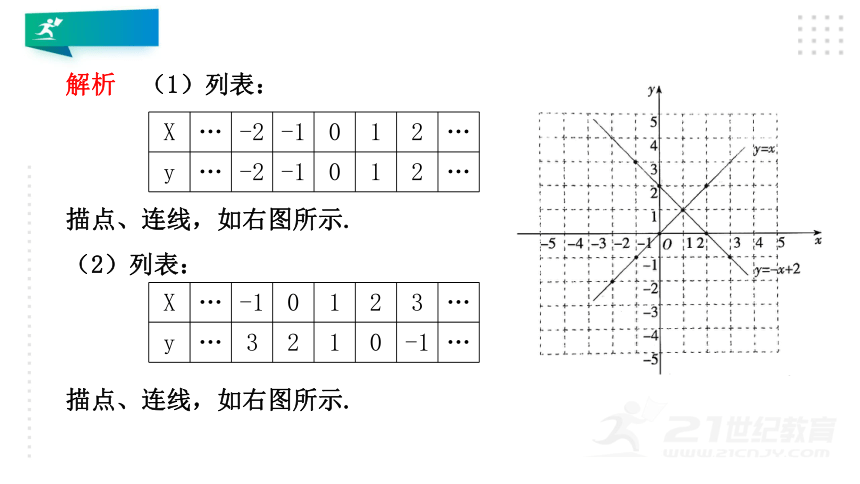
例1 在同一直角坐标系中画出下列函数的图象:
(1)y=x;(2)y=-x+2.
解析 (1)列表:
描点、连线,如右图所示.
(2)列表:
描点、连线,如右图所示.
X … -2 -1 0 1 2 …
y … -2 -1 0 1 2 …
X … -1 0 1 2 3 …
y … 3 2 1 0 -1 …
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点 必过原点(0,0)
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点 必过原点(0,0)
增减性 y的值随x值的增大而增大 y的值随x值的增大而减小
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
解析 对于函数y=kx,因为k>0,所以y随x的增大而增大,故①正确,②错误,当x>0时,y>0,故③正确,④错误.
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
解析 对于函数y=kx,因为k>0,所以y随x的增大而增大,故①正确,②错误,当x>0时,y>0,故③正确,④错误.
答案 ①③
知识点三 一次函数的图象及性质
关系式 y=kx+b(k≠0)
k,b的符号 k>0 k<0
b>0 b<0 b>0 b<0
图象
所过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
图象所过特殊点 经过(0,b)和两点
增减性 y的值随x值的增大而增大 y的值随x值的增大而减小
2.一次函数图象的平移
(1)直线y=kx+b 直线y=kx+b+m.
(2)直线y=hx+b 直线y=kx+b-m.
(3)直线y=kx+b 直线y=k(x+m)+b.
(4)直线y=kx+b 直线y=k(x-m)+b.
总结:上加下减,左加右减.
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
解析 函数y=-2x+2-5,k=-2<0,b=2-5<0,∴该函数的图象是一条直线,故选项A中说法正确;y的值随着x值的增大而减小,故选项B中说法正确;图象经过第二、三、四象限,不经过第一象限,故选项C中说法不正确;图象与y轴的交点坐标为(0,2-5),故选项D中说法正确.
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
解析 函数y=-2x+2-5,k=-2<0,b=2-5<0,∴该函数的图象是一条直线,故选项A中说法正确;y的值随着x值的增大而减小,故选项B中说法正确;图象经过第二、三、四象限,不经过第一象限,故选项C中说法不正确;图象与y轴的交点坐标为(0,2-5),故选项D中说法正确.
答案 C
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
解析 将直线y=向右平移2个单位长度,得直线y=(x-2);再向上平移2个单位长度,所得的直线的解析式是y=(x-2)+2,整理,得y= +1.
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
解析 将直线y=向右平移2个单位长度,得直线y=(x-2);再向上平移2个单位长度,所得的直线的解析式是y=(x-2)+2,整理,得y= +1.
答案 A
经典例题
题型一 一次函数和正比例函数的图象问题
例1 在同一平面直角坐标系中,函数y=kx与y=x-k+2的图象大致为( )
解析 当k>2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、三、四象限,且两图象的交点应位于第三象限;当0<k<2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第一象限;当k<0时,函数y=kx的图象经过第二、四象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第二象限,由上可得,选项A、B、D不符合题意,故选C.
解析 当k>2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、三、四象限,且两图象的交点应位于第三象限;当0<k<2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第一象限;当k<0时,函数y=kx的图象经过第二、四象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第二象限,由上可得,选项A、B、D不符合题意,故选C.
点拨 此类函数图象共存问题,一般根据一次函数的系数与图象的关系依次分析选项,注意在同一题目中k、b取值(或范围)相同的即为正确选项.
题型二 与一次函数图象有关的面积问题
例2 已知一次函数y=kx+b的图象经过点(0,-2),且与两坐标轴围成的三角形的面积为3,求k,b的值.
解析 根据已知条件画出一次函数图象的示意图(如图所示的直线AB或直线A′B).
设直线与x轴的交点坐标为(x,0),则OA=OA′=x,0B=|-2|=2.
因为S△OAB=3,所以0A·0B=3,即|x|·2=3,解得x=±3,
所以A(-3,0),A′(3,0).
因为一次函数y=kx+b的图象经过点(0,-2),所以b=-2.
当x=-3时,-3k-2=0,解得k=;
当x=3时,3k-2=0,解得k=.
综上可知,k= ,b=-2或k= ,b=-2.
点拨
(1)因为一次函数y=kx+b(k≠0)的图象与坐标轴的交点坐标分别为(0,b)和所以一次函数图象与坐标轴围成的三角形的面积为.
(2)在直角坐标系中,利用点的坐标表示线段的长度,当坐标为负数时,要用它的绝对值来表示长度.
易错易混
易错点 忽视函数图象存在的多样性,解题时易漏掉某种情况
正比例函数也是一次函数,一次函数y=kx+b(k≠0且k,b为常数)中的“b”可以等于0,因此,做题时易漏掉“b=0”这一情况.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
解析 当n≠0时,y=mx+n为一次函数,因为图象不经过第一象限,所以m<0,n<0.当n=0时,y=mx+n为正比例函数,
因为图象不经过第一象限,所以m<0,n=0.
综上,m<0,n≤0.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
解析 当n≠0时,y=mx+n为一次函数,因为图象不经过第一象限,所以m<0,n<0.当n=0时,y=mx+n为正比例函数,
因为图象不经过第一象限,所以m<0,n=0.
综上,m<0,n≤0.
易错分析
若图象不经过第一象限,则图象可以经过第二、三、四象限或第二、四象限.不要只考虑到前一种情况,而漏掉第二种情况,从而解出m<0,n<0的错误答案.
第六章 一次函数
3 一次函数的图象
知识点一 函数的图象
定义
画法
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
连线
知识点一 函数的图象
定义 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象
画法 列表 用一个表格给出自变量x与函数值y的一些对应值
描点 以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点
连线 按照自变量从小到大的顺序,把所描的点用平滑的线连起来,并按照线的变化趋势延伸
例1 在同一直角坐标系中画出下列函数的图象:
(1)y=x;(2)y=-x+2.
解析 (1)列表:
描点、连线,如右图所示.
(2)列表:
描点、连线,如右图所示.
X … -2 -1 0 1 2 …
y … -2 -1 0 1 2 …
X … -1 0 1 2 3 …
y … 3 2 1 0 -1 …
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点 必过原点(0,0)
增减性
知识点二 正比例函数的图象及性质
关系式 y=kx(k>0) y=kx(k<0)
图象
所过象限 第一、三象限 第二、四象限
图象所过特殊点 必过原点(0,0)
增减性 y的值随x值的增大而增大 y的值随x值的增大而减小
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
解析 对于函数y=kx,因为k>0,所以y随x的增大而增大,故①正确,②错误,当x>0时,y>0,故③正确,④错误.
例2 若k>0,x>0,则关于函数y=kx的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负数.正确的是_________.(直接写出正确结论的序号)
解析 对于函数y=kx,因为k>0,所以y随x的增大而增大,故①正确,②错误,当x>0时,y>0,故③正确,④错误.
答案 ①③
知识点三 一次函数的图象及性质
关系式 y=kx+b(k≠0)
k,b的符号 k>0 k<0
b>0 b<0 b>0 b<0
图象
所过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
图象所过特殊点 经过(0,b)和两点
增减性 y的值随x值的增大而增大 y的值随x值的增大而减小
2.一次函数图象的平移
(1)直线y=kx+b 直线y=kx+b+m.
(2)直线y=hx+b 直线y=kx+b-m.
(3)直线y=kx+b 直线y=k(x+m)+b.
(4)直线y=kx+b 直线y=k(x-m)+b.
总结:上加下减,左加右减.
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
解析 函数y=-2x+2-5,k=-2<0,b=2-5<0,∴该函数的图象是一条直线,故选项A中说法正确;y的值随着x值的增大而减小,故选项B中说法正确;图象经过第二、三、四象限,不经过第一象限,故选项C中说法不正确;图象与y轴的交点坐标为(0,2-5),故选项D中说法正确.
例3 关于函数y=-2x+2-5,下列说法不正确的是( )
A.图象是一条直线 B.y的值随着x值的增大而减小
C.图象不经过第三象限 D.图象与y轴的交点坐标为(0,2-5)
解析 函数y=-2x+2-5,k=-2<0,b=2-5<0,∴该函数的图象是一条直线,故选项A中说法正确;y的值随着x值的增大而减小,故选项B中说法正确;图象经过第二、三、四象限,不经过第一象限,故选项C中说法不正确;图象与y轴的交点坐标为(0,2-5),故选项D中说法正确.
答案 C
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
解析 将直线y=向右平移2个单位长度,得直线y=(x-2);再向上平移2个单位长度,所得的直线的解析式是y=(x-2)+2,整理,得y= +1.
例4 将直线y=向右平移2个单位长度,再向上平移2个单位长度,所得的直线的解析式是( )
A.y=+1 B.y=+3 C.y=-1 D.y= -3
解析 将直线y=向右平移2个单位长度,得直线y=(x-2);再向上平移2个单位长度,所得的直线的解析式是y=(x-2)+2,整理,得y= +1.
答案 A
经典例题
题型一 一次函数和正比例函数的图象问题
例1 在同一平面直角坐标系中,函数y=kx与y=x-k+2的图象大致为( )
解析 当k>2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、三、四象限,且两图象的交点应位于第三象限;当0<k<2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第一象限;当k<0时,函数y=kx的图象经过第二、四象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第二象限,由上可得,选项A、B、D不符合题意,故选C.
解析 当k>2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、三、四象限,且两图象的交点应位于第三象限;当0<k<2时,函数y=kx的图象经过第一、三象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第一象限;当k<0时,函数y=kx的图象经过第二、四象限且过原点,y=x-k+2的图象经过第一、二、三象限,且两图象的交点应位于第二象限,由上可得,选项A、B、D不符合题意,故选C.
点拨 此类函数图象共存问题,一般根据一次函数的系数与图象的关系依次分析选项,注意在同一题目中k、b取值(或范围)相同的即为正确选项.
题型二 与一次函数图象有关的面积问题
例2 已知一次函数y=kx+b的图象经过点(0,-2),且与两坐标轴围成的三角形的面积为3,求k,b的值.
解析 根据已知条件画出一次函数图象的示意图(如图所示的直线AB或直线A′B).
设直线与x轴的交点坐标为(x,0),则OA=OA′=x,0B=|-2|=2.
因为S△OAB=3,所以0A·0B=3,即|x|·2=3,解得x=±3,
所以A(-3,0),A′(3,0).
因为一次函数y=kx+b的图象经过点(0,-2),所以b=-2.
当x=-3时,-3k-2=0,解得k=;
当x=3时,3k-2=0,解得k=.
综上可知,k= ,b=-2或k= ,b=-2.
点拨
(1)因为一次函数y=kx+b(k≠0)的图象与坐标轴的交点坐标分别为(0,b)和所以一次函数图象与坐标轴围成的三角形的面积为.
(2)在直角坐标系中,利用点的坐标表示线段的长度,当坐标为负数时,要用它的绝对值来表示长度.
易错易混
易错点 忽视函数图象存在的多样性,解题时易漏掉某种情况
正比例函数也是一次函数,一次函数y=kx+b(k≠0且k,b为常数)中的“b”可以等于0,因此,做题时易漏掉“b=0”这一情况.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
解析 当n≠0时,y=mx+n为一次函数,因为图象不经过第一象限,所以m<0,n<0.当n=0时,y=mx+n为正比例函数,
因为图象不经过第一象限,所以m<0,n=0.
综上,m<0,n≤0.
例题 已知一次函数y=mx+n(m≠0)的图象不经过第一象限,求m,n的取值范围.
解析 当n≠0时,y=mx+n为一次函数,因为图象不经过第一象限,所以m<0,n<0.当n=0时,y=mx+n为正比例函数,
因为图象不经过第一象限,所以m<0,n=0.
综上,m<0,n≤0.
易错分析
若图象不经过第一象限,则图象可以经过第二、三、四象限或第二、四象限.不要只考虑到前一种情况,而漏掉第二种情况,从而解出m<0,n<0的错误答案.
