2021-2022学年四川省成都市青羊区高三(上)入学数学试卷(理科)(9月份)(word含答案解析版)
文档属性
| 名称 | 2021-2022学年四川省成都市青羊区高三(上)入学数学试卷(理科)(9月份)(word含答案解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览




文档简介
2021-2022学年四川省成都市青羊区高三(上)入学数学试卷(理科)(9月份)
一、选择题(共12小题,每小题3分,满分36分).
1.已知集合A={x|(x+1)(x﹣3)<0},B={1,2,3},则A∩B=( )
A.{x|﹣1<x<3} B.{x|1≤x≤2} C.{1,2,3} D.{1,2}
2.设i是虚数单位,若复数z满足(1+i)z=2i,则z=( )
A.﹣1+i B.1﹣i C.1+i D.﹣1﹣i
3.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为( )
A. B. C. D.
4.如表是某电器销售公司2021年第一季度各类电器营业收入占比和净利润占比统计表:
空调类 冰箱类 小家电类 其他类
营业收入占比 90.10% 4.98% 3.82% 1.10%
净利润占比 95.80% ﹣0.48% 3.82% 0.86%
下列判断中不正确的是( )
A.该公司2021年第一季度冰箱类电器销售亏损
B.该公司2021年第一季度小家电类电器营业收入和净利润相同
C.该公司2021年第一季度净利润主要由空调类电器销售提供
D.剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低
5.已知p=30.5,q=log95,r=log32,则p,q,r的大小关系为( )
A.q>p>r B.p>r>q C.p>q>r D.r>q>p
6.在区间[﹣2,2]上随机取一个数b,若使直线y=x+b与圆x2+y2=a有交点的概率为,则a=( )
A. B. C.1 D.2
7.2019年7月,中国良渚古城遗址获准列入世界遗产名录.良渚古城遗址是人类早期城市文明的范例,实证了华夏五千年文明史.考古学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(年)的衰变规律满足:(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log23≈1.6,log25≈2.3)
A.3440年 B.4010年 C.4580年 D.5160年
8.设(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,则下列结论正确的是( )
A.a0=﹣16 B.a0+a1+a2+a3+a4=81
C.a1+a2+a3+a4=15 D.a0+a2+a4=41
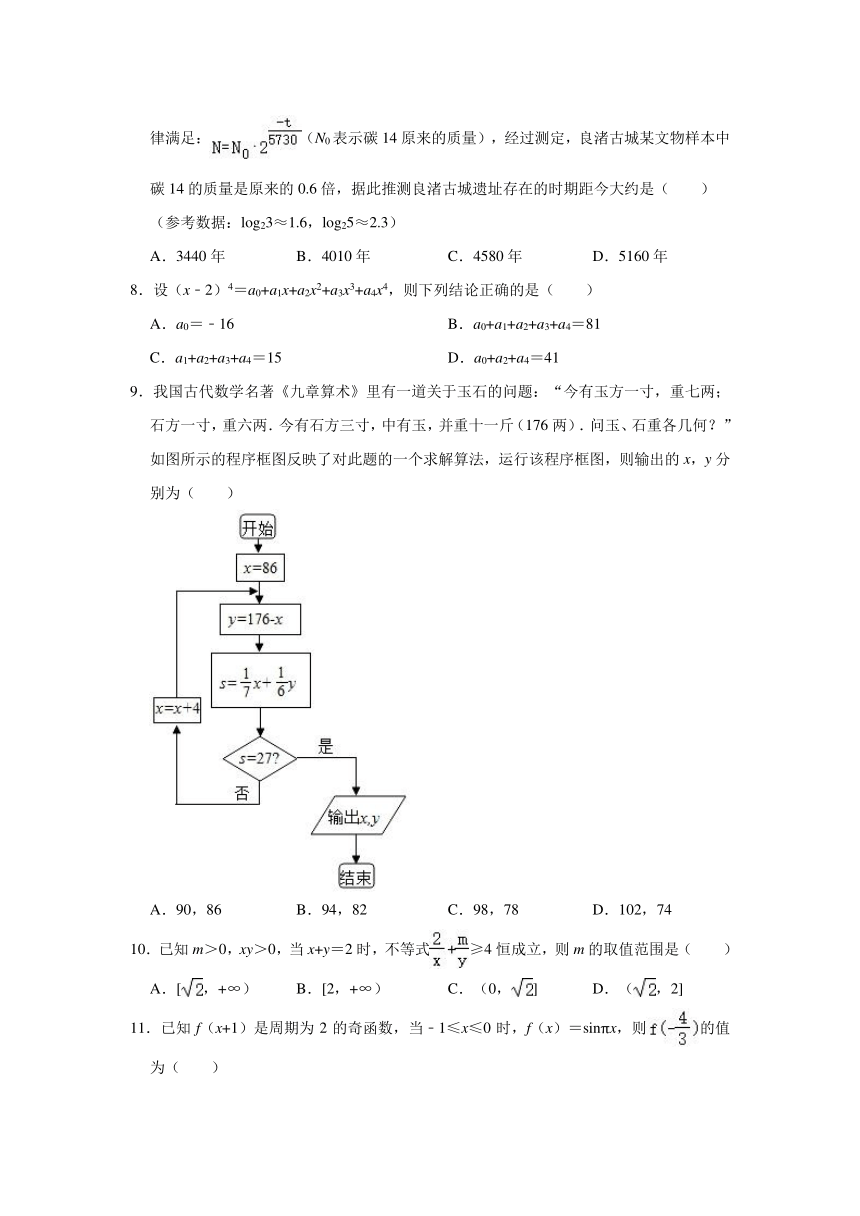
9.我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的x,y分别为( )
A.90,86 B.94,82 C.98,78 D.102,74
10.已知m>0,xy>0,当x+y=2时,不等式≥4恒成立,则m的取值范围是( )
A.[,+∞) B.[2,+∞) C.(0,] D.(,2]
11.已知f(x+1)是周期为2的奇函数,当﹣1≤x≤0时,f(x)=sinπx,则的值为( )
A. B. C. D.
12.e3,3e,3π,π3的大小关系是(注:e=2.71828…为自然对数的底数)( )
A.3π>π3>3e>e3 B.3π>π3>e3>3e
C.π3>3π>3e>e3 D.π3>3π>e3>3e
二、填空题(共4小题,每小题3分,满分12分)
13.在(x﹣)5的二次展开式中,x2的系数为 (用数字作答).
14.某省派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,则不同的分配方案共有 种.(用数字填写答案)
15.设命题p:x2﹣4x+3<0,q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.若p是q的充分不必要条件,则实数m的取值范围是 .
16.若函数f(x)=的值域为[2,+∞),给出下列命题:
①f(3)>f(2);
②m≥2;
③f()<f();
④logm(m+1)>logm+1(m+2).
其中所有正确命题的编号是 .
三、解答题(共6小题,满分72分)
17.从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.99.
(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共100件,从中无放回一次性任意抽取2件,用X表示取出的2件产品中二等品的件数,求X的分布列.
18.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.从进入大数据时代以来,人们阅读方式发生了改变,数字媒体阅读方式因为便携,容量大等优点越来越被大众接受,如表是国际数据公司(IDC)研究的全球近6年每年数字媒体阅读产生的数据量(单位:ZB)及相关统计量的值:
年份 2015 2016 2017 2018 2019 2020
序号x 1 2 3 4 5 6
年数据量y 7 9 17 22 34 43
(xi﹣)2 (zi﹣)2 (xi﹣)(yi﹣) (xi﹣)(zi﹣)
3.5 22 2 18 14 124 9
表中zi=lnyi,=zi.
(1)根据表数据信息判断,方程y=c1 e(e是自然对数的底数)更适宜作为该公司统计的年数据量y关于年份序号x的回归方程类型,试求此回归方程;
(2)根据(1)中的回归方程,预计2024年全世界数字媒体阅读产生的数据量是2021年的多少倍?并说明理由.(参考数据:e≈2.718,≈1.648,结果精确到0.1)
参考数据:回归方程=+x中,斜率最小二乘法公式为==,=﹣.
19.如图,在三棱柱ABC﹣A1B1C1中,平面ABC⊥平面ABB1A1,AC⊥AB,H为棱BB1上的点,满足A1H⊥BB1.
(1)求证:A1H⊥平面A1C1CA;
(2)若AC=AB=AA1=2,,求二面角A﹣BB1﹣C1的正切值.
20.已知函数f(x)=a(x﹣1)ex,其中a∈R,且a≠0.
(1)求函数f(x)的单调区间;
(2)当a=1时,设,x0是g(x)的极大值点,求证:.
21.已知椭圆的离心率为,椭圆C1的长轴是圆的直径.
(1)求椭圆C1的标准方程;
(2)过椭圆C1的右焦点F作两条相互垂直的直线l1,l2,其中l1交椭圆C1于P,Q两点,l2交圆C2于M,N两点,求四边形PMQN面积的取值范围.
22.在平面直角坐标系xOy中,已知点P的坐标为(0,2),直线C1的方程为:(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0.
(1)将直线C1的方程化为普通方程,曲线C2的方程化为直角坐标方程;
(2)若直线C1过点Q(,﹣1)且交曲线C2于A,B两点,设线段AB的中点为M,求|PM|.
参考答案
一、选择题(共12小题,每小题3分,满分36分)
1.已知集合A={x|(x+1)(x﹣3)<0},B={1,2,3},则A∩B=( )
A.{x|﹣1<x<3} B.{x|1≤x≤2} C.{1,2,3} D.{1,2}
【分析】可解出集合A,然后进行交集的运算即可.
解:A={x|﹣1<x<3};
∴A∩B={1,2}.
故选:D.
2.设i是虚数单位,若复数z满足(1+i)z=2i,则z=( )
A.﹣1+i B.1﹣i C.1+i D.﹣1﹣i
【分析】(1+i)z=2i,可得(1﹣i)(1+i)z=2i(1﹣i),化简整理即可得出.
解:∵(1+i)z=2i,
∴(1﹣i)(1+i)z=2i(1﹣i),
化为:2z=2(i+1),
∴z=1+i.
故选:C.
3.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为( )
A. B. C. D.
【分析】由题意利用事件发生的频率和概率的定义,得出结论.
解:某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,
那么出现正面朝上的频率为 =0.4.
由于每次抛硬币时,正面朝上和反面朝上的机会相等,都是,
故出现正面朝上的概率为=0.5,
故选:C.
4.如表是某电器销售公司2021年第一季度各类电器营业收入占比和净利润占比统计表:
空调类 冰箱类 小家电类 其他类
营业收入占比 90.10% 4.98% 3.82% 1.10%
净利润占比 95.80% ﹣0.48% 3.82% 0.86%
下列判断中不正确的是( )
A.该公司2021年第一季度冰箱类电器销售亏损
B.该公司2021年第一季度小家电类电器营业收入和净利润相同
C.该公司2021年第一季度净利润主要由空调类电器销售提供
D.剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低
【分析】根据表中数据进行分析,即可依次求解.
解:根据表中数据可得,该公司2021年度冰箱类电器销售净利润占比为﹣0.48%,故A正确,
该公司2021年第一季度小家电类电器营业收入和净利润占比相同,
但收入和净利润不一定相同,故B错误,
该公司2021年第一季度空调类电器销售净利润占比95.8%,
故该公司2021年第一季度净利润主要由空调类电器销售提供,故C正确,
因为冰箱类电器销售净利润占比为﹣0.48%,
故剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低,故D正确.
故选:B.
5.已知p=30.5,q=log95,r=log32,则p,q,r的大小关系为( )
A.q>p>r B.p>r>q C.p>q>r D.r>q>p
【分析】利用指数与对数函数的单调性即可得出.
解:∵p=30.5>1,1>q=log95=>r=log32,
则p,q,r的大小关系为:p>q>r.
故选:C.
6.在区间[﹣2,2]上随机取一个数b,若使直线y=x+b与圆x2+y2=a有交点的概率为,则a=( )
A. B. C.1 D.2
【分析】求出直线与圆有交点时b的范围,再由长度比为求解a值.
解:圆x2+y2=a的圆心为(0,0),半径为,
圆心到直线y=x+b的距离d=,由,可得b∈[﹣,].
∵使直线y=x+b与圆x2+y2=a有交点的概率为,
∴,可得a=.
故选:B.
7.2019年7月,中国良渚古城遗址获准列入世界遗产名录.良渚古城遗址是人类早期城市文明的范例,实证了华夏五千年文明史.考古学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(年)的衰变规律满足:(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log23≈1.6,log25≈2.3)
A.3440年 B.4010年 C.4580年 D.5160年
【分析】由题意可得,求解指数方程可得t值,则答案可求.
解:由题意,可得,即,
两边取以2为底数的对数,可得≈1.6﹣2.3=﹣0.7,
∴t=0.7×5730=4011年.
故选:B.
8.设(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,则下列结论正确的是( )
A.a0=﹣16 B.a0+a1+a2+a3+a4=81
C.a1+a2+a3+a4=15 D.a0+a2+a4=41
【分析】由于(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,因此分别对x赋值0,1和﹣1,对四个选项逐一分析判断即可.
解:∵(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,
令x=0,得a0=16①,故A错误;
令x=1,得a0+a1+a2+a3+a4=(1﹣2)4=1②,故B错误;
由①②得a1+a2+a3+a4=﹣15,故C错误;
令x=﹣1,得a0﹣a1+a2﹣a3+a4=(﹣1﹣2)4=81③,
由②③得a0+a2+a4==41,故D正确;
故选:D.
9.我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的x,y分别为( )
A.90,86 B.94,82 C.98,78 D.102,74
【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量x,y的值,模拟程序的运行过程,可得答案.
解:第一次执行循环体后,y=90,S=,不满足退出循环的条件,故x=90;
第二次执行循环体后,y=86,S=,不满足退出循环的条件,故x=94;
第三次执行循环体后,y=82,S=,不满足退出循环的条件,故x=98;
第四次执行循环体后,y=78,S=27,满足退出循环的条件,
故x=98,y=78
故选:C.
10.已知m>0,xy>0,当x+y=2时,不等式≥4恒成立,则m的取值范围是( )
A.[,+∞) B.[2,+∞) C.(0,] D.(,2]
【分析】根据条件有==,化简后利用基本不等式可得的最小值,然后根据≥4恒成立可得≥4,解出m的范围即可.
解:∵m>0,xy>0,x+y=2,
∴==
≥
=,
∵不等式≥4恒成立,∴≥4,
整理得,解得,即m≥2,
∴m的取值范围为[2,+∞).
故选:B.
11.已知f(x+1)是周期为2的奇函数,当﹣1≤x≤0时,f(x)=sinπx,则的值为( )
A. B. C. D.
【分析】先利用已知条件确定函数f(x)的周期,再利用f(x+1)=﹣f(﹣x+1)和已知的解析式,求解即可.
解:因为f(x+1)是周期为2的函数,
所以f(x)的周期为2,
因为f(x+1)为奇函数,
则f(x+1)=﹣f(﹣x+1),且当﹣1≤x≤0时,f(x)=sinπx,
所以=.
故选:D.
12.e3,3e,3π,π3的大小关系是(注:e=2.71828…为自然对数的底数)( )
A.3π>π3>3e>e3 B.3π>π3>e3>3e
C.π3>3π>3e>e3 D.π3>3π>e3>3e
【分析】利用指数函数的单调性、构造法、导数的性质直接求解.
解:∵e≈2.71828<π≈3.14159,
∴e3<π3,3e<3π,
构造函数f(x)=x﹣elnx,
f(e)=e﹣elne=0,
f′(x)=1﹣,
当x>e时,f′(x)>0,f(x)=x﹣elnx是增函数,
f(3)=3﹣eln3>0,3>eln3=ln3e,
∴e3>3e,
构造函数g(x)=,则g′(x)=,
当x≥e时,g′(x)≤0,∴g(x)在[e,+∞)上单调递减,
又π>3>e,∴,∴3lnπ<πln3,∴3π>π3,
∴3π>π3>e3>3e.
故选:B.
二、填空题(共4小题,每小题3分,满分12分)
13.在(x﹣)5的二次展开式中,x2的系数为 40 (用数字作答).
【分析】利用二项展开式的通项公式求出第r+1项,令x的指数为2求出x2的系数.
解:,
令
所以r=2,
所以x2的系数为(﹣2)2C52=40.
故答案为40
14.某省派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,则不同的分配方案共有 240 种.(用数字填写答案)
【分析】分两步进行分析:先选出一个灾区两个医疗队,再为剩下的3个灾区各分配一个医疗队即可.
解:派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,
则其中有一个灾区安排两个医疗队,剩下的3个灾区各安排一个医疗队,
分两步:
第一步:先选出一个灾区分配两个医疗队,有种分配法;
第二步:为剩下的3个灾区各分配一个医疗队,有种分配法;
所以,不同的分配方案有=240.
故答案为240.
15.设命题p:x2﹣4x+3<0,q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.若p是q的充分不必要条件,则实数m的取值范围是 1≤m≤2 .
【分析】直接利用集合间的关系,进一步利用充分条件和必要条件的应用求出结果.
解:命题p:x2﹣4x+3<0,故A={x|1<x<3},
命题q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.故B={x|m﹣1≤x≤m+2},
由于p是q的充分不必要条件,
故,整理得:1≤m≤2.
故答案为:1≤m≤2.
16.若函数f(x)=的值域为[2,+∞),给出下列命题:
①f(3)>f(2);
②m≥2;
③f()<f();
④logm(m+1)>logm+1(m+2).
其中所有正确命题的编号是 ①②③④ .
【分析】直接利用函数的导数和函数的单调性的关系,构造函数的应用,对数的运算的应用判断①②③④的结论.
解:对于A:对于①,当x≥1时,f(x)=x+1﹣lnx,
则f′(x)=≥0恒成立,所以当x≥1时幂函数为单调递增函数,
故f(3)>f(2),故①正确;
对于②,对于f(x)>f(1)=﹣1+2﹣1+m=m,
由于f(x)≥f(1)=1+1﹣ln1=2,所以f(x)∈[2,+∞),
由于函数的值域为[2,+∞),则(m,+∞) [2,+∞),所以m≥2,故②正确;
对于③,令g(x)=,(x>0),所以g,
令g′(x)>0,解得:0<x<e,令g′(x)<0,整理得:x>e,
所以函数g(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
所以g(2)<g(e),即,
由于当x<1时,f(x)=﹣x3﹣x+2+m显然单调递减,所以f()<f(),故③正确;
对于④,由于,故④正确.
故答案为:①②③④.
三、解答题(共6小题,满分72分)
17.从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.99.
(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共100件,从中无放回一次性任意抽取2件,用X表示取出的2件产品中二等品的件数,求X的分布列.
【分析】(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”,则P(A)=P(A0∪A1)=P(A0)+P(A1)=(1﹣p)2+p(1﹣p)=1﹣p2,由此能求出从该批产品中任取1件是二等品的概率.(2)X的可能取值为0,1,2,由超几何分布能求出X的分布列.
解:(1)设从该批产品中任取1件是二等品的概率为p,
记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”,
则A0,A1互斥,且A=A0∪A1,
故P(A)=P(A0∪A1)=P(A0)+P(A1)=(1﹣p)2+p(1﹣p)=1﹣p2,
即0.96=1﹣p2.解得p=0.1,或p=﹣0.1(舍去).
故从该批产品中任取1件是二等品的概率为0.1.
(2)X的可能取值为0,1,2,
该批产品共100件,由(1)知其二等品有100×0.1=10(件),
故P(X=0)==,
P(X=1)==,
P(X=2)==,
所以X的分布列为:
X 0 1 2
P
18.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.从进入大数据时代以来,人们阅读方式发生了改变,数字媒体阅读方式因为便携,容量大等优点越来越被大众接受,如表是国际数据公司(IDC)研究的全球近6年每年数字媒体阅读产生的数据量(单位:ZB)及相关统计量的值:
年份 2015 2016 2017 2018 2019 2020
序号x 1 2 3 4 5 6
年数据量y 7 9 17 22 34 43
(xi﹣)2 (zi﹣)2 (xi﹣)(yi﹣) (xi﹣)(zi﹣)
3.5 22 2 18 14 124 9
表中zi=lnyi,=zi.
(1)根据表数据信息判断,方程y=c1 e(e是自然对数的底数)更适宜作为该公司统计的年数据量y关于年份序号x的回归方程类型,试求此回归方程;
(2)根据(1)中的回归方程,预计2024年全世界数字媒体阅读产生的数据量是2021年的多少倍?并说明理由.(参考数据:e≈2.718,≈1.648,结果精确到0.1)
参考数据:回归方程=+x中,斜率最小二乘法公式为==,=﹣.
【分析】(1)将方程两边同时取自然对数,转化为z=lnc1+c2x,然后求出样本平均数,求出回归系数,然后求出线性回归方程,从而得到y关于x的回归方程;
(2)分别求出x=7和x=10时的预测值,然后作商即可得到答案.
解:(1)因为方程y=c1 e,两边同时取自然对数可得,lny=ln),
设z=lny,则z=lnc1+c2x,
因为,,,,
所以,
则,
所以z=0.25+0.5x=lny,
故y=e0.25+0.5x;
(2)令x=7,可得,
令x=10,可得,
所以,
故预计2024年全世界数字媒体阅读产生的数据量是2021年的4.5倍.
19.如图,在三棱柱ABC﹣A1B1C1中,平面ABC⊥平面ABB1A1,AC⊥AB,H为棱BB1上的点,满足A1H⊥BB1.
(1)求证:A1H⊥平面A1C1CA;
(2)若AC=AB=AA1=2,,求二面角A﹣BB1﹣C1的正切值.
【分析】(1)先证明AC⊥平面ABB1A1,进一步AC⊥A1H,再证明A1H⊥AA1,进而可证结论.
(2)先作出二面角的平面角,再求解.
【解答】(1)证明:∵平面ABC⊥平面ABB1A1,AC⊥AB,平面ABC∩平面ABB1A1=AB,AC 平面ABC,
∴AC⊥平面ABB1A1,又∵A1H 平面ABB1A1,
∴AC⊥A1H,
∵A1H⊥BB1.A1A∥BB1,∴A1H⊥AA1,
∴又AA1∩AC=A,
∴A1H⊥平面A1C1CA;
(2)连接C1H,由(1)知AC⊥平面ABB1A1,A1H⊥BB1,
所以∠C1HA1为二面角A﹣BB1﹣C1的平面角,
∵AC=AB=AA1=2,,所以,A1C1=2
在Rt△A1HC1中,可得tan∠C1HA1==,
∴二面角A﹣BB1﹣C1的正切值.
20.已知函数f(x)=a(x﹣1)ex,其中a∈R,且a≠0.
(1)求函数f(x)的单调区间;
(2)当a=1时,设,x0是g(x)的极大值点,求证:.
【分析】(1)求出函数的导数,可知导数零点为0,结合a的符号讨论x=0左右的导数符号,确定原函数的单调区间;
(2)先求出g(x)的导数,找出极大值点所在的区间以及极大值点满足的等量关系,代入g(x),研究g(x0)的单调性,求出值域即可.
解:(1)显然f(x)的定义域为R,f′(x)=axex,令f′(x)=0得x=0,
当a>0时,f′(x)>0 x>0,f′(x)<0 x<0,f(x)的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0);
当a<0时,f′(x)>0 x<0,f′(x)<0 x>0,f(x)的单调递减区间为(0,+∞),单调递增区间为(﹣∞,0),
综上可知,a>0时,f(x)的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0);
a<0时,f(x)的单调递减区间为(0,+∞),单调递增区间为(﹣∞,0).
(2)证明:当a=1时,,x∈R,
g′(x)=﹣x2+2x﹣xex=﹣x(ex+x﹣2),令h(x)=ex+x﹣2,显然该函数为单调递增函数,且h(0)=﹣2<0,h(1)=e﹣1>0,
故 x0∈(0,1),使得,即g′(x0)=0,且当x<x0时,h(x)<0,x>x0时,h(x)>0,
所以由g′(x)<0得x<0,或x>x0,g′(x)>0得0<x<x0,
故x0是g(x)的极大值点,且满足,x0∈(0,1),
此时=
=,x0∈(0,1),
,该二次函数图像开口向下,对称轴为x0=2,故g′(x0)在(0,1)上单调递增,
又g′(1)=0,故g′(x0)<0在(0,1)上恒成立,故g(x0)在(0,1)上单调递减,且g(0)=2,g(1)=,
所以.
21.已知椭圆的离心率为,椭圆C1的长轴是圆的直径.
(1)求椭圆C1的标准方程;
(2)过椭圆C1的右焦点F作两条相互垂直的直线l1,l2,其中l1交椭圆C1于P,Q两点,l2交圆C2于M,N两点,求四边形PMQN面积的取值范围.
【分析】(1)由2a=2,e==,解得a,c,又b2=,解得b,即可得出答案.
(2)由(1)可得F(﹣1,0),分三种情况:①当过点F的直线l1的斜率不存在时,②当过点F的直线l1的斜率为0时,③当过点F的直线l1的斜率存在且不为0时,设直线方程,联立椭圆方程,结合韦达定理可得y1+y2,y1y2,由弦长公式可得|PQ|,再计算S四边形PMQN=|MN||PQ|,即可得出答案.
解:(1)由2a=2,得a=,
由e==,得c=1,所以b=1,
所以椭圆的方程为+y2=1.
(2)由(1)可得F(﹣1,0),
①当过点F的直线l1的斜率不存在时,|MN|=2,|PQ|=,
所以S四边形PMQN=|MN||PQ|=×2×=2,
②当过点F的直线l1的斜率为0时,
|MN|=2,|PQ|=2,
这是S四边形PMQN=|MN||PQ|=×2×=2,
③当过点F的直线l1的斜率存在且不为0时,
设直线l1的方程为x=my﹣1,P(x1,y1),Q(x2,y2),
由,得(2+m2)y2﹣2my﹣1=0,
所以y1+y2=,y1y2=,
|PQ|==,
所以S四边形PMQN=|MN||PQ|=×2×=2,
直线l2的方程为mx+y+m=0,
坐标原点O到直线l2的距离d=,
则|MN|=2=2,
所以S四边形PMQN=|MN||PQ|=2×=2,
由2+m2>2,得2>2,
即S四边形PMQN∈(2,2),
综上所述,四边形PMQN的面积的取值范围为[2,2].
22.在平面直角坐标系xOy中,已知点P的坐标为(0,2),直线C1的方程为:(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0.
(1)将直线C1的方程化为普通方程,曲线C2的方程化为直角坐标方程;
(2)若直线C1过点Q(,﹣1)且交曲线C2于A,B两点,设线段AB的中点为M,求|PM|.
【分析】(1)直接利用转换关系,在参数方程,极坐标方程和直角坐标方程之间进行转换;
(2)利用一元二次方程根和系数的关系式的应用和参数的几何意义求出结果
解:(1)直线C1的方程为:(其中t为参数)消去参数转换为普通方程为xsinα﹣ycosα+2cosα=0;
曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0,根据转换为直角坐标方程为.
(2)直线C1过点Q(,﹣1),所以把点的坐标代入xsinα﹣ycosα+2cosα=0;得到,
所以,
所以直线的参数方程为(t为参数),
代入,
得到,
则,
根据参数的几何意义:|PM|=.
一、选择题(共12小题,每小题3分,满分36分).
1.已知集合A={x|(x+1)(x﹣3)<0},B={1,2,3},则A∩B=( )
A.{x|﹣1<x<3} B.{x|1≤x≤2} C.{1,2,3} D.{1,2}
2.设i是虚数单位,若复数z满足(1+i)z=2i,则z=( )
A.﹣1+i B.1﹣i C.1+i D.﹣1﹣i
3.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为( )
A. B. C. D.
4.如表是某电器销售公司2021年第一季度各类电器营业收入占比和净利润占比统计表:
空调类 冰箱类 小家电类 其他类
营业收入占比 90.10% 4.98% 3.82% 1.10%
净利润占比 95.80% ﹣0.48% 3.82% 0.86%
下列判断中不正确的是( )
A.该公司2021年第一季度冰箱类电器销售亏损
B.该公司2021年第一季度小家电类电器营业收入和净利润相同
C.该公司2021年第一季度净利润主要由空调类电器销售提供
D.剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低
5.已知p=30.5,q=log95,r=log32,则p,q,r的大小关系为( )
A.q>p>r B.p>r>q C.p>q>r D.r>q>p
6.在区间[﹣2,2]上随机取一个数b,若使直线y=x+b与圆x2+y2=a有交点的概率为,则a=( )
A. B. C.1 D.2
7.2019年7月,中国良渚古城遗址获准列入世界遗产名录.良渚古城遗址是人类早期城市文明的范例,实证了华夏五千年文明史.考古学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(年)的衰变规律满足:(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log23≈1.6,log25≈2.3)
A.3440年 B.4010年 C.4580年 D.5160年
8.设(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,则下列结论正确的是( )
A.a0=﹣16 B.a0+a1+a2+a3+a4=81
C.a1+a2+a3+a4=15 D.a0+a2+a4=41
9.我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的x,y分别为( )
A.90,86 B.94,82 C.98,78 D.102,74
10.已知m>0,xy>0,当x+y=2时,不等式≥4恒成立,则m的取值范围是( )
A.[,+∞) B.[2,+∞) C.(0,] D.(,2]
11.已知f(x+1)是周期为2的奇函数,当﹣1≤x≤0时,f(x)=sinπx,则的值为( )
A. B. C. D.
12.e3,3e,3π,π3的大小关系是(注:e=2.71828…为自然对数的底数)( )
A.3π>π3>3e>e3 B.3π>π3>e3>3e
C.π3>3π>3e>e3 D.π3>3π>e3>3e
二、填空题(共4小题,每小题3分,满分12分)
13.在(x﹣)5的二次展开式中,x2的系数为 (用数字作答).
14.某省派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,则不同的分配方案共有 种.(用数字填写答案)
15.设命题p:x2﹣4x+3<0,q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.若p是q的充分不必要条件,则实数m的取值范围是 .
16.若函数f(x)=的值域为[2,+∞),给出下列命题:
①f(3)>f(2);
②m≥2;
③f()<f();
④logm(m+1)>logm+1(m+2).
其中所有正确命题的编号是 .
三、解答题(共6小题,满分72分)
17.从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.99.
(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共100件,从中无放回一次性任意抽取2件,用X表示取出的2件产品中二等品的件数,求X的分布列.
18.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.从进入大数据时代以来,人们阅读方式发生了改变,数字媒体阅读方式因为便携,容量大等优点越来越被大众接受,如表是国际数据公司(IDC)研究的全球近6年每年数字媒体阅读产生的数据量(单位:ZB)及相关统计量的值:
年份 2015 2016 2017 2018 2019 2020
序号x 1 2 3 4 5 6
年数据量y 7 9 17 22 34 43
(xi﹣)2 (zi﹣)2 (xi﹣)(yi﹣) (xi﹣)(zi﹣)
3.5 22 2 18 14 124 9
表中zi=lnyi,=zi.
(1)根据表数据信息判断,方程y=c1 e(e是自然对数的底数)更适宜作为该公司统计的年数据量y关于年份序号x的回归方程类型,试求此回归方程;
(2)根据(1)中的回归方程,预计2024年全世界数字媒体阅读产生的数据量是2021年的多少倍?并说明理由.(参考数据:e≈2.718,≈1.648,结果精确到0.1)
参考数据:回归方程=+x中,斜率最小二乘法公式为==,=﹣.
19.如图,在三棱柱ABC﹣A1B1C1中,平面ABC⊥平面ABB1A1,AC⊥AB,H为棱BB1上的点,满足A1H⊥BB1.
(1)求证:A1H⊥平面A1C1CA;
(2)若AC=AB=AA1=2,,求二面角A﹣BB1﹣C1的正切值.
20.已知函数f(x)=a(x﹣1)ex,其中a∈R,且a≠0.
(1)求函数f(x)的单调区间;
(2)当a=1时,设,x0是g(x)的极大值点,求证:.
21.已知椭圆的离心率为,椭圆C1的长轴是圆的直径.
(1)求椭圆C1的标准方程;
(2)过椭圆C1的右焦点F作两条相互垂直的直线l1,l2,其中l1交椭圆C1于P,Q两点,l2交圆C2于M,N两点,求四边形PMQN面积的取值范围.
22.在平面直角坐标系xOy中,已知点P的坐标为(0,2),直线C1的方程为:(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0.
(1)将直线C1的方程化为普通方程,曲线C2的方程化为直角坐标方程;
(2)若直线C1过点Q(,﹣1)且交曲线C2于A,B两点,设线段AB的中点为M,求|PM|.
参考答案
一、选择题(共12小题,每小题3分,满分36分)
1.已知集合A={x|(x+1)(x﹣3)<0},B={1,2,3},则A∩B=( )
A.{x|﹣1<x<3} B.{x|1≤x≤2} C.{1,2,3} D.{1,2}
【分析】可解出集合A,然后进行交集的运算即可.
解:A={x|﹣1<x<3};
∴A∩B={1,2}.
故选:D.
2.设i是虚数单位,若复数z满足(1+i)z=2i,则z=( )
A.﹣1+i B.1﹣i C.1+i D.﹣1﹣i
【分析】(1+i)z=2i,可得(1﹣i)(1+i)z=2i(1﹣i),化简整理即可得出.
解:∵(1+i)z=2i,
∴(1﹣i)(1+i)z=2i(1﹣i),
化为:2z=2(i+1),
∴z=1+i.
故选:C.
3.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为( )
A. B. C. D.
【分析】由题意利用事件发生的频率和概率的定义,得出结论.
解:某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,
那么出现正面朝上的频率为 =0.4.
由于每次抛硬币时,正面朝上和反面朝上的机会相等,都是,
故出现正面朝上的概率为=0.5,
故选:C.
4.如表是某电器销售公司2021年第一季度各类电器营业收入占比和净利润占比统计表:
空调类 冰箱类 小家电类 其他类
营业收入占比 90.10% 4.98% 3.82% 1.10%
净利润占比 95.80% ﹣0.48% 3.82% 0.86%
下列判断中不正确的是( )
A.该公司2021年第一季度冰箱类电器销售亏损
B.该公司2021年第一季度小家电类电器营业收入和净利润相同
C.该公司2021年第一季度净利润主要由空调类电器销售提供
D.剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低
【分析】根据表中数据进行分析,即可依次求解.
解:根据表中数据可得,该公司2021年度冰箱类电器销售净利润占比为﹣0.48%,故A正确,
该公司2021年第一季度小家电类电器营业收入和净利润占比相同,
但收入和净利润不一定相同,故B错误,
该公司2021年第一季度空调类电器销售净利润占比95.8%,
故该公司2021年第一季度净利润主要由空调类电器销售提供,故C正确,
因为冰箱类电器销售净利润占比为﹣0.48%,
故剔除冰箱类的销售数据,该公司2021年第一季度空调类电器销售净利润占比将会降低,故D正确.
故选:B.
5.已知p=30.5,q=log95,r=log32,则p,q,r的大小关系为( )
A.q>p>r B.p>r>q C.p>q>r D.r>q>p
【分析】利用指数与对数函数的单调性即可得出.
解:∵p=30.5>1,1>q=log95=>r=log32,
则p,q,r的大小关系为:p>q>r.
故选:C.
6.在区间[﹣2,2]上随机取一个数b,若使直线y=x+b与圆x2+y2=a有交点的概率为,则a=( )
A. B. C.1 D.2
【分析】求出直线与圆有交点时b的范围,再由长度比为求解a值.
解:圆x2+y2=a的圆心为(0,0),半径为,
圆心到直线y=x+b的距离d=,由,可得b∈[﹣,].
∵使直线y=x+b与圆x2+y2=a有交点的概率为,
∴,可得a=.
故选:B.
7.2019年7月,中国良渚古城遗址获准列入世界遗产名录.良渚古城遗址是人类早期城市文明的范例,实证了华夏五千年文明史.考古学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(年)的衰变规律满足:(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log23≈1.6,log25≈2.3)
A.3440年 B.4010年 C.4580年 D.5160年
【分析】由题意可得,求解指数方程可得t值,则答案可求.
解:由题意,可得,即,
两边取以2为底数的对数,可得≈1.6﹣2.3=﹣0.7,
∴t=0.7×5730=4011年.
故选:B.
8.设(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,则下列结论正确的是( )
A.a0=﹣16 B.a0+a1+a2+a3+a4=81
C.a1+a2+a3+a4=15 D.a0+a2+a4=41
【分析】由于(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,因此分别对x赋值0,1和﹣1,对四个选项逐一分析判断即可.
解:∵(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4,
令x=0,得a0=16①,故A错误;
令x=1,得a0+a1+a2+a3+a4=(1﹣2)4=1②,故B错误;
由①②得a1+a2+a3+a4=﹣15,故C错误;
令x=﹣1,得a0﹣a1+a2﹣a3+a4=(﹣1﹣2)4=81③,
由②③得a0+a2+a4==41,故D正确;
故选:D.
9.我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的x,y分别为( )
A.90,86 B.94,82 C.98,78 D.102,74
【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量x,y的值,模拟程序的运行过程,可得答案.
解:第一次执行循环体后,y=90,S=,不满足退出循环的条件,故x=90;
第二次执行循环体后,y=86,S=,不满足退出循环的条件,故x=94;
第三次执行循环体后,y=82,S=,不满足退出循环的条件,故x=98;
第四次执行循环体后,y=78,S=27,满足退出循环的条件,
故x=98,y=78
故选:C.
10.已知m>0,xy>0,当x+y=2时,不等式≥4恒成立,则m的取值范围是( )
A.[,+∞) B.[2,+∞) C.(0,] D.(,2]
【分析】根据条件有==,化简后利用基本不等式可得的最小值,然后根据≥4恒成立可得≥4,解出m的范围即可.
解:∵m>0,xy>0,x+y=2,
∴==
≥
=,
∵不等式≥4恒成立,∴≥4,
整理得,解得,即m≥2,
∴m的取值范围为[2,+∞).
故选:B.
11.已知f(x+1)是周期为2的奇函数,当﹣1≤x≤0时,f(x)=sinπx,则的值为( )
A. B. C. D.
【分析】先利用已知条件确定函数f(x)的周期,再利用f(x+1)=﹣f(﹣x+1)和已知的解析式,求解即可.
解:因为f(x+1)是周期为2的函数,
所以f(x)的周期为2,
因为f(x+1)为奇函数,
则f(x+1)=﹣f(﹣x+1),且当﹣1≤x≤0时,f(x)=sinπx,
所以=.
故选:D.
12.e3,3e,3π,π3的大小关系是(注:e=2.71828…为自然对数的底数)( )
A.3π>π3>3e>e3 B.3π>π3>e3>3e
C.π3>3π>3e>e3 D.π3>3π>e3>3e
【分析】利用指数函数的单调性、构造法、导数的性质直接求解.
解:∵e≈2.71828<π≈3.14159,
∴e3<π3,3e<3π,
构造函数f(x)=x﹣elnx,
f(e)=e﹣elne=0,
f′(x)=1﹣,
当x>e时,f′(x)>0,f(x)=x﹣elnx是增函数,
f(3)=3﹣eln3>0,3>eln3=ln3e,
∴e3>3e,
构造函数g(x)=,则g′(x)=,
当x≥e时,g′(x)≤0,∴g(x)在[e,+∞)上单调递减,
又π>3>e,∴,∴3lnπ<πln3,∴3π>π3,
∴3π>π3>e3>3e.
故选:B.
二、填空题(共4小题,每小题3分,满分12分)
13.在(x﹣)5的二次展开式中,x2的系数为 40 (用数字作答).
【分析】利用二项展开式的通项公式求出第r+1项,令x的指数为2求出x2的系数.
解:,
令
所以r=2,
所以x2的系数为(﹣2)2C52=40.
故答案为40
14.某省派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,则不同的分配方案共有 240 种.(用数字填写答案)
【分析】分两步进行分析:先选出一个灾区两个医疗队,再为剩下的3个灾区各分配一个医疗队即可.
解:派出5个医疗队去支援4个灾区,每个灾区至少分配一个医疗队,
则其中有一个灾区安排两个医疗队,剩下的3个灾区各安排一个医疗队,
分两步:
第一步:先选出一个灾区分配两个医疗队,有种分配法;
第二步:为剩下的3个灾区各分配一个医疗队,有种分配法;
所以,不同的分配方案有=240.
故答案为240.
15.设命题p:x2﹣4x+3<0,q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.若p是q的充分不必要条件,则实数m的取值范围是 1≤m≤2 .
【分析】直接利用集合间的关系,进一步利用充分条件和必要条件的应用求出结果.
解:命题p:x2﹣4x+3<0,故A={x|1<x<3},
命题q:x2﹣(2m+1)x+(m﹣1)(m+2)≤0.故B={x|m﹣1≤x≤m+2},
由于p是q的充分不必要条件,
故,整理得:1≤m≤2.
故答案为:1≤m≤2.
16.若函数f(x)=的值域为[2,+∞),给出下列命题:
①f(3)>f(2);
②m≥2;
③f()<f();
④logm(m+1)>logm+1(m+2).
其中所有正确命题的编号是 ①②③④ .
【分析】直接利用函数的导数和函数的单调性的关系,构造函数的应用,对数的运算的应用判断①②③④的结论.
解:对于A:对于①,当x≥1时,f(x)=x+1﹣lnx,
则f′(x)=≥0恒成立,所以当x≥1时幂函数为单调递增函数,
故f(3)>f(2),故①正确;
对于②,对于f(x)>f(1)=﹣1+2﹣1+m=m,
由于f(x)≥f(1)=1+1﹣ln1=2,所以f(x)∈[2,+∞),
由于函数的值域为[2,+∞),则(m,+∞) [2,+∞),所以m≥2,故②正确;
对于③,令g(x)=,(x>0),所以g,
令g′(x)>0,解得:0<x<e,令g′(x)<0,整理得:x>e,
所以函数g(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
所以g(2)<g(e),即,
由于当x<1时,f(x)=﹣x3﹣x+2+m显然单调递减,所以f()<f(),故③正确;
对于④,由于,故④正确.
故答案为:①②③④.
三、解答题(共6小题,满分72分)
17.从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.99.
(1)求从该批产品中任取1件是二等品的概率p;
(2)若该批产品共100件,从中无放回一次性任意抽取2件,用X表示取出的2件产品中二等品的件数,求X的分布列.
【分析】(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”,则P(A)=P(A0∪A1)=P(A0)+P(A1)=(1﹣p)2+p(1﹣p)=1﹣p2,由此能求出从该批产品中任取1件是二等品的概率.(2)X的可能取值为0,1,2,由超几何分布能求出X的分布列.
解:(1)设从该批产品中任取1件是二等品的概率为p,
记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”,
则A0,A1互斥,且A=A0∪A1,
故P(A)=P(A0∪A1)=P(A0)+P(A1)=(1﹣p)2+p(1﹣p)=1﹣p2,
即0.96=1﹣p2.解得p=0.1,或p=﹣0.1(舍去).
故从该批产品中任取1件是二等品的概率为0.1.
(2)X的可能取值为0,1,2,
该批产品共100件,由(1)知其二等品有100×0.1=10(件),
故P(X=0)==,
P(X=1)==,
P(X=2)==,
所以X的分布列为:
X 0 1 2
P
18.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.从进入大数据时代以来,人们阅读方式发生了改变,数字媒体阅读方式因为便携,容量大等优点越来越被大众接受,如表是国际数据公司(IDC)研究的全球近6年每年数字媒体阅读产生的数据量(单位:ZB)及相关统计量的值:
年份 2015 2016 2017 2018 2019 2020
序号x 1 2 3 4 5 6
年数据量y 7 9 17 22 34 43
(xi﹣)2 (zi﹣)2 (xi﹣)(yi﹣) (xi﹣)(zi﹣)
3.5 22 2 18 14 124 9
表中zi=lnyi,=zi.
(1)根据表数据信息判断,方程y=c1 e(e是自然对数的底数)更适宜作为该公司统计的年数据量y关于年份序号x的回归方程类型,试求此回归方程;
(2)根据(1)中的回归方程,预计2024年全世界数字媒体阅读产生的数据量是2021年的多少倍?并说明理由.(参考数据:e≈2.718,≈1.648,结果精确到0.1)
参考数据:回归方程=+x中,斜率最小二乘法公式为==,=﹣.
【分析】(1)将方程两边同时取自然对数,转化为z=lnc1+c2x,然后求出样本平均数,求出回归系数,然后求出线性回归方程,从而得到y关于x的回归方程;
(2)分别求出x=7和x=10时的预测值,然后作商即可得到答案.
解:(1)因为方程y=c1 e,两边同时取自然对数可得,lny=ln),
设z=lny,则z=lnc1+c2x,
因为,,,,
所以,
则,
所以z=0.25+0.5x=lny,
故y=e0.25+0.5x;
(2)令x=7,可得,
令x=10,可得,
所以,
故预计2024年全世界数字媒体阅读产生的数据量是2021年的4.5倍.
19.如图,在三棱柱ABC﹣A1B1C1中,平面ABC⊥平面ABB1A1,AC⊥AB,H为棱BB1上的点,满足A1H⊥BB1.
(1)求证:A1H⊥平面A1C1CA;
(2)若AC=AB=AA1=2,,求二面角A﹣BB1﹣C1的正切值.
【分析】(1)先证明AC⊥平面ABB1A1,进一步AC⊥A1H,再证明A1H⊥AA1,进而可证结论.
(2)先作出二面角的平面角,再求解.
【解答】(1)证明:∵平面ABC⊥平面ABB1A1,AC⊥AB,平面ABC∩平面ABB1A1=AB,AC 平面ABC,
∴AC⊥平面ABB1A1,又∵A1H 平面ABB1A1,
∴AC⊥A1H,
∵A1H⊥BB1.A1A∥BB1,∴A1H⊥AA1,
∴又AA1∩AC=A,
∴A1H⊥平面A1C1CA;
(2)连接C1H,由(1)知AC⊥平面ABB1A1,A1H⊥BB1,
所以∠C1HA1为二面角A﹣BB1﹣C1的平面角,
∵AC=AB=AA1=2,,所以,A1C1=2
在Rt△A1HC1中,可得tan∠C1HA1==,
∴二面角A﹣BB1﹣C1的正切值.
20.已知函数f(x)=a(x﹣1)ex,其中a∈R,且a≠0.
(1)求函数f(x)的单调区间;
(2)当a=1时,设,x0是g(x)的极大值点,求证:.
【分析】(1)求出函数的导数,可知导数零点为0,结合a的符号讨论x=0左右的导数符号,确定原函数的单调区间;
(2)先求出g(x)的导数,找出极大值点所在的区间以及极大值点满足的等量关系,代入g(x),研究g(x0)的单调性,求出值域即可.
解:(1)显然f(x)的定义域为R,f′(x)=axex,令f′(x)=0得x=0,
当a>0时,f′(x)>0 x>0,f′(x)<0 x<0,f(x)的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0);
当a<0时,f′(x)>0 x<0,f′(x)<0 x>0,f(x)的单调递减区间为(0,+∞),单调递增区间为(﹣∞,0),
综上可知,a>0时,f(x)的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0);
a<0时,f(x)的单调递减区间为(0,+∞),单调递增区间为(﹣∞,0).
(2)证明:当a=1时,,x∈R,
g′(x)=﹣x2+2x﹣xex=﹣x(ex+x﹣2),令h(x)=ex+x﹣2,显然该函数为单调递增函数,且h(0)=﹣2<0,h(1)=e﹣1>0,
故 x0∈(0,1),使得,即g′(x0)=0,且当x<x0时,h(x)<0,x>x0时,h(x)>0,
所以由g′(x)<0得x<0,或x>x0,g′(x)>0得0<x<x0,
故x0是g(x)的极大值点,且满足,x0∈(0,1),
此时=
=,x0∈(0,1),
,该二次函数图像开口向下,对称轴为x0=2,故g′(x0)在(0,1)上单调递增,
又g′(1)=0,故g′(x0)<0在(0,1)上恒成立,故g(x0)在(0,1)上单调递减,且g(0)=2,g(1)=,
所以.
21.已知椭圆的离心率为,椭圆C1的长轴是圆的直径.
(1)求椭圆C1的标准方程;
(2)过椭圆C1的右焦点F作两条相互垂直的直线l1,l2,其中l1交椭圆C1于P,Q两点,l2交圆C2于M,N两点,求四边形PMQN面积的取值范围.
【分析】(1)由2a=2,e==,解得a,c,又b2=,解得b,即可得出答案.
(2)由(1)可得F(﹣1,0),分三种情况:①当过点F的直线l1的斜率不存在时,②当过点F的直线l1的斜率为0时,③当过点F的直线l1的斜率存在且不为0时,设直线方程,联立椭圆方程,结合韦达定理可得y1+y2,y1y2,由弦长公式可得|PQ|,再计算S四边形PMQN=|MN||PQ|,即可得出答案.
解:(1)由2a=2,得a=,
由e==,得c=1,所以b=1,
所以椭圆的方程为+y2=1.
(2)由(1)可得F(﹣1,0),
①当过点F的直线l1的斜率不存在时,|MN|=2,|PQ|=,
所以S四边形PMQN=|MN||PQ|=×2×=2,
②当过点F的直线l1的斜率为0时,
|MN|=2,|PQ|=2,
这是S四边形PMQN=|MN||PQ|=×2×=2,
③当过点F的直线l1的斜率存在且不为0时,
设直线l1的方程为x=my﹣1,P(x1,y1),Q(x2,y2),
由,得(2+m2)y2﹣2my﹣1=0,
所以y1+y2=,y1y2=,
|PQ|==,
所以S四边形PMQN=|MN||PQ|=×2×=2,
直线l2的方程为mx+y+m=0,
坐标原点O到直线l2的距离d=,
则|MN|=2=2,
所以S四边形PMQN=|MN||PQ|=2×=2,
由2+m2>2,得2>2,
即S四边形PMQN∈(2,2),
综上所述,四边形PMQN的面积的取值范围为[2,2].
22.在平面直角坐标系xOy中,已知点P的坐标为(0,2),直线C1的方程为:(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0.
(1)将直线C1的方程化为普通方程,曲线C2的方程化为直角坐标方程;
(2)若直线C1过点Q(,﹣1)且交曲线C2于A,B两点,设线段AB的中点为M,求|PM|.
【分析】(1)直接利用转换关系,在参数方程,极坐标方程和直角坐标方程之间进行转换;
(2)利用一元二次方程根和系数的关系式的应用和参数的几何意义求出结果
解:(1)直线C1的方程为:(其中t为参数)消去参数转换为普通方程为xsinα﹣ycosα+2cosα=0;
曲线C2的极坐标方程为:ρcos2θ+4cosθ﹣ρ=0,根据转换为直角坐标方程为.
(2)直线C1过点Q(,﹣1),所以把点的坐标代入xsinα﹣ycosα+2cosα=0;得到,
所以,
所以直线的参数方程为(t为参数),
代入,
得到,
则,
根据参数的几何意义:|PM|=.
同课章节目录
