2021-2022学年数学人教A版(2019)必修第一册3.1.2函数的表示法强化训练
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册3.1.2函数的表示法强化训练 | 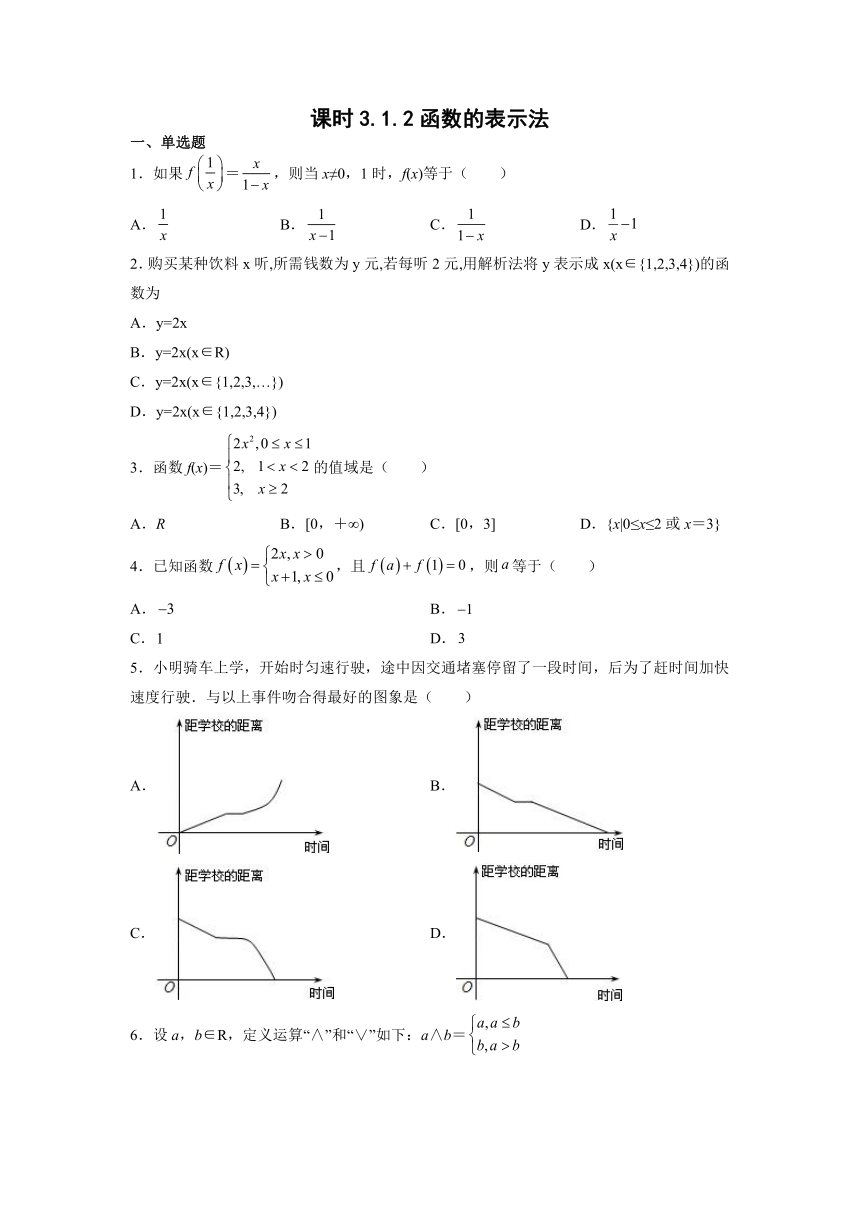 | |
| 格式 | docx | ||
| 文件大小 | 516.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 10:50:45 | ||
图片预览




文档简介
课时3.1.2函数的表示法
一、单选题
1.如果=,则当x≠0,1时,f(x)等于( )
A. B. C. D.
2.购买某种饮料x听,所需钱数为y元,若每听2元,用解析法将y表示成x(x∈{1,2,3,4})的函数为
A.y=2x
B.y=2x(x∈R)
C.y=2x(x∈{1,2,3,…})
D.y=2x(x∈{1,2,3,4})
3.函数f(x)=的值域是( )
A.R B.[0,+∞) C.[0,3] D.{x|0≤x≤2或x=3}
4.已知函数,且,则等于( )
A. B.
C. D.
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
6.设a,b∈R,定义运算“∧”和“∨”如下:a∧b=
a∨b=若正数a,b,c,d满足ab≥4,c+d≤4,则( )
A.a∧b≥2,c∧d≤2 B.a∧b≥2,c∨d≥2
C.a∨b≥2,c∧d≤2 D.a∨b≥2,c∨d≥2
7.已知函数的对应关系如下表,函数的图象是如图的曲线,其中,,,则的值为( )
A.3 B.0 C.1 D.2
8.设函数在上有定义,对于任一给定的正数,定义函数,则称函数为的“界函数”,若给定函数,,则下列结论不成立的是
A. B.
C. D.
二、多选题
9.下列给出的式子是分段函数的是( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
10.设函数,若则实数a=( )
A.2 B.-2 C.4 D.-4
11.(多选)已知函数 则下列关于函数的结论正确的是( )
A.的值域为
B.
C.若,则的值是
D.的解集为
12.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
三、填空题
13.已知且,则a的值为________.
14.已知f(x)=,则的值等于________.
15.已知函数满足,则的解析式为________.
16.分段函数可表示为,分段函数可表示为,仿照上述式子,分段函数可表示为________.
四、解答题
17.设是上的函数,且满足,并且对任意实数,,有,求的解析式
18.若直线y=1与曲线y=x2-|x|+a有四个交点,求a的取值范围.
19.(1)已知,求的解析式.
(2)已知满足,求的解析式.
(3)已知,求的解析式.
20.如图,已知,,点P从B点沿直线BC运动到C点,过P做BC的垂线l,记直线l左侧部分的多边形为Ω,设,Ω的面积为,Ω的周长为.
(1)求和的解析式;
(2)记,求的最大值.
参考答案
1.B
【解析】令=t,则x=且,代入=,
则有f(t)==且,
即且.
故选:.
2.D
【解析】题中已给出自变量的取值范围,x∈{1,2,3,4},故选D.
3.D
【解析】当0≤x≤1时,f(x)∈[0,2],当1∴值域是{x|0≤x≤2或x=3}.
故选:D
4.A
【解析】,.
当时,,此时关于的方程无解;
当时,,由可得,解得.
综上所述,.
故选:A.
5.C
【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图象一定是下降的,由此排除A;
再由小明骑车上学,开始时匀速行驶可得出图象开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图象与x轴平行,由此排除D,
之后为了赶时间加快速度行驶,此一段时间段内函数图象下降的比较快,由此可确定C正确,B不正确.
故选C.
6.C
【解析】不妨设a≤b,c≤d,则a∨b=b,c∧d=c.
若b<2,则a<2,∴ab<4,与ab≥4矛盾,∴b≥2.故a∨b≥2.
若c>2,则d>2,∴c+d>4,与c+d≤4矛盾,∴c≤2.故c∧d≤2.
本题选择C选项.
7.D
【解析】由图象可知,由表格可知,∴,故选D.
8.B
【解析】根据题意写成,的分段函数形式即,A.,,故A成立;B,,故B不成立;C:,,故C成立;D,,故D成立;所以只有B结论不正确,故选B.
9.AD
【解析】解:对于A:,定义域为,且,符合函数定义,且在定义域的不同区间,有不同的对应关系,故A正确;
对于B:,定义域为,但不满足函数的定义,如当时,和,故不是函数,故B错误;
对于C:,定义域为,且,且和,故不是函数,故C错误;
对于D:,定义域为,且,符合函数定义,且在定义域的不同区间,有不同的对应关系,故D正确;
故选:AD
10.AD
【解析】因为函数,且
所以或,解得a=-4或a=2.
故选:AD.
11.AC
【解析】当时,的取值范围是,当时,的取值范围是,因此的值域为,故A正确;
当时,,故B错误;
当时,由,解得(舍去),当时,由,解得或(舍去),故C正确;
当时,由,解得,当时,由,解得,因此的解集为,故D错误.
故选:AC.
12.BD
【解析】由题意知函数的定义域为,故A错误;
当时,的取值范围是,当时,的取值范围是,因此的值域为,故B正确;
当时,,故C错误;
当时,,解得(舍去),当时,,解得
或(舍去),故D正确;
当时,,解得,当时,,解得,因此的解集为;故E错误.
故选:BD.
13.
【解析】设,则,
因为,所以,即,
又因为,可得,解得.
故答案为:.
14.4
【解析】解析:∵>0,∴=2×=;∵-≤0,∴==;
∵-≤0,∴==;
∵>0,∴=2×=,∴+=+=4.
故答案为:4.
15.
【解析】,∴将x换成,得,
消去,得,即.
故答案为
16.
【解析】解析因为可表示为,其分界点为3,
从而式子中含有与,并通过前面的“-”构造出需要的结果的形式,
所以对于分段函数,其分界点为6,故式子中应含有与.
又时,故的前面应取“”.
因此,经检验符合题意.
故答案为:
17.
【解析】对任意实数,,,令,得,即又,∴
18.
【解析】如图,作出y=x2-|x|+a的图象,
若要使y=1与其有四个交点,则需满足,解得
19.(1) (或);(2);(3).
【解析】(1)∵,且或,
∴ (或).
(2)∵①,把①中的x换成,得2f()+f(x)=②, ①×2-②得3f(x)=6x-,
∴.
(3)∵,用-x代x得:f(-x)+2f(x)=x2-2x,
两式联立得:.
20.(1);(2).
【解析】(1)作的高,,,
当,,所以,,,.
当,,所以,,;
(2)当,,最大值为.
当时,,
当且仅当时,有最大值,又,
故最大值为.
一、单选题
1.如果=,则当x≠0,1时,f(x)等于( )
A. B. C. D.
2.购买某种饮料x听,所需钱数为y元,若每听2元,用解析法将y表示成x(x∈{1,2,3,4})的函数为
A.y=2x
B.y=2x(x∈R)
C.y=2x(x∈{1,2,3,…})
D.y=2x(x∈{1,2,3,4})
3.函数f(x)=的值域是( )
A.R B.[0,+∞) C.[0,3] D.{x|0≤x≤2或x=3}
4.已知函数,且,则等于( )
A. B.
C. D.
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
6.设a,b∈R,定义运算“∧”和“∨”如下:a∧b=
a∨b=若正数a,b,c,d满足ab≥4,c+d≤4,则( )
A.a∧b≥2,c∧d≤2 B.a∧b≥2,c∨d≥2
C.a∨b≥2,c∧d≤2 D.a∨b≥2,c∨d≥2
7.已知函数的对应关系如下表,函数的图象是如图的曲线,其中,,,则的值为( )
A.3 B.0 C.1 D.2
8.设函数在上有定义,对于任一给定的正数,定义函数,则称函数为的“界函数”,若给定函数,,则下列结论不成立的是
A. B.
C. D.
二、多选题
9.下列给出的式子是分段函数的是( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
10.设函数,若则实数a=( )
A.2 B.-2 C.4 D.-4
11.(多选)已知函数 则下列关于函数的结论正确的是( )
A.的值域为
B.
C.若,则的值是
D.的解集为
12.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
三、填空题
13.已知且,则a的值为________.
14.已知f(x)=,则的值等于________.
15.已知函数满足,则的解析式为________.
16.分段函数可表示为,分段函数可表示为,仿照上述式子,分段函数可表示为________.
四、解答题
17.设是上的函数,且满足,并且对任意实数,,有,求的解析式
18.若直线y=1与曲线y=x2-|x|+a有四个交点,求a的取值范围.
19.(1)已知,求的解析式.
(2)已知满足,求的解析式.
(3)已知,求的解析式.
20.如图,已知,,点P从B点沿直线BC运动到C点,过P做BC的垂线l,记直线l左侧部分的多边形为Ω,设,Ω的面积为,Ω的周长为.
(1)求和的解析式;
(2)记,求的最大值.
参考答案
1.B
【解析】令=t,则x=且,代入=,
则有f(t)==且,
即且.
故选:.
2.D
【解析】题中已给出自变量的取值范围,x∈{1,2,3,4},故选D.
3.D
【解析】当0≤x≤1时,f(x)∈[0,2],当1
故选:D
4.A
【解析】,.
当时,,此时关于的方程无解;
当时,,由可得,解得.
综上所述,.
故选:A.
5.C
【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图象一定是下降的,由此排除A;
再由小明骑车上学,开始时匀速行驶可得出图象开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图象与x轴平行,由此排除D,
之后为了赶时间加快速度行驶,此一段时间段内函数图象下降的比较快,由此可确定C正确,B不正确.
故选C.
6.C
【解析】不妨设a≤b,c≤d,则a∨b=b,c∧d=c.
若b<2,则a<2,∴ab<4,与ab≥4矛盾,∴b≥2.故a∨b≥2.
若c>2,则d>2,∴c+d>4,与c+d≤4矛盾,∴c≤2.故c∧d≤2.
本题选择C选项.
7.D
【解析】由图象可知,由表格可知,∴,故选D.
8.B
【解析】根据题意写成,的分段函数形式即,A.,,故A成立;B,,故B不成立;C:,,故C成立;D,,故D成立;所以只有B结论不正确,故选B.
9.AD
【解析】解:对于A:,定义域为,且,符合函数定义,且在定义域的不同区间,有不同的对应关系,故A正确;
对于B:,定义域为,但不满足函数的定义,如当时,和,故不是函数,故B错误;
对于C:,定义域为,且,且和,故不是函数,故C错误;
对于D:,定义域为,且,符合函数定义,且在定义域的不同区间,有不同的对应关系,故D正确;
故选:AD
10.AD
【解析】因为函数,且
所以或,解得a=-4或a=2.
故选:AD.
11.AC
【解析】当时,的取值范围是,当时,的取值范围是,因此的值域为,故A正确;
当时,,故B错误;
当时,由,解得(舍去),当时,由,解得或(舍去),故C正确;
当时,由,解得,当时,由,解得,因此的解集为,故D错误.
故选:AC.
12.BD
【解析】由题意知函数的定义域为,故A错误;
当时,的取值范围是,当时,的取值范围是,因此的值域为,故B正确;
当时,,故C错误;
当时,,解得(舍去),当时,,解得
或(舍去),故D正确;
当时,,解得,当时,,解得,因此的解集为;故E错误.
故选:BD.
13.
【解析】设,则,
因为,所以,即,
又因为,可得,解得.
故答案为:.
14.4
【解析】解析:∵>0,∴=2×=;∵-≤0,∴==;
∵-≤0,∴==;
∵>0,∴=2×=,∴+=+=4.
故答案为:4.
15.
【解析】,∴将x换成,得,
消去,得,即.
故答案为
16.
【解析】解析因为可表示为,其分界点为3,
从而式子中含有与,并通过前面的“-”构造出需要的结果的形式,
所以对于分段函数,其分界点为6,故式子中应含有与.
又时,故的前面应取“”.
因此,经检验符合题意.
故答案为:
17.
【解析】对任意实数,,,令,得,即又,∴
18.
【解析】如图,作出y=x2-|x|+a的图象,
若要使y=1与其有四个交点,则需满足,解得
19.(1) (或);(2);(3).
【解析】(1)∵,且或,
∴ (或).
(2)∵①,把①中的x换成,得2f()+f(x)=②, ①×2-②得3f(x)=6x-,
∴.
(3)∵,用-x代x得:f(-x)+2f(x)=x2-2x,
两式联立得:.
20.(1);(2).
【解析】(1)作的高,,,
当,,所以,,,.
当,,所以,,;
(2)当,,最大值为.
当时,,
当且仅当时,有最大值,又,
故最大值为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
