2021-2022学年数学人教A版(2019)必修第一册4.4.3 不同函数增长的差异 强化训练
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册4.4.3 不同函数增长的差异 强化训练 |
|
|
| 格式 | docx | ||
| 文件大小 | 308.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览





文档简介
4.4.3 不同函数增长的差异 强化训练
一、单选题
1.在固定电压差(电压为常数)的前提下,当电流通过圆柱形的电线时,其电流强度I(单位:安)与电线半径r(单位:毫米)的三次方成正比.若已知电流通过半径为4毫米的电线时,电流强度为320安,则电流通过半径为3毫米的电线时,电流强度为( )
A.60安 B.240安 C.75安 D.135安
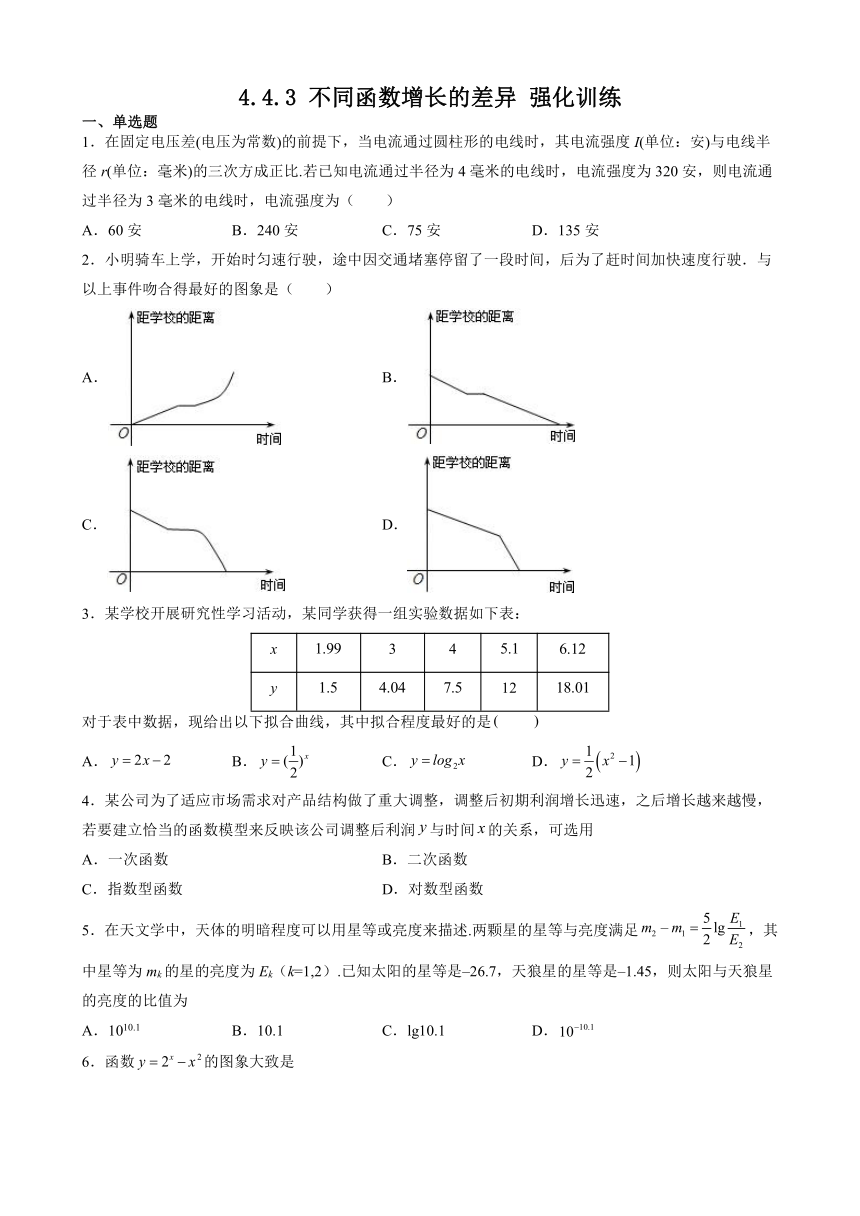
2.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
3.某学校开展研究性学习活动,某同学获得一组实验数据如下表:
x 3 4
y 12
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是
A. B. C. D.
4.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润与时间的关系,可选用
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
5.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
6.函数的图象大致是
A.B.C. D.
7.已知,则
A. B.
C. D.
8.下面对函数与 在区间上的衰减情况说法正确的是( )
A.衰减速度越来越慢,衰减速度越来越快,衰减速度越来越慢
B.衰减速度越来越快,衰减速度越来越慢,衰减速度越来越快
C.衰减速度越来越慢,衰减速度越来越慢,衰减速度越来越慢
D.衰减速度越来越快,衰减速度越来越快,衰减速度越来越快
二、填空题
9.函数与函数在区间上增长较快的一个是________.
10.在某种金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示.
现给出下列说法:
①前5min温度增加的速度越来越快;②前5min温度增加的速度越来越慢;③5min以后温度保持匀速增加;④5min以后温度保持不变.
其中正确的说法是________.(填序号)
11.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图象.有以下叙述:
①第4个月时,剩留量就会低于;
②每月减少的有害物质量都相等;
③若剩留量为,,时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确叙述的序号是________.
12.若函数在区间内单调递增,则实数的取值范围为___.
三、解答题
13.某国2016年至2019年国内生产总值(单位:万亿元)如下表所示:
年份 2016 2017 2018 2019
x(年份代码) 0 1 2 3
生产总值y(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
(1)画出函数图象,猜想y与x之间的函数关系,近似地写出一个函数关系式;
(2)利用得出的关系式求生产总值,与表中实际生产总值比较;
(3)利用关系式预测2033年该国的国内生产总值.
14.某品牌汽车的月产能y(万辆)与月份x(3<x≤12且x∈N)满足关系式.现已知该品牌汽车今年4月、5月的产能分别为1万辆和1.5万辆,求该品牌汽车7月的产能为多少万辆.
15.某鞋厂从今年1月份开始投产,并且前四个月的产量分别为1万件、1.2万件、1.3万件、1.37万件.由于产品质量好,款式受欢迎,前几个月的产品销售情况良好.为了使推销员在推销产品时,接受订单不至于过多或过少,需要估测以后几个月的产量.以这四个月的产品数据为依据,用一个函数模拟产品的月产量y与月份x的关系,模拟函数有三个备选:①一次函数f(x)=kx+b(k≠0),②二次函数g(x)=ax2+bx+c(a,b,c为常数,a≠0),③指数型函数m(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1).厂里分析,产量的增加是由于工人生产熟练和理顺了生产流程.厂里也暂时不准备增加设备和工人,假如你是厂长,将会采用什么办法估计以后几个月的产量?
16.土豆学名马铃薯,与稻、麦、玉米、高粱一起被称为全球五大农作物.云南人爱吃土豆,在云南土豆也称洋芋,昆明人常说“吃洋芋,长子弟”.年月,在全国两会的代表通道里,云南农业大学名誉校长朱有勇院士,举着一个两公斤的土豆,向全国的媒体展示,为来自家乡的“山货”代言,他自豪地说:“北京人吃的醋溜土豆丝,盘里有盘是我们澜沧种的!”
(1)在菜市上,听到小王叫卖:“洋芋便宜卖了,两元一斤,三元两斤,四元三斤,五元四斤,六元五斤,快来买啊!”结果一群人都在买六元五斤的.由此得到如下结论:一次购买的斤数越多,单价越低,请建立一个函数模型,来说明以上结论;
(2)小王卖洋芋赚到了钱,想进行某个项目的投资,约定如下:①投资金额固定;②投资年数可自由选择,但最短年,最长不超过年;③投资年数与总回报的关系,可选择下述三种方案中的一种:方案一:当时, ,以后每增加时,增加;方案二:;方案三:.请你根据以上材料,结合你的分析,为小王提供一个最佳投资方案.
参考答案
1.D
【解析】设比例系数为k,则电流强度I=kr3,
由已知可得当r=4时,I=320,
故有320=43k,解得k==5,
所以I=5r3,
则当r=3时,I=5×33=135(安).
故选:.
2.C
【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图象一定是下降的,由此排除A;
再由小明骑车上学,开始时匀速行驶可得出图象开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图象与x轴平行,由此排除D,
之后为了赶时间加快速度行驶,此一段时间段内函数图象下降的比较快,由此可确定C正确,B不正确.
故选C.
3.D
【解析】根据实验数据可以得出,近似增加一个单位时,的增量近似为2.5,3.5,4.5,6,比较接近,故选D.
4.D
【解析】根据基本初等函数的图象与性质可知,一次函数增长的速度不变,不满足题意;要满足调整后初期利润增长迅速,如果是二次函数,则必须开口向上,而此时在二次函数对称轴的右侧增长的速度是越来越快,没有慢下来的可能,不符合要求;要满足调整后初期利润增长迅速,如果是指数函数,则底数必是大于1的数,而此时指数函数增长的速度也是越来越快的,也不满足要求;对于对数函数,当底数大于1时,对数函数增长的速度先快后慢,符合要求,故选D.
5.A
【解析】两颗星的星等与亮度满足,令,
.
故选A.
6.A
【解析】因为2、4是函数的零点,所以排除B、C;
因为时,所以排除D,故选A
7.A
【解析】
故函数在上是减函数
则
故选
8.C
【解析】画出三个函数的图像如下图,由图像可知选C.因为三个函数都是下凸函数.
故选:C.
9.
【解析】,,
其中一次函数比对数函数在上增长较快.
故答案为:.
10.②④
【解析】由图像可知前5min中温度增加,但是增加速度越来越慢,所以②对,①错.5min以后温度图像是一条水平线,所以温度保持不变,④对,③错,选②④.
11.①③
【解析】
根据题意,函数的图象经过点,故函数为
令时,,故①正确;
令时,,减少,当时,减少,每月减少有害物质质量不相等,故②不正确;
分别令,解得 t1+t2=t3故③正确;
答案:①③.
12.
【解析】根据对数函数的定义可得,解得,因为二次函数图象的对称轴为,由复合函数单调性可得函数的单调递增区间为,要使函数在区间内单调递增,只需,解关于的不等式组得,即的取值范围是,故答案为.
13.(1)图象见解析,y=0.6777x+8.2067;(2)8.8844(万亿元),9.5621(万亿元);与实际的生产总值相比,误差不超过0.1万亿元;(3)19.7276万亿元.
【解析】(1)画出函数图象,如图所示.
从函数的图象可以看出,画出的点近似地落在一条直线上,设所求的函数关系式为y=kx+b(k≠0).
把直线经过的两点(0,8.206 7)和(3,10.239 8)代入上式,
解得k=0.677 7,b=8.206 7.∴函数关系式为y=0.677 7x+8.206 7.
(2)由得到的函数关系式计算出2017年和2018年的国内生产总值分别为
0.677 7×1+8.206 7=8.884 4(万亿元),
0.677 7×2+8.206 7=9.562 1(万亿元).
与实际的生产总值相比,误差不超过0.1万亿元.
(3)2033年,即x=17时,由(1)得y=0.677 7×17+8.206 7=19.727 6,
即预测2033年该国的国内生产总值约为19.727 6万亿元.
14.1.875万辆.
【解析】由已知得解得则y=-x-4+2,
当x=7时,y=-3+2=1.875.
故该品牌汽车7月的产量为1.875万辆.
15.选用m(x)=-0.8×0.5x+1.4来估计.
【解析】将已知前四个月的月产量y与月份x的关系记为A(1,1),B(2,1.2),C(3,1.3),D(4,1.37).
①对于一次函数f(x)=kx+b(k≠0),将B,C两点的坐标代入,有f(2)=2k+b=1.2,f(3)=3k+b=1.3,
解得k=0.1,b=1,故f(x)=0.1x+1.
所以f(1)=1.1,与实际误差为0.1,f(4)=1.4,与实际误差为0.03.
②对于二次函数g(x)=ax2+bx+c(a,b,c为常数,a≠0),将A,B,C三点的坐标代入,得
解得
故g(x)=-0.05x2+0.35x+0.7.
所以g(4)=-0.05×42+0.35×4+0.7=1.3,
与实际误差为0.07.
③对于指数型函数m(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1),将A,B,C三点的坐标代入,得
解得
故m(x)=-0.8×0.5x+1.4.
所以m(4)=-0.8×0.54+1.4=1.35,与实际误差为0.02.
比较上述3个模拟函数的优劣,既要考虑到剩余点的误差值最小,又要考虑生产的实际问题,比如增产的趋势和可能性,可以认为m(x)最佳,一是误差值最小,二是由于新建厂,开始随着工人技术、管理效益逐渐提高,一段时间内产量明显上升,但到一定时期后,设备不更新,那么产量必然要趋于稳定,而m(x)恰好反映了这种趋势,因此选用m(x)=-0.8×0.5x+1.4来估计以后几个月的产量比较接近客观实际.
16.(1);(2)答案见解析.
【解析】(1)设顾客一次购买斤土豆,每斤土豆的单价为元,
由题意知:,
因为,所以在为单调递减函数.
说明一次购买的斤数越多,单价越低;
(2)根据题意,按照年数的不同取值范围,选出总回报最高的方案.
由题意可知方案一对应的解析式为:.
列表得出三种方案所有年数的总回报,可以精确得出任意年数三种方案对应总回报的大小关系,进而可得出如下结论:
投资年数 总回报
方案一
方案二
方案三
当投资年数为年时,选择方案一最佳;
当投资年数为年时,选择方案一或方案二最佳;
当投资年数为年或年时,选择方案二最佳;
当投资年数为年时,选择方案二或方案三最佳;
当投资年数为年时,选择方案三最佳.
一、单选题
1.在固定电压差(电压为常数)的前提下,当电流通过圆柱形的电线时,其电流强度I(单位:安)与电线半径r(单位:毫米)的三次方成正比.若已知电流通过半径为4毫米的电线时,电流强度为320安,则电流通过半径为3毫米的电线时,电流强度为( )
A.60安 B.240安 C.75安 D.135安
2.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
3.某学校开展研究性学习活动,某同学获得一组实验数据如下表:
x 3 4
y 12
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是
A. B. C. D.
4.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润与时间的关系,可选用
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
5.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
6.函数的图象大致是
A.B.C. D.
7.已知,则
A. B.
C. D.
8.下面对函数与 在区间上的衰减情况说法正确的是( )
A.衰减速度越来越慢,衰减速度越来越快,衰减速度越来越慢
B.衰减速度越来越快,衰减速度越来越慢,衰减速度越来越快
C.衰减速度越来越慢,衰减速度越来越慢,衰减速度越来越慢
D.衰减速度越来越快,衰减速度越来越快,衰减速度越来越快
二、填空题
9.函数与函数在区间上增长较快的一个是________.
10.在某种金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示.
现给出下列说法:
①前5min温度增加的速度越来越快;②前5min温度增加的速度越来越慢;③5min以后温度保持匀速增加;④5min以后温度保持不变.
其中正确的说法是________.(填序号)
11.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图象.有以下叙述:
①第4个月时,剩留量就会低于;
②每月减少的有害物质量都相等;
③若剩留量为,,时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确叙述的序号是________.
12.若函数在区间内单调递增,则实数的取值范围为___.
三、解答题
13.某国2016年至2019年国内生产总值(单位:万亿元)如下表所示:
年份 2016 2017 2018 2019
x(年份代码) 0 1 2 3
生产总值y(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
(1)画出函数图象,猜想y与x之间的函数关系,近似地写出一个函数关系式;
(2)利用得出的关系式求生产总值,与表中实际生产总值比较;
(3)利用关系式预测2033年该国的国内生产总值.
14.某品牌汽车的月产能y(万辆)与月份x(3<x≤12且x∈N)满足关系式.现已知该品牌汽车今年4月、5月的产能分别为1万辆和1.5万辆,求该品牌汽车7月的产能为多少万辆.
15.某鞋厂从今年1月份开始投产,并且前四个月的产量分别为1万件、1.2万件、1.3万件、1.37万件.由于产品质量好,款式受欢迎,前几个月的产品销售情况良好.为了使推销员在推销产品时,接受订单不至于过多或过少,需要估测以后几个月的产量.以这四个月的产品数据为依据,用一个函数模拟产品的月产量y与月份x的关系,模拟函数有三个备选:①一次函数f(x)=kx+b(k≠0),②二次函数g(x)=ax2+bx+c(a,b,c为常数,a≠0),③指数型函数m(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1).厂里分析,产量的增加是由于工人生产熟练和理顺了生产流程.厂里也暂时不准备增加设备和工人,假如你是厂长,将会采用什么办法估计以后几个月的产量?
16.土豆学名马铃薯,与稻、麦、玉米、高粱一起被称为全球五大农作物.云南人爱吃土豆,在云南土豆也称洋芋,昆明人常说“吃洋芋,长子弟”.年月,在全国两会的代表通道里,云南农业大学名誉校长朱有勇院士,举着一个两公斤的土豆,向全国的媒体展示,为来自家乡的“山货”代言,他自豪地说:“北京人吃的醋溜土豆丝,盘里有盘是我们澜沧种的!”
(1)在菜市上,听到小王叫卖:“洋芋便宜卖了,两元一斤,三元两斤,四元三斤,五元四斤,六元五斤,快来买啊!”结果一群人都在买六元五斤的.由此得到如下结论:一次购买的斤数越多,单价越低,请建立一个函数模型,来说明以上结论;
(2)小王卖洋芋赚到了钱,想进行某个项目的投资,约定如下:①投资金额固定;②投资年数可自由选择,但最短年,最长不超过年;③投资年数与总回报的关系,可选择下述三种方案中的一种:方案一:当时, ,以后每增加时,增加;方案二:;方案三:.请你根据以上材料,结合你的分析,为小王提供一个最佳投资方案.
参考答案
1.D
【解析】设比例系数为k,则电流强度I=kr3,
由已知可得当r=4时,I=320,
故有320=43k,解得k==5,
所以I=5r3,
则当r=3时,I=5×33=135(安).
故选:.
2.C
【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图象一定是下降的,由此排除A;
再由小明骑车上学,开始时匀速行驶可得出图象开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图象与x轴平行,由此排除D,
之后为了赶时间加快速度行驶,此一段时间段内函数图象下降的比较快,由此可确定C正确,B不正确.
故选C.
3.D
【解析】根据实验数据可以得出,近似增加一个单位时,的增量近似为2.5,3.5,4.5,6,比较接近,故选D.
4.D
【解析】根据基本初等函数的图象与性质可知,一次函数增长的速度不变,不满足题意;要满足调整后初期利润增长迅速,如果是二次函数,则必须开口向上,而此时在二次函数对称轴的右侧增长的速度是越来越快,没有慢下来的可能,不符合要求;要满足调整后初期利润增长迅速,如果是指数函数,则底数必是大于1的数,而此时指数函数增长的速度也是越来越快的,也不满足要求;对于对数函数,当底数大于1时,对数函数增长的速度先快后慢,符合要求,故选D.
5.A
【解析】两颗星的星等与亮度满足,令,
.
故选A.
6.A
【解析】因为2、4是函数的零点,所以排除B、C;
因为时,所以排除D,故选A
7.A
【解析】
故函数在上是减函数
则
故选
8.C
【解析】画出三个函数的图像如下图,由图像可知选C.因为三个函数都是下凸函数.
故选:C.
9.
【解析】,,
其中一次函数比对数函数在上增长较快.
故答案为:.
10.②④
【解析】由图像可知前5min中温度增加,但是增加速度越来越慢,所以②对,①错.5min以后温度图像是一条水平线,所以温度保持不变,④对,③错,选②④.
11.①③
【解析】
根据题意,函数的图象经过点,故函数为
令时,,故①正确;
令时,,减少,当时,减少,每月减少有害物质质量不相等,故②不正确;
分别令,解得 t1+t2=t3故③正确;
答案:①③.
12.
【解析】根据对数函数的定义可得,解得,因为二次函数图象的对称轴为,由复合函数单调性可得函数的单调递增区间为,要使函数在区间内单调递增,只需,解关于的不等式组得,即的取值范围是,故答案为.
13.(1)图象见解析,y=0.6777x+8.2067;(2)8.8844(万亿元),9.5621(万亿元);与实际的生产总值相比,误差不超过0.1万亿元;(3)19.7276万亿元.
【解析】(1)画出函数图象,如图所示.
从函数的图象可以看出,画出的点近似地落在一条直线上,设所求的函数关系式为y=kx+b(k≠0).
把直线经过的两点(0,8.206 7)和(3,10.239 8)代入上式,
解得k=0.677 7,b=8.206 7.∴函数关系式为y=0.677 7x+8.206 7.
(2)由得到的函数关系式计算出2017年和2018年的国内生产总值分别为
0.677 7×1+8.206 7=8.884 4(万亿元),
0.677 7×2+8.206 7=9.562 1(万亿元).
与实际的生产总值相比,误差不超过0.1万亿元.
(3)2033年,即x=17时,由(1)得y=0.677 7×17+8.206 7=19.727 6,
即预测2033年该国的国内生产总值约为19.727 6万亿元.
14.1.875万辆.
【解析】由已知得解得则y=-x-4+2,
当x=7时,y=-3+2=1.875.
故该品牌汽车7月的产量为1.875万辆.
15.选用m(x)=-0.8×0.5x+1.4来估计.
【解析】将已知前四个月的月产量y与月份x的关系记为A(1,1),B(2,1.2),C(3,1.3),D(4,1.37).
①对于一次函数f(x)=kx+b(k≠0),将B,C两点的坐标代入,有f(2)=2k+b=1.2,f(3)=3k+b=1.3,
解得k=0.1,b=1,故f(x)=0.1x+1.
所以f(1)=1.1,与实际误差为0.1,f(4)=1.4,与实际误差为0.03.
②对于二次函数g(x)=ax2+bx+c(a,b,c为常数,a≠0),将A,B,C三点的坐标代入,得
解得
故g(x)=-0.05x2+0.35x+0.7.
所以g(4)=-0.05×42+0.35×4+0.7=1.3,
与实际误差为0.07.
③对于指数型函数m(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1),将A,B,C三点的坐标代入,得
解得
故m(x)=-0.8×0.5x+1.4.
所以m(4)=-0.8×0.54+1.4=1.35,与实际误差为0.02.
比较上述3个模拟函数的优劣,既要考虑到剩余点的误差值最小,又要考虑生产的实际问题,比如增产的趋势和可能性,可以认为m(x)最佳,一是误差值最小,二是由于新建厂,开始随着工人技术、管理效益逐渐提高,一段时间内产量明显上升,但到一定时期后,设备不更新,那么产量必然要趋于稳定,而m(x)恰好反映了这种趋势,因此选用m(x)=-0.8×0.5x+1.4来估计以后几个月的产量比较接近客观实际.
16.(1);(2)答案见解析.
【解析】(1)设顾客一次购买斤土豆,每斤土豆的单价为元,
由题意知:,
因为,所以在为单调递减函数.
说明一次购买的斤数越多,单价越低;
(2)根据题意,按照年数的不同取值范围,选出总回报最高的方案.
由题意可知方案一对应的解析式为:.
列表得出三种方案所有年数的总回报,可以精确得出任意年数三种方案对应总回报的大小关系,进而可得出如下结论:
投资年数 总回报
方案一
方案二
方案三
当投资年数为年时,选择方案一最佳;
当投资年数为年时,选择方案一或方案二最佳;
当投资年数为年或年时,选择方案二最佳;
当投资年数为年时,选择方案二或方案三最佳;
当投资年数为年时,选择方案三最佳.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
