2021—2022学年冀教版数学八年级上册 13.3 全等三角形的判定SAS 课件(22张ppt)
文档属性
| 名称 | 2021—2022学年冀教版数学八年级上册 13.3 全等三角形的判定SAS 课件(22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 16:57:49 | ||
图片预览







文档简介
(共21张PPT)
13.3全等三角形的判定
第2课时
——边角边
学习目标
1.理解和掌握全等三角形判定的基本事实“边角边”.
2.能灵活运用“边角边”证明三角形全等.
3.在探究的过程中提高观察、分析、归纳、合作的能力,体验主动探究问题的乐趣与成功的喜悦。
设置问题:
如果两个三角形有两条边和一个角分别对应相等,这两个三角形一定全等吗?此时应该有几种情况
一,画一个三角形ABC,使它的一个内角∠A=45°,夹这个角的两边AB=10cm,AC=8cm,
画法:
1.画一条线段AB=10cm
1.画∠MAB=45°
3.在射线AM上取AC=8cm
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(1)边角边
2.画一个△ABC,使它的一个内角∠A=45°这个角的邻边AC=10cm,这个角的对边BC=8cm,
画法:1.画∠MAN=45°
2.在AN上取AC=10cm
3.以点C为圆心,8cm为半径画弧交AM于点B,
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(2)边边角
A
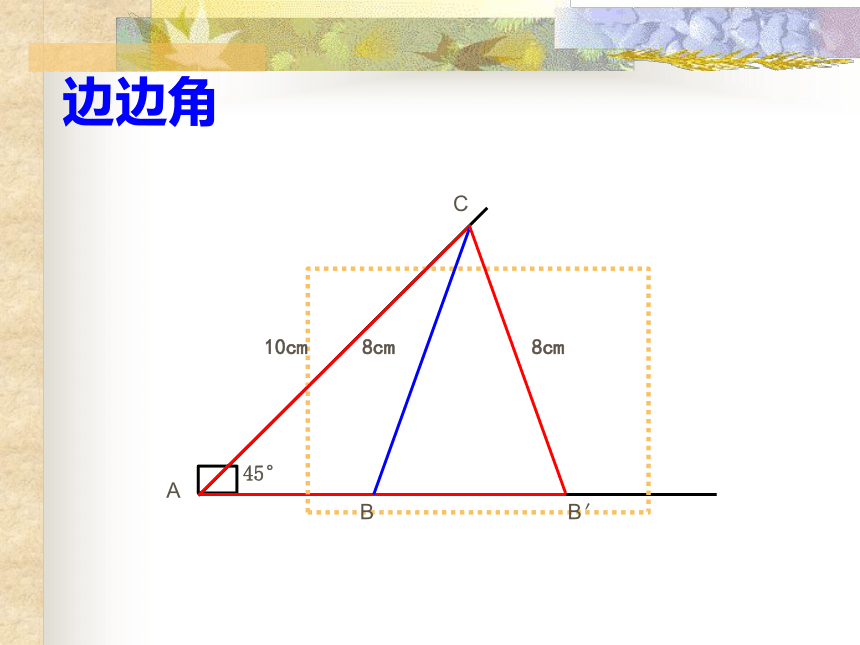
45°
边边角
B
B′
C
10cm
8cm
8cm
10cm
A
B′
C
45°
8cm
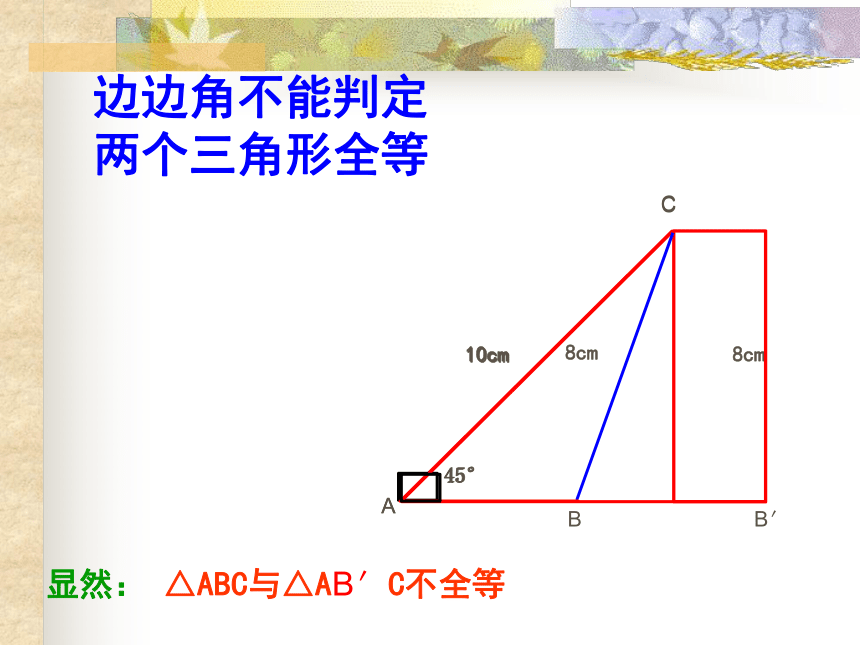
边边角不能判定
两个三角形全等
B
A
8cm
45°
10cm
C
显然: △ABC与△AB′C不全等
结论:基本事实二
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等。(简记为 “边角边”或SAS)。
注:“边边角”不能判定两个三角形全等
A
B
C
D
E
F
你会找夹角吗?
1.AC 与AB的夹角是_______ ,夹∠B的两条边是________
AB与BC的夹角是__________ ,夹∠C的两条边是_______
2.DF与DE的夹角是________,夹∠E的两条边是________
DE与EF的的夹角是__________,夹∠F的两条边是________
∠A
AB和BC
∠B
AC和BC
∠D
∠E
DE和EF
DF和EF
A
B
C
D
E
F
用数学符号语言表示边角边:
在△ABC和△ DEF中
AB=DE(已知)
__________
__________
∴ △________ ≌△ _______( )
∠B =∠E
BC=EF
ABC
DEF
SAS
AB=DE(已知)
__________
__________
∠A =∠D
AC=DE
新知应用:
1.在下列推理中填写需要补充的条件,使结论成立
在△AOB和△DOC中
A0=DO(已知)
=
(对顶角相等)
BO=CO(已知)
∴ △AOB≌△DOC( ).
A
B
O
D
C
∠AOB
∠DOC
SAS
(已知)
=
∠A=∠A(公共角)
=
A
D
C
B
E
∴△AEC ≌△ADB ( ).
2.在△AEC和△ADB中
AC
AB
AD
AE
SAS
注意:SAS中的角必须是两边的夹角,“A”必须在中间。
已知如图,AB=AD,∠BAC=∠DAC,求证△ABC≌△ADC
例题1:
证明: 在△ABC和△ ADC中
AB=AD(已知)
∠BAC=∠DAC(已知)
AC=AC(公共边)
∴ △ABC ≌△ADC( SAS )
变式1:
已知如图,AB=AD,AC平分∠BAD ,求证△ABC≌△ADC
变式2:(小组合作)
已知如图,AB=AD,AC平分∠BAD , 求证BC=DC
解题思路2:要证明两个三角形中的边相等,只需证明两个三角形全等。
例2:
已知如图:AD//BC,AD=CB,求证:△ADC≌△CBA
通过这节课的学习,你有什么收获?
课堂测试:
已知如图;AO=DO , BO=CO 求证:△AOB ≌ △DOC
证明:在 中
△AOB ≌ △DOC( )
________________
________________
________________
在△AOB和△ DOC
AO=DO(已知)
∠AOB=∠DOC(对顶角相等)
BO=CO(已知 )
∴
SAS
课下思考:
1.已知如图:点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=FE, ∠A=∠DFE,AF=DC.求证:△ABC ≌△FED
课后作业:
课本43页:练习1,2,3题
A组1,2,3
课本44页:B组1,2
13.3全等三角形的判定
第2课时
——边角边
学习目标
1.理解和掌握全等三角形判定的基本事实“边角边”.
2.能灵活运用“边角边”证明三角形全等.
3.在探究的过程中提高观察、分析、归纳、合作的能力,体验主动探究问题的乐趣与成功的喜悦。
设置问题:
如果两个三角形有两条边和一个角分别对应相等,这两个三角形一定全等吗?此时应该有几种情况
一,画一个三角形ABC,使它的一个内角∠A=45°,夹这个角的两边AB=10cm,AC=8cm,
画法:
1.画一条线段AB=10cm
1.画∠MAB=45°
3.在射线AM上取AC=8cm
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(1)边角边
2.画一个△ABC,使它的一个内角∠A=45°这个角的邻边AC=10cm,这个角的对边BC=8cm,
画法:1.画∠MAN=45°
2.在AN上取AC=10cm
3.以点C为圆心,8cm为半径画弧交AM于点B,
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(2)边边角
A
45°
边边角
B
B′
C
10cm
8cm
8cm
10cm
A
B′
C
45°
8cm
边边角不能判定
两个三角形全等
B
A
8cm
45°
10cm
C
显然: △ABC与△AB′C不全等
结论:基本事实二
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等。(简记为 “边角边”或SAS)。
注:“边边角”不能判定两个三角形全等
A
B
C
D
E
F
你会找夹角吗?
1.AC 与AB的夹角是_______ ,夹∠B的两条边是________
AB与BC的夹角是__________ ,夹∠C的两条边是_______
2.DF与DE的夹角是________,夹∠E的两条边是________
DE与EF的的夹角是__________,夹∠F的两条边是________
∠A
AB和BC
∠B
AC和BC
∠D
∠E
DE和EF
DF和EF
A
B
C
D
E
F
用数学符号语言表示边角边:
在△ABC和△ DEF中
AB=DE(已知)
__________
__________
∴ △________ ≌△ _______( )
∠B =∠E
BC=EF
ABC
DEF
SAS
AB=DE(已知)
__________
__________
∠A =∠D
AC=DE
新知应用:
1.在下列推理中填写需要补充的条件,使结论成立
在△AOB和△DOC中
A0=DO(已知)
=
(对顶角相等)
BO=CO(已知)
∴ △AOB≌△DOC( ).
A
B
O
D
C
∠AOB
∠DOC
SAS
(已知)
=
∠A=∠A(公共角)
=
A
D
C
B
E
∴△AEC ≌△ADB ( ).
2.在△AEC和△ADB中
AC
AB
AD
AE
SAS
注意:SAS中的角必须是两边的夹角,“A”必须在中间。
已知如图,AB=AD,∠BAC=∠DAC,求证△ABC≌△ADC
例题1:
证明: 在△ABC和△ ADC中
AB=AD(已知)
∠BAC=∠DAC(已知)
AC=AC(公共边)
∴ △ABC ≌△ADC( SAS )
变式1:
已知如图,AB=AD,AC平分∠BAD ,求证△ABC≌△ADC
变式2:(小组合作)
已知如图,AB=AD,AC平分∠BAD , 求证BC=DC
解题思路2:要证明两个三角形中的边相等,只需证明两个三角形全等。
例2:
已知如图:AD//BC,AD=CB,求证:△ADC≌△CBA
通过这节课的学习,你有什么收获?
课堂测试:
已知如图;AO=DO , BO=CO 求证:△AOB ≌ △DOC
证明:在 中
△AOB ≌ △DOC( )
________________
________________
________________
在△AOB和△ DOC
AO=DO(已知)
∠AOB=∠DOC(对顶角相等)
BO=CO(已知 )
∴
SAS
课下思考:
1.已知如图:点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=FE, ∠A=∠DFE,AF=DC.求证:△ABC ≌△FED
课后作业:
课本43页:练习1,2,3题
A组1,2,3
课本44页:B组1,2
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
