人教版 数学六年级下册 《圆锥的体积》(教案)
文档属性
| 名称 | 人教版 数学六年级下册 《圆锥的体积》(教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 444.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 12:14:51 | ||
图片预览


文档简介
《圆锥的体积》教学设计
教学目标:
1、 通过动手操作实验,推导出圆锥的体积的计算方法,并能运用公式计算圆锥的体积。
2、 通过学生动手、动脑,培养学生的思维能力和空间想象能力。
3、 培养学生个人的自主学习能力和小组的合作学习能力。
教学重点:圆锥的体积计算公式。
教学难点:圆锥的体积计算公式的推导过程。
教学关键:学生通过实验操作,理解“圆锥的体积等于与它等底等高的圆柱的体积的”。
教学准备:
1、准备若干同样的圆柱形容器,若干与圆柱等底等高的圆锥;若干水槽,若干小杯子,沙子和水;铅锤1个;量筒一个。
2、多媒体课件设计。
3、充分利用网络资源,本教学设计的资源主要来源于人民教育出版社,同方教育资源库和国家基础教育资源网。
教学方法及组织形式:
自主探究,合作交流的教学方法。
教学过程:
一、复习导入
师:同学们,我们已经学习过了哪些立体图形的体积计算?
生:我们学过了长方体、正方体、圆柱的体积计算。
师:那现在谁来回忆一下长方体的体积计算公式呢?
生1:长方体的体积=长×宽×高 用字母表示是: v=abh
师:正方体的体积计算公式,谁来说?
生2:正方体的体积=棱长×棱长×棱长 用字母表示是: v=a
师:圆柱体呢?
生3:圆柱体的体积=底面积×高 用字母表示是: v=sh
二、教学圆锥的体积公式的推导过程
(1) 引出问题。
师:很好。老师这里有一个铅锤,它是什么形状的?
生:圆锥。
师:你有办法知道这个铅锤的体积吗?
(学生讨论,然后汇报交流)。
生:我用排水法,把它放进盛水的量杯里,看水面升高多少,就是铅锤的体积。(同时上台演示给大家看)。
师:你们认为这样的方法好吗?
生:好。
师:如果有很多这样大小不一样的铅锤呢?
生:如果每个圆锥都这样测,太麻烦了!
师:那你有什么好的想法吗?
生:我们以前学过的体积都有计算公式,我想要是圆锥也有一个计算公式就好了。
(2) 联想、猜测。
师: 圆锥的体积可能和什么图形的体积有关,有什么关系?(引导学生将圆锥的体积与圆柱的体积联系起来。)
生:我认为圆锥的体积可能与圆柱的体积有关。
师:你是怎样想的呢?
生:因为圆柱的底面是圆,圆锥的底面也是圆,所以我认为它们一定有关系。(掌声鼓励)
同时课件出示图片
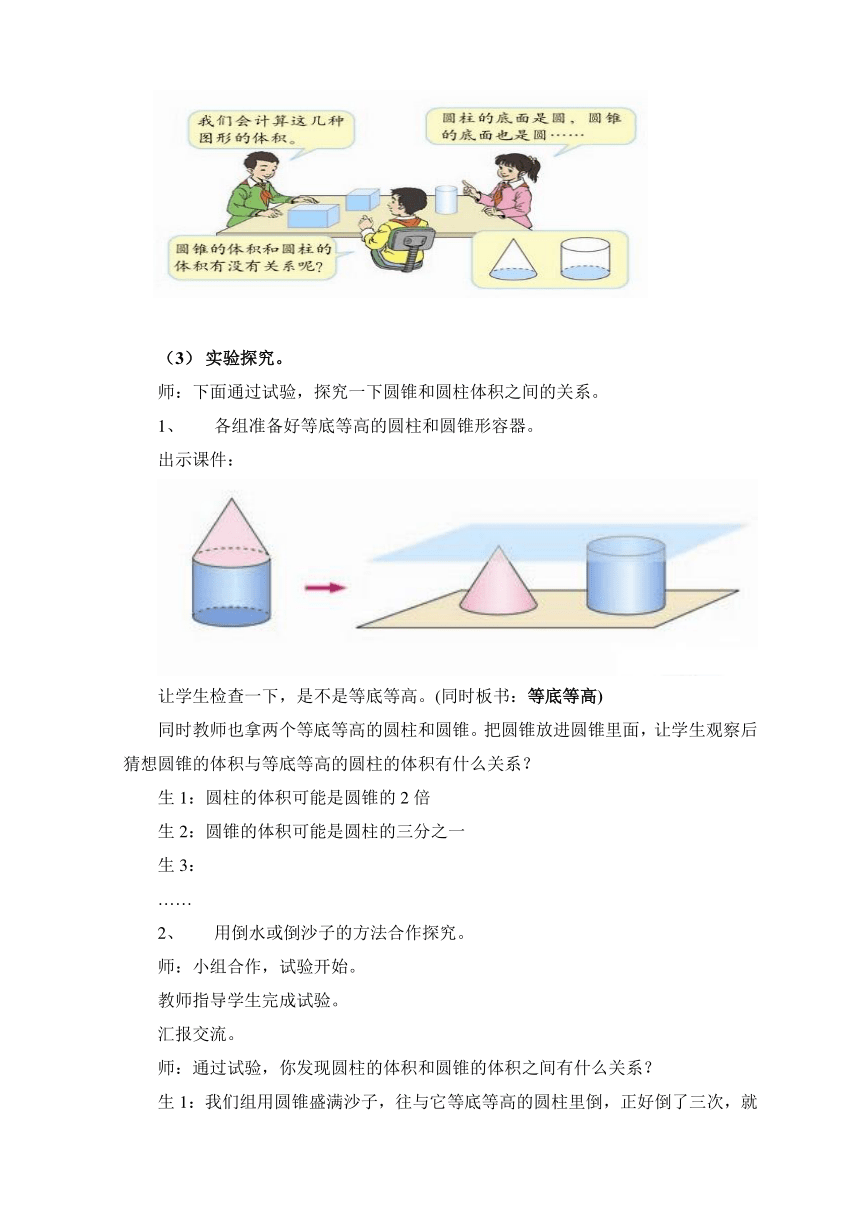
(3) 实验探究。
师:下面通过试验,探究一下圆锥和圆柱体积之间的关系。
1、 各组准备好等底等高的圆柱和圆锥形容器。
出示课件:
让学生检查一下,是不是等底等高。(同时板书:等底等高)
同时教师也拿两个等底等高的圆柱和圆锥。把圆锥放进圆锥里面,让学生观察后猜想圆锥的体积与等底等高的圆柱的体积有什么关系?
生1:圆柱的体积可能是圆锥的2倍
生2:圆锥的体积可能是圆柱的三分之一
生3:
……
2、 用倒水或倒沙子的方法合作探究。
师:小组合作,试验开始。
教师指导学生完成试验。
汇报交流。
师:通过试验,你发现圆柱的体积和圆锥的体积之间有什么关系?
生1:我们组用圆锥盛满沙子,往与它等底等高的圆柱里倒,正好倒了三次,就装满了。这说明圆柱的体积是与它等底等高的圆锥的3倍。
生2:我们组用圆柱盛满水,往与它等底等高的圆锥里倒了三次才倒完,这说明圆柱的体积是与它等底等高的圆锥的3倍。
生3:我们组用圆锥盛满水,往与它等底等高的圆柱里倒,正好倒了三次,就装满了。这说明圆锥的体积等于与它等底等高的圆柱的体积的。
……
(4) 师:刚才几个小组汇报得很好。为了让大家看得更清楚,现在老师用带有红色的水给大家现场演示一下:
(5) 导出公式。
师:通过试验,你发现等底等高的圆锥、圆柱的体积有什么关系?你能用字母表示出它们的关系吗?
生:圆柱的体积是与它等底等高的圆锥的体积的3倍,
圆锥的体积是与它等底等高的圆柱的体积的。
教师同时板书:
=
=Sh
师:刚才同学们通过自主的合作探究,得出了圆锥的计算公式,这就是我们今天要学习的内容——圆锥的体积。(教师点题,同时板书:圆锥的体积)
师:学习了这个内容,让我们去解决问题,请同学们把书翻到第27页。
课件出示
请生回答,说明理由。
三、教学圆锥的体积计算。
教师创设情景课件出示例3
师:告诉我们哪些已知条件?
生:圆锥形沙堆的底面直径是4m,高1.2m。
师:要求圆锥形沙堆的体积,必须先求什么?
生1:必须先用圆的面积公式S=πΥ求出底面积。
生2:要求底面积又必须先用“直径÷2”求出半径。
师:同学们,会求了吗?,要注意得数要保留两位小数。
开始做吧!谁愿意上来板演?(抽一人板演)
然后汇报交流。
师:为什么要乘?(加深对圆锥体积公式的理解,防止出现错误。)
最后教师用课件演示一次解答过程并点评。
四、巩固练习
(一)师:接下来,打开书第28页,第7题。(课件出示)
充分争论,抽生回答,并讲明道理。1题是错的,要等底等高。2题是对的,3题是错的,因为没有说是等底。
(二)师:第28页的第8题。自己读题,独立完成。
课件出示题目:
师:这道题谁来汇报?
生:×3.14×1.5×1.1=2.5905(m)
2.5905×1.4=3.6267≈4(吨)
答:这堆煤的体积是2.5905 m,这堆煤约有4吨。
学生汇报的同时,课件演示解答过程。
5、 课堂小结
师:今天这节课我们学习了圆锥的体积,发现圆锥的体积等于与它等底等高的圆柱的体积的三分之一。用字母表示就是:
=
=Sh
并运用它能解决很多问题。
同学们,你们都学会了吗?今天这节课我们就学到这儿。再见!
另附1:板书设计
圆锥的体积
等底等高 =
=Sh
教学目标:
1、 通过动手操作实验,推导出圆锥的体积的计算方法,并能运用公式计算圆锥的体积。
2、 通过学生动手、动脑,培养学生的思维能力和空间想象能力。
3、 培养学生个人的自主学习能力和小组的合作学习能力。
教学重点:圆锥的体积计算公式。
教学难点:圆锥的体积计算公式的推导过程。
教学关键:学生通过实验操作,理解“圆锥的体积等于与它等底等高的圆柱的体积的”。
教学准备:
1、准备若干同样的圆柱形容器,若干与圆柱等底等高的圆锥;若干水槽,若干小杯子,沙子和水;铅锤1个;量筒一个。
2、多媒体课件设计。
3、充分利用网络资源,本教学设计的资源主要来源于人民教育出版社,同方教育资源库和国家基础教育资源网。
教学方法及组织形式:
自主探究,合作交流的教学方法。
教学过程:
一、复习导入
师:同学们,我们已经学习过了哪些立体图形的体积计算?
生:我们学过了长方体、正方体、圆柱的体积计算。
师:那现在谁来回忆一下长方体的体积计算公式呢?
生1:长方体的体积=长×宽×高 用字母表示是: v=abh
师:正方体的体积计算公式,谁来说?
生2:正方体的体积=棱长×棱长×棱长 用字母表示是: v=a
师:圆柱体呢?
生3:圆柱体的体积=底面积×高 用字母表示是: v=sh
二、教学圆锥的体积公式的推导过程
(1) 引出问题。
师:很好。老师这里有一个铅锤,它是什么形状的?
生:圆锥。
师:你有办法知道这个铅锤的体积吗?
(学生讨论,然后汇报交流)。
生:我用排水法,把它放进盛水的量杯里,看水面升高多少,就是铅锤的体积。(同时上台演示给大家看)。
师:你们认为这样的方法好吗?
生:好。
师:如果有很多这样大小不一样的铅锤呢?
生:如果每个圆锥都这样测,太麻烦了!
师:那你有什么好的想法吗?
生:我们以前学过的体积都有计算公式,我想要是圆锥也有一个计算公式就好了。
(2) 联想、猜测。
师: 圆锥的体积可能和什么图形的体积有关,有什么关系?(引导学生将圆锥的体积与圆柱的体积联系起来。)
生:我认为圆锥的体积可能与圆柱的体积有关。
师:你是怎样想的呢?
生:因为圆柱的底面是圆,圆锥的底面也是圆,所以我认为它们一定有关系。(掌声鼓励)
同时课件出示图片
(3) 实验探究。
师:下面通过试验,探究一下圆锥和圆柱体积之间的关系。
1、 各组准备好等底等高的圆柱和圆锥形容器。
出示课件:
让学生检查一下,是不是等底等高。(同时板书:等底等高)
同时教师也拿两个等底等高的圆柱和圆锥。把圆锥放进圆锥里面,让学生观察后猜想圆锥的体积与等底等高的圆柱的体积有什么关系?
生1:圆柱的体积可能是圆锥的2倍
生2:圆锥的体积可能是圆柱的三分之一
生3:
……
2、 用倒水或倒沙子的方法合作探究。
师:小组合作,试验开始。
教师指导学生完成试验。
汇报交流。
师:通过试验,你发现圆柱的体积和圆锥的体积之间有什么关系?
生1:我们组用圆锥盛满沙子,往与它等底等高的圆柱里倒,正好倒了三次,就装满了。这说明圆柱的体积是与它等底等高的圆锥的3倍。
生2:我们组用圆柱盛满水,往与它等底等高的圆锥里倒了三次才倒完,这说明圆柱的体积是与它等底等高的圆锥的3倍。
生3:我们组用圆锥盛满水,往与它等底等高的圆柱里倒,正好倒了三次,就装满了。这说明圆锥的体积等于与它等底等高的圆柱的体积的。
……
(4) 师:刚才几个小组汇报得很好。为了让大家看得更清楚,现在老师用带有红色的水给大家现场演示一下:
(5) 导出公式。
师:通过试验,你发现等底等高的圆锥、圆柱的体积有什么关系?你能用字母表示出它们的关系吗?
生:圆柱的体积是与它等底等高的圆锥的体积的3倍,
圆锥的体积是与它等底等高的圆柱的体积的。
教师同时板书:
=
=Sh
师:刚才同学们通过自主的合作探究,得出了圆锥的计算公式,这就是我们今天要学习的内容——圆锥的体积。(教师点题,同时板书:圆锥的体积)
师:学习了这个内容,让我们去解决问题,请同学们把书翻到第27页。
课件出示
请生回答,说明理由。
三、教学圆锥的体积计算。
教师创设情景课件出示例3
师:告诉我们哪些已知条件?
生:圆锥形沙堆的底面直径是4m,高1.2m。
师:要求圆锥形沙堆的体积,必须先求什么?
生1:必须先用圆的面积公式S=πΥ求出底面积。
生2:要求底面积又必须先用“直径÷2”求出半径。
师:同学们,会求了吗?,要注意得数要保留两位小数。
开始做吧!谁愿意上来板演?(抽一人板演)
然后汇报交流。
师:为什么要乘?(加深对圆锥体积公式的理解,防止出现错误。)
最后教师用课件演示一次解答过程并点评。
四、巩固练习
(一)师:接下来,打开书第28页,第7题。(课件出示)
充分争论,抽生回答,并讲明道理。1题是错的,要等底等高。2题是对的,3题是错的,因为没有说是等底。
(二)师:第28页的第8题。自己读题,独立完成。
课件出示题目:
师:这道题谁来汇报?
生:×3.14×1.5×1.1=2.5905(m)
2.5905×1.4=3.6267≈4(吨)
答:这堆煤的体积是2.5905 m,这堆煤约有4吨。
学生汇报的同时,课件演示解答过程。
5、 课堂小结
师:今天这节课我们学习了圆锥的体积,发现圆锥的体积等于与它等底等高的圆柱的体积的三分之一。用字母表示就是:
=
=Sh
并运用它能解决很多问题。
同学们,你们都学会了吗?今天这节课我们就学到这儿。再见!
另附1:板书设计
圆锥的体积
等底等高 =
=Sh
