人教版七下第五章相交线与平行线全章导学案
文档属性
| 名称 | 人教版七下第五章相交线与平行线全章导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 898.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-23 21:51:27 | ||
图片预览



文档简介
七年级数学(下)导学案
第五章相交线与平行线(一)— 相交线
学习目标:
1、经历观察、推理、交流等过程,了解邻补角和对顶角的概念,
2、掌握邻补角、对顶角的性质;
学习过程
环节一:复习引入
1、复习提问:若∠1和∠2互余,则________________
若∠1和∠2互补,则________________
2、画图:作直线AB、CD相交于点O
3、探究新知
两直线相交 所形成的角 分类 位置关系 大小关系
∠1和∠2 ,∠2和∠___∠__和∠__,∠__和∠__
∠1和∠3, ∠__和∠__
归纳:
有一条公共边,而且另一边互为反向延长线的两个角叫做互为________。如图中的______和_______
如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫做互为_________。如图中的_________和__________
3、想一想:如果改变∠1的大小, ∠1和∠2还是邻补角吗?_______,它们的大小关系是____________。∠1和∠3还是对顶角吗?_______,它们的大小关系是________
结论:从数量上看,邻补角__________,对顶角都_______________
环节二:例题
例:如图,直线a,b相交,∠1=400,求∠2,∠3,∠4的度数
解:∵直线a,b相交
∴∠1+∠2=1800(邻补角的定义)
∴ ∠2=__________________
=__________________
=__________
∵直线a,b相交
∴∠3=∠____=________
∠4=∠____=_________( )
环节三:练习
A组
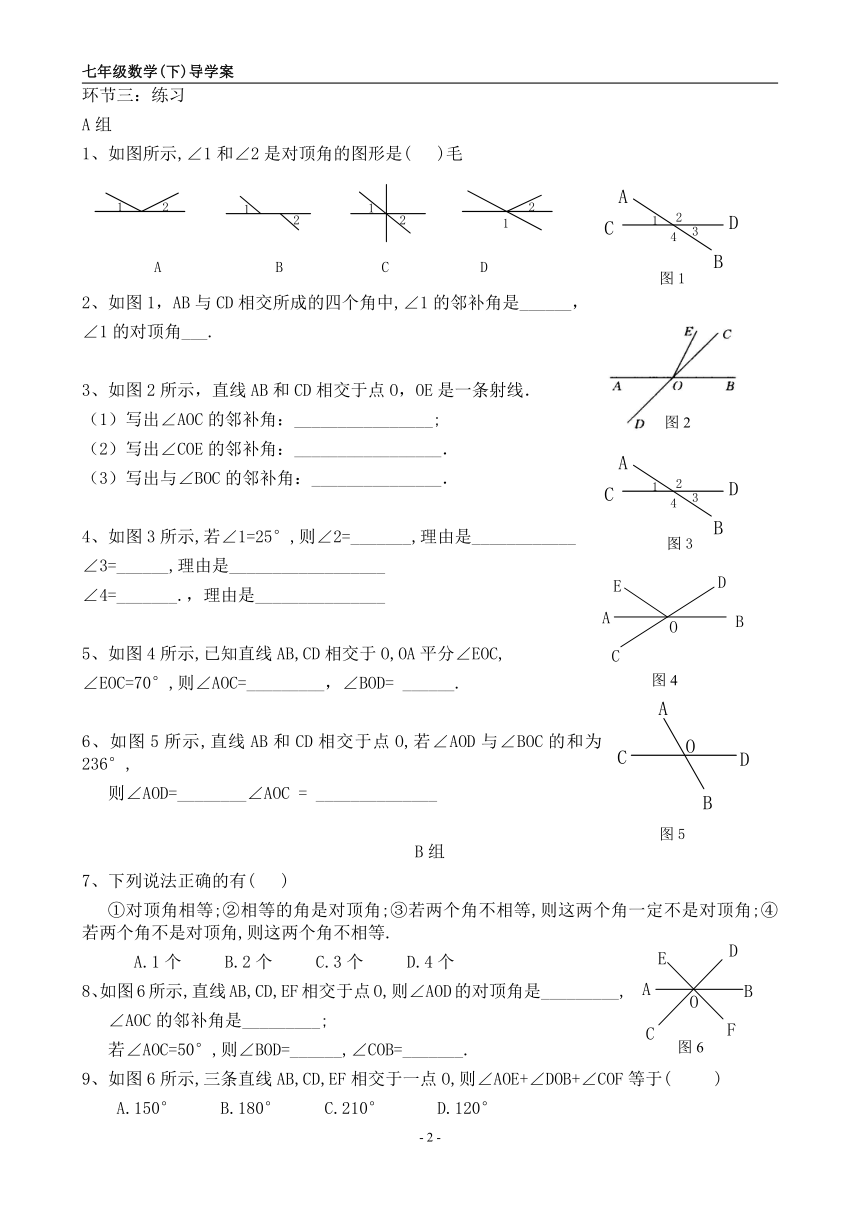
1、如图所示,∠1和∠2是对顶角的图形是( )毛
2、如图1,AB与CD相交所成的四个角中,∠1的邻补角是______,
∠1的对顶角___.
3、如图2所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:________________;
(2)写出∠COE的邻补角:_________________.
(3)写出与∠BOC的邻补角:_______________.
4、如图3所示,若∠1=25°,则∠2=_______,理由是____________
∠3=______,理由是__________________
∠4=_______.,理由是_______________
5、如图4所示,已知直线AB,CD相交于O,OA平分∠EOC,
∠EOC=70°,则∠AOC=_________,∠BOD=______.
6、如图5所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,
则∠AOD=________∠AOC= ______________
B组
7、下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
8、如图6所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,
∠AOC的邻补角是_________;
若∠AOC=50°,则∠BOD=______,∠COB=_______.
9、如图6所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
10、如图7,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
11、如图8,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,
求∠BOD,∠AOE的 度数.
C组
13、如图8所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,则∠EOD=________.
第五章相交线与平行线(二)—垂线
学习目标:
1、明确垂线的定义,并能过已知点画已知直线的垂线;明确垂线的性质;
2、能用简单的数学语言叙述图形的某些位置关系;
探究一:
1、画图:作直线AB、CD相交于点O。
2、画图:作直线AB、CD相交于点O,使∠AOD=90°,
回答:此时∠BOD= °,∠AOC= °,∠BOC= °
3、定义:
两直线AB、CD相交于点O,当所构成的四个角中有一个为 时,直线AB、CD互相垂直,交点O叫做 ,记作 ⊥ ,垂足为O。
探究二:垂线的画法:(可用三角板或量角器作图)
1、填表
如图,经过直线AB外一点P,画直线CD与已知直线AB垂直。 如图,经过直线AB上一点P,画直线CD与已知直线AB垂直。
2、小组讨论:
①组内是否有不同的画法?
②过点P作AB的垂线,这样的垂线有 条。
3、结论:
在同一平面内,经过直线外或直线上一点, 条直线与已知直线垂直。
探究三:
1.画图:已知直线l与直线外一点A
①过A作AO⊥l,垂足为O;
(我们称AO为点A到直线 的垂线段)
②在直线l上任取两点B、C;
③连结AB、AC;
2.用刻度尺度量得:AB= , AC= ,AO=
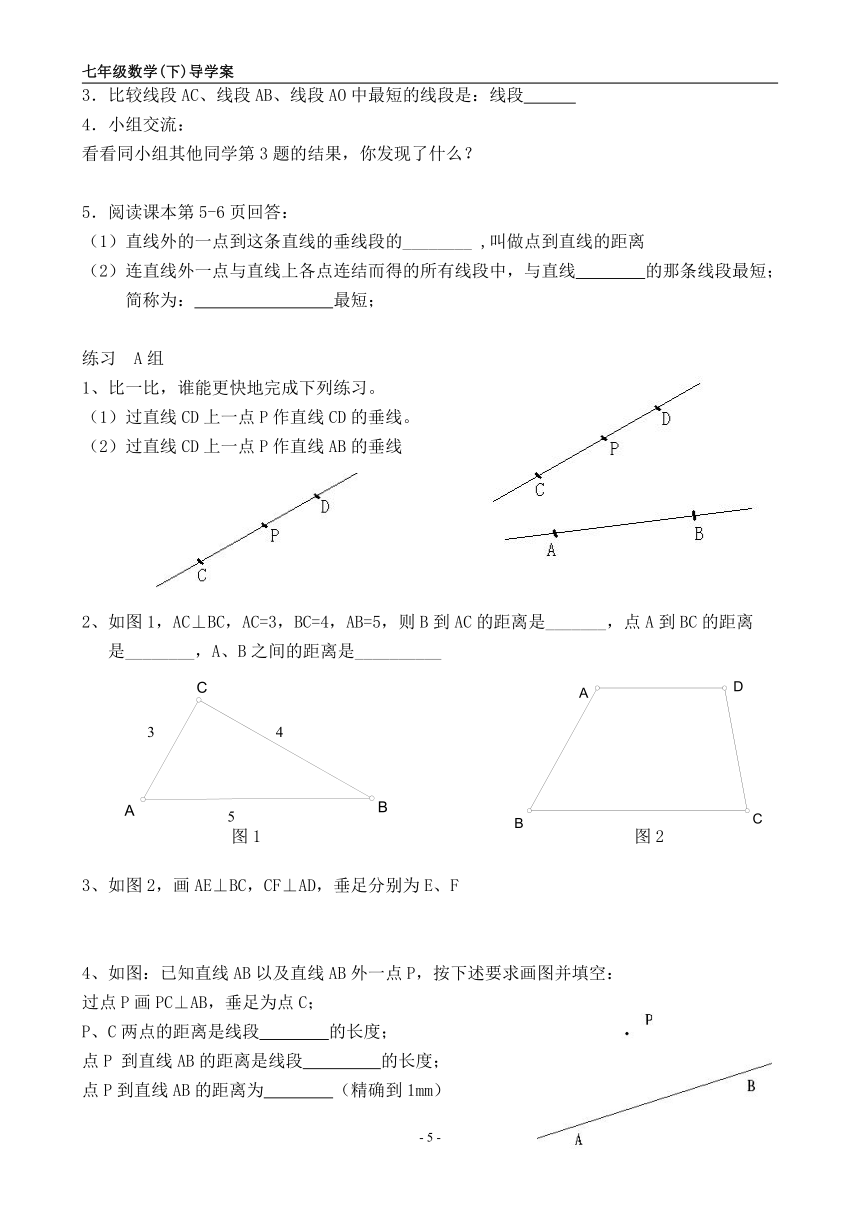
3.比较线段AC、线段AB、线段AO中最短的线段是:线段
4.小组交流:
看看同小组其他同学第3题的结果,你发现了什么?
5.阅读课本第5-6页回答:
(1)直线外的一点到这条直线的垂线段的________ ,叫做点到直线的距离
(2)连直线外一点与直线上各点连结而得的所有线段中,与直线 的那条线段最短;
简称为: 最短;
练习 A组
1、比一比,谁能更快地完成下列练习。
(1)过直线CD上一点P作直线CD的垂线。
(2)过直线CD上一点P作直线AB的垂线
2、如图1,AC⊥BC,AC=3,BC=4,AB=5,则B到AC的距离是_______,点A到BC的距离
是________,A、B之间的距离是__________
3、如图2,画AE⊥BC,CF⊥AD,垂足分别为E、F
4、如图:已知直线AB以及直线AB外一点P,按下述要求画图并填空:
过点P画PC⊥AB,垂足为点C;
P、C两点的距离是线段 的长度;
点P 到直线AB的距离是线段 的长度;
点P到直线AB的距离为 (精确到1mm)
5、画一条线段或射线的垂线,就是画它们所在直线的垂线,如图,请你过点P画出线段AB或射线AB的垂线
(1) (2) (3)
·P ·P
B 组
6、分别画出下列三个三角形中AB边上的高CD,并量出顶点C到AB的距离。
7、如图,在铁路(直线)旁有一村庄A,现在要建火车站,为方便该村庄的人乘车,
火车站应建在什么位置?请画图表示出来。
解:过点A作
火车站应建在 点处。
由是
第五章相交线与平行线(三)—相交线中的角
学习目标
1、明确什么是同位角、内错角、同旁内角
2、能正确找出图中的同位角、内错角、同旁内角
复习回顾:
两条直线相交,可得几个角,这些角有什么关系?
图 形 相等的角有 互补的角有
探索:
1、如图,已知直线AB、直线CD,画直线EF分别与AB、CD相交于点M、N,
问:图中共有_______个角,分别是__________________________________
A
2、填表:(观察以下的角与直线a、b、l位置关系,并填写下表)
表一:
∠2和∠6 位于直线a、b的___方,位于直线l的___侧
∠3和∠7 位于直线a、b的___方,位于直线l的___侧
∠1和∠5 位于直线a、b的___方,位于直线l的___侧
∠4和∠8 位于直线a、b的___方,位于直线l的___侧
像以上每一对角,都在直线l的同侧,直线a、b的上方,这样位置的一对角是 角。
表二:
∠3和∠5 位于直线a、b的_____,位于直线l的______
∠4和∠6 位于直线a、b的_____,位于直线l的______
像以上每一对角,都在直线l的_______,直线a、b_______,这样位置的角是________ 角;
表三:
∠3和∠6 位于直线a、b的______,位于直线l的______
∠4和∠5 位于直线a、b的______,位于直线l的______
像以上每一对角,都在直线l的_______,直线a、b_______,这样位置的角是 角;
练习 A组
1、如图,图中同位角有_____对,分别是
内错角有______对,分别是
同旁内角有_____对,分别是_________________
2、如图,与∠1是同位角的是_______________;
与∠2是内错角的是 ;
与∠1是同旁内角的是 __________________;
与∠2互为补角的是 ;
∠2的对顶角是 。
3、如图,∠1与∠D是________角;
∠1与∠B是________角;∠B和∠C
是________角,∠D和∠C是________角。
4、如图,与∠DAB是内错角是: ;
与∠EAC是内错角是: ;
与∠B是同旁内角的是: ____ ___.
B组
5、找出图中的内错角: ;
找出图中的同位角: ;
6、如图,找出图中∠1的内错角: _____
∠2的内错角:
7、如图,∠1和∠2是两条直线_________和__________被直线_________所截而成的_________角,∠3和∠4是两条直线________和________被直线________所截而成的_________角。
8、在图中画出一条直线,使图中出现∠AOD的同位角,
说明哪一个角是∠AOD的同位角,并画出图形;
解:图中,∠ 与∠AOD是同位角;
C 组
9、∠1是直线a、b相交所成的角,用量角器量出∠1的度数,画一条直线c,使得直线c与直线b相交所成的角中有一个与∠1相等.
第五章 相交线(四)----练习
知识点回顾:
1、对顶角、邻补角
如图,直线AB与直线CD交于点O,则∠1的
对顶角是_______,∠1的邻补角是_________
从数量上看,邻补角__________,对顶角______________
2、垂线
(1)如图1,∵AB⊥CD,垂足为O
∴__________________________
(2)如图1,∵∠BOC=900
∴____________________________
(3)在同一平面内,经过直线外或直线上一点,
条直线与已知直线垂直。
(4)连接直线外一点与直线上各点的所有线段中, 最短;
直线外的一点到这条直线的垂线段的________ ,叫做点到直线的距离
画图:过点P作直线CD⊥直线AB,垂足为O
·P
A B
则__________________叫做点P到直线AB的距离。
3、三线八角
如图,直线a、b被直线l所截,构成八个角,则
(1)∠1和∠5是___________,
类似的还有___________________________
(2)∠3和∠5是___________,
类似的还有___________________________
(3)∠4和∠5是___________,
类似的还有___________________________
练习: A组
1、如图1,直线AB、CD、EF相交于点O
(1)∠AOC的邻补角是________________
∠BOE的邻补角是__________________
(2)∠DOA的对顶角是_____________
∠EOC的对顶角是_____________
(3)如果∠AOC=500,
则∠BOD=_________,理由是______________________
∠COB=_________,理由是______________________
2、如图2,∠EOC的邻补角是_______,∠BOC的邻补角是_____________
3、如图3,若∠1=300,∠2=400,则∠3=________,∠4=_________,∠5=________
4、如图4,直线AB、CD相交于点O,且∠AOC+∠BOD=1200,则∠BOC=________
5、如图5,点O是直线AB上一点
(1)若OC⊥OD,∠AOC=350,则∠BOD=____________ ;
(2)若∠AOC=400,∠BOD=500,则∠COD=___________,OC________OD
6、如图6,若OC⊥AB,∠1=300,则∠2=____________
B 组
7、如7图,∠ABC的同位角是 :
∠ABC的内错角是 :
∠ABC的同旁内角是
8、如图8,∠AFD的同位角是 :
∠AFG的内错角是 :
∠BGF的同旁内角是
9、如图9, ∠AME的同位角是___ ____:
∠MNP的内错角是 _:
∠MOP的同旁内角是 _____
10、画过A作BC的垂线
11、如图,△ABC中,∠C=900,△ABC的三条边AB、BC、CA中,
最长的是_________,理由是___________________________
12、如右图:,图中共有______个直角, 线段________的长表示点C到AB的距离,线段________的长表示点A到BC的距离.
13、如图. 直线CD过点O,且,求的度数.
C组
14、如图,(1)用量角器画∠AOB的平分线OC,
(2)在OC上任取一点P,画出点P到OA的距离PM
(3)画出点P到OB的距离PN
(4)比较PM、PN的大小
第五章 相交线与平行线(五)—平行线及其公理
学习目标
1、感受平行线的概念,能作出已知直线的平行线。
2、了解平行线的公理及其推论。
学习过程
环节一:学习平行线的定义
1.填表:
用目测画二条直线,使它们互相平行 画二条不平行的直线
EMBED Equation.DSMT4
2、阅读课本第12页,回答:
平行线的定义:
3、我们如何用几何语言描述平行线?
直线AB与CD平行,记作 AB∥CD
直线m与n平行,记作
环节二:学行线有关的公理
1.填空:
①点A在直线外,经过点A作一直线
小组讨论:直线和的位置关系
和的第一种位置关系:
和的第二种位置关系:
思考:经过直线外一点有 条直线与已知直线平行?
②分别画二条与直线平行的直线和
观察你上面所画的图形,可知直线和之间的位置关系是:
2、与平行线有关的公理(要求记忆)
①平行公理:经过直线外一点,有且只有 条直线与这条直线平行.
②如果两条直线都与第三条直线平行,那么这两条直线也互相 。
几何语言:
∵b∥a, c∥a
∴ ∥
环节三:练习
A组:
1.两条直线相交,交点的个数是 个;两条直线平行,交点的个数是 个。
2.判断题:
(1)不相交的两条直线叫做平行线。( )
(2)如果一条直线与两条平行线中的一条直线平行,那么它与另一条直线也互相平行。( )
(3)过一点有且只有一条直线平行于已知直线。( )
3.一条直线与另两条平行直线的关系是( )
A.一定与两条平行线平行; B.可能与两条平行线的一条平行,一条相交;
C.一定与两条平行线相交; D.与两条平行线都平行或都相交。
4.在同一平面内的两条直线的位置关系可能有( )
A.两种:平行与相交 B.两种:平行与垂直
C.三种:平行、垂直与相交 D.两种:垂直与相交
5.下列表示方法正确的是( )
A.∥A B.AB∥A C.∥ D.∥
B 组:
6.同一平面内的三条直线,其交点的个数可能为 。
7.下列说法中,错误的是( )
A.如果⊥,⊥,那么∥; B.如果∥,∥,那么∥;
C.⊥,∥,那么⊥; D.有且只有一条直线与已知直线平行。
8.读下列语句并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
(2)直线AB,CD是相交线,点P是直线AB,CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E。
9、如图,直线a、b被直线l所截
(1)∠5的同位角是_______,∠5的内错角是_______,∠5的同旁内角是________
(2)如果∠5=∠3,那么∠5与∠1有何关系?为什么?
(3)如果∠5+∠4=1800,那么∠5与∠1有何关系?
为什么?
C 组:
如图,梯形ABCD中AB∥CD,连接DB,过C画DB的平行线与AB的延长线交于F,并度量DC与BF的长度,比较DB与CF的大小。
第五章相交线与平行线(六)—平行线的判定(1)
学习目标
1、感受平行线判定方法的推导过程,了解并掌握三种判定方法。
2、能灵活运用平行线的判定方法进行解题。
学习过程
环节一:学习用三角板推平行线
1、先看教师示范用一块三角板借助黑板的一边作出一组平行线。
2、每人尝试借助两块三角板作一条直线与已知直线平行。然后画一条直线与a、b相交;
环节二:学习平行线的识别。
1、(1)观察图(一)∠1和∠2________角,由作图过程可知∠1和∠2的大小关系是__________,此时直线a和b_______________
(2)思考:在图(二)中标出一对同位角∠3和∠4,
那么它们的大小关系是______
(3)结论:同位角 ,两直线平行。
几何表示:如图
∵∠1=∠2
∴a//b(__________________,两直线平行)
2、如图,∠2和∠3是______角,当∠2=∠3时,直线a和b的位置关系是:______
理由:
3、如图,∠2和∠4是______角,当它们满足:__________时,a//b
理由:
4、结论:内错角 ,两直线平行。
同旁内角 ,两直线平行。
5、几何语言表示平行线的识别方法:(要求记忆)
(1) 同位角相等,两直线平行
∵∠1=∠2
∴ ∥ (同位角______,两直线平行)
(2)内错角相等,两直线平行
∵∠3=∠2
∴ ∥ ( 内错角______,两直线平行)
(3)同旁内角互补,两直线平行
∵∠4+∠2=180°
∴ ∥ ( 同旁内角_______,两直线平行)
环节三:练习 A组
1.如图(1),
若∠1=∠2,则
2.如图(2)
如果∠1=∠A,那么 ∥ ;
如果∠1=∠F,那么 ∥ ;
如果∠FDA+∠A=180°,那么 ∥ 。
3.如图(3),若⊥,⊥,那么a和平行吗?为什么?
答:a______b
理由是: ∵⊥,⊥
∴∠ =∠ =900
∴ ∥ ( ________________,两直线平行)
B 组
4.如图(4),若∠ =∠ ,则AD//BC。
5、如图(5),已知∠3=115 ,∠2=65 ,问直线a、b平行?
解:∵∠3和∠4是对顶角
∴ ∠4=∠3=115 ( 相等)
∵∠2=65
∴∠2+∠4= + =
∴a∥b( ,两直线平行)
6.如图(6),∠1=70 ,∠2=70 ,试说明AB∥CD。
7、如图,直线被直线所截,量得∠1=∠2=∠3。
从∠1=∠2可以得出哪两条直线平行?根据是什么?
从∠1=∠3可以得出哪两条直线平行?根据是什么?
直线互相平行吗?根据是什么?
8.如图,BE是AB的延长线,
由∠CBE=∠A可以判定哪两条直线平行?根据是什么?
由∠CBE=∠C可以判定哪两条直线平行?根据是什么?
第五章 相交线与平行线(七)—平行线的判定(2)
学习目标:1、熟练掌握平行线的概念和判定方法推导过程
2、能灵活运用平行线的判定方法进行解题
学习过程
一、知识点回顾:
1、平行线的定义:________________________________________________
2、平行公理:
①经过直线外一点,__________________条直线与这条直线平行。
②如果两条直线都与第三条直线平行,那么这两条直线也互相________。
几何语言:∵b∥a, c∥a
∴ ________ ∥ ________
3.平行线的判定:
(1) ∵∠1=∠2
∴ ∥ ( _____________,两直线平行)
(2)∵∠3=∠2
∴ ∥ ( ______________,两直线平行)
(3)∵∠4+∠2=180°
∴ ∥ (________________,两直线平行)
(4)∵⊥,⊥,
∴ ∥ ( 的两条直线平行。)
二.练习:
A组:
1.在同一平面内,两条直线的位置关系有 和 两种。
2.下列说法,正确的是( )
(A)不相交的两条直线是平行线; (B)同一平面内,不相交的两要射线平行
(C)同一平面内,两条直线不相交,就是重合;
(D)同一平面内,没有公共点的两条直线是平行线。
3.判断题:
(1)过一点有且只有一条直线与已知直线平行。( )
(2)与同一条直线平行的两直线必平行。( )
(3)与同一条直线相交的两直线必相交。( )
(4)是直线,且⊥,⊥,则⊥。
4.如图4,∠1的内错角是 ;∠2的内错角是 ;
∠BAN的同旁同角是 ;∠CAM的同旁内角是 。
∠B的同旁内角是____________________
5、如图5,直线a、b、c被直线l所截,量得∠1=∠2=∠3
(1)从∠1=∠2可以得出______//______,理由是_________________________
(2)从∠1=∠3可以得出______//______,理由是_________________________
(3)直线a、b、c互相平行吗?________,理由是_________________________
6.如图6,
(1)若∠1=∠B,则可得出 ∥ ,根据是 ;
(2)若∠1=∠5,则可得出 ∥ ,根据是 ;
(3)若∠DEC+∠C=180 ,则可得出 ∥ ,根据是 ;
(4)若∠B=∠3,则可得出 ∥ ,
(5)若∠2=∠C,则可得出 ∥ 。
7.如图,E在AB上,F在DC上,G是BC延长线上的一点:
(1)由∠B=∠1 可以判断直线 ∥ ,
根据是 ;
(2)由∠1=∠D 可以判断直线 ∥ ,
根据是 ;
(3)由∠A+∠D=180 可以判断直线 ∥ ,
根据是 ;
(4)由AD∥BC、EF∥BC可以判断直线 ∥ ,
根据是 ;
B 组:
8.如图,点E在AC的延长线上,下列条件中能判断AB∥CD
的是( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D. ∠D+∠ACD=180
9.如图,∠1=30 ,∠B=60 ,AB⊥AC,
(1)∠DAB+∠B等于多少度?
(2)AD与BC平行吗?AB与CD平行吗?
10.如图,为了加固房屋,要在屋架上加一根横梁DE,合DE∥BC,
如果∠ABC=31 ,∠ADE应为多少度?
11.根据图中所给的条件,找出互相平行的直线和互相垂直的直线。
解:互相平行的线有:
互相垂直的线有:
C 组:
12.观察如图所示的长方体,用符号表示下列两棱的位置关系:
AB, AB,
AD BC
第五章 相交线与平行线(八)—平行线的性质(1)
学习目标:
理解平行线的特征,并会进行简单的应用。
学习过程:
环节一:学习平行线的特征
如右图,直线a、b被直线c所截,且∥,用量角器量出图中八个角的
度数,填在下表中:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
观察右图及上面量得的数据,完成下面的填空:
(1)图中同位角有 ,它们的大小关系是 ;
(2)图中内错角有 ,它们的大小关系是 ;
(3)图中同旁内角有 ,它们的大小关系是 。
3.平行线的特征:
两直线平行, 角相等。
两直线平行, 角相等。
两直线平行, 角 。
环节二:用几何语言表示平行线的性质:
(1)∵a∥b
∴∠1= , ∠2 = ,
∠3= , ∠4 = 。
(两直线平行, 角相等)
(2)∵a∥b
∴∠3= , ∠4 = 。
(两直线平行, 角相等)
(3)∵a∥b
∴∠1+∠2 = ,
∠3+∠4 = 。
(两直线平行, 角 )
环节三:应用
例1 如图,已知直线a∥b,∠1=50°,求∠2的度数。
解: ∵ a∥b,( )
∴∠ =∠1=50°( )
∵∠2和∠3互为邻补角( )
∴________+_______=1800( )
∴∠2=______ =______ =_______
环节四:练习
A组:
1.如图1,已知直线a//b,∠1=650,
则∠2=________,理由是______________________
2.如图2,AB//CD,直线EF分别交CD、AB于E、F两点,
若∠AFE=1080,则∠CEF=_______,理由是_______________
∠DEF=__________,理由是___________________
3.如图3,直线a//b,∠1=540,则
∠2=_______,理由是___________________________;
∠3=________,理由是__________________________;
∠4=________,理由是__________________________;
4、如图4,
(1)∵AD∥BC,
∴∠____=∠1;(两直线平行, )
(2)∵AB∥CD,
∴∠____= ∠1。(两直线平行, )
5、如图5:
(1)∵AD∥BC,
∴∠____+∠ABC =180°;
(两直线平行, )
(2)∵AB∥CD,
∴∠____+∠ABC =180°。(两直线平行, )
B组:
6、如图,AD∥BC,∠B=60°,∠1=∠C。
求∠C的度数。
7、在四边形ABCD中,已知AB∥CD,∠B=60度,求∠C的度数,能否求得∠A的度数?
C组
已知∠B=140度,∠D=125度,求∠BCD的度数;
第五章 相交线与平行线(九)—平行线的性质(2)
一.复习
1.平行线的三条性质可简称为:
性质1:两直线平行, 。
性质2:两直线平行, 。
性质3:两直线平行, 。
2.平行线的性质与判定的关系是:它们的条件和结论恰好 。
二.练习: A组:
1.如图(1),两条直线被第三条直线所截,如果∥,且∠1=70°,
那么∠2= 。
2、如图(2),AB//CD,若∠1=500,则∠2=_________,∠3=__________
3、如图(3),AB//CD,AF交CD于E,∠CEF=600,∠A=_________
4.如图(4),
= 1 \* GB3 ①当 ∥ 时,∠DAC=∠BCA;
②当 ∥ 时,∠ADC+∠DAB=180°;
5.如图(5),若∠A+∠D=180°,则 ∥ ,
所以,∠B+∠C= °
6.如图(6)
①如果DE∥AB,那么∠A+______=180°,或∠B+_____=180°,
根据是 __ ____;
②如果∠CED=∠FDE,那么_______∥______.
根据是_____ ___.
7.如图(6)所示,已知直线AB,CD被直线EF所截,若∠1=∠2,则∠A EF+∠CFE=________.
B 组:
8.如图(7),AB∥CD,BC∥DE,若∠B=60°,则∠D=
9.如(8)图,AD∥BC,∠1=∠2,∠B=70°,则∠C=
10.如图(9),∠1=82°,∠2=98°,∠3=80°,则∠4=
11.如图(10),被所截,∥,得到∠1=∠2的依据是( )
(A)两直线平行,同位角相等; (B)两直线平行,内错角相等;
(C)同位角相等,两直线平行; (D)内错角相等,两直线平行。
12.如图(11)AB∥CD,,那么( )
(A)∠1=∠4 (B)∠1=∠3
(C)∠2=∠3 (D)∠1=∠5
13.如图(12)所示,AB∥CD,则与∠1相等的角(∠1除外)共有( )
A.5个 B.4个 C.3个 D.2个
14、如图,D是AB上一点,E是AC上一点,∠ADE=600,∠B=600,∠AED=400
(1)DE和BC平行吗?为什么?
(2)求∠C的度数
15、如右图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
如图,已知DE∥BC,∠1=25°,∠2=35°,求∠3、∠4的度数
C组:
17、如图,已知∠D=90°,∠1=∠2,EF⊥CD,问:∠B与∠AEF是否相等?若相等,请说明理由。
第五章 相交线与平行线(十)—平行线综合复习卷
一.知识小结:
1、平行线的定义:________________________________________________
2、平行公理:
①经过直线外一点,__________________条直线与这条直线平行。
②如果两条直线都与第三条直线平行,那么这两条直线也互相________。
3.平行线的识别方法:
① ,两直线平行。
② ,两直线平行。
③ ,两直线平行。
④平行于同一条直线的两条直线 。
⑤垂直于同一条直线的两条直线 。
4.平行线的性质:
①两直线平行, 。
②两直线平行, 。
③两直线平行, 。
二.练习:
A组:
1.如图
= 1 \* GB3 ①如果∠1=∠2,那么 ∥
根据 。
②如果∠DAB+∠ABC=180 ,那么 ∥
根据 。
③如果∠3=∠B,那么 ∥
根据 。
2.如图A、B、C、D在同一直线上,AD∥EF,
①若∠E=58°,则∠1= ,
根据: ;
∠2= ,根据: 。
②若∠F=78°,则∠3= ,∠4= 。
3.如图,已知a∥b如果∠1=52 ,那么∠2= ,∠3= ,∠4= 。
4、如图(4)所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路 平行,若第一次拐角是150°,则第二次拐角为________.
B 组:
5.下列说法正确的是( )
(A)不相交的两条直线互相平行;
(B)同位角相等;
(C)同旁内角相等,两直线平行;
(D)在同一平面内,不平行的两条直线相交。
6.∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2的大小关系是( )
(A)∠1=∠2 (B)∠1>∠2
(C)∠1<∠2 (D)无法确定
7.如图,直线相交,∠1=120°,则∠2+∠3=( )
(A)60° (B)90°
(C)120° (D)180°
8.如图,要得到∥,则需要的条件是( )
(A)∠2=∠4 (B)∠1+∠3=180°
(C)∠1+∠2=180° (D)∠2=∠3
9.如图,AB∥EF,∠ECD=∠E,求证:CD∥AB。
证明:∵∠ECD=∠E,
∴EF∥ ,( )
∵AB∥EF,
∴CD∥AB( )
10、如图,a//b,c、d是截线,∠1=800,∠5=700,
求∠2、∠3、∠4的度数
11.如图:直线∥,∠3=85°,求∠1,∠2的度数。
12.如图,AB∥DE,BC∥EF,∠E=72°,求∠B的度数。
13.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,
问:①AC与BD平行吗?为什么?
②AE与BF平行吗?为什么?
C组:
如图,AB//CD,∠B=,∠BEC=,求∠C的度数。
第五章 相交线与平行线(十一)—平行线综合复习卷2
A 组:
一.填空:
1.如图,①当∠C=∠ ,时,AE∥DC,
根据 。
②当 ∥ 时,∠DAB+∠B=180°,
根据 。
2.如图,①若AD∥BC,则∠ =∠ ,
∠ =∠ ( )
②若∠ =∠ ,则AB∥DC,
根据
3.如图,①若∠1=∠2,则可以判定 ∥ ,
根据: 。
②若∠3=∠B,则可以判定 ∥ ,
根据: 。
③若∠4=∠F,则可以判定 ∥ 。
4.如图,已知直线AB∥CD,∠1=70°,那么∠2= °
5.如图,DE∥BC,若∠B=50°,则∠ADE= °;若∠C=75°,则∠DEC= °
二.解答题:
6.如图,已知∠1=∠2,求证:∠3=∠4。
7.如图,AB∥CD,AC与BD相交于E点,且∠B=25°,
求∠D的度数;
不用度量的方法,能否求得出∠C的度数?
B 组:
8.如图,AB⊥EF,CD⊥EF,∠α=∠F=45°,
则与∠FCD相等的角有( )个
(A) 1 (B) 2
(C) 3 (D) 4
9.如图,∥,∠1的度数是∠2的一半,则∠3等于( )
(A)60° (B)100°
(C)120° (D)130°
10.如图,AB∥ED,则∠A+∠C+∠D=( )
(A)180° (B)270°
(C)360° (D)540°
11.如图,AB∥CD,∠B=120°,
∠C=25°,则∠E= °
12.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?请说明理由。
13、已知:AB//CD,BD平分∠ABC,DB平分∠ADC,求证:DA//BC
14.如图,一张长方形纸条ABCD沿MN折叠后形成的图形,∠AMD=40°,求∠BNC 的度数。
SHAPE \* MERGEFORMAT
C组:
15.如图,∠1+∠2=180°,∠DAE=∠BCF,
AE与FC会平行吗?说明理由。
AD与BC的位置关系如何?为什么?
第五章 相交线和平行线( 十二)-------命题和定理
学习目标:了解命题、定理的概念
学习过程:
引例:观察下面几句话,回答问题
(1)我是初一的学生 (4)等式两边加上相同的数,结果仍是等式。
(2)对顶角相等 (5) 画∠AOB=300
(3)请把窗户关上 (6) 两条直线相交有几个交点?
上面几句话中,是对某件事情做出判断的语句有_____________
1、像这样________一件事情的语句,叫做___________,正确的命题成为______命题,错误的命题称为_________命题。
命题常可以写成“如果.........那么.........”的形式。
“如果”后接的部分是__________, “那么” 后接的部分是__________.
3、定理是从公理或其他真命题出发,用逻辑推理的方法判断得到的________
例1:判断下列语句是否是命题,并指出是真命题还是假命题
同角的余角相等 (2)不许大声说话 (3) 连接A、B两点
两点之间,线段最短 (5)等式两边加上相同的数,结果仍是等式。
对顶角不相等
命题是:_________________________________________
真命题是:______________________________________
假命题是:______________________________________
例2:写出下列命题的题设与结论
如果同旁内角互补,那么两直线平行.
题设是_____________________________________
结论是__________________________________________
“若”的题设是____________________,结论是________________
例3.把下列的命题改成“如果.........那么.........”的形式。
两直线平行,同旁内角互补.
___________________________________________________
对顶角相等
_________________________________________________
等角的补角相等.
__________________________________________________-
例4:命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举反例
四.练习
A组
1、判断下列语句是不是命题
(1)延长线段AB( )
(2)两条直线相交,只有一交点( )
(3)画线段AB的中点( )
(4)若|x|=2,则x=2( )
(5)角平分线是一条射线( )
2、分别指出下列各命题的题设和结论。
(1)如果a∥b,b∥c,那么a∥c
___________________________________
(2)内错角相等,两直线平行。
___________________________________
(3)如果,垂足为O,那么
___________________________________
3、分别把下列命题写成“如果……,那么……”的形式。
(1)垂直于同一条直线的两直线平行;
_______________________________________
(2)内错角相等。
________________________________________
B组
判断下列命题是真命题还是假命题,若是假命题,则举一个反例加以说明.
两个锐角的和是锐角;
答:该命题是_______命题 反例:
两条直线被第三条直线所截,内错角相等;
答:该命题是_______命题 反例:
两直线平行,同旁内角互补;
答:该命题是_______命题 反例:
互补的角是邻补角;
答:该命题是_______命题 反例:
2、选择题
(1)下列语句不是命题的是( )
A、两点之间,线段最短 B、不平行的两条直线有一个交点
C、x与y的和等于0吗? D、对顶角不相等。
(2)下列命题中真命题是( )
A、两个锐角之和为钝角 B、两个锐角之和为锐角
C、钝角大于它的补角 D、锐角小于它的余角
(3)命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等。其中假命题有( )
A、1个 B、2个 C、3个 D、4个
3、已知:如图AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF
证明:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2(已知)
∴∠ -∠ =∠ -∠ (等式性质)
∴∠_________=∠_________
∴BE∥CF( )
C组
4.如图,给出下列论断:(1)AB//DC;(2)AD//BC;(3)∠A=∠C,用上面其中两个作为题设,另一个作为结论,用”如果…….那么………”的形式写出一个你认为正确的命题,并加以证明.
第五章平行线和相交线(十三)——平移(1)
学习目标
通过具体实例认识平移变换,理解平移的基本内涵,理解平移前后两图形之间的关系,会找图形的对应点,对应角,对应线段,会画出平移后的图形。
学习过程
一、知识回顾
如图,看图填空
(1) ()
(2)
二、新课
1、观察下面的图案,它们有什么共同的特点?你能否想象出图案是如何绘制的
2、从以下生活中实例中你可以得出什么结论?
(1)传送带上的电视机移动方向从点移动到点、作___ 运动;
(2)传送带上的电视机的在运动前后大小形状没有发生改变,只是_ 改变了;
(3)如果电视机的屏幕沿AA’方向移动了4 m;那么电视机的其他部位(如电视的左上角)也沿方向移动移动了______ m;
3、我们使用直尺与三角尺画平行线时,我们把点A与点A′叫做对应点,把线段AB与线段A′B′叫做对应线段,∠A与∠A′叫做对应角.
此时:点B的对应点是点 ;点C的对应点是点 ;
线段AC的对应线段是线段 ;
线段BC的对应线段是线段 ;
∠B的对应角是 ;∠C的对应角是 .
△ABC平移的方向就是由点B到点B′的方向,
平移的距离就是线段 的长度.
平移的概念:我们把一个图形整体沿某一________移动一定______,会得到一个新的图形,.图形的这种运动叫做平移变换,简称平移.新图形的每一点,都是由原图形的某一点移动后得到的,这两个点称为对应点.
小结:
1、平移是由 和 所决定;
2、图形平移前后___ __和__ ___不变,只是__ ___变了;
3、平移前后两个图形对应线段 ,对应角 ;
例1、如图,把△ABC沿着射线NM方向平移到△A′B′C′,
则:点A的对应点是点 ;
线段AC的对应线段是线段 ,
∠C的对应角是 ,
平移的方向除了用射线NM方向表述外,
还可以表述为__________________
量出平移的距离为:
练习: A组
1、下面各图案中属于平移关系的是( )
A.(1)和(2) B.(1)和(3)
C.(1)和(4) D.(3)和(4)
2、下列运动中,属于物体平移的是 (填编号)
(1)大风车的转动; (2)电梯的升降; (3)火车在笔直的铁轨上行驶;
(4)飞机起飞前在跑道上加速滑行; (5)滑雪运动员在雪地上滑翔
3.下列现象是数学中的平移的是( )
A.冰化成水 B.电梯由一楼升到二楼
C.导弹击中目标后爆炸 D.卫星绕地球运动
4.在下面的六幅图中,(2)(3)(4)(5)(6)中的图案_________可以通过平移图案(1)得到的.
5、如图2的图案中,可以看出由图案自身的部分经过平移而得到的是( )
6.如图,△ABC平移后得到△DEF,已知∠B=35°,∠A=85°, AB=2cm,AC=1cm,
则,DE= cm。∠D= °∠F=______°
7.如图,△ABC平移到△A′B′C′的位置.
(1)方向是________________ ,
量出平移的距离是________.
(2)点D、E、F经过平移到了什么位置?
请将他们的对应点D′、E′、F′在
图上标出。
B组
1、 如图1,图形(1)沿射线XY平移后得到图形(2) 请在图形中标出点A和点B′的对应点、线段OC的对应线段。
2、如图2,小船经过平移到了新的位置,你发现缺少什么?请补上。
3、如图3,把图中多边形ABCD沿着箭头平移
6格,得到一个多边形,请画出此多边形,
并完成以下问题。
回答:
点A、D的对应点分别是:点 ;
线段BC、CA的对应线段分别是:线段 、 ;
∠A、∠C的对应角分别是:
4、如图4,将△ABC沿着箭头GH方向移动3cm得△DEF,画出△DEF
第五章平行线和相交线(十四)------平移(2)
学习目标:能按要求作出简单平面图形平移后的图形,掌握平移的特征,并会应用。
试一试:
如图, △ABC沿着PQ的方向平移到△A′B′C′的位置,连结对应点A A′,B B′,C C′,
对于它们的大小关系和位置关系,你有什么发现 写出你的结论.
归纳:
平移的特征:(1)图形的形状与大小 ;
(2)对应线段 ;
(3)对应角 ;
(4)对应点所连的线段 ;
例:如图,平移△ABC,使点A移动到点A′,
画出平移后的△A′B′C′.
练习
A组
一、选择题
1、下列A、B、C、D四幅图案中,能通过平移图案(1)得到的是( )
(1) A. B. C. D.
2、如图所示的图形中用其中一部分平移可以得到的是( )
3. 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
A. 先向下移动1格,再向左移动1格;
B. 先向下移动1格,再向左移动2格
C. 先向下移动2格,再向左移动1格;
D. 先向下移动2格,再向左移动2
4、如图所示的正方体的棱长为2cm,将线段AC
平移到A1C1的位置上,平移的距离是( )
A.1cm B.2cm
C.4cm D.无法求出
5、.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长; B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长; D.沿射线BD的方向移动DC长
二、解答题
1.如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对 应点D、点C的对应点F的位置.
2.如图,将方格纸中的小船先向左平移4倍,再向下平移5格,画出平移后的图形.
B组
一、填空
1.如图所示,平移△ABC可得到△DEF,如果∠A=50°,
∠C=60°,那么,∠EDF=_______度, ∠F=______度,
2.如图5长方形ABCD中,对角线AC与BD相交于O,DE∥AC,CE∥BD,那么△DCE可以看作是△________平移得到的,平移的距离是线
段________的长.
3.如图,在矩形ABCD中,AD=2AB,E、F分别为AD、BC的中点,扇形BFE、FCD的半径FB、CF的长度均为1cm,求阴影部分的面积为_______
二、解答题
1.如图,∠DEF是由∠ABC经过平移后得到的,DE交BC于G,若∠DGC=30°,求∠B的度数及∠E的度数.
三、利用如图所示的图形,通过平移设计美丽的图案
( http: / / )
C 组
1、如图、一个正方形毛巾的边长为30cm,上面横竖各有两道毛巾红条(红条外的其他部分为白色),宽度都是5cm,试求出此正放行毛巾的白色部分面积。
(反思:你想到了几种求解的方法?能利用平移的知识求解吗?)
第五章平行线和相交线(十五)——复习(1)
知识点回顾
一、邻补角与对顶角
邻补角的性质:邻补角__________; 对顶角的性质:对顶角_________
练习1、如图所示,∠1和∠2是对顶角的图形有( )毛
A B C D
2、如图所示,直线AB,CD,EF相交于点O,
(1) ∠AOD的对顶角是________,
∠EOC的对顶角是_________
(2)∠AOC的邻补角是_________________;∠EOB的邻补角是________________;
二、垂线的定义和性质
1、定义:几何语言:(正用)
(反用)
练习(1)、如图:,垂足为O,EF经过点O,
若 则
2、垂线的性质一:经过一点有且__________条直线和已知直线垂直.
练习(2)分别过点P作线段AB的垂线MN
3、点到直线的距离.
如图垂足为O,则线段_______的长度
叫作点到直线l的距离
垂线的性质二:垂线段_________.
练习
(1)(如图)AC⊥BC,CD⊥AB,AC=4,CB=3,AB=5,
C点到AB的距离是线段______的长度,
B点到AC的距离是________,
A点到BC的距离________,.
(2)计划把河水引到水池A中,可以先引______⊥CD,垂足为_____,
然后沿AB开渠,则能使所开的渠最短,
这样设计的依据是________________
三、相交线中的同位角,内错角,同旁内角
练习1、如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
(A)①、②、③ (B)①、②、④
(C)②、③、④ (D) ①、②、③、④
四、平行线的判定和性质
1、在同一平面内,与已知直线平行的直线有 条。
2、而经过直线外一点,与已知直线平行的直线有且只有 条。
3、平行于同一条直线的两条直线 。
练习1:如图:
(1)如果∠1=∠B,那么根据 ,可得AD∥BC。
(2)如果∠D=∠1,那么根据 ,可得AB∥CD。
(3)如果∠BAD+∠ABC=180 ,那么根据同旁内角互补,
两直线平行,可得 ∥ 。
(4)如果∠BCD+∠ABC=180 ,那么根据同旁内角互补,
两直线平行,可得 ∥
练习2:已知∠1=∠B,求证:∠2=∠C
证明:∵∠1=∠B(已知)
∴DE∥BC( )
∴∠2=∠C( )
五、命题
(1)下列句子中,__________是命题
①相等的角是对顶角 ②这两条直线平行吗 ③过A作直线的垂线 ④5x-x=2x
(2)把命题“同一平面内两条不平行的直线必相交”写成“如果……,那么……”的形式____________________________________________.
(3)”相等的角是对顶角”是____命题.(填”真””假”),并指出命题的
题设是_________________.结论是_____________________
六、平移
练习.如图,平移四边形ABCD到四边形EFGH,使得点C移到点G的位置,则有:
(1)对应线段AB= ,DA= ;对应线段BC∥ ,CD∥ ;
(2)对应角∠B= ,∠D= ;
(3)将图中所有对应点用虚线连结起来,得到的线段有 , , , ;
它们的关系是 。
练习A组:
1、过P作出OB、OA的垂线
2、AB∥DF,DE∥BC,∠1=65°求∠2、∠3的度数
3、已知,求的度数
C组
1、已知:如图 2-85,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,
求∠BOF度数.
第五章平行线和相交线(十六)——复习(2)
A 组
(一)、填空题
1. 如图1,直线AB和CD相交于点O,OE是∠DOB的平分线,若∠AOC=76°,则∠EOB=_______.
2.如图2,已知直线AB,CD相交于O,OE⊥AB,∠1=25°,
则∠2=_____度,∠3=_____度,∠4=______度.
3.如图3,OA⊥OB,OC⊥OD.若∠AOD=144°,则∠BOC=______.
4.如图4,AB∥CD、AF分别交AB、CD于A、C.CE平分∠DCF,
∠1=100,则∠2= .
5.如图,AB∥CD.若∠2是∠1的两倍,则∠2等于_______
(二)、选择题
1、下列命题中,是真命题的是( )
(A)相等的两个角是对顶角. (B)有公共顶点的两个角是对顶角.
(C)一条直线只有一条垂线. (D)过直线外一点有且只有一条直线垂直于已知直线.
2.如图,下列推理正确的是( )
(A)∵∠1=∠2,∴ AD∥BC (B)∵∠3=∠4,∴ AB∥CD
(C)∵∠3=∠5,∴ AB∥DC (D)∵∠3=∠5,∴ AD∥BC
3、如图,AB∥CD,AD∥BC,则下列各式中正确的是( )
A.∠1+∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3大小无关
(三)完成下列推理
1、如图,已知∠1=1350,∠8=450,直线a与b平行吗 说明理由:
(1)∵∠1=1350 (已知)
∴ ∠2=180°-∠____=_____
∴∠2=∠
∴ a∥b( )
(2)∵∠8=450(已知)
∴ ∠6=∠8=450 ( )
∴ + =1800
∴ a∥b ( );
2、如图,∠B=∠D,∠1=∠2.求证:AB∥CD.
【证明】∵ ∠1=∠2(已知),
∴ ∥ ( ),
∴ ∠DAB+∠ =180°( ).
∵ ∠B=∠D(已知),
∴ ∠DAB+∠ =180°( ),
∴ AB∥CD( ).
(四)证明
1、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE
2、已知:如图,AD∥EF,∠1=∠2.求证:AB∥DG.
B组
五、证明
1、已知:如图2-82,DE∥BC,∠ADE=∠EFC,
求证:∠1=∠2
2、如图,已知AB∥CD,试再添上一个条件,使∠1=∠2成立(要求给出两个以上答案)
3、作∠AOB=90°,在OA上取一点C,使OC=3cm,在OB上取一点D,使OD=4cm,用三角尺过C点作OA的垂线,经过D点作OB的垂线,两条垂线相交于E
⑴量出∠CED的大小
⑵量出点E到OA的距离,点E到OB的距离
C组
1、画出一个边长为2cm的正方形,然后画出该正方形向北偏东30°方向平移4cm后的图形。
1
A
C
B
D
O
2
3
4
a
b
1
2
3
4
图1
A B C D
图2
图3
图4
图5
图6
图7
图8
图8
5
3
4
图2
图1
B
B
P
A
A
B
D
C
图1
图2
图1
图4
图3
图5
图6
图8
图7
图9
图(一)
图(二)
图(5)
图(6)
图4
图5
图6
图1
图2
图3
图4
图5
(3)
(2)
D
A
B
C
E
A
B
M
D
C
N
C
A
B
D
E
F
1
2
图2
图3
图4
A
B
C
D
O
A
D
E
B
C
1
2
A
D
F
B
E
C
1
2
3
D
E
A
B
C
2
1
C
D
F
E
B
A
1
2
- 1 -
第五章相交线与平行线(一)— 相交线
学习目标:
1、经历观察、推理、交流等过程,了解邻补角和对顶角的概念,
2、掌握邻补角、对顶角的性质;
学习过程
环节一:复习引入
1、复习提问:若∠1和∠2互余,则________________
若∠1和∠2互补,则________________
2、画图:作直线AB、CD相交于点O
3、探究新知
两直线相交 所形成的角 分类 位置关系 大小关系
∠1和∠2 ,∠2和∠___∠__和∠__,∠__和∠__
∠1和∠3, ∠__和∠__
归纳:
有一条公共边,而且另一边互为反向延长线的两个角叫做互为________。如图中的______和_______
如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫做互为_________。如图中的_________和__________
3、想一想:如果改变∠1的大小, ∠1和∠2还是邻补角吗?_______,它们的大小关系是____________。∠1和∠3还是对顶角吗?_______,它们的大小关系是________
结论:从数量上看,邻补角__________,对顶角都_______________
环节二:例题
例:如图,直线a,b相交,∠1=400,求∠2,∠3,∠4的度数
解:∵直线a,b相交
∴∠1+∠2=1800(邻补角的定义)
∴ ∠2=__________________
=__________________
=__________
∵直线a,b相交
∴∠3=∠____=________
∠4=∠____=_________( )
环节三:练习
A组
1、如图所示,∠1和∠2是对顶角的图形是( )毛
2、如图1,AB与CD相交所成的四个角中,∠1的邻补角是______,
∠1的对顶角___.
3、如图2所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:________________;
(2)写出∠COE的邻补角:_________________.
(3)写出与∠BOC的邻补角:_______________.
4、如图3所示,若∠1=25°,则∠2=_______,理由是____________
∠3=______,理由是__________________
∠4=_______.,理由是_______________
5、如图4所示,已知直线AB,CD相交于O,OA平分∠EOC,
∠EOC=70°,则∠AOC=_________,∠BOD=______.
6、如图5所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,
则∠AOD=________∠AOC= ______________
B组
7、下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
8、如图6所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,
∠AOC的邻补角是_________;
若∠AOC=50°,则∠BOD=______,∠COB=_______.
9、如图6所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
10、如图7,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
11、如图8,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,
求∠BOD,∠AOE的 度数.
C组
13、如图8所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,则∠EOD=________.
第五章相交线与平行线(二)—垂线
学习目标:
1、明确垂线的定义,并能过已知点画已知直线的垂线;明确垂线的性质;
2、能用简单的数学语言叙述图形的某些位置关系;
探究一:
1、画图:作直线AB、CD相交于点O。
2、画图:作直线AB、CD相交于点O,使∠AOD=90°,
回答:此时∠BOD= °,∠AOC= °,∠BOC= °
3、定义:
两直线AB、CD相交于点O,当所构成的四个角中有一个为 时,直线AB、CD互相垂直,交点O叫做 ,记作 ⊥ ,垂足为O。
探究二:垂线的画法:(可用三角板或量角器作图)
1、填表
如图,经过直线AB外一点P,画直线CD与已知直线AB垂直。 如图,经过直线AB上一点P,画直线CD与已知直线AB垂直。
2、小组讨论:
①组内是否有不同的画法?
②过点P作AB的垂线,这样的垂线有 条。
3、结论:
在同一平面内,经过直线外或直线上一点, 条直线与已知直线垂直。
探究三:
1.画图:已知直线l与直线外一点A
①过A作AO⊥l,垂足为O;
(我们称AO为点A到直线 的垂线段)
②在直线l上任取两点B、C;
③连结AB、AC;
2.用刻度尺度量得:AB= , AC= ,AO=
3.比较线段AC、线段AB、线段AO中最短的线段是:线段
4.小组交流:
看看同小组其他同学第3题的结果,你发现了什么?
5.阅读课本第5-6页回答:
(1)直线外的一点到这条直线的垂线段的________ ,叫做点到直线的距离
(2)连直线外一点与直线上各点连结而得的所有线段中,与直线 的那条线段最短;
简称为: 最短;
练习 A组
1、比一比,谁能更快地完成下列练习。
(1)过直线CD上一点P作直线CD的垂线。
(2)过直线CD上一点P作直线AB的垂线
2、如图1,AC⊥BC,AC=3,BC=4,AB=5,则B到AC的距离是_______,点A到BC的距离
是________,A、B之间的距离是__________
3、如图2,画AE⊥BC,CF⊥AD,垂足分别为E、F
4、如图:已知直线AB以及直线AB外一点P,按下述要求画图并填空:
过点P画PC⊥AB,垂足为点C;
P、C两点的距离是线段 的长度;
点P 到直线AB的距离是线段 的长度;
点P到直线AB的距离为 (精确到1mm)
5、画一条线段或射线的垂线,就是画它们所在直线的垂线,如图,请你过点P画出线段AB或射线AB的垂线
(1) (2) (3)
·P ·P
B 组
6、分别画出下列三个三角形中AB边上的高CD,并量出顶点C到AB的距离。
7、如图,在铁路(直线)旁有一村庄A,现在要建火车站,为方便该村庄的人乘车,
火车站应建在什么位置?请画图表示出来。
解:过点A作
火车站应建在 点处。
由是
第五章相交线与平行线(三)—相交线中的角
学习目标
1、明确什么是同位角、内错角、同旁内角
2、能正确找出图中的同位角、内错角、同旁内角
复习回顾:
两条直线相交,可得几个角,这些角有什么关系?
图 形 相等的角有 互补的角有
探索:
1、如图,已知直线AB、直线CD,画直线EF分别与AB、CD相交于点M、N,
问:图中共有_______个角,分别是__________________________________
A
2、填表:(观察以下的角与直线a、b、l位置关系,并填写下表)
表一:
∠2和∠6 位于直线a、b的___方,位于直线l的___侧
∠3和∠7 位于直线a、b的___方,位于直线l的___侧
∠1和∠5 位于直线a、b的___方,位于直线l的___侧
∠4和∠8 位于直线a、b的___方,位于直线l的___侧
像以上每一对角,都在直线l的同侧,直线a、b的上方,这样位置的一对角是 角。
表二:
∠3和∠5 位于直线a、b的_____,位于直线l的______
∠4和∠6 位于直线a、b的_____,位于直线l的______
像以上每一对角,都在直线l的_______,直线a、b_______,这样位置的角是________ 角;
表三:
∠3和∠6 位于直线a、b的______,位于直线l的______
∠4和∠5 位于直线a、b的______,位于直线l的______
像以上每一对角,都在直线l的_______,直线a、b_______,这样位置的角是 角;
练习 A组
1、如图,图中同位角有_____对,分别是
内错角有______对,分别是
同旁内角有_____对,分别是_________________
2、如图,与∠1是同位角的是_______________;
与∠2是内错角的是 ;
与∠1是同旁内角的是 __________________;
与∠2互为补角的是 ;
∠2的对顶角是 。
3、如图,∠1与∠D是________角;
∠1与∠B是________角;∠B和∠C
是________角,∠D和∠C是________角。
4、如图,与∠DAB是内错角是: ;
与∠EAC是内错角是: ;
与∠B是同旁内角的是: ____ ___.
B组
5、找出图中的内错角: ;
找出图中的同位角: ;
6、如图,找出图中∠1的内错角: _____
∠2的内错角:
7、如图,∠1和∠2是两条直线_________和__________被直线_________所截而成的_________角,∠3和∠4是两条直线________和________被直线________所截而成的_________角。
8、在图中画出一条直线,使图中出现∠AOD的同位角,
说明哪一个角是∠AOD的同位角,并画出图形;
解:图中,∠ 与∠AOD是同位角;
C 组
9、∠1是直线a、b相交所成的角,用量角器量出∠1的度数,画一条直线c,使得直线c与直线b相交所成的角中有一个与∠1相等.
第五章 相交线(四)----练习
知识点回顾:
1、对顶角、邻补角
如图,直线AB与直线CD交于点O,则∠1的
对顶角是_______,∠1的邻补角是_________
从数量上看,邻补角__________,对顶角______________
2、垂线
(1)如图1,∵AB⊥CD,垂足为O
∴__________________________
(2)如图1,∵∠BOC=900
∴____________________________
(3)在同一平面内,经过直线外或直线上一点,
条直线与已知直线垂直。
(4)连接直线外一点与直线上各点的所有线段中, 最短;
直线外的一点到这条直线的垂线段的________ ,叫做点到直线的距离
画图:过点P作直线CD⊥直线AB,垂足为O
·P
A B
则__________________叫做点P到直线AB的距离。
3、三线八角
如图,直线a、b被直线l所截,构成八个角,则
(1)∠1和∠5是___________,
类似的还有___________________________
(2)∠3和∠5是___________,
类似的还有___________________________
(3)∠4和∠5是___________,
类似的还有___________________________
练习: A组
1、如图1,直线AB、CD、EF相交于点O
(1)∠AOC的邻补角是________________
∠BOE的邻补角是__________________
(2)∠DOA的对顶角是_____________
∠EOC的对顶角是_____________
(3)如果∠AOC=500,
则∠BOD=_________,理由是______________________
∠COB=_________,理由是______________________
2、如图2,∠EOC的邻补角是_______,∠BOC的邻补角是_____________
3、如图3,若∠1=300,∠2=400,则∠3=________,∠4=_________,∠5=________
4、如图4,直线AB、CD相交于点O,且∠AOC+∠BOD=1200,则∠BOC=________
5、如图5,点O是直线AB上一点
(1)若OC⊥OD,∠AOC=350,则∠BOD=____________ ;
(2)若∠AOC=400,∠BOD=500,则∠COD=___________,OC________OD
6、如图6,若OC⊥AB,∠1=300,则∠2=____________
B 组
7、如7图,∠ABC的同位角是 :
∠ABC的内错角是 :
∠ABC的同旁内角是
8、如图8,∠AFD的同位角是 :
∠AFG的内错角是 :
∠BGF的同旁内角是
9、如图9, ∠AME的同位角是___ ____:
∠MNP的内错角是 _:
∠MOP的同旁内角是 _____
10、画过A作BC的垂线
11、如图,△ABC中,∠C=900,△ABC的三条边AB、BC、CA中,
最长的是_________,理由是___________________________
12、如右图:,图中共有______个直角, 线段________的长表示点C到AB的距离,线段________的长表示点A到BC的距离.
13、如图. 直线CD过点O,且,求的度数.
C组
14、如图,(1)用量角器画∠AOB的平分线OC,
(2)在OC上任取一点P,画出点P到OA的距离PM
(3)画出点P到OB的距离PN
(4)比较PM、PN的大小
第五章 相交线与平行线(五)—平行线及其公理
学习目标
1、感受平行线的概念,能作出已知直线的平行线。
2、了解平行线的公理及其推论。
学习过程
环节一:学习平行线的定义
1.填表:
用目测画二条直线,使它们互相平行 画二条不平行的直线
EMBED Equation.DSMT4
2、阅读课本第12页,回答:
平行线的定义:
3、我们如何用几何语言描述平行线?
直线AB与CD平行,记作 AB∥CD
直线m与n平行,记作
环节二:学行线有关的公理
1.填空:
①点A在直线外,经过点A作一直线
小组讨论:直线和的位置关系
和的第一种位置关系:
和的第二种位置关系:
思考:经过直线外一点有 条直线与已知直线平行?
②分别画二条与直线平行的直线和
观察你上面所画的图形,可知直线和之间的位置关系是:
2、与平行线有关的公理(要求记忆)
①平行公理:经过直线外一点,有且只有 条直线与这条直线平行.
②如果两条直线都与第三条直线平行,那么这两条直线也互相 。
几何语言:
∵b∥a, c∥a
∴ ∥
环节三:练习
A组:
1.两条直线相交,交点的个数是 个;两条直线平行,交点的个数是 个。
2.判断题:
(1)不相交的两条直线叫做平行线。( )
(2)如果一条直线与两条平行线中的一条直线平行,那么它与另一条直线也互相平行。( )
(3)过一点有且只有一条直线平行于已知直线。( )
3.一条直线与另两条平行直线的关系是( )
A.一定与两条平行线平行; B.可能与两条平行线的一条平行,一条相交;
C.一定与两条平行线相交; D.与两条平行线都平行或都相交。
4.在同一平面内的两条直线的位置关系可能有( )
A.两种:平行与相交 B.两种:平行与垂直
C.三种:平行、垂直与相交 D.两种:垂直与相交
5.下列表示方法正确的是( )
A.∥A B.AB∥A C.∥ D.∥
B 组:
6.同一平面内的三条直线,其交点的个数可能为 。
7.下列说法中,错误的是( )
A.如果⊥,⊥,那么∥; B.如果∥,∥,那么∥;
C.⊥,∥,那么⊥; D.有且只有一条直线与已知直线平行。
8.读下列语句并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
(2)直线AB,CD是相交线,点P是直线AB,CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E。
9、如图,直线a、b被直线l所截
(1)∠5的同位角是_______,∠5的内错角是_______,∠5的同旁内角是________
(2)如果∠5=∠3,那么∠5与∠1有何关系?为什么?
(3)如果∠5+∠4=1800,那么∠5与∠1有何关系?
为什么?
C 组:
如图,梯形ABCD中AB∥CD,连接DB,过C画DB的平行线与AB的延长线交于F,并度量DC与BF的长度,比较DB与CF的大小。
第五章相交线与平行线(六)—平行线的判定(1)
学习目标
1、感受平行线判定方法的推导过程,了解并掌握三种判定方法。
2、能灵活运用平行线的判定方法进行解题。
学习过程
环节一:学习用三角板推平行线
1、先看教师示范用一块三角板借助黑板的一边作出一组平行线。
2、每人尝试借助两块三角板作一条直线与已知直线平行。然后画一条直线与a、b相交;
环节二:学习平行线的识别。
1、(1)观察图(一)∠1和∠2________角,由作图过程可知∠1和∠2的大小关系是__________,此时直线a和b_______________
(2)思考:在图(二)中标出一对同位角∠3和∠4,
那么它们的大小关系是______
(3)结论:同位角 ,两直线平行。
几何表示:如图
∵∠1=∠2
∴a//b(__________________,两直线平行)
2、如图,∠2和∠3是______角,当∠2=∠3时,直线a和b的位置关系是:______
理由:
3、如图,∠2和∠4是______角,当它们满足:__________时,a//b
理由:
4、结论:内错角 ,两直线平行。
同旁内角 ,两直线平行。
5、几何语言表示平行线的识别方法:(要求记忆)
(1) 同位角相等,两直线平行
∵∠1=∠2
∴ ∥ (同位角______,两直线平行)
(2)内错角相等,两直线平行
∵∠3=∠2
∴ ∥ ( 内错角______,两直线平行)
(3)同旁内角互补,两直线平行
∵∠4+∠2=180°
∴ ∥ ( 同旁内角_______,两直线平行)
环节三:练习 A组
1.如图(1),
若∠1=∠2,则
2.如图(2)
如果∠1=∠A,那么 ∥ ;
如果∠1=∠F,那么 ∥ ;
如果∠FDA+∠A=180°,那么 ∥ 。
3.如图(3),若⊥,⊥,那么a和平行吗?为什么?
答:a______b
理由是: ∵⊥,⊥
∴∠ =∠ =900
∴ ∥ ( ________________,两直线平行)
B 组
4.如图(4),若∠ =∠ ,则AD//BC。
5、如图(5),已知∠3=115 ,∠2=65 ,问直线a、b平行?
解:∵∠3和∠4是对顶角
∴ ∠4=∠3=115 ( 相等)
∵∠2=65
∴∠2+∠4= + =
∴a∥b( ,两直线平行)
6.如图(6),∠1=70 ,∠2=70 ,试说明AB∥CD。
7、如图,直线被直线所截,量得∠1=∠2=∠3。
从∠1=∠2可以得出哪两条直线平行?根据是什么?
从∠1=∠3可以得出哪两条直线平行?根据是什么?
直线互相平行吗?根据是什么?
8.如图,BE是AB的延长线,
由∠CBE=∠A可以判定哪两条直线平行?根据是什么?
由∠CBE=∠C可以判定哪两条直线平行?根据是什么?
第五章 相交线与平行线(七)—平行线的判定(2)
学习目标:1、熟练掌握平行线的概念和判定方法推导过程
2、能灵活运用平行线的判定方法进行解题
学习过程
一、知识点回顾:
1、平行线的定义:________________________________________________
2、平行公理:
①经过直线外一点,__________________条直线与这条直线平行。
②如果两条直线都与第三条直线平行,那么这两条直线也互相________。
几何语言:∵b∥a, c∥a
∴ ________ ∥ ________
3.平行线的判定:
(1) ∵∠1=∠2
∴ ∥ ( _____________,两直线平行)
(2)∵∠3=∠2
∴ ∥ ( ______________,两直线平行)
(3)∵∠4+∠2=180°
∴ ∥ (________________,两直线平行)
(4)∵⊥,⊥,
∴ ∥ ( 的两条直线平行。)
二.练习:
A组:
1.在同一平面内,两条直线的位置关系有 和 两种。
2.下列说法,正确的是( )
(A)不相交的两条直线是平行线; (B)同一平面内,不相交的两要射线平行
(C)同一平面内,两条直线不相交,就是重合;
(D)同一平面内,没有公共点的两条直线是平行线。
3.判断题:
(1)过一点有且只有一条直线与已知直线平行。( )
(2)与同一条直线平行的两直线必平行。( )
(3)与同一条直线相交的两直线必相交。( )
(4)是直线,且⊥,⊥,则⊥。
4.如图4,∠1的内错角是 ;∠2的内错角是 ;
∠BAN的同旁同角是 ;∠CAM的同旁内角是 。
∠B的同旁内角是____________________
5、如图5,直线a、b、c被直线l所截,量得∠1=∠2=∠3
(1)从∠1=∠2可以得出______//______,理由是_________________________
(2)从∠1=∠3可以得出______//______,理由是_________________________
(3)直线a、b、c互相平行吗?________,理由是_________________________
6.如图6,
(1)若∠1=∠B,则可得出 ∥ ,根据是 ;
(2)若∠1=∠5,则可得出 ∥ ,根据是 ;
(3)若∠DEC+∠C=180 ,则可得出 ∥ ,根据是 ;
(4)若∠B=∠3,则可得出 ∥ ,
(5)若∠2=∠C,则可得出 ∥ 。
7.如图,E在AB上,F在DC上,G是BC延长线上的一点:
(1)由∠B=∠1 可以判断直线 ∥ ,
根据是 ;
(2)由∠1=∠D 可以判断直线 ∥ ,
根据是 ;
(3)由∠A+∠D=180 可以判断直线 ∥ ,
根据是 ;
(4)由AD∥BC、EF∥BC可以判断直线 ∥ ,
根据是 ;
B 组:
8.如图,点E在AC的延长线上,下列条件中能判断AB∥CD
的是( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D. ∠D+∠ACD=180
9.如图,∠1=30 ,∠B=60 ,AB⊥AC,
(1)∠DAB+∠B等于多少度?
(2)AD与BC平行吗?AB与CD平行吗?
10.如图,为了加固房屋,要在屋架上加一根横梁DE,合DE∥BC,
如果∠ABC=31 ,∠ADE应为多少度?
11.根据图中所给的条件,找出互相平行的直线和互相垂直的直线。
解:互相平行的线有:
互相垂直的线有:
C 组:
12.观察如图所示的长方体,用符号表示下列两棱的位置关系:
AB, AB,
AD BC
第五章 相交线与平行线(八)—平行线的性质(1)
学习目标:
理解平行线的特征,并会进行简单的应用。
学习过程:
环节一:学习平行线的特征
如右图,直线a、b被直线c所截,且∥,用量角器量出图中八个角的
度数,填在下表中:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
观察右图及上面量得的数据,完成下面的填空:
(1)图中同位角有 ,它们的大小关系是 ;
(2)图中内错角有 ,它们的大小关系是 ;
(3)图中同旁内角有 ,它们的大小关系是 。
3.平行线的特征:
两直线平行, 角相等。
两直线平行, 角相等。
两直线平行, 角 。
环节二:用几何语言表示平行线的性质:
(1)∵a∥b
∴∠1= , ∠2 = ,
∠3= , ∠4 = 。
(两直线平行, 角相等)
(2)∵a∥b
∴∠3= , ∠4 = 。
(两直线平行, 角相等)
(3)∵a∥b
∴∠1+∠2 = ,
∠3+∠4 = 。
(两直线平行, 角 )
环节三:应用
例1 如图,已知直线a∥b,∠1=50°,求∠2的度数。
解: ∵ a∥b,( )
∴∠ =∠1=50°( )
∵∠2和∠3互为邻补角( )
∴________+_______=1800( )
∴∠2=______ =______ =_______
环节四:练习
A组:
1.如图1,已知直线a//b,∠1=650,
则∠2=________,理由是______________________
2.如图2,AB//CD,直线EF分别交CD、AB于E、F两点,
若∠AFE=1080,则∠CEF=_______,理由是_______________
∠DEF=__________,理由是___________________
3.如图3,直线a//b,∠1=540,则
∠2=_______,理由是___________________________;
∠3=________,理由是__________________________;
∠4=________,理由是__________________________;
4、如图4,
(1)∵AD∥BC,
∴∠____=∠1;(两直线平行, )
(2)∵AB∥CD,
∴∠____= ∠1。(两直线平行, )
5、如图5:
(1)∵AD∥BC,
∴∠____+∠ABC =180°;
(两直线平行, )
(2)∵AB∥CD,
∴∠____+∠ABC =180°。(两直线平行, )
B组:
6、如图,AD∥BC,∠B=60°,∠1=∠C。
求∠C的度数。
7、在四边形ABCD中,已知AB∥CD,∠B=60度,求∠C的度数,能否求得∠A的度数?
C组
已知∠B=140度,∠D=125度,求∠BCD的度数;
第五章 相交线与平行线(九)—平行线的性质(2)
一.复习
1.平行线的三条性质可简称为:
性质1:两直线平行, 。
性质2:两直线平行, 。
性质3:两直线平行, 。
2.平行线的性质与判定的关系是:它们的条件和结论恰好 。
二.练习: A组:
1.如图(1),两条直线被第三条直线所截,如果∥,且∠1=70°,
那么∠2= 。
2、如图(2),AB//CD,若∠1=500,则∠2=_________,∠3=__________
3、如图(3),AB//CD,AF交CD于E,∠CEF=600,∠A=_________
4.如图(4),
= 1 \* GB3 ①当 ∥ 时,∠DAC=∠BCA;
②当 ∥ 时,∠ADC+∠DAB=180°;
5.如图(5),若∠A+∠D=180°,则 ∥ ,
所以,∠B+∠C= °
6.如图(6)
①如果DE∥AB,那么∠A+______=180°,或∠B+_____=180°,
根据是 __ ____;
②如果∠CED=∠FDE,那么_______∥______.
根据是_____ ___.
7.如图(6)所示,已知直线AB,CD被直线EF所截,若∠1=∠2,则∠A EF+∠CFE=________.
B 组:
8.如图(7),AB∥CD,BC∥DE,若∠B=60°,则∠D=
9.如(8)图,AD∥BC,∠1=∠2,∠B=70°,则∠C=
10.如图(9),∠1=82°,∠2=98°,∠3=80°,则∠4=
11.如图(10),被所截,∥,得到∠1=∠2的依据是( )
(A)两直线平行,同位角相等; (B)两直线平行,内错角相等;
(C)同位角相等,两直线平行; (D)内错角相等,两直线平行。
12.如图(11)AB∥CD,,那么( )
(A)∠1=∠4 (B)∠1=∠3
(C)∠2=∠3 (D)∠1=∠5
13.如图(12)所示,AB∥CD,则与∠1相等的角(∠1除外)共有( )
A.5个 B.4个 C.3个 D.2个
14、如图,D是AB上一点,E是AC上一点,∠ADE=600,∠B=600,∠AED=400
(1)DE和BC平行吗?为什么?
(2)求∠C的度数
15、如右图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
如图,已知DE∥BC,∠1=25°,∠2=35°,求∠3、∠4的度数
C组:
17、如图,已知∠D=90°,∠1=∠2,EF⊥CD,问:∠B与∠AEF是否相等?若相等,请说明理由。
第五章 相交线与平行线(十)—平行线综合复习卷
一.知识小结:
1、平行线的定义:________________________________________________
2、平行公理:
①经过直线外一点,__________________条直线与这条直线平行。
②如果两条直线都与第三条直线平行,那么这两条直线也互相________。
3.平行线的识别方法:
① ,两直线平行。
② ,两直线平行。
③ ,两直线平行。
④平行于同一条直线的两条直线 。
⑤垂直于同一条直线的两条直线 。
4.平行线的性质:
①两直线平行, 。
②两直线平行, 。
③两直线平行, 。
二.练习:
A组:
1.如图
= 1 \* GB3 ①如果∠1=∠2,那么 ∥
根据 。
②如果∠DAB+∠ABC=180 ,那么 ∥
根据 。
③如果∠3=∠B,那么 ∥
根据 。
2.如图A、B、C、D在同一直线上,AD∥EF,
①若∠E=58°,则∠1= ,
根据: ;
∠2= ,根据: 。
②若∠F=78°,则∠3= ,∠4= 。
3.如图,已知a∥b如果∠1=52 ,那么∠2= ,∠3= ,∠4= 。
4、如图(4)所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路 平行,若第一次拐角是150°,则第二次拐角为________.
B 组:
5.下列说法正确的是( )
(A)不相交的两条直线互相平行;
(B)同位角相等;
(C)同旁内角相等,两直线平行;
(D)在同一平面内,不平行的两条直线相交。
6.∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2的大小关系是( )
(A)∠1=∠2 (B)∠1>∠2
(C)∠1<∠2 (D)无法确定
7.如图,直线相交,∠1=120°,则∠2+∠3=( )
(A)60° (B)90°
(C)120° (D)180°
8.如图,要得到∥,则需要的条件是( )
(A)∠2=∠4 (B)∠1+∠3=180°
(C)∠1+∠2=180° (D)∠2=∠3
9.如图,AB∥EF,∠ECD=∠E,求证:CD∥AB。
证明:∵∠ECD=∠E,
∴EF∥ ,( )
∵AB∥EF,
∴CD∥AB( )
10、如图,a//b,c、d是截线,∠1=800,∠5=700,
求∠2、∠3、∠4的度数
11.如图:直线∥,∠3=85°,求∠1,∠2的度数。
12.如图,AB∥DE,BC∥EF,∠E=72°,求∠B的度数。
13.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,
问:①AC与BD平行吗?为什么?
②AE与BF平行吗?为什么?
C组:
如图,AB//CD,∠B=,∠BEC=,求∠C的度数。
第五章 相交线与平行线(十一)—平行线综合复习卷2
A 组:
一.填空:
1.如图,①当∠C=∠ ,时,AE∥DC,
根据 。
②当 ∥ 时,∠DAB+∠B=180°,
根据 。
2.如图,①若AD∥BC,则∠ =∠ ,
∠ =∠ ( )
②若∠ =∠ ,则AB∥DC,
根据
3.如图,①若∠1=∠2,则可以判定 ∥ ,
根据: 。
②若∠3=∠B,则可以判定 ∥ ,
根据: 。
③若∠4=∠F,则可以判定 ∥ 。
4.如图,已知直线AB∥CD,∠1=70°,那么∠2= °
5.如图,DE∥BC,若∠B=50°,则∠ADE= °;若∠C=75°,则∠DEC= °
二.解答题:
6.如图,已知∠1=∠2,求证:∠3=∠4。
7.如图,AB∥CD,AC与BD相交于E点,且∠B=25°,
求∠D的度数;
不用度量的方法,能否求得出∠C的度数?
B 组:
8.如图,AB⊥EF,CD⊥EF,∠α=∠F=45°,
则与∠FCD相等的角有( )个
(A) 1 (B) 2
(C) 3 (D) 4
9.如图,∥,∠1的度数是∠2的一半,则∠3等于( )
(A)60° (B)100°
(C)120° (D)130°
10.如图,AB∥ED,则∠A+∠C+∠D=( )
(A)180° (B)270°
(C)360° (D)540°
11.如图,AB∥CD,∠B=120°,
∠C=25°,则∠E= °
12.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?请说明理由。
13、已知:AB//CD,BD平分∠ABC,DB平分∠ADC,求证:DA//BC
14.如图,一张长方形纸条ABCD沿MN折叠后形成的图形,∠AMD=40°,求∠BNC 的度数。
SHAPE \* MERGEFORMAT
C组:
15.如图,∠1+∠2=180°,∠DAE=∠BCF,
AE与FC会平行吗?说明理由。
AD与BC的位置关系如何?为什么?
第五章 相交线和平行线( 十二)-------命题和定理
学习目标:了解命题、定理的概念
学习过程:
引例:观察下面几句话,回答问题
(1)我是初一的学生 (4)等式两边加上相同的数,结果仍是等式。
(2)对顶角相等 (5) 画∠AOB=300
(3)请把窗户关上 (6) 两条直线相交有几个交点?
上面几句话中,是对某件事情做出判断的语句有_____________
1、像这样________一件事情的语句,叫做___________,正确的命题成为______命题,错误的命题称为_________命题。
命题常可以写成“如果.........那么.........”的形式。
“如果”后接的部分是__________, “那么” 后接的部分是__________.
3、定理是从公理或其他真命题出发,用逻辑推理的方法判断得到的________
例1:判断下列语句是否是命题,并指出是真命题还是假命题
同角的余角相等 (2)不许大声说话 (3) 连接A、B两点
两点之间,线段最短 (5)等式两边加上相同的数,结果仍是等式。
对顶角不相等
命题是:_________________________________________
真命题是:______________________________________
假命题是:______________________________________
例2:写出下列命题的题设与结论
如果同旁内角互补,那么两直线平行.
题设是_____________________________________
结论是__________________________________________
“若”的题设是____________________,结论是________________
例3.把下列的命题改成“如果.........那么.........”的形式。
两直线平行,同旁内角互补.
___________________________________________________
对顶角相等
_________________________________________________
等角的补角相等.
__________________________________________________-
例4:命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举反例
四.练习
A组
1、判断下列语句是不是命题
(1)延长线段AB( )
(2)两条直线相交,只有一交点( )
(3)画线段AB的中点( )
(4)若|x|=2,则x=2( )
(5)角平分线是一条射线( )
2、分别指出下列各命题的题设和结论。
(1)如果a∥b,b∥c,那么a∥c
___________________________________
(2)内错角相等,两直线平行。
___________________________________
(3)如果,垂足为O,那么
___________________________________
3、分别把下列命题写成“如果……,那么……”的形式。
(1)垂直于同一条直线的两直线平行;
_______________________________________
(2)内错角相等。
________________________________________
B组
判断下列命题是真命题还是假命题,若是假命题,则举一个反例加以说明.
两个锐角的和是锐角;
答:该命题是_______命题 反例:
两条直线被第三条直线所截,内错角相等;
答:该命题是_______命题 反例:
两直线平行,同旁内角互补;
答:该命题是_______命题 反例:
互补的角是邻补角;
答:该命题是_______命题 反例:
2、选择题
(1)下列语句不是命题的是( )
A、两点之间,线段最短 B、不平行的两条直线有一个交点
C、x与y的和等于0吗? D、对顶角不相等。
(2)下列命题中真命题是( )
A、两个锐角之和为钝角 B、两个锐角之和为锐角
C、钝角大于它的补角 D、锐角小于它的余角
(3)命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等。其中假命题有( )
A、1个 B、2个 C、3个 D、4个
3、已知:如图AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF
证明:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2(已知)
∴∠ -∠ =∠ -∠ (等式性质)
∴∠_________=∠_________
∴BE∥CF( )
C组
4.如图,给出下列论断:(1)AB//DC;(2)AD//BC;(3)∠A=∠C,用上面其中两个作为题设,另一个作为结论,用”如果…….那么………”的形式写出一个你认为正确的命题,并加以证明.
第五章平行线和相交线(十三)——平移(1)
学习目标
通过具体实例认识平移变换,理解平移的基本内涵,理解平移前后两图形之间的关系,会找图形的对应点,对应角,对应线段,会画出平移后的图形。
学习过程
一、知识回顾
如图,看图填空
(1) ()
(2)
二、新课
1、观察下面的图案,它们有什么共同的特点?你能否想象出图案是如何绘制的
2、从以下生活中实例中你可以得出什么结论?
(1)传送带上的电视机移动方向从点移动到点、作___ 运动;
(2)传送带上的电视机的在运动前后大小形状没有发生改变,只是_ 改变了;
(3)如果电视机的屏幕沿AA’方向移动了4 m;那么电视机的其他部位(如电视的左上角)也沿方向移动移动了______ m;
3、我们使用直尺与三角尺画平行线时,我们把点A与点A′叫做对应点,把线段AB与线段A′B′叫做对应线段,∠A与∠A′叫做对应角.
此时:点B的对应点是点 ;点C的对应点是点 ;
线段AC的对应线段是线段 ;
线段BC的对应线段是线段 ;
∠B的对应角是 ;∠C的对应角是 .
△ABC平移的方向就是由点B到点B′的方向,
平移的距离就是线段 的长度.
平移的概念:我们把一个图形整体沿某一________移动一定______,会得到一个新的图形,.图形的这种运动叫做平移变换,简称平移.新图形的每一点,都是由原图形的某一点移动后得到的,这两个点称为对应点.
小结:
1、平移是由 和 所决定;
2、图形平移前后___ __和__ ___不变,只是__ ___变了;
3、平移前后两个图形对应线段 ,对应角 ;
例1、如图,把△ABC沿着射线NM方向平移到△A′B′C′,
则:点A的对应点是点 ;
线段AC的对应线段是线段 ,
∠C的对应角是 ,
平移的方向除了用射线NM方向表述外,
还可以表述为__________________
量出平移的距离为:
练习: A组
1、下面各图案中属于平移关系的是( )
A.(1)和(2) B.(1)和(3)
C.(1)和(4) D.(3)和(4)
2、下列运动中,属于物体平移的是 (填编号)
(1)大风车的转动; (2)电梯的升降; (3)火车在笔直的铁轨上行驶;
(4)飞机起飞前在跑道上加速滑行; (5)滑雪运动员在雪地上滑翔
3.下列现象是数学中的平移的是( )
A.冰化成水 B.电梯由一楼升到二楼
C.导弹击中目标后爆炸 D.卫星绕地球运动
4.在下面的六幅图中,(2)(3)(4)(5)(6)中的图案_________可以通过平移图案(1)得到的.
5、如图2的图案中,可以看出由图案自身的部分经过平移而得到的是( )
6.如图,△ABC平移后得到△DEF,已知∠B=35°,∠A=85°, AB=2cm,AC=1cm,
则,DE= cm。∠D= °∠F=______°
7.如图,△ABC平移到△A′B′C′的位置.
(1)方向是________________ ,
量出平移的距离是________.
(2)点D、E、F经过平移到了什么位置?
请将他们的对应点D′、E′、F′在
图上标出。
B组
1、 如图1,图形(1)沿射线XY平移后得到图形(2) 请在图形中标出点A和点B′的对应点、线段OC的对应线段。
2、如图2,小船经过平移到了新的位置,你发现缺少什么?请补上。
3、如图3,把图中多边形ABCD沿着箭头平移
6格,得到一个多边形,请画出此多边形,
并完成以下问题。
回答:
点A、D的对应点分别是:点 ;
线段BC、CA的对应线段分别是:线段 、 ;
∠A、∠C的对应角分别是:
4、如图4,将△ABC沿着箭头GH方向移动3cm得△DEF,画出△DEF
第五章平行线和相交线(十四)------平移(2)
学习目标:能按要求作出简单平面图形平移后的图形,掌握平移的特征,并会应用。
试一试:
如图, △ABC沿着PQ的方向平移到△A′B′C′的位置,连结对应点A A′,B B′,C C′,
对于它们的大小关系和位置关系,你有什么发现 写出你的结论.
归纳:
平移的特征:(1)图形的形状与大小 ;
(2)对应线段 ;
(3)对应角 ;
(4)对应点所连的线段 ;
例:如图,平移△ABC,使点A移动到点A′,
画出平移后的△A′B′C′.
练习
A组
一、选择题
1、下列A、B、C、D四幅图案中,能通过平移图案(1)得到的是( )
(1) A. B. C. D.
2、如图所示的图形中用其中一部分平移可以得到的是( )
3. 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
A. 先向下移动1格,再向左移动1格;
B. 先向下移动1格,再向左移动2格
C. 先向下移动2格,再向左移动1格;
D. 先向下移动2格,再向左移动2
4、如图所示的正方体的棱长为2cm,将线段AC
平移到A1C1的位置上,平移的距离是( )
A.1cm B.2cm
C.4cm D.无法求出
5、.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长; B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长; D.沿射线BD的方向移动DC长
二、解答题
1.如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对 应点D、点C的对应点F的位置.
2.如图,将方格纸中的小船先向左平移4倍,再向下平移5格,画出平移后的图形.
B组
一、填空
1.如图所示,平移△ABC可得到△DEF,如果∠A=50°,
∠C=60°,那么,∠EDF=_______度, ∠F=______度,
2.如图5长方形ABCD中,对角线AC与BD相交于O,DE∥AC,CE∥BD,那么△DCE可以看作是△________平移得到的,平移的距离是线
段________的长.
3.如图,在矩形ABCD中,AD=2AB,E、F分别为AD、BC的中点,扇形BFE、FCD的半径FB、CF的长度均为1cm,求阴影部分的面积为_______
二、解答题
1.如图,∠DEF是由∠ABC经过平移后得到的,DE交BC于G,若∠DGC=30°,求∠B的度数及∠E的度数.
三、利用如图所示的图形,通过平移设计美丽的图案
( http: / / )
C 组
1、如图、一个正方形毛巾的边长为30cm,上面横竖各有两道毛巾红条(红条外的其他部分为白色),宽度都是5cm,试求出此正放行毛巾的白色部分面积。
(反思:你想到了几种求解的方法?能利用平移的知识求解吗?)
第五章平行线和相交线(十五)——复习(1)
知识点回顾
一、邻补角与对顶角
邻补角的性质:邻补角__________; 对顶角的性质:对顶角_________
练习1、如图所示,∠1和∠2是对顶角的图形有( )毛
A B C D
2、如图所示,直线AB,CD,EF相交于点O,
(1) ∠AOD的对顶角是________,
∠EOC的对顶角是_________
(2)∠AOC的邻补角是_________________;∠EOB的邻补角是________________;
二、垂线的定义和性质
1、定义:几何语言:(正用)
(反用)
练习(1)、如图:,垂足为O,EF经过点O,
若 则
2、垂线的性质一:经过一点有且__________条直线和已知直线垂直.
练习(2)分别过点P作线段AB的垂线MN
3、点到直线的距离.
如图垂足为O,则线段_______的长度
叫作点到直线l的距离
垂线的性质二:垂线段_________.
练习
(1)(如图)AC⊥BC,CD⊥AB,AC=4,CB=3,AB=5,
C点到AB的距离是线段______的长度,
B点到AC的距离是________,
A点到BC的距离________,.
(2)计划把河水引到水池A中,可以先引______⊥CD,垂足为_____,
然后沿AB开渠,则能使所开的渠最短,
这样设计的依据是________________
三、相交线中的同位角,内错角,同旁内角
练习1、如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
(A)①、②、③ (B)①、②、④
(C)②、③、④ (D) ①、②、③、④
四、平行线的判定和性质
1、在同一平面内,与已知直线平行的直线有 条。
2、而经过直线外一点,与已知直线平行的直线有且只有 条。
3、平行于同一条直线的两条直线 。
练习1:如图:
(1)如果∠1=∠B,那么根据 ,可得AD∥BC。
(2)如果∠D=∠1,那么根据 ,可得AB∥CD。
(3)如果∠BAD+∠ABC=180 ,那么根据同旁内角互补,
两直线平行,可得 ∥ 。
(4)如果∠BCD+∠ABC=180 ,那么根据同旁内角互补,
两直线平行,可得 ∥
练习2:已知∠1=∠B,求证:∠2=∠C
证明:∵∠1=∠B(已知)
∴DE∥BC( )
∴∠2=∠C( )
五、命题
(1)下列句子中,__________是命题
①相等的角是对顶角 ②这两条直线平行吗 ③过A作直线的垂线 ④5x-x=2x
(2)把命题“同一平面内两条不平行的直线必相交”写成“如果……,那么……”的形式____________________________________________.
(3)”相等的角是对顶角”是____命题.(填”真””假”),并指出命题的
题设是_________________.结论是_____________________
六、平移
练习.如图,平移四边形ABCD到四边形EFGH,使得点C移到点G的位置,则有:
(1)对应线段AB= ,DA= ;对应线段BC∥ ,CD∥ ;
(2)对应角∠B= ,∠D= ;
(3)将图中所有对应点用虚线连结起来,得到的线段有 , , , ;
它们的关系是 。
练习A组:
1、过P作出OB、OA的垂线
2、AB∥DF,DE∥BC,∠1=65°求∠2、∠3的度数
3、已知,求的度数
C组
1、已知:如图 2-85,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,
求∠BOF度数.
第五章平行线和相交线(十六)——复习(2)
A 组
(一)、填空题
1. 如图1,直线AB和CD相交于点O,OE是∠DOB的平分线,若∠AOC=76°,则∠EOB=_______.
2.如图2,已知直线AB,CD相交于O,OE⊥AB,∠1=25°,
则∠2=_____度,∠3=_____度,∠4=______度.
3.如图3,OA⊥OB,OC⊥OD.若∠AOD=144°,则∠BOC=______.
4.如图4,AB∥CD、AF分别交AB、CD于A、C.CE平分∠DCF,
∠1=100,则∠2= .
5.如图,AB∥CD.若∠2是∠1的两倍,则∠2等于_______
(二)、选择题
1、下列命题中,是真命题的是( )
(A)相等的两个角是对顶角. (B)有公共顶点的两个角是对顶角.
(C)一条直线只有一条垂线. (D)过直线外一点有且只有一条直线垂直于已知直线.
2.如图,下列推理正确的是( )
(A)∵∠1=∠2,∴ AD∥BC (B)∵∠3=∠4,∴ AB∥CD
(C)∵∠3=∠5,∴ AB∥DC (D)∵∠3=∠5,∴ AD∥BC
3、如图,AB∥CD,AD∥BC,则下列各式中正确的是( )
A.∠1+∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3大小无关
(三)完成下列推理
1、如图,已知∠1=1350,∠8=450,直线a与b平行吗 说明理由:
(1)∵∠1=1350 (已知)
∴ ∠2=180°-∠____=_____
∴∠2=∠
∴ a∥b( )
(2)∵∠8=450(已知)
∴ ∠6=∠8=450 ( )
∴ + =1800
∴ a∥b ( );
2、如图,∠B=∠D,∠1=∠2.求证:AB∥CD.
【证明】∵ ∠1=∠2(已知),
∴ ∥ ( ),
∴ ∠DAB+∠ =180°( ).
∵ ∠B=∠D(已知),
∴ ∠DAB+∠ =180°( ),
∴ AB∥CD( ).
(四)证明
1、如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE
2、已知:如图,AD∥EF,∠1=∠2.求证:AB∥DG.
B组
五、证明
1、已知:如图2-82,DE∥BC,∠ADE=∠EFC,
求证:∠1=∠2
2、如图,已知AB∥CD,试再添上一个条件,使∠1=∠2成立(要求给出两个以上答案)
3、作∠AOB=90°,在OA上取一点C,使OC=3cm,在OB上取一点D,使OD=4cm,用三角尺过C点作OA的垂线,经过D点作OB的垂线,两条垂线相交于E
⑴量出∠CED的大小
⑵量出点E到OA的距离,点E到OB的距离
C组
1、画出一个边长为2cm的正方形,然后画出该正方形向北偏东30°方向平移4cm后的图形。
1
A
C
B
D
O
2
3
4
a
b
1
2
3
4
图1
A B C D
图2
图3
图4
图5
图6
图7
图8
图8
5
3
4
图2
图1
B
B
P
A
A
B
D
C
图1
图2
图1
图4
图3
图5
图6
图8
图7
图9
图(一)
图(二)
图(5)
图(6)
图4
图5
图6
图1
图2
图3
图4
图5
(3)
(2)
D
A
B
C
E
A
B
M
D
C
N
C
A
B
D
E
F
1
2
图2
图3
图4
A
B
C
D
O
A
D
E
B
C
1
2
A
D
F
B
E
C
1
2
3
D
E
A
B
C
2
1
C
D
F
E
B
A
1
2
- 1 -
