苏科新版2021-2022学年九年级上册数学《第3章 数据的集中趋势和离散程度》单元测试卷(word版含解析)
文档属性
| 名称 | 苏科新版2021-2022学年九年级上册数学《第3章 数据的集中趋势和离散程度》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科新版九年级上册数学《第3章 数据的集中趋势和离散程度》单元测试卷
一.选择题
1.若数据a1、a2、a3的平均数是3,则数据2a1、2a2、2a3的平均数是( )
A.2 B.3 C.4 D.6
2.若一组数据3、4、5、x、6、7的平均数是5,则x的值是( )
A.4 B.5 C.6 D.7
3.一组数据x1,x2,x3,x4,x5的平均数是x,另一组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是( )
A.x B.2x C.2x+5 D.10x+25
4.某中学为了解学生参加“青年大学习”网上班课的情况,对九年级6个班的学习人数进行了统计,得到各班参加班课的人数数据为5,10,10,12,14,9.对于这组数据,下列说法错误的是( )
A.平均数是10 B.众数是10 C.中位数是11 D.方差是
5.面试时,某人的基本知识、表达能力、工作态度的得分分别是90分、80分、85分,若依次按20%、40%、40%的比例确定成绩,则这个人的面试成绩是( )
A.82分 B.86分 C.85分 D.84分
6.一组数据:5、8、6、3、4的中位数是( )
A.5 B.6 C.4 D.8
7.利用科学计算器求一组数据的平均数,其按键顺序如下:
则输出结果为( )
A.1.5 B.6.75 C.2 D.7
8.为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如图统计图(每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A.中位数在60分~70分之间
B.中位数在70分~80分之间
C.中位数在80分~90分之间
D.中位数在90分~100分之间
9.按从小到大排列的一组数据:1,2,4,x,6,9,如果这组数据的中位数为5,那么这组数据的众数是( )
A.6 B.5.5 C.5 D.4
10.某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A.2.5 B.2 C.1 D.﹣2
二.填空题
11.长沙市某中学为积极响应“书香长沙,全民阅读”活动,助力学生良好阅读习惯的养成,形成浓厚的阅读氛围,随机调查了51名学生平均每天的阅读时间,统计结果如表所示,则在本次调查中,学生阅读时间的中位数是 .
时间(小时) 0.5 1 1.5 2 2.5
人数(人) 12 22 10 4 3
12.若一组数据4,9,5,m,3的平均数是5,则这组数据的众数是 .
13.若一组数据1,3,5,x的众数是3,则这组数据的方差为 .
14.若一组数据x1,x2,…,xn的平均数是a,方差是b,则4x1﹣3,4x2﹣3,…,4xn﹣3的平均数是 ,方差是 .
15.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是 .
16.某灯泡厂为测量一批灯泡的使用寿命,从中随机抽查了40只灯泡,它们的使用寿命如表所示,则这批灯泡的平均使用寿命是 h.
使用寿命x(h) 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200
灯泡只数 5 10 15 10
17.一组数据2,3,6,8,11的平均数是 .
18.若一组数据4,a,8,7,5的平均数是6,则这组数据的中位数是 .
19.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 .
20.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为 .
三.解答题
21.2019年12月13日是我国第六个南京大屠杀死难者公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
项目选手 演讲内容 演讲技巧 仪表形象
甲 95 90 85
乙 88 92 93
(1)如果根据三项成绩的平均分确定推荐人选,请通过计算说明甲、乙两人谁会被推荐.
(2)如果根据演讲内容、演讲技巧、仪表形象按5:4:1的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.
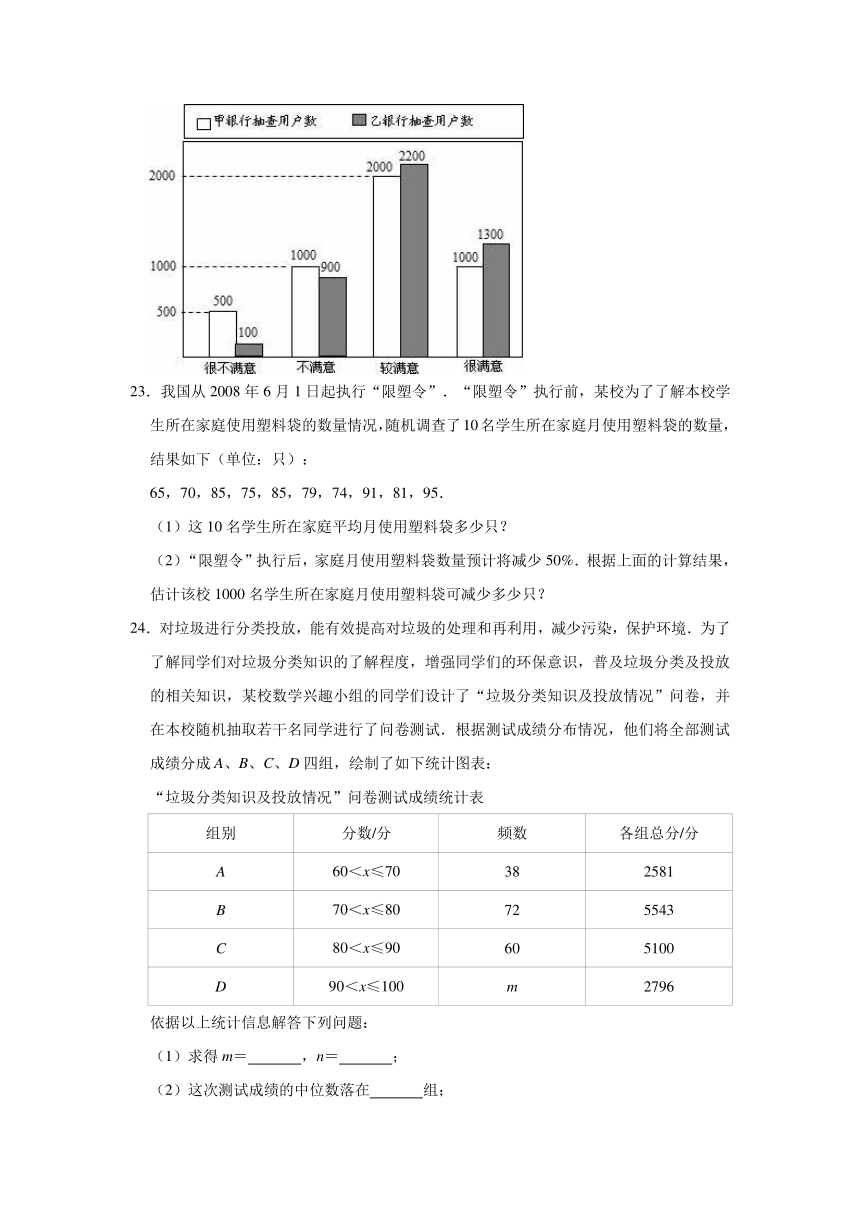
22.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
23.我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95.
(1)这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1000名学生所在家庭月使用塑料袋可减少多少只?
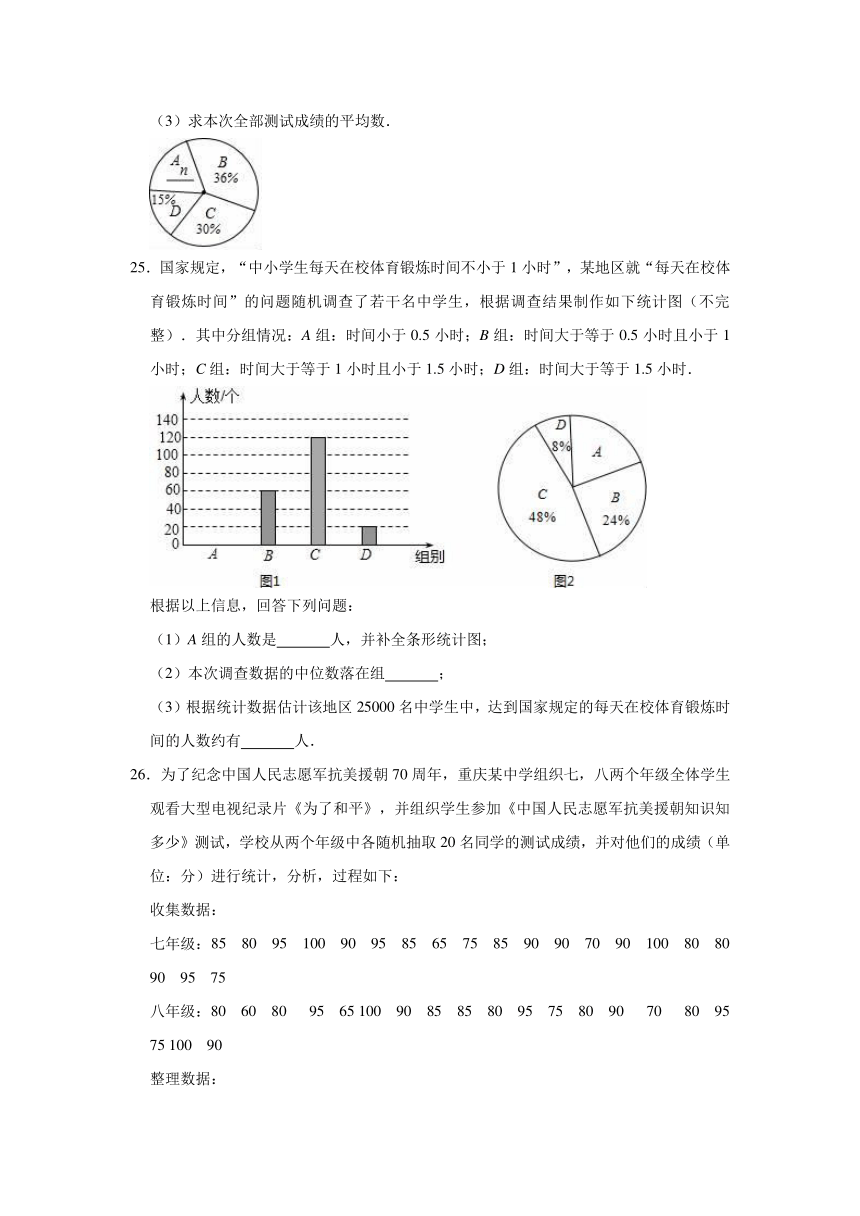
24.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别 分数/分 频数 各组总分/分
A 60<x≤70 38 2581
B 70<x≤80 72 5543
C 80<x≤90 60 5100
D 90<x≤100 m 2796
依据以上统计信息解答下列问题:
(1)求得m= ,n= ;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
25.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 人.
26.为了纪念中国人民志愿军抗美援朝70周年,重庆某中学组织七,八两个年级全体学生观看大型电视纪录片《为了和平》,并组织学生参加《中国人民志愿军抗美援朝知识知多少》测试,学校从两个年级中各随机抽取20名同学的测试成绩,并对他们的成绩(单位:分)进行统计,分析,过程如下:
收集数据:
七年级:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
八年级:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据:
成绩x(分) 60<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 5 8 5
八年级 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
七年级 85.75 a 90
八年级 83.5 82.5 b
应用数据:
(1)请直接写出上述表中a= ,b= ;
(2)根据以上数据,你认为该校七,八年级中哪个年级学生观看完纪录片后对抗美援朝知识了解情况更好?请说明理由(写出一条理由即可);
(3)该校七,八年级共2000名学生参与作答,估计成绩大于90分的学生人数共有多少人?
27.为贯彻实施新修订的《义务教育法》,某市2006﹣2007学年对全市六个乡镇农村学生实行免除学杂费,由政府财政补助,总额达2 016万元,如图是根据该市农村学生人数情况制成的条形统计图.
(1)该市农村学生平均每人免除学杂费多少元?
(2)该市农村学生人数约占全市学生人数的70%.若下学年该市学生总数及城乡学生人数比例不变,要将此惠民政策在全市实施,估计政府财政补助共需多少万元?(注:本题城市和农村学生均指义务教育阶段学生)
参考答案与试题解析
一.选择题
1.解:∵数据a1、a2、a3的平均数是3,
∴a1+a2+a3=9,
∴(2a1+2a2+2a3)÷3=18÷3=6,
故选:D.
2.解:由题意(3+4+5+x+6+7)=5,
解得x=5,
故选:B.
3.解:这组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是:
(2x1+5+2x2+5+2x3+5+2x4+5+2x5+5)÷5
=[(2x1+2x2+2x3+2x4+2x5)+(5+5+5+5+5)]÷5
=[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5
根据x1,x2,x3,x4,x5的平均数是x,
∴(x1+x2+x3+x4+x5)÷5=x,
∴x1+x2+x3+x4+x5=5x,
把x1+x2+x3+x4+x5=5x代入[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5得;
=(10x+25)÷5,
=2x+5.
故选:C.
4.解:A、平均数是(5+10+10+12+14+9)÷6=10,故本选项说法正确,不符合题意;
B、∵10出现了2次,出现的次数最多,∴众数是10,故本选项说法正确,不符合题意;
C、把这些数从小到大排列为:5,9,10,10,12,14,则中位数是=10,故本选项说法错误,符合题意;
D、方差为:×[(5﹣10)2+2×(10﹣10)2+(12﹣10)2+(14﹣10)2+(9﹣10)2]=,故本选项说法正确,不符合题意;
故选:C.
5.解:根据题意得:
90×20%+80×40%+85×40%=84(分);
故选:D.
6.解:从小到大排列此数据为:3、4、5、6、8,最中间的数是5,
故中位数是5.
故选:A.
7.解:(3+3+0+2)÷4
=8÷4
=2
∴输出结果为2.
故选:C.
8.解:调查总人数为:30+90+90+60=270(人),
将这270人的得分从小到大排列后,处在第135、136位的两个数都落在80~90分之间,
因此中位数在80分~90分之间.
故选:C.
9.解:∵这组数据按从小到大排列为1,2,4,x,6,9,
又∵这组数据的中位数为5,
∴(4+x)÷2=5,
解得:x=6,
∴这组数据为1,2,4,6,6,9,
∴这组数据的众数为6;
故选:A.
10.解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是﹣=﹣2;
故选:D.
二.填空题
11.解:∵一共调查了51名学生平均每天的阅读时间,
∴中位数应为第26个数,
而第26个数是1,
∴中位数是1.
故答案为:1.
12.解:∵数据4,9,5,m,3的平均数是5,
∴4+9+5+m+3=5×5,
解得m=4,
则这组数据为4,9,5,4,3,
∴这组数据的众数为4,
故答案为:4.
13.解:∵数据1,3,5,x的众数是3,
∴x=3,
则数据为1、3、3、5,
∴这组数据的平均数为=3,
∴这组数据的方差为×[(1﹣3)2+2×(3﹣3)2+(5﹣3)2]=2,
故答案为:2.
14.解:∵x1、x2…xn的平均数是a,
∴(x1、x2…xn)÷n=a
∴(4x1﹣3,4x2﹣3…4xn﹣3)÷4=4×a﹣3=4a﹣3,
∵x1、x2…xn的方差是b,
∴4x1﹣3,4x2﹣3…4xn﹣3的方差是4×4×b=16b.
答案为:4a﹣3;16b.
15.解:∵x1,x2,x3,x4的平均数为5
∴x1+x2+x3+x4=4×5=20,
∴x1+3,x2+3,x3+3,x4+3的平均数为:
=(x1+3+x2+3+x3+3+x4+3)÷4
=(20+12)÷4
=8,
故答案为:8.
16.解:根据题意得:(800×5+1200×10+1600×15+2000×10)=×60000=1500(h);
则这批灯泡的平均使用寿命是1500h.
故答案为:1500.
17.解:(2+3+6+8+11)÷5
=30÷5
=6
所以一组数据2,3,6,8,11的平均数是6.
故答案为:6.
18.解:由题意得4+a+8+7+5=6×5,
解得:a=6,
这组数据按照从小到大的顺序排列为:4,5,6,7,8,
则中位数为6.
故答案为:6.
19.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
20.解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
三.解答题
21.解:(1)(分),
(分),
∵90<91,
∴乙将被推荐参加校级决赛.
(2)(分),
(分),
∵92>90.1,
∴甲将被推荐参加校级决赛.
建议:由于演讲内容的权较大,乙这项得成绩较低,应改进演讲内容,争取更好得成绩.
答案不唯一,只要合理都可.
22.解:(1)甲银行的用户满意度分数的众数为2;乙银行的用户满意度分数的中位数为2;
(2)甲银行抽查用户数为:500+1000+2000+1000=4500(户),
乙银行抽查用户数为:100+900+2200+1300=4500(户).
所以甲银行满意度分数的平均值=(500×0+1000×1+2000×2+1000×4)=2(分),
乙银行满意度分数的平均值=(100×0+900×1+2200×2+1300×4)=(分).
答:甲、乙两银行用户满意度分数的平均值分别为2分,分;
(3)因为乙银行用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙银行的用户满意度较高.
23.解:(1)平均数=(65+70+85+75+85+79+74+91+81+95)=80(只).
答:这10名学生所在家庭平均月使用塑料袋80只.
(2)80×1000×50%=40000.
答:执行“限塑令”后,估计1000名学生所在家庭月使用塑料袋可减少40000只.
24.解:(1)∵被调查的学生总人数为72÷36%=200人,
∴m=200﹣(38+72+60)=30,n=×100%=19%,
故答案为:30、19%;
(2)∵共有200个数据,其中第100、101个数据均落在B组,
∴中位数落在B组,
故答案为:B;
(3)本次全部测试成绩的平均数为=80.1(分).
25.解:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
故答案为:50,补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
故答案为:C;
(3)由题意可得,
该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
故答案为:14000.
26.解:(1)将七年级成绩重新排列为:65、70、75、75、80、80、80、85、85、85、90、90、90、90、90、95、95、95、100、100,
七年级成绩的中位数a==87.5,八年级众数b=80,
故答案为:87.5,80;
(2)七年级观看完纪录片后对抗美援朝知识了解情况更好,
因为七年级成绩的平均数、众数和中位数均大于八年级;
(3)估计成绩大于90分的学生人数共有2000×=500(人).
27.解:(1)2016÷(0.8+1.4+0.7+0.6+1.1+1.0)=360(元);
(2)(1﹣70%)×(5.6÷70%)×360+2016=2880(万元).
一.选择题
1.若数据a1、a2、a3的平均数是3,则数据2a1、2a2、2a3的平均数是( )
A.2 B.3 C.4 D.6
2.若一组数据3、4、5、x、6、7的平均数是5,则x的值是( )
A.4 B.5 C.6 D.7
3.一组数据x1,x2,x3,x4,x5的平均数是x,另一组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是( )
A.x B.2x C.2x+5 D.10x+25
4.某中学为了解学生参加“青年大学习”网上班课的情况,对九年级6个班的学习人数进行了统计,得到各班参加班课的人数数据为5,10,10,12,14,9.对于这组数据,下列说法错误的是( )
A.平均数是10 B.众数是10 C.中位数是11 D.方差是
5.面试时,某人的基本知识、表达能力、工作态度的得分分别是90分、80分、85分,若依次按20%、40%、40%的比例确定成绩,则这个人的面试成绩是( )
A.82分 B.86分 C.85分 D.84分
6.一组数据:5、8、6、3、4的中位数是( )
A.5 B.6 C.4 D.8
7.利用科学计算器求一组数据的平均数,其按键顺序如下:
则输出结果为( )
A.1.5 B.6.75 C.2 D.7
8.为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如图统计图(每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A.中位数在60分~70分之间
B.中位数在70分~80分之间
C.中位数在80分~90分之间
D.中位数在90分~100分之间
9.按从小到大排列的一组数据:1,2,4,x,6,9,如果这组数据的中位数为5,那么这组数据的众数是( )
A.6 B.5.5 C.5 D.4
10.某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A.2.5 B.2 C.1 D.﹣2
二.填空题
11.长沙市某中学为积极响应“书香长沙,全民阅读”活动,助力学生良好阅读习惯的养成,形成浓厚的阅读氛围,随机调查了51名学生平均每天的阅读时间,统计结果如表所示,则在本次调查中,学生阅读时间的中位数是 .
时间(小时) 0.5 1 1.5 2 2.5
人数(人) 12 22 10 4 3
12.若一组数据4,9,5,m,3的平均数是5,则这组数据的众数是 .
13.若一组数据1,3,5,x的众数是3,则这组数据的方差为 .
14.若一组数据x1,x2,…,xn的平均数是a,方差是b,则4x1﹣3,4x2﹣3,…,4xn﹣3的平均数是 ,方差是 .
15.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是 .
16.某灯泡厂为测量一批灯泡的使用寿命,从中随机抽查了40只灯泡,它们的使用寿命如表所示,则这批灯泡的平均使用寿命是 h.
使用寿命x(h) 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200
灯泡只数 5 10 15 10
17.一组数据2,3,6,8,11的平均数是 .
18.若一组数据4,a,8,7,5的平均数是6,则这组数据的中位数是 .
19.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 .
20.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为 .
三.解答题
21.2019年12月13日是我国第六个南京大屠杀死难者公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
项目选手 演讲内容 演讲技巧 仪表形象
甲 95 90 85
乙 88 92 93
(1)如果根据三项成绩的平均分确定推荐人选,请通过计算说明甲、乙两人谁会被推荐.
(2)如果根据演讲内容、演讲技巧、仪表形象按5:4:1的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.
22.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
23.我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95.
(1)这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1000名学生所在家庭月使用塑料袋可减少多少只?
24.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别 分数/分 频数 各组总分/分
A 60<x≤70 38 2581
B 70<x≤80 72 5543
C 80<x≤90 60 5100
D 90<x≤100 m 2796
依据以上统计信息解答下列问题:
(1)求得m= ,n= ;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
25.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 人.
26.为了纪念中国人民志愿军抗美援朝70周年,重庆某中学组织七,八两个年级全体学生观看大型电视纪录片《为了和平》,并组织学生参加《中国人民志愿军抗美援朝知识知多少》测试,学校从两个年级中各随机抽取20名同学的测试成绩,并对他们的成绩(单位:分)进行统计,分析,过程如下:
收集数据:
七年级:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
八年级:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据:
成绩x(分) 60<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 5 8 5
八年级 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
七年级 85.75 a 90
八年级 83.5 82.5 b
应用数据:
(1)请直接写出上述表中a= ,b= ;
(2)根据以上数据,你认为该校七,八年级中哪个年级学生观看完纪录片后对抗美援朝知识了解情况更好?请说明理由(写出一条理由即可);
(3)该校七,八年级共2000名学生参与作答,估计成绩大于90分的学生人数共有多少人?
27.为贯彻实施新修订的《义务教育法》,某市2006﹣2007学年对全市六个乡镇农村学生实行免除学杂费,由政府财政补助,总额达2 016万元,如图是根据该市农村学生人数情况制成的条形统计图.
(1)该市农村学生平均每人免除学杂费多少元?
(2)该市农村学生人数约占全市学生人数的70%.若下学年该市学生总数及城乡学生人数比例不变,要将此惠民政策在全市实施,估计政府财政补助共需多少万元?(注:本题城市和农村学生均指义务教育阶段学生)
参考答案与试题解析
一.选择题
1.解:∵数据a1、a2、a3的平均数是3,
∴a1+a2+a3=9,
∴(2a1+2a2+2a3)÷3=18÷3=6,
故选:D.
2.解:由题意(3+4+5+x+6+7)=5,
解得x=5,
故选:B.
3.解:这组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是:
(2x1+5+2x2+5+2x3+5+2x4+5+2x5+5)÷5
=[(2x1+2x2+2x3+2x4+2x5)+(5+5+5+5+5)]÷5
=[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5
根据x1,x2,x3,x4,x5的平均数是x,
∴(x1+x2+x3+x4+x5)÷5=x,
∴x1+x2+x3+x4+x5=5x,
把x1+x2+x3+x4+x5=5x代入[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5得;
=(10x+25)÷5,
=2x+5.
故选:C.
4.解:A、平均数是(5+10+10+12+14+9)÷6=10,故本选项说法正确,不符合题意;
B、∵10出现了2次,出现的次数最多,∴众数是10,故本选项说法正确,不符合题意;
C、把这些数从小到大排列为:5,9,10,10,12,14,则中位数是=10,故本选项说法错误,符合题意;
D、方差为:×[(5﹣10)2+2×(10﹣10)2+(12﹣10)2+(14﹣10)2+(9﹣10)2]=,故本选项说法正确,不符合题意;
故选:C.
5.解:根据题意得:
90×20%+80×40%+85×40%=84(分);
故选:D.
6.解:从小到大排列此数据为:3、4、5、6、8,最中间的数是5,
故中位数是5.
故选:A.
7.解:(3+3+0+2)÷4
=8÷4
=2
∴输出结果为2.
故选:C.
8.解:调查总人数为:30+90+90+60=270(人),
将这270人的得分从小到大排列后,处在第135、136位的两个数都落在80~90分之间,
因此中位数在80分~90分之间.
故选:C.
9.解:∵这组数据按从小到大排列为1,2,4,x,6,9,
又∵这组数据的中位数为5,
∴(4+x)÷2=5,
解得:x=6,
∴这组数据为1,2,4,6,6,9,
∴这组数据的众数为6;
故选:A.
10.解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是﹣=﹣2;
故选:D.
二.填空题
11.解:∵一共调查了51名学生平均每天的阅读时间,
∴中位数应为第26个数,
而第26个数是1,
∴中位数是1.
故答案为:1.
12.解:∵数据4,9,5,m,3的平均数是5,
∴4+9+5+m+3=5×5,
解得m=4,
则这组数据为4,9,5,4,3,
∴这组数据的众数为4,
故答案为:4.
13.解:∵数据1,3,5,x的众数是3,
∴x=3,
则数据为1、3、3、5,
∴这组数据的平均数为=3,
∴这组数据的方差为×[(1﹣3)2+2×(3﹣3)2+(5﹣3)2]=2,
故答案为:2.
14.解:∵x1、x2…xn的平均数是a,
∴(x1、x2…xn)÷n=a
∴(4x1﹣3,4x2﹣3…4xn﹣3)÷4=4×a﹣3=4a﹣3,
∵x1、x2…xn的方差是b,
∴4x1﹣3,4x2﹣3…4xn﹣3的方差是4×4×b=16b.
答案为:4a﹣3;16b.
15.解:∵x1,x2,x3,x4的平均数为5
∴x1+x2+x3+x4=4×5=20,
∴x1+3,x2+3,x3+3,x4+3的平均数为:
=(x1+3+x2+3+x3+3+x4+3)÷4
=(20+12)÷4
=8,
故答案为:8.
16.解:根据题意得:(800×5+1200×10+1600×15+2000×10)=×60000=1500(h);
则这批灯泡的平均使用寿命是1500h.
故答案为:1500.
17.解:(2+3+6+8+11)÷5
=30÷5
=6
所以一组数据2,3,6,8,11的平均数是6.
故答案为:6.
18.解:由题意得4+a+8+7+5=6×5,
解得:a=6,
这组数据按照从小到大的顺序排列为:4,5,6,7,8,
则中位数为6.
故答案为:6.
19.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
20.解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
三.解答题
21.解:(1)(分),
(分),
∵90<91,
∴乙将被推荐参加校级决赛.
(2)(分),
(分),
∵92>90.1,
∴甲将被推荐参加校级决赛.
建议:由于演讲内容的权较大,乙这项得成绩较低,应改进演讲内容,争取更好得成绩.
答案不唯一,只要合理都可.
22.解:(1)甲银行的用户满意度分数的众数为2;乙银行的用户满意度分数的中位数为2;
(2)甲银行抽查用户数为:500+1000+2000+1000=4500(户),
乙银行抽查用户数为:100+900+2200+1300=4500(户).
所以甲银行满意度分数的平均值=(500×0+1000×1+2000×2+1000×4)=2(分),
乙银行满意度分数的平均值=(100×0+900×1+2200×2+1300×4)=(分).
答:甲、乙两银行用户满意度分数的平均值分别为2分,分;
(3)因为乙银行用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙银行的用户满意度较高.
23.解:(1)平均数=(65+70+85+75+85+79+74+91+81+95)=80(只).
答:这10名学生所在家庭平均月使用塑料袋80只.
(2)80×1000×50%=40000.
答:执行“限塑令”后,估计1000名学生所在家庭月使用塑料袋可减少40000只.
24.解:(1)∵被调查的学生总人数为72÷36%=200人,
∴m=200﹣(38+72+60)=30,n=×100%=19%,
故答案为:30、19%;
(2)∵共有200个数据,其中第100、101个数据均落在B组,
∴中位数落在B组,
故答案为:B;
(3)本次全部测试成绩的平均数为=80.1(分).
25.解:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
故答案为:50,补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
故答案为:C;
(3)由题意可得,
该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
故答案为:14000.
26.解:(1)将七年级成绩重新排列为:65、70、75、75、80、80、80、85、85、85、90、90、90、90、90、95、95、95、100、100,
七年级成绩的中位数a==87.5,八年级众数b=80,
故答案为:87.5,80;
(2)七年级观看完纪录片后对抗美援朝知识了解情况更好,
因为七年级成绩的平均数、众数和中位数均大于八年级;
(3)估计成绩大于90分的学生人数共有2000×=500(人).
27.解:(1)2016÷(0.8+1.4+0.7+0.6+1.1+1.0)=360(元);
(2)(1﹣70%)×(5.6÷70%)×360+2016=2880(万元).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
