湘教新版2021-2022学年九年级上册数学《第4章 锐角三角函数》单元测试卷(word版含解析)
文档属性
| 名称 | 湘教新版2021-2022学年九年级上册数学《第4章 锐角三角函数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 19:59:21 | ||
图片预览




文档简介
2021-2022学年湘教新版九年级上册数学《第4章 锐角三角函数》单元测试卷
一.选择题
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
2.在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值( )
A.也扩大3倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
3.Rt△ABC中,∠C=90°,若BC=2,AC=3,下列各式中正确的是 ( )
A. B. C. D.
4.若cosA=,则下列结论正确的为( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
5.已知tanα=1,那么的值等于( )
A. B. C.1 D.
6.在Rt△ABC中,∠C=90°,若cosA=,则sinB的值是( )
A. B. C. D.
7.在Rt△ABC中,已知∠ACB=90°,BC=1,AB=2,那么下列结论正确的是( )
A.sinA= B.tanA= C.cosB= D.cotB=
8.在Rt△ABC中,∠C=90°,若a=3,b=4,则sinB的值为( )
A. B. C. D.
9.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是( )
A.b=c cosB B.b=a tanB C.b=c sinB D.a=b tanA
10.在Rt△ABC中,∠ACB=90°,AB=,tanB=2,则AC的长为( )
A.1 B.2 C. D.
二.填空题
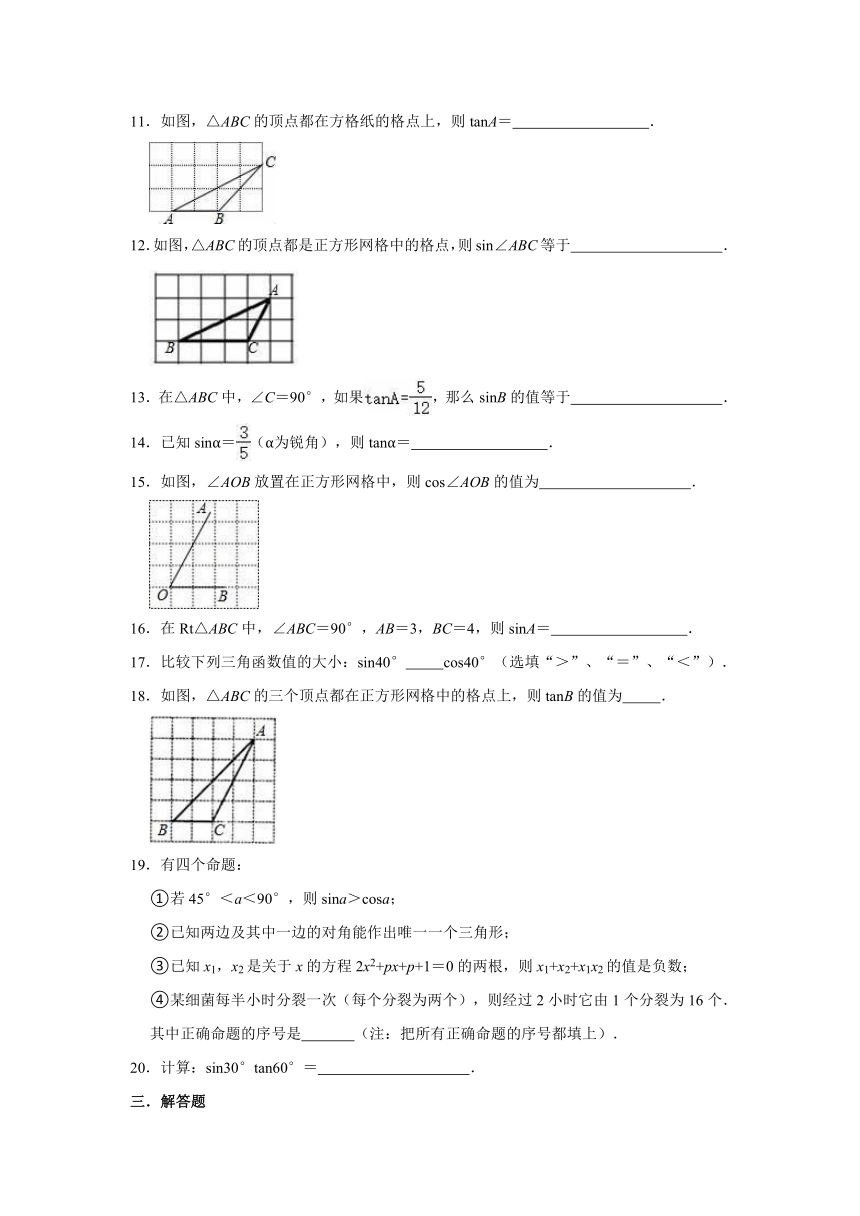
11.如图,△ABC的顶点都在方格纸的格点上,则tanA= .
12.如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于 .
13.在△ABC中,∠C=90°,如果,那么sinB的值等于 .
14.已知sinα=(α为锐角),则tanα= .
15.如图,∠AOB放置在正方形网格中,则cos∠AOB的值为 .
16.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA= .
17.比较下列三角函数值的大小:sin40° cos40°(选填“>”、“=”、“<”).
18.如图,△ABC的三个顶点都在正方形网格中的格点上,则tanB的值为 .
19.有四个命题:
①若45°<a<90°,则sina>cosa;
②已知两边及其中一边的对角能作出唯一一个三角形;
③已知x1,x2是关于x的方程2x2+px+p+1=0的两根,则x1+x2+x1x2的值是负数;
④某细菌每半小时分裂一次(每个分裂为两个),则经过2小时它由1个分裂为16个.
其中正确命题的序号是 (注:把所有正确命题的序号都填上).
20.计算:sin30°tan60°= .
三.解答题
21.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
22.有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30°.
(1)请直接写出AF的长;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求△AFK的面积(保留根号).
23.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,﹣2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标.
24.已知a,b,c是△ABC的三边,a,b,c满足等式b2=(c+a)(c﹣a),且5b﹣4c=0,求sinA+sinB的值.
25.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
26.在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a,b是关于x的一元二次方程x2﹣mx+2m﹣2=0的两个根,求Rt△ABC中较小锐角的正弦值.
参考答案与试题解析
一.选择题
1.解:设BC=x,则AB=3x,
由勾股定理得,AC==2x,
则tanB==2,
故选:A.
2.解:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选:C.
3.解:∵∠C=90°,BC=2,AC=3,
∴AB=,
A.sinA===,故此选项错误;
B.cosA==,故此选项错误;
C.tanA==,故此选项正确;
D.cotA==,故此选项错误.
故选:C.
4.解:∵cos30°=≈0.866,cos45°=≈0.707,cosA==0.75,
又∵0.866>0.75>0.707,
∴30°<A<45°.
故选:B.
5.解:由于tanα==1,
∴原式====.
故选:A.
6.解:在△ABC中,∠C=90°,∠A+∠B=90°,
则sinB=cosA=.
故选:A.
7.解:如图所示:
∵∠ACB=90°,BC=1,AB=2,
∴AC=,
∴sinA=,故选项A错误;
tanA==,故选项B错误;
cosB=,故选项C错误;
cotB=,正确.
故选:D.
8.解:由勾股定理可知:c=5,
∴sinB==,
故选:A.
9.解:在Rt△ABC中,∠C=90°,
则tanA=,
tanB=,cosB=,tanB=;
因而b=c sinB=a tanB,
a=b tanA,
错误的是b=c cosB.
故选:A.
10.解:在Rt△ABC中,∠ACB=90°,tanB=2,
∴=2,
∴BC=AC,
由勾股定理得,AB2=AC2+BC2,即()2=AC2+(AC)2,
解得,AC=2,
故选:B.
二.填空题
11.解:如图,△ACD中,∵∠ADC=90°,CD=2,AD=4,
∴tanA===.
故答案为.
12.解:∵AB所在的直角三角形的两边分别为:2,4,
∴AB==2.
∴sin∠ABC==.
13.解:如图,∵,
∴设AC=12k,BC=5k,
则AB==13k,
∴sinB===.
故答案为:.
14.解:∵sin2α+cos2α=1,
∴cosα==,
∴tanα===,
故答案为:.
15.解:将∠AOB放在一直角三角形中,邻边为1,对边为2,由勾股定理得斜边,
则cos∠AOB的值==.
16.解:∵在Rt△ABC中,∠ABC=90°,AB=3,BC=4,
∴AC==5(勾股定理).
∴sinA==.
故答案是:.
17.解:∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40°.
18.解:如图,
在△ABD中,AD=4,BD=4,
则tanB==1.
故答案为1.
19.解:①因为sin45°=cos45°=,再结合锐角三角函数的变化规律,故此选项正确;
②不一定能够判定两个三角形全等,故此选项错误;
③根据根与系数的关系,得x1+x2=﹣,x1x2=.
∴x1+x2+x1x2=,是正数.
故此选项错误;
④根据题意,得2小时它由1个分裂24个,即16个,故此选项正确.
故正确的有①④.
20.解:sin30°tan60°=×=.
故答案为:.
三.解答题
21.解:∵tan∠A==,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B===.
22.解:(1)AF=;
(2)△AFK为等腰三角形时,分两种情况:
①当AK=FK时,如图.过点K作KN⊥AF于N,则KN⊥AF,AN=NF=AF=2cm.
在直角△NFK中,∠KNF=90°,∠F=30°,
∴KN=NF tan∠F=2cm.
∴△AFK的面积=×AF×KN=;
②当AF=FK时,如图.过点K作KP⊥AF于P.
在直角△PFK中,∠KPF=90°,∠F=30°,
∴KP=KF=2cm.
∴△AFK的面积=×AF×KP=12cm2.
23.解:(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,BA=2,
∴tan∠BOA===. (3分)
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4). (5分)
(3)△O′A′B′如图所示,O′(﹣2,﹣4),A′(2,﹣4).(8分)
24.解:∵b2=(c+a)(c﹣a),
∴b2=c2﹣a2,
即:a2+b2=c2,
∴△ABC是以c为斜边的Rt△ABC,
∵5b﹣4c=0,∴,
设b=4k,则c=5k,
∴△ABC中,a=3k,
∴sinA+sinB==.
25.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
26.解:∵a,b是方程x2﹣mx+2m﹣2=0的解,
∴a+b=m,ab=2m﹣2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2﹣2ab,c=5,
∴a2+b2=(a+b)2﹣2ab=25,
即:m2﹣2(2m﹣2)=25
解得,m1=7,m2=﹣3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=﹣3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2﹣7x+12=0,
解得,x1=3,x2=4,
不妨设a=3,则sinA==,
∴Rt△ABC中较小锐角的正弦值为.
一.选择题
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
2.在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值( )
A.也扩大3倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
3.Rt△ABC中,∠C=90°,若BC=2,AC=3,下列各式中正确的是 ( )
A. B. C. D.
4.若cosA=,则下列结论正确的为( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
5.已知tanα=1,那么的值等于( )
A. B. C.1 D.
6.在Rt△ABC中,∠C=90°,若cosA=,则sinB的值是( )
A. B. C. D.
7.在Rt△ABC中,已知∠ACB=90°,BC=1,AB=2,那么下列结论正确的是( )
A.sinA= B.tanA= C.cosB= D.cotB=
8.在Rt△ABC中,∠C=90°,若a=3,b=4,则sinB的值为( )
A. B. C. D.
9.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列关系中错误的是( )
A.b=c cosB B.b=a tanB C.b=c sinB D.a=b tanA
10.在Rt△ABC中,∠ACB=90°,AB=,tanB=2,则AC的长为( )
A.1 B.2 C. D.
二.填空题
11.如图,△ABC的顶点都在方格纸的格点上,则tanA= .
12.如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于 .
13.在△ABC中,∠C=90°,如果,那么sinB的值等于 .
14.已知sinα=(α为锐角),则tanα= .
15.如图,∠AOB放置在正方形网格中,则cos∠AOB的值为 .
16.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA= .
17.比较下列三角函数值的大小:sin40° cos40°(选填“>”、“=”、“<”).
18.如图,△ABC的三个顶点都在正方形网格中的格点上,则tanB的值为 .
19.有四个命题:
①若45°<a<90°,则sina>cosa;
②已知两边及其中一边的对角能作出唯一一个三角形;
③已知x1,x2是关于x的方程2x2+px+p+1=0的两根,则x1+x2+x1x2的值是负数;
④某细菌每半小时分裂一次(每个分裂为两个),则经过2小时它由1个分裂为16个.
其中正确命题的序号是 (注:把所有正确命题的序号都填上).
20.计算:sin30°tan60°= .
三.解答题
21.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
22.有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30°.
(1)请直接写出AF的长;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求△AFK的面积(保留根号).
23.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,﹣2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标.
24.已知a,b,c是△ABC的三边,a,b,c满足等式b2=(c+a)(c﹣a),且5b﹣4c=0,求sinA+sinB的值.
25.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
26.在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a,b是关于x的一元二次方程x2﹣mx+2m﹣2=0的两个根,求Rt△ABC中较小锐角的正弦值.
参考答案与试题解析
一.选择题
1.解:设BC=x,则AB=3x,
由勾股定理得,AC==2x,
则tanB==2,
故选:A.
2.解:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选:C.
3.解:∵∠C=90°,BC=2,AC=3,
∴AB=,
A.sinA===,故此选项错误;
B.cosA==,故此选项错误;
C.tanA==,故此选项正确;
D.cotA==,故此选项错误.
故选:C.
4.解:∵cos30°=≈0.866,cos45°=≈0.707,cosA==0.75,
又∵0.866>0.75>0.707,
∴30°<A<45°.
故选:B.
5.解:由于tanα==1,
∴原式====.
故选:A.
6.解:在△ABC中,∠C=90°,∠A+∠B=90°,
则sinB=cosA=.
故选:A.
7.解:如图所示:
∵∠ACB=90°,BC=1,AB=2,
∴AC=,
∴sinA=,故选项A错误;
tanA==,故选项B错误;
cosB=,故选项C错误;
cotB=,正确.
故选:D.
8.解:由勾股定理可知:c=5,
∴sinB==,
故选:A.
9.解:在Rt△ABC中,∠C=90°,
则tanA=,
tanB=,cosB=,tanB=;
因而b=c sinB=a tanB,
a=b tanA,
错误的是b=c cosB.
故选:A.
10.解:在Rt△ABC中,∠ACB=90°,tanB=2,
∴=2,
∴BC=AC,
由勾股定理得,AB2=AC2+BC2,即()2=AC2+(AC)2,
解得,AC=2,
故选:B.
二.填空题
11.解:如图,△ACD中,∵∠ADC=90°,CD=2,AD=4,
∴tanA===.
故答案为.
12.解:∵AB所在的直角三角形的两边分别为:2,4,
∴AB==2.
∴sin∠ABC==.
13.解:如图,∵,
∴设AC=12k,BC=5k,
则AB==13k,
∴sinB===.
故答案为:.
14.解:∵sin2α+cos2α=1,
∴cosα==,
∴tanα===,
故答案为:.
15.解:将∠AOB放在一直角三角形中,邻边为1,对边为2,由勾股定理得斜边,
则cos∠AOB的值==.
16.解:∵在Rt△ABC中,∠ABC=90°,AB=3,BC=4,
∴AC==5(勾股定理).
∴sinA==.
故答案是:.
17.解:∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40°.
18.解:如图,
在△ABD中,AD=4,BD=4,
则tanB==1.
故答案为1.
19.解:①因为sin45°=cos45°=,再结合锐角三角函数的变化规律,故此选项正确;
②不一定能够判定两个三角形全等,故此选项错误;
③根据根与系数的关系,得x1+x2=﹣,x1x2=.
∴x1+x2+x1x2=,是正数.
故此选项错误;
④根据题意,得2小时它由1个分裂24个,即16个,故此选项正确.
故正确的有①④.
20.解:sin30°tan60°=×=.
故答案为:.
三.解答题
21.解:∵tan∠A==,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B===.
22.解:(1)AF=;
(2)△AFK为等腰三角形时,分两种情况:
①当AK=FK时,如图.过点K作KN⊥AF于N,则KN⊥AF,AN=NF=AF=2cm.
在直角△NFK中,∠KNF=90°,∠F=30°,
∴KN=NF tan∠F=2cm.
∴△AFK的面积=×AF×KN=;
②当AF=FK时,如图.过点K作KP⊥AF于P.
在直角△PFK中,∠KPF=90°,∠F=30°,
∴KP=KF=2cm.
∴△AFK的面积=×AF×KP=12cm2.
23.解:(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,BA=2,
∴tan∠BOA===. (3分)
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4). (5分)
(3)△O′A′B′如图所示,O′(﹣2,﹣4),A′(2,﹣4).(8分)
24.解:∵b2=(c+a)(c﹣a),
∴b2=c2﹣a2,
即:a2+b2=c2,
∴△ABC是以c为斜边的Rt△ABC,
∵5b﹣4c=0,∴,
设b=4k,则c=5k,
∴△ABC中,a=3k,
∴sinA+sinB==.
25.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
26.解:∵a,b是方程x2﹣mx+2m﹣2=0的解,
∴a+b=m,ab=2m﹣2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2﹣2ab,c=5,
∴a2+b2=(a+b)2﹣2ab=25,
即:m2﹣2(2m﹣2)=25
解得,m1=7,m2=﹣3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=﹣3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2﹣7x+12=0,
解得,x1=3,x2=4,
不妨设a=3,则sinA==,
∴Rt△ABC中较小锐角的正弦值为.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
