湘教新版2021-2022学年七年级上册数学《第4章 图形的认识》单元测试卷(word版含解析)
文档属性
| 名称 | 湘教新版2021-2022学年七年级上册数学《第4章 图形的认识》单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览




文档简介
2021-2022学年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷
一.选择题
1.下列几何体中,属于棱柱的有( )
A.6个 B.5个 C.4个 D.3个
2.下列图形中属于棱柱的有( )
A.2个 B.3个 C.4个 D.5个
3.观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来( )
A. B. C. D.
4.直线AB,线段CD,射线EF的位置如图所示,下图中不可能相交的是( )
A. B.
C. D.
5.木工师傅在锯木板时,往往先在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线
D.经过已知直线外一点,有且只有一条直线与已知直线平行
6.如图,AB=12cm,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度是( )
A.4cm B.6cm C.8cm D.10cm
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.则该模型对应的立体图形可能是( )
A.三棱柱 B.三棱锥 C.圆锥 D.圆柱
8.下面四个几何图形中,表示平面图形是( )
A. B. C. D.
9.下列四个生产生活现象,可以用“两点之间线段最短”来解释的是( )
A.用两颗钉子可以把木条固定在墙上
B.在高速公路的建设中,通常从大山中开挖隧道穿过,把道路取直,以缩短路程
C.植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上
D.打靶的时候,眼睛要与枪上的准星、靶心在同一直线上
10.已知三点M、N、G,画直线MN、画射线MG、连接NG,按照上述语句画图正确的是( )
A. B.
C. D.
二.填空题
11.一个直棱柱有12个顶点,所有侧棱长的和为72cm,则每条侧棱长为 cm.
12.火车往返于A、B两个城市,中途经过4个站点(共6个站点),不同的车站来往需要不同的车票,共有 种不同的车票.
13.平面上有五条直线相交(没有互相平行的),则这五条直线最多有 个交点,最少有 个交点.
14.已知圆柱的底面积为60cm2,高为4cm,则这个圆柱体积为 cm3.
15.已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,…,由此可以推测n棱柱有 个面, 个顶点, 条棱.
16.把一个长方形卷起来,可卷成 个不同圆柱的侧面.
17.将一根细木条固定在墙上,至少需要两根钉子,理由: .
18.数轴上有两点M、N,点M到点E的距离为2,点N到点E距离为6,则M、N之间的距离为 .
19.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 (填图形名称).
20.如图,在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短.你认为 同学的说法是正确的.
三.解答题
21.如图所示为8个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
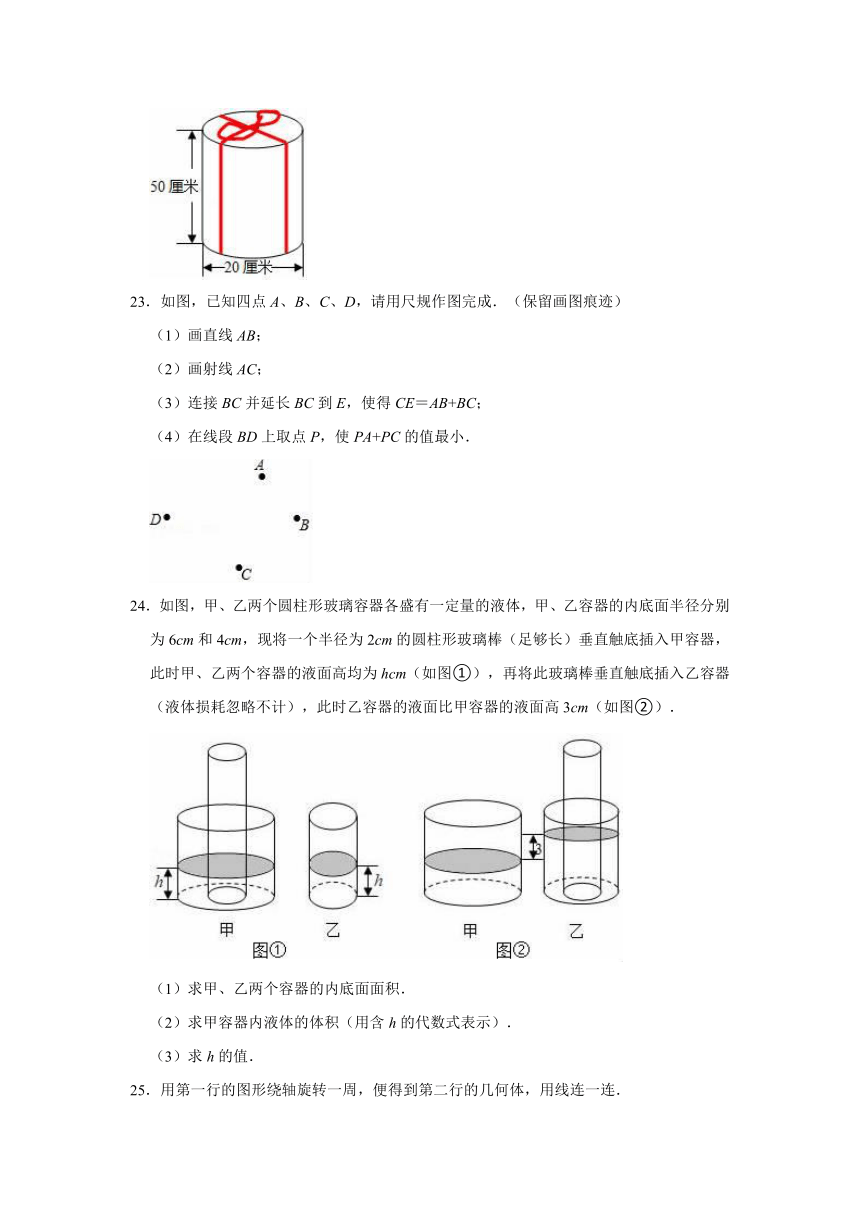
22.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
23.如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
24.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
25.用第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
26.如图,平面上有四个点A、B、C、D,根据下列语句画图:
(1)画线段AB;
(2)连接CD,并将其反向延长至E,使得DE=2CD;
(3)在平面内找到一点F,使F到A、B、C、D四点距离最短.
27.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
参考答案与试题解析
一.选择题
1.解:根据棱柱的定义可得:符合棱柱定义的有第一、三、六个几何体都是棱柱,共三个.
故选:D.
2.解:根据棱柱的定义可得:符合棱柱定义的有第一、二、六、七个几何体都是棱柱,共4个.
故选:C.
3.解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:D.
4.解:A选项中,直线AB与线段CD无交点,符合题意;
B选项中,直线AB与射线EF有交点,不合题意;
C选项中,线段CD与射线EF有交点,不合题意;
D选项中,直线AB与射线EF有交点,不合题意;
故选:A.
5.解:在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是两点确定一条直线.
故选:A.
6.解:∵AB=12cm,C为AB的中点,
∴AC=BC=AB=6cm,
∵AD:CB=1:3,
∴AD=2cm,
∴DC=AC﹣AD=4cm,
∴DB=DC+BC=10cm,
故选:D.
7.解:侧面是曲面,底面是圆形,该模型对应的立体图形可能是圆锥,
故选:C.
8.解:前三个是立体图形,即圆锥体、圆柱体、正方体,只有D选项是三角形,是平面图形,
故选:D.
9.解:A、用两颗钉子可以把木条固定在墙上,根据两点确定一条直线,故本选项不符合题意;
B、在高速公路的建设中,通常从大山中开挖隧道穿过,把道路取直,以缩短路程,根据两点之间,线段最短,故本选项符合题意;
C、植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上,根据两点确定一条直线,故本选项不符合题意;
D、打靶的时候,眼睛要与枪上的准星、靶心在同一直线上,根据两点确定一条直线,故本选项不符合题意;
故选:B.
10.解:画直线MN、画射线MG、连接MG,如图所示:
故选:B.
二.填空题
11.解:∵一个直棱柱有12个顶点,
∴该棱柱是六棱柱,
∴它的每条侧棱长=72÷6=12cm.
故答案为:12.
12.解:如图:,
车票:AC、CD、DE、EF、FB、AD、AE、AF、AB、CE、CF、CB、DF、DB、EB,BE、BD、FD、BC、FC、EC、BA、FA、EA、DA、BF、FE、ED、DC、CA.
火车往返于A、B两个城市,中途经过4个站点(共6个站点),不同的车站来往需要不同的车票,共有30种不同的车票,
故答案为:30.
13.解:最多时=10,
相交于同一个点时最少,有1个交点.
14.解:V=S h=60×4=240(cm3).
故答案为:240.
15.解:n棱柱有(n+2)个面,2n个顶点,3n条棱.
故答案为:n+2、2n、3n.
16.解:把一个长方形卷起来,可卷成2个不同圆柱的侧面.
17.解:在墙上固定一根木条至少需要两根钉子,依据的数学道理是两点确定一条直线.
故答案为:两点确定一条直线.
18.解:当E在线段MN上时,MN=ME+NE=2+6=8.
当E在线段MN的反向延长线上时,MN=NE﹣ME=6﹣2=4,
综上所述:MN=8,MN=4,
故答案为:8,4.
19.解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
20.解:在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,
喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短.你认为 喜羊羊同学的说法是正确的,
故答案为:喜羊羊.
三.解答题
21.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
22.解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
23.解:如图所画:
(1)
(2)
(3)
(4).
24.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
25.解:图(1)旋转一周形成一个圆柱与一个圆锥的组合体,即B;图(2)旋转一周形成圆锥,即D;图(3)旋转一周形成圆柱,即A;图(4)旋转一周形成半球,即C.
(1)─B,
(2)─D,
(3)─A,
(4)─C.
26.解:(1)线段AB即为所求;
(2)如图所示:DE=2DC;
(3)如图所示:F点即为所求.
27.解:(1)
图 a b c d
顶点数(S) 4 7 8 10
边数(M) 6 9 12 15
区域数(N) 3 3 5 6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
一.选择题
1.下列几何体中,属于棱柱的有( )
A.6个 B.5个 C.4个 D.3个
2.下列图形中属于棱柱的有( )
A.2个 B.3个 C.4个 D.5个
3.观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来( )
A. B. C. D.
4.直线AB,线段CD,射线EF的位置如图所示,下图中不可能相交的是( )
A. B.
C. D.
5.木工师傅在锯木板时,往往先在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线
D.经过已知直线外一点,有且只有一条直线与已知直线平行
6.如图,AB=12cm,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度是( )
A.4cm B.6cm C.8cm D.10cm
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.则该模型对应的立体图形可能是( )
A.三棱柱 B.三棱锥 C.圆锥 D.圆柱
8.下面四个几何图形中,表示平面图形是( )
A. B. C. D.
9.下列四个生产生活现象,可以用“两点之间线段最短”来解释的是( )
A.用两颗钉子可以把木条固定在墙上
B.在高速公路的建设中,通常从大山中开挖隧道穿过,把道路取直,以缩短路程
C.植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上
D.打靶的时候,眼睛要与枪上的准星、靶心在同一直线上
10.已知三点M、N、G,画直线MN、画射线MG、连接NG,按照上述语句画图正确的是( )
A. B.
C. D.
二.填空题
11.一个直棱柱有12个顶点,所有侧棱长的和为72cm,则每条侧棱长为 cm.
12.火车往返于A、B两个城市,中途经过4个站点(共6个站点),不同的车站来往需要不同的车票,共有 种不同的车票.
13.平面上有五条直线相交(没有互相平行的),则这五条直线最多有 个交点,最少有 个交点.
14.已知圆柱的底面积为60cm2,高为4cm,则这个圆柱体积为 cm3.
15.已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,…,由此可以推测n棱柱有 个面, 个顶点, 条棱.
16.把一个长方形卷起来,可卷成 个不同圆柱的侧面.
17.将一根细木条固定在墙上,至少需要两根钉子,理由: .
18.数轴上有两点M、N,点M到点E的距离为2,点N到点E距离为6,则M、N之间的距离为 .
19.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 (填图形名称).
20.如图,在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短.你认为 同学的说法是正确的.
三.解答题
21.如图所示为8个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
22.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
23.如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
24.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
25.用第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
26.如图,平面上有四个点A、B、C、D,根据下列语句画图:
(1)画线段AB;
(2)连接CD,并将其反向延长至E,使得DE=2CD;
(3)在平面内找到一点F,使F到A、B、C、D四点距离最短.
27.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
参考答案与试题解析
一.选择题
1.解:根据棱柱的定义可得:符合棱柱定义的有第一、三、六个几何体都是棱柱,共三个.
故选:D.
2.解:根据棱柱的定义可得:符合棱柱定义的有第一、二、六、七个几何体都是棱柱,共4个.
故选:C.
3.解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:D.
4.解:A选项中,直线AB与线段CD无交点,符合题意;
B选项中,直线AB与射线EF有交点,不合题意;
C选项中,线段CD与射线EF有交点,不合题意;
D选项中,直线AB与射线EF有交点,不合题意;
故选:A.
5.解:在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是两点确定一条直线.
故选:A.
6.解:∵AB=12cm,C为AB的中点,
∴AC=BC=AB=6cm,
∵AD:CB=1:3,
∴AD=2cm,
∴DC=AC﹣AD=4cm,
∴DB=DC+BC=10cm,
故选:D.
7.解:侧面是曲面,底面是圆形,该模型对应的立体图形可能是圆锥,
故选:C.
8.解:前三个是立体图形,即圆锥体、圆柱体、正方体,只有D选项是三角形,是平面图形,
故选:D.
9.解:A、用两颗钉子可以把木条固定在墙上,根据两点确定一条直线,故本选项不符合题意;
B、在高速公路的建设中,通常从大山中开挖隧道穿过,把道路取直,以缩短路程,根据两点之间,线段最短,故本选项符合题意;
C、植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上,根据两点确定一条直线,故本选项不符合题意;
D、打靶的时候,眼睛要与枪上的准星、靶心在同一直线上,根据两点确定一条直线,故本选项不符合题意;
故选:B.
10.解:画直线MN、画射线MG、连接MG,如图所示:
故选:B.
二.填空题
11.解:∵一个直棱柱有12个顶点,
∴该棱柱是六棱柱,
∴它的每条侧棱长=72÷6=12cm.
故答案为:12.
12.解:如图:,
车票:AC、CD、DE、EF、FB、AD、AE、AF、AB、CE、CF、CB、DF、DB、EB,BE、BD、FD、BC、FC、EC、BA、FA、EA、DA、BF、FE、ED、DC、CA.
火车往返于A、B两个城市,中途经过4个站点(共6个站点),不同的车站来往需要不同的车票,共有30种不同的车票,
故答案为:30.
13.解:最多时=10,
相交于同一个点时最少,有1个交点.
14.解:V=S h=60×4=240(cm3).
故答案为:240.
15.解:n棱柱有(n+2)个面,2n个顶点,3n条棱.
故答案为:n+2、2n、3n.
16.解:把一个长方形卷起来,可卷成2个不同圆柱的侧面.
17.解:在墙上固定一根木条至少需要两根钉子,依据的数学道理是两点确定一条直线.
故答案为:两点确定一条直线.
18.解:当E在线段MN上时,MN=ME+NE=2+6=8.
当E在线段MN的反向延长线上时,MN=NE﹣ME=6﹣2=4,
综上所述:MN=8,MN=4,
故答案为:8,4.
19.解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
20.解:在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,
喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短.你认为 喜羊羊同学的说法是正确的,
故答案为:喜羊羊.
三.解答题
21.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
22.解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
23.解:如图所画:
(1)
(2)
(3)
(4).
24.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
25.解:图(1)旋转一周形成一个圆柱与一个圆锥的组合体,即B;图(2)旋转一周形成圆锥,即D;图(3)旋转一周形成圆柱,即A;图(4)旋转一周形成半球,即C.
(1)─B,
(2)─D,
(3)─A,
(4)─C.
26.解:(1)线段AB即为所求;
(2)如图所示:DE=2DC;
(3)如图所示:F点即为所求.
27.解:(1)
图 a b c d
顶点数(S) 4 7 8 10
边数(M) 6 9 12 15
区域数(N) 3 3 5 6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
同课章节目录
