苏科版八年级数学上册 2.2 轴对称的性质(课件)
文档属性
| 名称 | 苏科版八年级数学上册 2.2 轴对称的性质(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 759.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 07:22:42 | ||
图片预览




文档简介
(共19张PPT)
2.2 轴对称的性质
复习回顾:
什么叫做两个图形成轴对称?
把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就称这两个图形关于这条直线对称,也称这两个图形成轴对称.
复习回顾:
什么叫做轴对称图形?
把一个图形沿某一条直线翻折,如果直线两旁的部分能互相重合,那么这个图形叫轴对称图形。
根据“轴对称”的定义,如果两个图形成轴对称,那么这两个图形能够完全重合,
即成轴对称的两个图形
全等
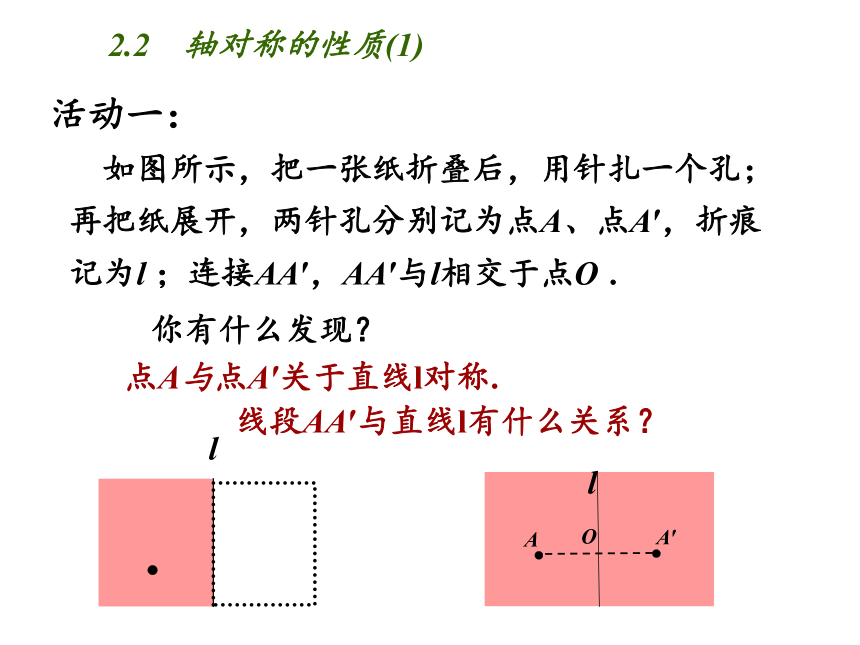
如图所示,把一张纸折叠后,用针扎一个孔;再把纸展开,两针孔分别记为点A、点A′,折痕记为l ;连接AA′,AA′与l相交于点O .
你有什么发现?
l
活动一:
A
●
l
●
A′
O
●
2.2 轴对称的性质(1)
点A与点A′关于直线l对称.
线段AA′与直线l有什么关系?
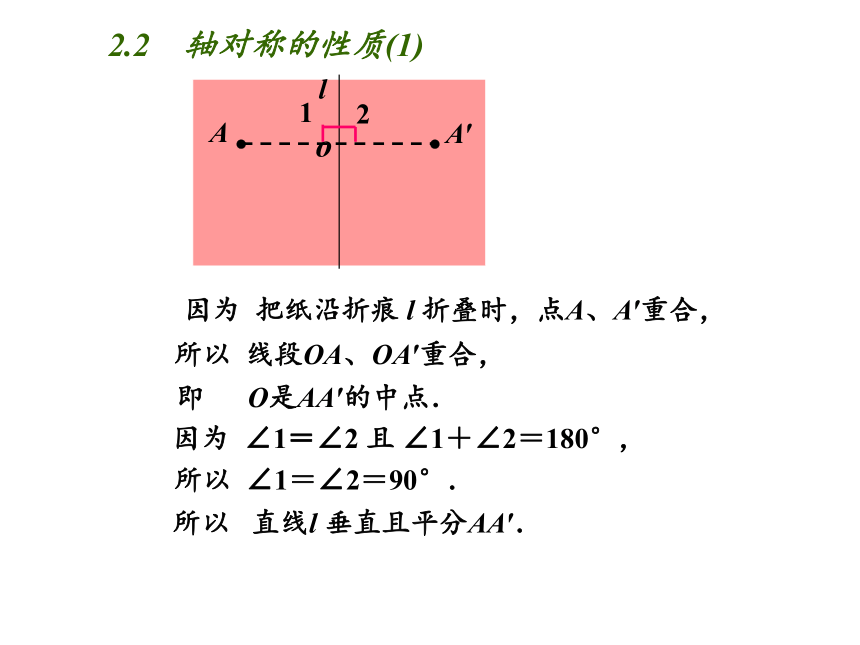
所以 线段OA、OA′重合,
因为 ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
所以 ∠1=∠2=90°.
l
A
A′
●
●
2
o
1
所以 直线l 垂直且平分AA′.
因为 把纸沿折痕 l 折叠时,点A、A′重合,
2.2 轴对称的性质(1)
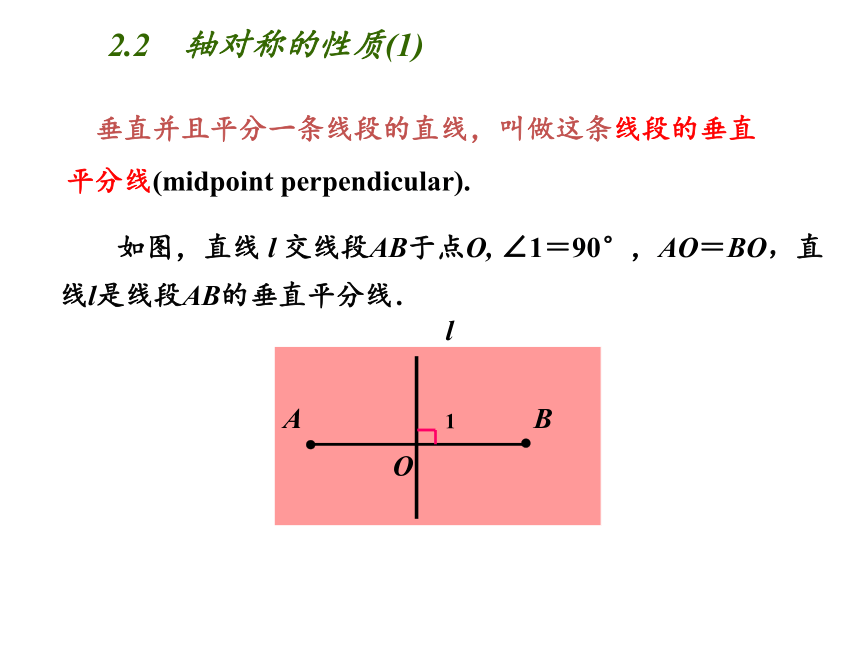
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线(midpoint perpendicular).
l
如图,直线 l 交线段AB于点O, ∠1=90°,AO=BO,直线l是线段AB的垂直平分线.
B
A
●
●
1
O
2.2 轴对称的性质(1)
仿照上面的操作,在对折后的纸上再扎一个孔,把纸展开后记这两个针孔为点B、点B′,连接AB、A′B′、BB′.你有什么新的发现?
A′
B′
l
活动二:
2.2 轴对称的性质(1)
如图,并仿照上面进行操作,扎孔、展开、标记、连线.
△ABC 与△A′B′C′有什么关系?
你能得出什么结论?
A
C
B
A′
B′
●
C′
l
活动三:
2.2 轴对称的性质(1)
1.成轴对称的两个图形全等.
2.成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
轴对称的性质:
说一说
轴对称的性质
A
A
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
例1 小明取一张纸,用小针在纸上扎出“4”,然后将纸放在镜子前.
(1)图中两个“4”有什么关系?
(1)你能画出镜子所在直线l的位置吗?
l
方法(1)
方法(2)
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(2)图中点A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CAB= ,∠ACD= .
E、G、F、H
EF、EG
FH
∠FEG
∠EFH
2.2 轴对称的性质(1)
(3)连接AE、BG, AE与BG平行吗?为什么?
∵ A和E,B和G是关于直线 l 的对称点,
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
∴ l⊥AE ,l⊥BG.
∴ AE ∥BG.
解:(3)平行.
2.2 轴对称的性质(1)
1
2
∴ ∠1=∠2=90°.
(4) AE与BG平行,能说明轴对称图形对称点的连线一定互相平行吗?
解:(4) 不一定.
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
如图,对称点的连线DH、CF就不互相平行,而是在同一条直线上,
从而说成轴对称图形对称点的连线互相平行或在同一条直线上.
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(5)延长线段CA、FE,连接CB、FG并延长,作直线AB、EG,你有什么发现吗?
轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行.
2.2 轴对称的性质(1)
回顾与思考:
通过本节课的学习,你有什么收获?
还有哪些疑惑?
2.2 轴对称的性质(1)
小结
(1)成轴对称的两个图形全等.
(2)如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线.
轴对称的性质:
2.2 轴对称的性质(1)
谢 谢
2.2 轴对称的性质
复习回顾:
什么叫做两个图形成轴对称?
把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就称这两个图形关于这条直线对称,也称这两个图形成轴对称.
复习回顾:
什么叫做轴对称图形?
把一个图形沿某一条直线翻折,如果直线两旁的部分能互相重合,那么这个图形叫轴对称图形。
根据“轴对称”的定义,如果两个图形成轴对称,那么这两个图形能够完全重合,
即成轴对称的两个图形
全等
如图所示,把一张纸折叠后,用针扎一个孔;再把纸展开,两针孔分别记为点A、点A′,折痕记为l ;连接AA′,AA′与l相交于点O .
你有什么发现?
l
活动一:
A
●
l
●
A′
O
●
2.2 轴对称的性质(1)
点A与点A′关于直线l对称.
线段AA′与直线l有什么关系?
所以 线段OA、OA′重合,
因为 ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
所以 ∠1=∠2=90°.
l
A
A′
●
●
2
o
1
所以 直线l 垂直且平分AA′.
因为 把纸沿折痕 l 折叠时,点A、A′重合,
2.2 轴对称的性质(1)
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线(midpoint perpendicular).
l
如图,直线 l 交线段AB于点O, ∠1=90°,AO=BO,直线l是线段AB的垂直平分线.
B
A
●
●
1
O
2.2 轴对称的性质(1)
仿照上面的操作,在对折后的纸上再扎一个孔,把纸展开后记这两个针孔为点B、点B′,连接AB、A′B′、BB′.你有什么新的发现?
A′
B′
l
活动二:
2.2 轴对称的性质(1)
如图,并仿照上面进行操作,扎孔、展开、标记、连线.
△ABC 与△A′B′C′有什么关系?
你能得出什么结论?
A
C
B
A′
B′
●
C′
l
活动三:
2.2 轴对称的性质(1)
1.成轴对称的两个图形全等.
2.成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
轴对称的性质:
说一说
轴对称的性质
A
A
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
例1 小明取一张纸,用小针在纸上扎出“4”,然后将纸放在镜子前.
(1)图中两个“4”有什么关系?
(1)你能画出镜子所在直线l的位置吗?
l
方法(1)
方法(2)
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(2)图中点A、B、C、D的对称点分别是 ,线段AC、AB的对应线段分别是 ,CD= , ∠CAB= ,∠ACD= .
E、G、F、H
EF、EG
FH
∠FEG
∠EFH
2.2 轴对称的性质(1)
(3)连接AE、BG, AE与BG平行吗?为什么?
∵ A和E,B和G是关于直线 l 的对称点,
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
∴ l⊥AE ,l⊥BG.
∴ AE ∥BG.
解:(3)平行.
2.2 轴对称的性质(1)
1
2
∴ ∠1=∠2=90°.
(4) AE与BG平行,能说明轴对称图形对称点的连线一定互相平行吗?
解:(4) 不一定.
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
如图,对称点的连线DH、CF就不互相平行,而是在同一条直线上,
从而说成轴对称图形对称点的连线互相平行或在同一条直线上.
2.2 轴对称的性质(1)
●
●
●
●
A
D
C
B
●
●
●
●
F
E
H
G
l
(5)延长线段CA、FE,连接CB、FG并延长,作直线AB、EG,你有什么发现吗?
轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行.
2.2 轴对称的性质(1)
回顾与思考:
通过本节课的学习,你有什么收获?
还有哪些疑惑?
2.2 轴对称的性质(1)
小结
(1)成轴对称的两个图形全等.
(2)如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线.
轴对称的性质:
2.2 轴对称的性质(1)
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
