苏科版八年级数学上册 6.1 函数(课件)(共27张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 6.1 函数(课件)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
6.1 函数
如果在一个变化过程中,有两个变量,如x和y,对于x的每一个值,y都有唯一的值与之对应,那么我们称y是x的___.其中x是_____.
在某一变化过程中,可以取不同数值的量,叫做_____.还有一种量,它的取值始终保持不变,称之为____.
你还记得吗
变量
常量
自变量
函数
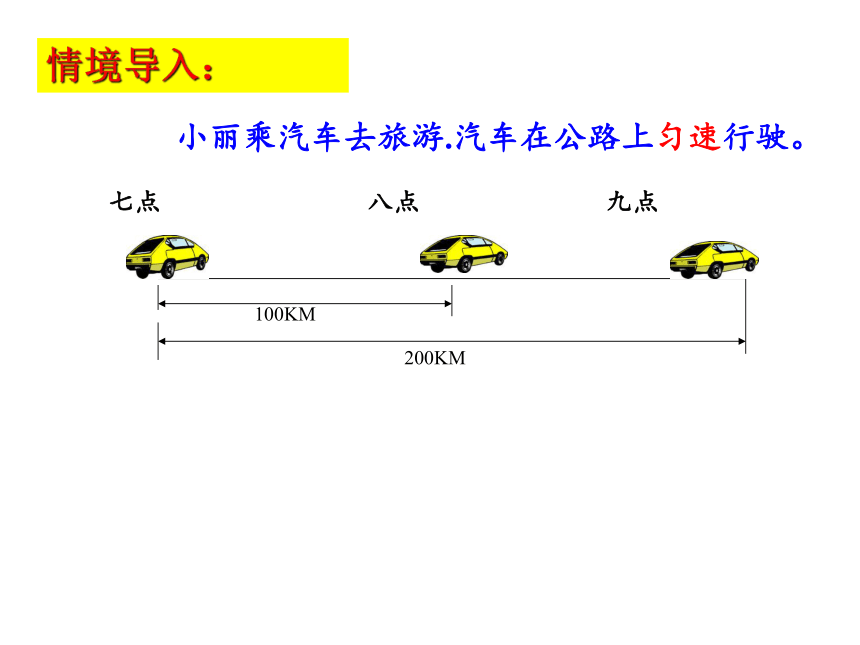
七点 八点 九点
100KM
200KM
情境导入:
小丽乘汽车去旅游.汽车在公路上匀速行驶。
汽车以100km/h的速度匀速行驶,在这一变化过程中,
(1)有哪些变量?哪些常量?
(2)变量之间是函数关系吗?为什么?
(3)若汽车行驶的时间为t(h),汽车行驶的路程为y(km).怎样表示函数y与自变量t的关系?
1.可以列表表示:
t / h 1 2 3 4 5 t
y / km
100
200
300
400
500
100t
在汽车以100km/h的速度匀速行驶,这一变化过程中:
把自变量t的一系列值和函数y的对应值列成一个表,这种表示函数关系的方法是列表法.
在汽车以100km/h的速度匀速行驶,这一变化过程中:
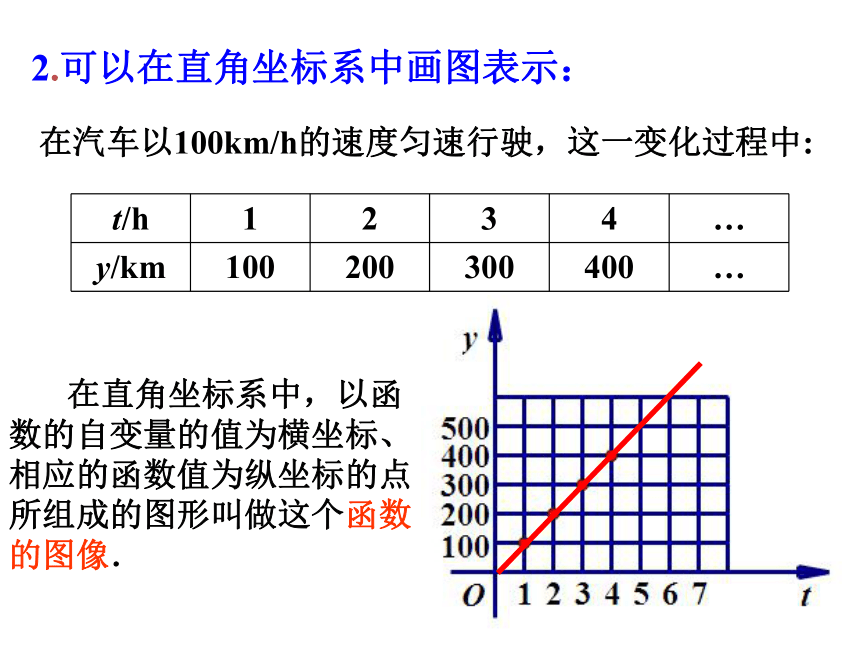
t/h 1 2 3 4 …
y/km 100 200 300 400 …
在直角坐标系中,以函数的自变量的值为横坐标、相应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
2.可以在直角坐标系中画图表示:
像y=100t 、S=6n+2等表示两个变量之间关系的式子称为函数表达式.
3.可以列式表示:
y=100t
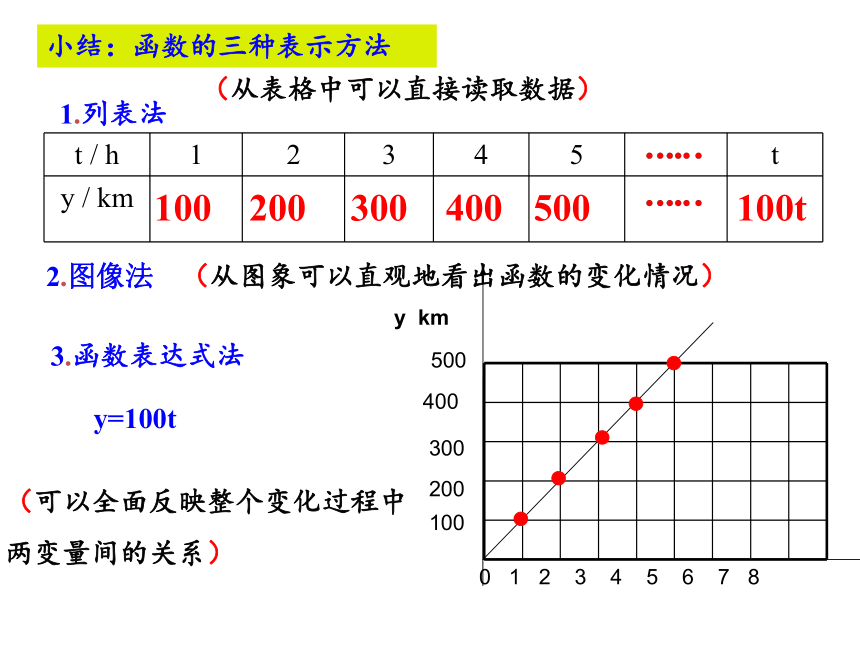
1.列表法
t / h 1 2 3 4 5 t
y / km
100
200
300
400
500
100t
2.图像法
3.函数表达式法
y=100t
小结:函数的三种表示方法
(从表格中可以直接读取数据)
(从图象可以直观地看出函数的变化情况)
(可以全面反映整个变化过程中
两变量间的关系)
0 1 2 3 4 5 6 7 8
500
400
300
200
100
t h
y km
汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q (L)与行驶路程 s (km) 的函数表达式.
(2)你知道汽车行驶50km、100km、200km时,油箱中剩余油量分别是多少吗?
(3)你认为这辆汽车现有油量够它行驶多远?
(4)s的值最小取___,s的取值范围是___
注意:在实际问题中,自变量的取值通常有一定的范围.
0≤s≤400
0
1.商店有100支铅笔.
(1)如果卖出x支,还剩y 支,那么y = ;
(2)当x越来越大时,y会发生什么变化?
(3)请写出自变量取值范围.
________________________
y随x增大而减小.
0≤x≤100,且x为整数.
100-x
注意:在实际问题中,确定函数中自变量取值范围时,必须使实际问题有意义.
试一试
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐,涨落的水位称为潮位.如图是我国某港某天的实时潮位图.
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象.
在图中,潮位仪绘制的平滑曲线,揭示了潮位y(m)与时间t(h)之间的函数关系.
在图中你读到 了哪些信息
图形会说话
小明骑自行车从甲地到乙地,图中的折线表示小明的行程 s (km)与途中所花时间 t (h)之间的函数关系.
(1)小明从甲地到乙地用了多少时间?
(2)小明出发5h时距离甲地有多远?请说明图中点p表示的实际意义;
(3)折线中有一条平
行于t轴的线段,它的
意义是什么?
(4)你还能从图中获得哪些信息?请与同伴交流.
1.某游客为爬上3千米高的山顶看日出。先用1小时爬了2千米,休息0.5小时后,用1小时爬上山顶。游客爬山所用时间t与山高h间的函数关系用图形表示是( )
C
试一试
A
B
C
D
2. 甲、乙两人出去散步,用20 min走了900 m后,甲随即按原速返回.乙遇到一位朋友,并与朋友交谈了10min后,用15min时间回到家里.下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?哪一个表示乙离家的路程与时间之间的函数关系?
(1)
s
t
O
50
40
30
20
10
900
100
(2)
s
t
O
50
40
30
20
10
900
100
(3)
s
t
O
50
40
30
20
10
900
100
(4)
s
t
O
50
40
30
20
10
900
100
甲
乙
3.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km; b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;d.甲乙两人途中没有相遇过.
根据图象信息,以上说法正确的是 ( )
B
s/km
t/h
B、2个
D、4个
C、3个
甲
乙
A、 1个
课堂检测(6 7题自选)
1.在函数关系式y=-x+2中,当x=-3时,y= __ 当y=0时
x= ____
2.在函数y= 中,自变量x的取值范围____. .
3.弹簧挂上物体后会伸长,在一定范围内测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有如下关系:
请写出弹簧总长y(cm)与所挂物体质量x(kg)之间的函数
关系式y=______ (2)当挂重10千克时弹簧的总长是____
x / kg 0 1 2 3 4 5 6
y /c m 12 12.5 13 13.5 14 14.5 15
5
2
x≠2
4.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是y=________,自变量的取值范围__________度
180-2x
0<x<90
12+0.5x
17c m
5.如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B—C-D作匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图像大致是( ).
B
课堂检测
6.如图:每个图形都是由若干棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个图案的棋子总数为S。
s与n之间能用函数关系式表示吗?自变量的取值范围是什么
S与 n的函数关系式:S=4n -4
n的取值范围:n>1的整数
n 2 3 4 5 …
s 4 8 12 16 …
课堂检测
⑴甲出发几小时,乙才开始出发?
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
7.如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
课堂检测
1.如图所示,在矩形ABCD中,动点P从点B出发,沿BC, CD, DA运动到A处停止,设点P运动的路程为x,ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积为 。
动画
拓展提高
10
我有哪些收获呢?
与大家共分享!
1.表示两个变量间的关系的方法.
2.能根据实际问题的意义以及函数关系式,确定函数
的自变量取值范围,并会求出函数值.
3.从图象中获得信息并能用语言合理的表示,并能结
合具体的情境理解图象上的点所表示的数学意义.
这节课你有哪些收获
4.重要数学思想与方法:数形结合 、建模、函数.
作业
A(必做题)书 P141 2-4题
B(选做题)学案看图说故事题
看图说故事.
请你编写一个故事,使故事情境中出现的一对
变量x,y满足图示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据和变化规律提出一个问题,并解答这个问题.
敬 请 指 正
谢 谢
6.1 函数
如果在一个变化过程中,有两个变量,如x和y,对于x的每一个值,y都有唯一的值与之对应,那么我们称y是x的___.其中x是_____.
在某一变化过程中,可以取不同数值的量,叫做_____.还有一种量,它的取值始终保持不变,称之为____.
你还记得吗
变量
常量
自变量
函数
七点 八点 九点
100KM
200KM
情境导入:
小丽乘汽车去旅游.汽车在公路上匀速行驶。
汽车以100km/h的速度匀速行驶,在这一变化过程中,
(1)有哪些变量?哪些常量?
(2)变量之间是函数关系吗?为什么?
(3)若汽车行驶的时间为t(h),汽车行驶的路程为y(km).怎样表示函数y与自变量t的关系?
1.可以列表表示:
t / h 1 2 3 4 5 t
y / km
100
200
300
400
500
100t
在汽车以100km/h的速度匀速行驶,这一变化过程中:
把自变量t的一系列值和函数y的对应值列成一个表,这种表示函数关系的方法是列表法.
在汽车以100km/h的速度匀速行驶,这一变化过程中:
t/h 1 2 3 4 …
y/km 100 200 300 400 …
在直角坐标系中,以函数的自变量的值为横坐标、相应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
2.可以在直角坐标系中画图表示:
像y=100t 、S=6n+2等表示两个变量之间关系的式子称为函数表达式.
3.可以列式表示:
y=100t
1.列表法
t / h 1 2 3 4 5 t
y / km
100
200
300
400
500
100t
2.图像法
3.函数表达式法
y=100t
小结:函数的三种表示方法
(从表格中可以直接读取数据)
(从图象可以直观地看出函数的变化情况)
(可以全面反映整个变化过程中
两变量间的关系)
0 1 2 3 4 5 6 7 8
500
400
300
200
100
t h
y km
汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q (L)与行驶路程 s (km) 的函数表达式.
(2)你知道汽车行驶50km、100km、200km时,油箱中剩余油量分别是多少吗?
(3)你认为这辆汽车现有油量够它行驶多远?
(4)s的值最小取___,s的取值范围是___
注意:在实际问题中,自变量的取值通常有一定的范围.
0≤s≤400
0
1.商店有100支铅笔.
(1)如果卖出x支,还剩y 支,那么y = ;
(2)当x越来越大时,y会发生什么变化?
(3)请写出自变量取值范围.
________________________
y随x增大而减小.
0≤x≤100,且x为整数.
100-x
注意:在实际问题中,确定函数中自变量取值范围时,必须使实际问题有意义.
试一试
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐,涨落的水位称为潮位.如图是我国某港某天的实时潮位图.
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象.
在图中,潮位仪绘制的平滑曲线,揭示了潮位y(m)与时间t(h)之间的函数关系.
在图中你读到 了哪些信息
图形会说话
小明骑自行车从甲地到乙地,图中的折线表示小明的行程 s (km)与途中所花时间 t (h)之间的函数关系.
(1)小明从甲地到乙地用了多少时间?
(2)小明出发5h时距离甲地有多远?请说明图中点p表示的实际意义;
(3)折线中有一条平
行于t轴的线段,它的
意义是什么?
(4)你还能从图中获得哪些信息?请与同伴交流.
1.某游客为爬上3千米高的山顶看日出。先用1小时爬了2千米,休息0.5小时后,用1小时爬上山顶。游客爬山所用时间t与山高h间的函数关系用图形表示是( )
C
试一试
A
B
C
D
2. 甲、乙两人出去散步,用20 min走了900 m后,甲随即按原速返回.乙遇到一位朋友,并与朋友交谈了10min后,用15min时间回到家里.下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?哪一个表示乙离家的路程与时间之间的函数关系?
(1)
s
t
O
50
40
30
20
10
900
100
(2)
s
t
O
50
40
30
20
10
900
100
(3)
s
t
O
50
40
30
20
10
900
100
(4)
s
t
O
50
40
30
20
10
900
100
甲
乙
3.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km; b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;d.甲乙两人途中没有相遇过.
根据图象信息,以上说法正确的是 ( )
B
s/km
t/h
B、2个
D、4个
C、3个
甲
乙
A、 1个
课堂检测(6 7题自选)
1.在函数关系式y=-x+2中,当x=-3时,y= __ 当y=0时
x= ____
2.在函数y= 中,自变量x的取值范围____. .
3.弹簧挂上物体后会伸长,在一定范围内测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有如下关系:
请写出弹簧总长y(cm)与所挂物体质量x(kg)之间的函数
关系式y=______ (2)当挂重10千克时弹簧的总长是____
x / kg 0 1 2 3 4 5 6
y /c m 12 12.5 13 13.5 14 14.5 15
5
2
x≠2
4.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是y=________,自变量的取值范围__________度
180-2x
0<x<90
12+0.5x
17c m
5.如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B—C-D作匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图像大致是( ).
B
课堂检测
6.如图:每个图形都是由若干棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个图案的棋子总数为S。
s与n之间能用函数关系式表示吗?自变量的取值范围是什么
S与 n的函数关系式:S=4n -4
n的取值范围:n>1的整数
n 2 3 4 5 …
s 4 8 12 16 …
课堂检测
⑴甲出发几小时,乙才开始出发?
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
7.如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
课堂检测
1.如图所示,在矩形ABCD中,动点P从点B出发,沿BC, CD, DA运动到A处停止,设点P运动的路程为x,ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积为 。
动画
拓展提高
10
我有哪些收获呢?
与大家共分享!
1.表示两个变量间的关系的方法.
2.能根据实际问题的意义以及函数关系式,确定函数
的自变量取值范围,并会求出函数值.
3.从图象中获得信息并能用语言合理的表示,并能结
合具体的情境理解图象上的点所表示的数学意义.
这节课你有哪些收获
4.重要数学思想与方法:数形结合 、建模、函数.
作业
A(必做题)书 P141 2-4题
B(选做题)学案看图说故事题
看图说故事.
请你编写一个故事,使故事情境中出现的一对
变量x,y满足图示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据和变化规律提出一个问题,并解答这个问题.
敬 请 指 正
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
