2021-2022学年苏科版八年级数学上册3.3 勾股定理的简单应用 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册3.3 勾股定理的简单应用 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 838.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 17:11:50 | ||
图片预览






文档简介
(共21张PPT)
2021
3.3 勾股定理的简单应用
八年级上册
复习回顾
1
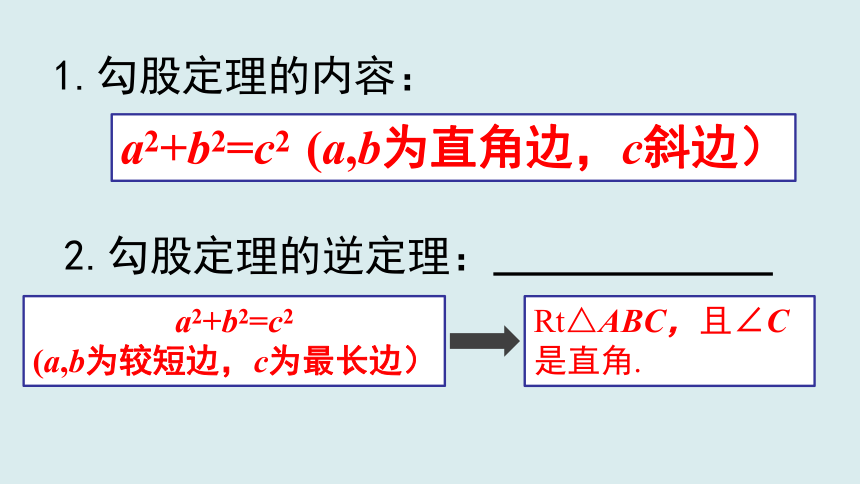
1.勾股定理的内容:
2.勾股定理的逆定理:
a2+b2=c2 (a,b为直角边,c斜边)
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
1.已知一个直角三角形的两边长分别为3和5,则第三边长的平方为( )
A.16 B.16或56 C.16或34 D.4或34
C
2.若三角形的三边长a、b、c满足(a+b)2=c2+2ab,则这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
3.以下列各组线段a、b、c为边的三角形中,不是直角三角形的是( )
A.a=1.5, b=2, c=3 B.a=7, b=24, c=25
C.a=6, b=8, c=10 D.a=3, b=4, c=5
A
教学新知
2
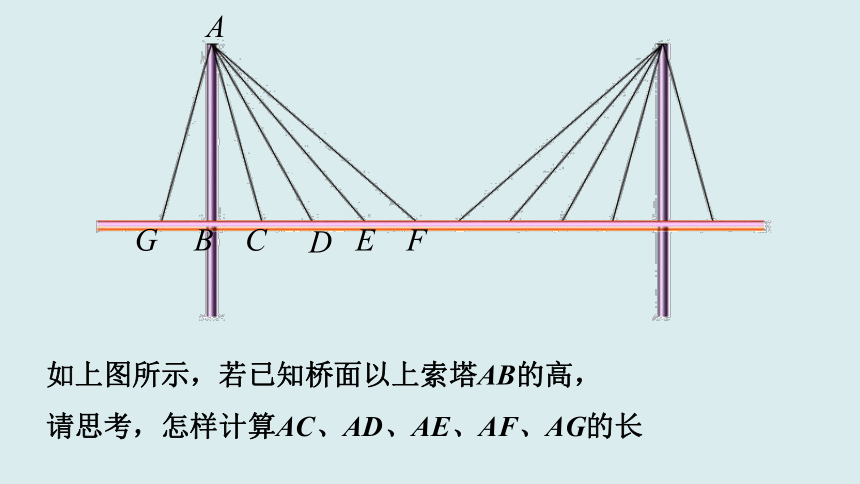
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
A
B
C
E
F
G
D
如上图所示,若已知桥面以上索塔AB的高,
请思考,怎样计算AC、AD、AE、AF、AG的长
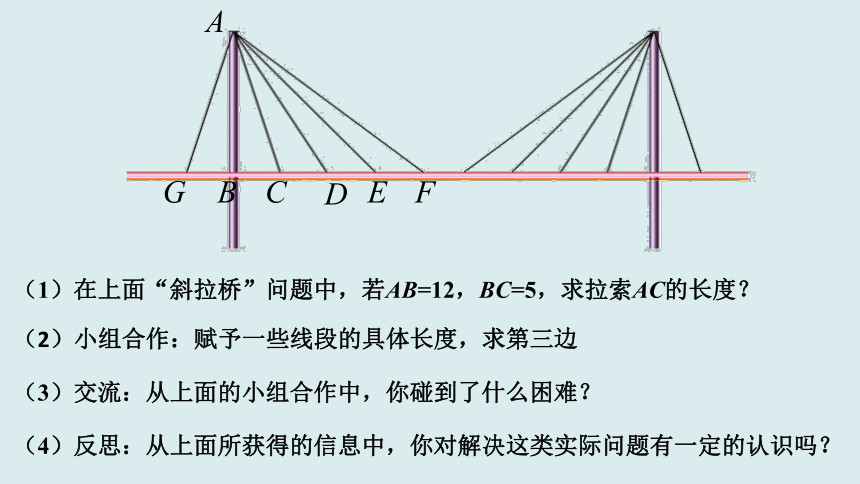
(1)在上面“斜拉桥”问题中,若AB=12,BC=5,求拉索AC的长度?
(2)小组合作:赋予一些线段的具体长度,求第三边
(3)交流:从上面的小组合作中,你碰到了什么困难?
(4)反思:从上面所获得的信息中,你对解决这类实际问题有一定的认识吗?
A
B
C
E
F
G
D
例1:《九章算术》中的“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
解析:方程思想是解决数学问题常用的重要思想
若设折断处离地面高度为 x 尺,则竹子折断处到竹梢的长度应为 尺(用含x的代数式表示)
解:如图,我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,用线段OB来表示竹梢触地处离竹根的距离.设OA= x,则 AB=10- x.
由勾股定理得 x2 + 32 =(10-x)2.
解得 x = 4.55,
∴折断处离地面 4.55 尺.
A
O
B
x
(10-x)
3
例2:如图,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,
求AC.
解:∵AD是BC边上的中线,且BC=20,
D
C
B
A
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴ AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
课堂练习
3
1.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里
B.30海里
C.40海里
D.50海里
C
2.如图,校园内有两棵树,一棵树高13 m,另一棵树高8 m,两树相距12 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.10 m
B.11 m
C.12 m
D.13 m
D
3.如图,已知CD=6cm,AD=8cm, ∠ADC=90°,BC=24cm,AB=26cm,
求阴影部分面积.
A
B
C
D
解:在Rt△ADC中,
∵AC2 = AD2 + CD2(勾股定理)
= 82 + 62 = 100,
∴AC = 10.
∵AC2 + BC2 = 102 + 242 = 676 = 262,
∴△ACB为直角三角形(勾股定理的逆定理)
∴S阴影部分 = S△ACB - S△ACD
=120 - 24
= 96.
课堂小结
4
知识点一 勾股定理的应用
勾股定理的运用类型:
(1)在直角三角形中,知道两边长可求第三边长;
(2)在直角三角形中,知道一边长和另两边长的关系,可求另两边长.
知识点二 勾股定理的逆定理的应用
已知三角形的三边长时,可以利用勾股定理的逆定理判断该三角形是不是直角三角形,若两条较短边的平方和等于第三边的平方,则第三边所对的角是直角.
拓展提升
5
1、如图,在△ABC中,AB=15,BC=14,AC=13, 求△ABC的面积。
∵ AD⊥BC ∴ ∠ADB =∠ADC = 90°
∴AD2 = AB2 - BD2 AD2 = AC2 - CD2
D
∴ AB2 - BD2 = AC2 - CD2
13
∴ 152 - x2 = 132 – (14 - x) 2
∴ x=9 ∴BD=9
∴AD2 = AB2 - BD2 =144
∴ AD=12(负数舍去)
∴ △ABC的面积 = BC×AD÷2 = 84
解:作AD⊥BC ,垂足为 D
设 BD = x,则 CD = 14-x
B
C
15
14
A
2.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.
解:如图,
BC为芦苇长,AB为水深,AC为池中心点距岸边的距离.
设 AB = x尺,
则 BC =( x +1)尺,
根据勾股定理得:
x2+52 = (x+1)2,
即(x+1)2-x2 = 52,
解得:x = 12,
所以芦苇长为 12+1 = 13(尺),
答:水深为12尺,芦苇长为13尺.
A
C
B
2021
3.3 勾股定理的简单应用
八年级上册
复习回顾
1
1.勾股定理的内容:
2.勾股定理的逆定理:
a2+b2=c2 (a,b为直角边,c斜边)
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
1.已知一个直角三角形的两边长分别为3和5,则第三边长的平方为( )
A.16 B.16或56 C.16或34 D.4或34
C
2.若三角形的三边长a、b、c满足(a+b)2=c2+2ab,则这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
3.以下列各组线段a、b、c为边的三角形中,不是直角三角形的是( )
A.a=1.5, b=2, c=3 B.a=7, b=24, c=25
C.a=6, b=8, c=10 D.a=3, b=4, c=5
A
教学新知
2
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
A
B
C
E
F
G
D
如上图所示,若已知桥面以上索塔AB的高,
请思考,怎样计算AC、AD、AE、AF、AG的长
(1)在上面“斜拉桥”问题中,若AB=12,BC=5,求拉索AC的长度?
(2)小组合作:赋予一些线段的具体长度,求第三边
(3)交流:从上面的小组合作中,你碰到了什么困难?
(4)反思:从上面所获得的信息中,你对解决这类实际问题有一定的认识吗?
A
B
C
E
F
G
D
例1:《九章算术》中的“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
解析:方程思想是解决数学问题常用的重要思想
若设折断处离地面高度为 x 尺,则竹子折断处到竹梢的长度应为 尺(用含x的代数式表示)
解:如图,我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,用线段OB来表示竹梢触地处离竹根的距离.设OA= x,则 AB=10- x.
由勾股定理得 x2 + 32 =(10-x)2.
解得 x = 4.55,
∴折断处离地面 4.55 尺.
A
O
B
x
(10-x)
3
例2:如图,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,
求AC.
解:∵AD是BC边上的中线,且BC=20,
D
C
B
A
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴ AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
课堂练习
3
1.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里
B.30海里
C.40海里
D.50海里
C
2.如图,校园内有两棵树,一棵树高13 m,另一棵树高8 m,两树相距12 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.10 m
B.11 m
C.12 m
D.13 m
D
3.如图,已知CD=6cm,AD=8cm, ∠ADC=90°,BC=24cm,AB=26cm,
求阴影部分面积.
A
B
C
D
解:在Rt△ADC中,
∵AC2 = AD2 + CD2(勾股定理)
= 82 + 62 = 100,
∴AC = 10.
∵AC2 + BC2 = 102 + 242 = 676 = 262,
∴△ACB为直角三角形(勾股定理的逆定理)
∴S阴影部分 = S△ACB - S△ACD
=120 - 24
= 96.
课堂小结
4
知识点一 勾股定理的应用
勾股定理的运用类型:
(1)在直角三角形中,知道两边长可求第三边长;
(2)在直角三角形中,知道一边长和另两边长的关系,可求另两边长.
知识点二 勾股定理的逆定理的应用
已知三角形的三边长时,可以利用勾股定理的逆定理判断该三角形是不是直角三角形,若两条较短边的平方和等于第三边的平方,则第三边所对的角是直角.
拓展提升
5
1、如图,在△ABC中,AB=15,BC=14,AC=13, 求△ABC的面积。
∵ AD⊥BC ∴ ∠ADB =∠ADC = 90°
∴AD2 = AB2 - BD2 AD2 = AC2 - CD2
D
∴ AB2 - BD2 = AC2 - CD2
13
∴ 152 - x2 = 132 – (14 - x) 2
∴ x=9 ∴BD=9
∴AD2 = AB2 - BD2 =144
∴ AD=12(负数舍去)
∴ △ABC的面积 = BC×AD÷2 = 84
解:作AD⊥BC ,垂足为 D
设 BD = x,则 CD = 14-x
B
C
15
14
A
2.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.
解:如图,
BC为芦苇长,AB为水深,AC为池中心点距岸边的距离.
设 AB = x尺,
则 BC =( x +1)尺,
根据勾股定理得:
x2+52 = (x+1)2,
即(x+1)2-x2 = 52,
解得:x = 12,
所以芦苇长为 12+1 = 13(尺),
答:水深为12尺,芦苇长为13尺.
A
C
B
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
