3.4一元一次方程模型的应用--行程问题 湘教版初中数学七年级上册 课件(共21张PPT)
文档属性
| 名称 | 3.4一元一次方程模型的应用--行程问题 湘教版初中数学七年级上册 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 672.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
行程问题
3.4一元一次方程模型的应用
总量=部分之和
路程=速度×时间
二、追及问题
一、相遇问题
一、课前热身
2、常见的行程问题:
1、相关公式:
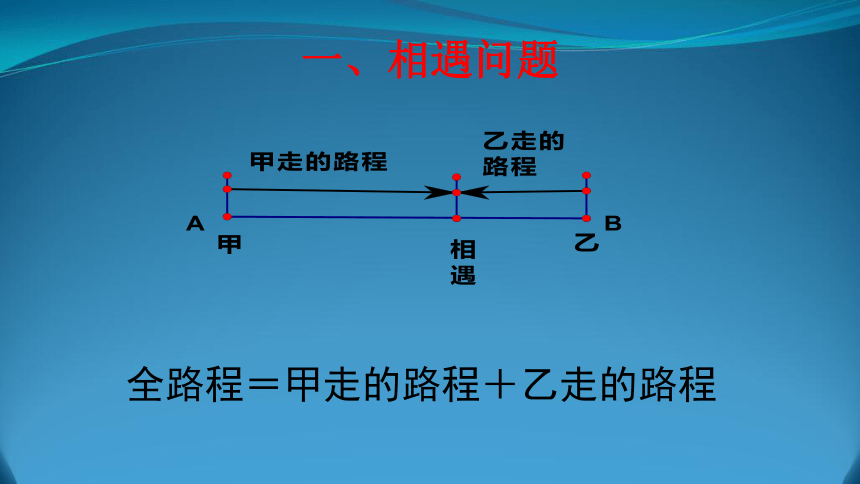
一、相遇问题
全路程=甲走的路程+乙走的路程
讲授新课
相遇问题
情景引入
老师和同学在相距2米的地方,他们同时出发,相向而行,他们能相遇吗?
等量关系:
老师走的路程+同学走的路程=相距的路程
所用公式:路程=速度×时间
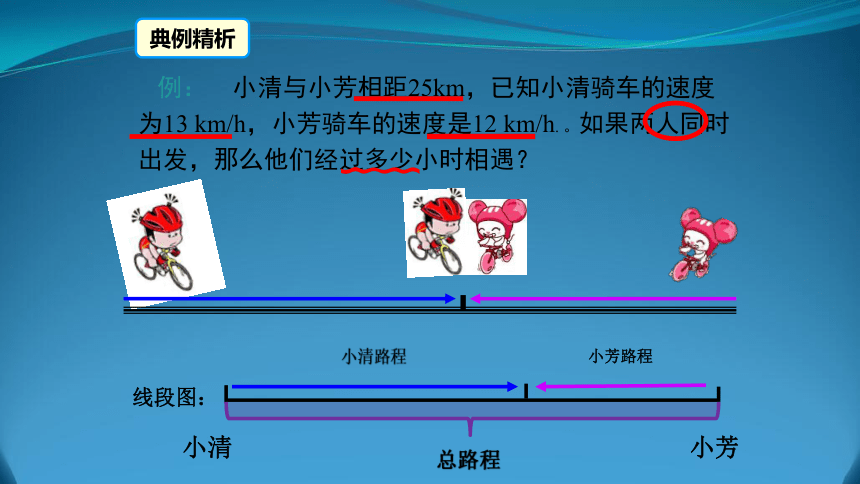
例: 小清与小芳相距25km,已知小清骑车的速度为13 km/h,小芳骑车的速度是12 km/h. 。如果两人同时出发,那么他们经过多少小时相遇?
典例精析
﹏
小清路程
小芳路程
线段图:
总路程
小清
小芳
两人从两地出发相向而行的行程问题称为相遇问题.
甲路程+乙路程=总路程.
归纳总结
行程问题,借助“线段图”分析数量关系.
甲路程
乙路程
1、同时不同地:
甲为快者,乙为慢者,则有:
a:甲走路程=乙走路程+被追路程
b:甲所用时间=乙所用时间
二、追及问题
2、同地不同时:
甲为快者,乙为慢者,则有:
a:甲走路程=乙走路程
b:乙所用时间=甲所用时间+多用时间
追及问题
例: 小清与小芳家相距40米,小清在小芳后面,小清每分钟骑80米,小芳每分钟骑60米,两人同时从家出发骑自行车上学,问小清几分钟追上小芳?
40米
情景引入
(1)同时不同地的问题,如图所示,
甲路程=乙路程+相距路程;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
归纳总结
乙路程
甲路程
例:放学后骑车回家,小明以80米/分钟的速度出发,5分钟后,小红发现 他忘了带书包,于是,小红立即以180米/分钟的速度去追小明.追上小明用了多长时间?
追及问题
典例精析
分析:当小红追上小明时,两人所走路程相等.
解:(1)设小红追上小明用了x分钟.
据题意,得 80×5+80x=180x.
答:小红追上小明用了4分钟.
解得 x=4.
80×5
80x
180x
(2)对于同地不同时的追及问题,如图所示,
甲路程=乙路程.
甲路程
甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时。
(1)甲、乙二人经过多长时间相遇
(2)甲、乙二人经过多长时间第一次相距32千米
(4)若将此题中的相向而行改为背向而行,还会相遇吗
会出现什么情况 他们何时相距240千米?
二、例题 分析:
(3)如果甲先1 小时,乙才出发,问甲一共走多长时间
与乙相遇
(1)
(2)
(3)
(4)
(5)
例题 .甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
分析:先看单位是否统一,
题目直接描述,是相遇问题,
路程 = 速度和 × 时间
144 = (6+10) × ?
?
(1)解:设甲、乙二人经过x小时相遇,据题意,得
144= (6+10) x
16x=144
x=9.
答:甲乙二人经过9小时相遇.
(1)甲、乙二人经过多长时间相遇
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
32km
(2)甲、乙二人经过多长时间第一次相距32千米
分析:甲、乙二人经过多长时间第一次相距32千米
路程 = 速度和 × 时间
144-32 = (6+10) × ?
解:设甲、乙二人经过x小时第一次相距32千米,
据题意,得
144-32= (6+10) x
112=16x
x=7.
答:甲乙二人经过7小时第一次相距32千米.
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
(3)如果甲先1 小时,乙才出发,问甲一共走多长时间
与乙相遇
分析:
甲先走 小时,
乙才出发,问甲一共走多长时间
与乙相遇
144 = 甲路程 + 乙路程
144 = 6x + 10(x- )
解:设甲一共走x小时与乙相遇,则乙此时走了(x - )
小时后相遇,列方程,得
144 =6x + 10(x- )
答:乙出发 小时,与甲相遇.
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
?
240千米
分析:背向而行,不会相遇.
(4)若将此题中的相向而行改为背向而行,还会相遇吗
会出现什么情况 他们何时相距240千米?
何时相距240千米
路程 = 速度和 × 时间
240-144 = (10+6 ) × ?
解:设甲、乙二人经过x小时相距240千米,据题意,得
240-144 =(10+6)x
16x=96
x=6.
答:两人背向而行,经过6小时,相距240千米.
10
6
A
B
甲
乙
三、巩固提升:
A、B两地相距100km,甲、乙两人骑自行车分别从A、B两地出发相向而行,甲的速度是23km/h,乙的速度是21km/h,甲骑了1h后,乙从B地出发,问甲经过多少时间与乙相遇?
甲的路程+乙的路程=总路程
甲路程=乙路程+相距路程
追及问题
相遇问题
四、课堂小结
这节课你们有哪些收获?
甲路程=乙路程
同时不同地
同地不同时
五、课堂检测:
1. A,B两地相距44千米,甲每小时行5千米,乙的速度是甲的1.2倍,如果甲,乙分别从A、B两地同时出发相向而行,那么经过______小时两人相遇.
2.已知A、B两地相距60千米,甲、乙两人分别从A、B两地相向而行,甲的速度是20千米/时,乙的速度是30千米/时,求何时两人相距10千米?
行程问题
3.4一元一次方程模型的应用
总量=部分之和
路程=速度×时间
二、追及问题
一、相遇问题
一、课前热身
2、常见的行程问题:
1、相关公式:
一、相遇问题
全路程=甲走的路程+乙走的路程
讲授新课
相遇问题
情景引入
老师和同学在相距2米的地方,他们同时出发,相向而行,他们能相遇吗?
等量关系:
老师走的路程+同学走的路程=相距的路程
所用公式:路程=速度×时间
例: 小清与小芳相距25km,已知小清骑车的速度为13 km/h,小芳骑车的速度是12 km/h. 。如果两人同时出发,那么他们经过多少小时相遇?
典例精析
﹏
小清路程
小芳路程
线段图:
总路程
小清
小芳
两人从两地出发相向而行的行程问题称为相遇问题.
甲路程+乙路程=总路程.
归纳总结
行程问题,借助“线段图”分析数量关系.
甲路程
乙路程
1、同时不同地:
甲为快者,乙为慢者,则有:
a:甲走路程=乙走路程+被追路程
b:甲所用时间=乙所用时间
二、追及问题
2、同地不同时:
甲为快者,乙为慢者,则有:
a:甲走路程=乙走路程
b:乙所用时间=甲所用时间+多用时间
追及问题
例: 小清与小芳家相距40米,小清在小芳后面,小清每分钟骑80米,小芳每分钟骑60米,两人同时从家出发骑自行车上学,问小清几分钟追上小芳?
40米
情景引入
(1)同时不同地的问题,如图所示,
甲路程=乙路程+相距路程;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
归纳总结
乙路程
甲路程
例:放学后骑车回家,小明以80米/分钟的速度出发,5分钟后,小红发现 他忘了带书包,于是,小红立即以180米/分钟的速度去追小明.追上小明用了多长时间?
追及问题
典例精析
分析:当小红追上小明时,两人所走路程相等.
解:(1)设小红追上小明用了x分钟.
据题意,得 80×5+80x=180x.
答:小红追上小明用了4分钟.
解得 x=4.
80×5
80x
180x
(2)对于同地不同时的追及问题,如图所示,
甲路程=乙路程.
甲路程
甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时。
(1)甲、乙二人经过多长时间相遇
(2)甲、乙二人经过多长时间第一次相距32千米
(4)若将此题中的相向而行改为背向而行,还会相遇吗
会出现什么情况 他们何时相距240千米?
二、例题 分析:
(3)如果甲先1 小时,乙才出发,问甲一共走多长时间
与乙相遇
(1)
(2)
(3)
(4)
(5)
例题 .甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
分析:先看单位是否统一,
题目直接描述,是相遇问题,
路程 = 速度和 × 时间
144 = (6+10) × ?
?
(1)解:设甲、乙二人经过x小时相遇,据题意,得
144= (6+10) x
16x=144
x=9.
答:甲乙二人经过9小时相遇.
(1)甲、乙二人经过多长时间相遇
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
32km
(2)甲、乙二人经过多长时间第一次相距32千米
分析:甲、乙二人经过多长时间第一次相距32千米
路程 = 速度和 × 时间
144-32 = (6+10) × ?
解:设甲、乙二人经过x小时第一次相距32千米,
据题意,得
144-32= (6+10) x
112=16x
x=7.
答:甲乙二人经过7小时第一次相距32千米.
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
(3)如果甲先1 小时,乙才出发,问甲一共走多长时间
与乙相遇
分析:
甲先走 小时,
乙才出发,问甲一共走多长时间
与乙相遇
144 = 甲路程 + 乙路程
144 = 6x + 10(x- )
解:设甲一共走x小时与乙相遇,则乙此时走了(x - )
小时后相遇,列方程,得
144 =6x + 10(x- )
答:乙出发 小时,与甲相遇.
10
6
A
B
甲
乙
例题.甲、乙二人分别从相距144千米的A、B两地同时出发相向而行,甲的速度是6千米/时,乙的速度是10千米/时,
144千米
?
240千米
分析:背向而行,不会相遇.
(4)若将此题中的相向而行改为背向而行,还会相遇吗
会出现什么情况 他们何时相距240千米?
何时相距240千米
路程 = 速度和 × 时间
240-144 = (10+6 ) × ?
解:设甲、乙二人经过x小时相距240千米,据题意,得
240-144 =(10+6)x
16x=96
x=6.
答:两人背向而行,经过6小时,相距240千米.
10
6
A
B
甲
乙
三、巩固提升:
A、B两地相距100km,甲、乙两人骑自行车分别从A、B两地出发相向而行,甲的速度是23km/h,乙的速度是21km/h,甲骑了1h后,乙从B地出发,问甲经过多少时间与乙相遇?
甲的路程+乙的路程=总路程
甲路程=乙路程+相距路程
追及问题
相遇问题
四、课堂小结
这节课你们有哪些收获?
甲路程=乙路程
同时不同地
同地不同时
五、课堂检测:
1. A,B两地相距44千米,甲每小时行5千米,乙的速度是甲的1.2倍,如果甲,乙分别从A、B两地同时出发相向而行,那么经过______小时两人相遇.
2.已知A、B两地相距60千米,甲、乙两人分别从A、B两地相向而行,甲的速度是20千米/时,乙的速度是30千米/时,求何时两人相距10千米?
同课章节目录
