3.2.2双曲线的简单几何性质(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(知识梳理+例题+变式+练习)(解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 742.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
3.2.2双曲线的简单几何性质
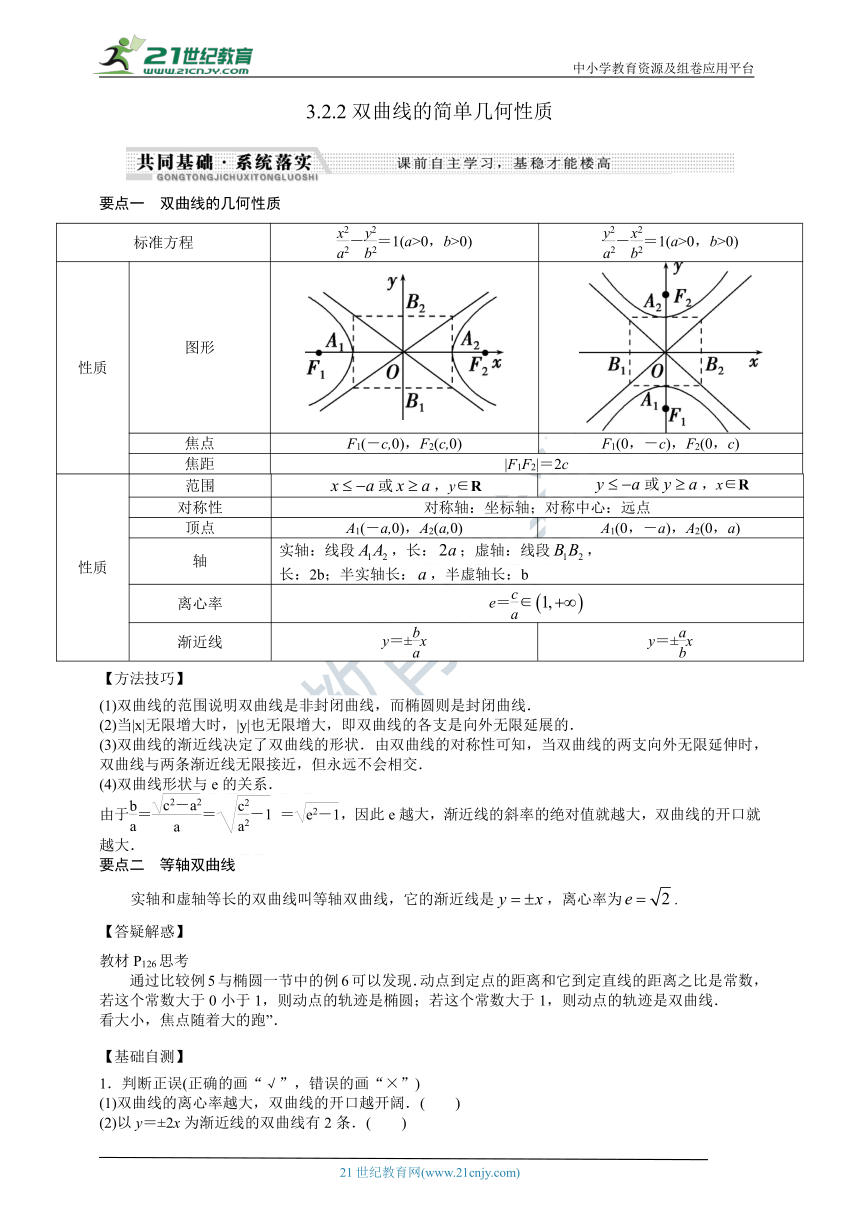
要点一 双曲线的几何性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
性质 图形
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
性质 范围 或,y∈R 或,x∈R
对称性 对称轴:坐标轴;对称中心:远点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段,长:;虚轴:线段,长:2b;半实轴长:,半虚轴长:b
离心率 e=∈
渐近线 y=±x y=±x
【方法技巧】
(1)双曲线的范围说明双曲线是非封闭曲线,而椭圆则是封闭曲线.
(2)当|x|无限增大时,|y|也无限增大,即双曲线的各支是向外无限延展的.
(3)双曲线的渐近线决定了双曲线的形状.由双曲线的对称性可知,当双曲线的两支向外无限延伸时,双曲线与两条渐近线无限接近,但永远不会相交.
(4)双曲线形状与e的关系.
由于== =,因此e越大,渐近线的斜率的绝对值就越大,双曲线的开口就越大.
要点二 等轴双曲线
实轴和虚轴等长的双曲线叫等轴双曲线,它的渐近线是,离心率为.
【答疑解惑】
教材P126思考
通过比较例5与椭圆一节中的例6可以发现.动点到定点的距离和它到定直线的距离之比是常数,若这个常数大于0小于1,则动点的轨迹是椭圆;若这个常数大于1,则动点的轨迹是双曲线.
看大小,焦点随着大的跑”.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)双曲线的离心率越大,双曲线的开口越开阔.( )
(2)以y=±2x为渐近线的双曲线有2条.( )
(3)方程-=1(a>0,b>0)的渐近线方程为y=±x.( )
(4)离心率e越大,双曲线-=1的渐近线的斜率绝对值越大.( )
【答案】(1)√(2)×(3)×(4)×
2.实轴长为2,虚轴长为4的双曲线的标准方程是( )
A.x2-=1
B.y2-=1
C.-=1或-=1
D.x2-=1或y2-=1
【答案】D
【解析】由题意知2a=2,2b=4∴a=1,b=2,∴a2=1,b2=4又双曲线的焦点位置不确定,故选D.
3.双曲线-y2=1的渐近线方程是( )
A.y=±x B.y=±x C.y=±2x D.y=±x
【答案】B
【解析】由双曲线方程得:a=,b=1,∴渐近线方程为:y=±x=±x.故选B.
4.若双曲线-=1(a>0,b>0)的两条渐近线互相垂直,则该双曲线的离心率是________.
【答案】
【解析】由题意知渐近线与x轴的夹角θ=∴=tan=1∴e==
题型一 由双曲线的几何性质求其标准方程
1.已知双曲线-=1(a>0,b>0)的右焦点为F,点A在双曲线的渐近线上,△OAF是边长为2的等边三角形(O为原点),则双曲线的方程为( )
A.-=1 B.-=1 C.-y2=1 D.x2-=1
【答案】D
【解析】不妨设点A在第一象限,由题意可知c=2,点A的坐标为(1,),所以=,又c2=a2+b2,所以a2=1,b2=3,故所求双曲线的方程为x2-=1,故选D.
2.焦点为(0,6),且与双曲线-y2=1有相同的渐近线的双曲线方程是________.
【答案】-=1
【解析】由-y2=1,得双曲线的渐近线为y=±x.设双曲线方程为:-y2=λ(λ<0),∴-=1,∴-λ-2λ=36,∴λ=-12.
故双曲线方程为-=1.
3.过点(2,0),与双曲线-=1离心率相等的双曲线方程为________.
【答案】-y2=1
【解析】当所求双曲线的焦点在x轴上时,可设其方程为-=λ(λ>0),将点(2,0)的坐标代入方程得λ=,故所求双曲线的标准方程为-y2=1;
当所求双曲线的焦点在y轴上时,可设其方程为-=λ(λ>0),将点(2,0)的坐标代入方程得λ=-<0(舍去).综上可知,所求双曲线的标准方程为-y2=1.
4.与椭圆+=1有公共焦点,离心率为的双曲线方程为________.
【答案】-=1
【解析】方法一 由椭圆方程可得焦点坐标为(-3,0),(3,0),即c=3且焦点在x轴上.
设双曲线的标准方程为-=1(a>0,b>0).
因为e==,所以a=2,则b2=c2-a2=5,故所求双曲线的标准方程为-=1.
方法二 因为椭圆焦点在x轴上,所以可设双曲线的标准方程为-=1(16<λ<25).
因为e=,所以=-1,解得λ=21.故所求双曲线的标准方程为-=1.
【方法技巧】
由几何性质求双曲线标准方程的解题思路
1.由双曲线的几何性质求双曲线的标准方程,一般用待定系数法.当双曲线的焦点不明确时,方程可能有两种形式,此时应注意分类讨论,为了避免讨论,也可设双曲线的方程为mx2-ny2=1(mn>0).
2.常见双曲线方程的设法
(1)渐近线为y=±x的双曲线方程可设为-=λ(λ≠0,m>0,n>0);如果两条渐近线的方程为Ax±By=0,那么双曲线的方程可设为A2x2-B2y2=m(m≠0,A>0,B>0).
(2)与双曲线-=1或-=1(a>0,b>0)共渐近线的双曲线方程可设为-=λ或-=λ(λ≠0).
(3)与双曲线-=1(a>0,b>0)离心率相等的双曲线系方程可设为-=λ(λ>0)或-=λ(λ>0),这是因为由离心率不能确定焦点位置.
(4)与椭圆+=1(a>b>0)共焦点的双曲线系方程可设为-=1(b2<λ题型二 与椭圆有关的轨迹问题
探究1 利用方程求解几何性质
【例1】(多选)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-5,0),F2(5,0),则能使双曲线C的方程为-=1的是( )
A.离心率为 B.双曲线过点(5,)
C.渐近线方程为3x±4y=0 D.实轴长为4
【答案】ABC
【解析】双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-5,0),F2(5,0).
可得c=5,如果离心率为:.可得a=4,则b=3,所以,双曲线C的方程为-=1,所以A正确;
c=5,双曲线过点,可得解得a=4,b=3,所以双曲线C的方程为-=1,所以B正确;
c=5,渐近线方程为3x±4y=0,可得=,a2+b2=25,
解得a=4,b=3,所以双曲线C的方程为-=1,所以C正确;
c=5,实轴长为4,可得a=2,b=,所以双曲线C的方程为-=1,所以D不正确;故选ABC.
【方法技巧】
已知双曲线的方程讨论其几何性质时,需先看所给方程是否为标准方程,若不是,需先把方程化为标准方程,然后由标准方程确定焦点所在的坐标轴,找准a和b,才能正确地写出焦点坐标、顶点坐标等.注意与椭圆的相关几何性质进行比较.
探究2 求双曲线的离心率
【例2】(1)设a>1,则双曲线-=1的离心率e的取值范围是( )
A.(,2) B.(,) C.(2,5) D.(2,)
(2)中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(4,-2),则它的离心率为( )
A. B. C. D.
(3)设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为________.
【答案】(1)B (2)D
【解析】(1)由题意得,双曲线的离心率e2=2==1+2,因为是减函数,所以当a>1时,0<<1,所以2(2)由题意知,过点(4,-2)的渐近线的方程为y=-x,
∴-2=-·4,∴a=2b.
方法一 设b=k,则a=2k,c=k,∴e===.
方法二 e2=+1=+1=,故e=.
(3)不妨设焦点F(c,0),虚轴的端点B(0,b),则kFB=-.又渐近线的斜率为±,所以由直线垂直得-·=-1(斜率为-的直线显然不符合),即b2=ac.
又c2-a2=b2,故c2-a2=ac,两边同除以a2,得方程e2-e-1=0,解得e=(负值舍去).
【方法技巧】
求双曲线的离心率或其取值范围的思路
1.求解双曲线的离心率一般有两种方法.
(1)由条件寻找a,c所满足的等式,常用的公式变形为e===,其中a>0,b>0.
(2)依据条件列出含a,c的齐次方程,利用e=转化为含e或e2的方程,解方程即可,注意依据e>1对所得解进行取舍.
2.求双曲线离心率的取值范围,关键是根据条件得到不等关系,并想办法转化为关于a,b,c的不等关系,结合c2=a2+b2和=e得到关于e的不等式,然后求解.在建立不等式求e时,经常用到结论:双曲线上一点到相应焦点距离的最小值为c-a.
双曲线的离心率常以渐近线为载体进行命题,注意二者参数之间的转化.
探究3 求双曲线的渐近线
【例3】(1)已知椭圆E:+=1与双曲线C:-y2=1(a>0)有共同的焦点,则双曲线C的渐近线方程为( )
A.y=±x B.y=±x C.y=±x D.y=±x
(2)在平面直角坐标系xOy中,若双曲线x2-=1(b>0)经过点(3,4),则该双曲线的渐近线方程是________.
【答案】(1)B (2)y=±x
【解析】(1)椭圆E的焦点为F1(2,0),F2(-2,0),所以双曲线C的焦点为F1(2,0),F2(-2,0),
则在双曲线C中:c=2,b=1,a==,所以双曲线C的渐近线方程为:y=±x=±x.故选B.
(2)由题意知:32-=1,解得b=.所以双曲线的渐近线方程是y=±bx=±x.
【方法技巧】
由双曲线的标准方程求它的渐近线方程时,可以把双曲线的标准方程-=1或-=1(a>0,b>0)中等号右边的“1”改成“0”,然后分解因式即可得到渐近线的方程±=0或±=0.
【变式训练】
1. (多选)在平面直角坐标系xOy中,已知双曲线-=1,则( )
A.实轴长为2
B.渐近线方程为y=±x
C.离心率为2
D.一条渐近线与准线的交点到另一条渐近线的距离为3
【答案】BC
【解析】(1)由双曲线的方程可得,a2=4,b2=12,c2=a2+b2=16,所以a=2,b=2,c=4;
所以实轴长2a=4,离心率=2,渐近线方程为y=±x=±x,所以A不正确;B,C正确;
因为准线方程为x==1,设渐近线y=x与渐近线的交点为A,两个方程联立可得A(1,),另一条渐近线的方程为:x+y=0,所以A到它的距离为d==,所以D不正确.
(2)已知F为双曲线E:-=1(a>0,b>0)的右焦点,过点F向双曲线E的一条渐近线引垂线,垂足为A,且交另一条渐近线于点B,若|OF|=|FB|,则双曲线E的离心率是________.
【答案】
【解析】双曲线E:-=1的渐近方程为y=±x,若|OF|=|FB|,可得在直角三角形OAB中,由∠AOF=∠BOF=∠ABO=30°,
可得=tan30°=,∴==1+=1+=,∴e=.
题型三 直线与双曲线的位置关系
【例4】(1)直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A,B,则实数k的取值范围为________.
(2)双曲线的中心在原点,一个焦点坐标为F(,0),直线y=x-1与双曲线相交于M,N两点,线段MN中点的横坐标为-,则双曲线的方程为________.
【答案】(1)(-2,-) (2)-=1
【解析】(1)联立方程组得(k2-2)x2+2kx+2=0
则解得-2(2)由题意知MN中点的坐标为,
设双曲线的方程为-=1(a>0),M(x1,y1),N(x2,y2),则
-=1 ①,
-=1 ②. ①-②得=,即
=·,所以=,解得a2=2,故双曲线的方程为-=1.
【方法技巧】
解决有关直线与双曲线的位置关系的问题时,还要关注直线交于双曲线两支中哪一支的问题,从而确定变量x和y的隐含范围.
直线与双曲线的位置关系的判断方法
1.代数法
将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中,要注意x2项或y2项的系数是否为零,否则容易漏解.
2.数形结合法
判断直线与双曲线的交点情况时,可以根据双曲线的渐近线的斜率与直线的斜率的大小关系,确定直线与双曲线的位置关系.
与双曲线有关的中点弦问题的解题思路
与椭圆的中点弦问题一样,求解与双曲线有关的中点弦问题也是利用点差法及设而不求的思想.另外,需注意:过椭圆内一点作直线,与椭圆交于两点,使这点为弦的中点,这样的直线一定存在,但在双曲线中,则不能确定这样的直线是否存在,要注意检验.
【变式训练】
1.设双曲线C:-y2=1(a>0)与直线l:x+y=1相交于两个不同的点,则双曲线C的离心率e的取值范围为( )
A. (, ) B.(,+∞) C. (,+∞) D. (,)∪(,+∞)
(2)已知双曲线-y2=1,则过点A(3,-1),且被点A平分的双曲线的弦MN所在直线方程是________.
【答案】(1)D (2)3x+4y-5=0.
【解析】(1)由得(1-a2)x2+2a2x-2a2=0
则解得a2∈(0,1)∪(1,2)
又e=,∴a2=
从而e∈∪(,+∞),故选D.
(2)设M(x1,y1),N(x2,y2),
则两式相减得=y-y
所以=.
因为点A平分弦MN,所以x1+x2=6,y1+y2=-2.
所以kMN===-.
所以双曲线的弦MN所在直线的方程为y+1=-(x-3),即3x+4y-5=0.
易错辨析 忽略对焦点所在轴的讨论致误
【例5】已知双曲线的渐近线方程是y=±x,焦距为2,求双曲线的标准方程.
【解析】当双曲线的焦点在x轴上时,由
解得所以所求双曲线的标准方程为-=1.
当双曲线的焦点在y轴上时,由
解得所以所求双曲线的标准方程为-=1.
故所求双曲线的标准方程为-=1或-=1.
【易错警示】
易错原因 纠错心得
误认为焦点一定在x轴上,得到答案:-=1,而漏掉焦点在y轴上的情况. 当题目条件没有明确双曲线的焦点所在轴时,应分两种情况进行讨论.同时注意两种情况下,渐近线方程是有区别的:焦点在x轴上时,渐近线方程为y=±x;焦点在y轴上时,渐近线方程为y=±x.
1.(2021·福建省武平县第一中学高二月考)双曲线2x2-y2=8的实轴长是( )
A.2 B.2
C.4 D.4
【答案】C
【解析】双曲线方程可变形为-=1,所以a2=4,a=2,从而2a=4,故选C.
2.(2021·江苏省响水中学高二期中)如果椭圆+=1(a>0,b>0)的离心率为,那么双曲线-=1的离心率为( )
A. B.
C. D.2
【答案】A
【解析】由已知椭圆的离心率为,得=,∴a2=4b2.∴e2===.∴双曲线的离心率e=.
3.(2021·全国高二课时练习)若双曲线与椭圆+=1有相同的焦点,它的一条渐近线方程为y=-x,则双曲线的方程为( )
A.y2-x2=96 B.y2-x2=160
C.y2-x2=80 D.y2-x2=24
【答案】D
【解析】设双曲线方程为x2-y2=λ(λ≠0),因为双曲线与椭圆有相同的焦点,且焦点为(0,±4),所以λ<0,且-2λ=(4)2,得λ=-24.故选D.
4.(2021·宁夏长庆高级中学高二期中(文))设双曲线(,),离心率,右焦点,方程的两个实数根分别为,,则点与圆的位置关系( )
A.在圆外 B.在圆 C.在圆内 D.不确定
【答案】C
【解析】因为双曲线(,)的离心率
所以,所以
所以,即点在圆的内部,故选:C
5.(多选)(2021山东省潍坊一中高二期中考试)已知F1,F2分别是双曲线C:y2-x2=1的上、下焦点,点P是其一条渐近线上一点,且以线段F1F2为直径的圆经过点P,则( )
A.双曲线C的渐近线方程为y=±x
B.以F1F2为直径的圆的方程为x2+y2=1
C.点P的横坐标为±1
D.△PF1F2的面积为
【答案】ACD
【解析】等轴双曲线C:y2-x2=1的渐近线方程为y=±x,故A正确.由双曲线的方程可知|F1F2|=2,所以以F1F2为直径的圆的方程为x2+y2=2,故B错误.点P(x0,y0)在圆x2+y2=2上,不妨设点P(x0,y0)在直线y=x上,所以解得|x0|=1,则点P的横坐标为±1,故C正确.由上述分析可得△PF1F2的面积为×2×1=,故D正确.故选A、C、D.
6.(2021·沭阳县修远中学高二月考)已知点(2,3)在双曲线C:-=1(a>0,b>0)上,C的焦距为4,则它的离心率为________.
【答案】2
【解析】由题意知-=1,c2=a2+b2=4,解得a=1,所以e==2.
7.(2021·江苏马坝高中高二月考)设双曲线C经过点(2,2),且与-x2=1具有相同的渐近线,则C的方程为________,渐近线方程为________.
【答案】-=1 y=±2x
【解析】设双曲线C的方程为-x2=λ.将点(2,2)的坐标代入,得λ=-3,∴双曲线C的方程为-=1.令-x2=0,得y=±2x,即渐近线方程为y=±2x.
8.(2021·江苏启东中学高二期中)已知定点A,B且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值为________.
【答案】
【解析】如图所示,点P是以A,B为焦点的双曲线的右支上的点,当P在M处时,|PA|最小,最小值为a+c=+2=.
9.(2021·甘肃省武威第一中学高二期中)已知双曲线E与双曲线-=1共渐近线,且过点A(2,-3).若双曲线M以双曲线E的实轴为虚轴,虚轴为实轴,试求双曲线M的标准方程.
【解析】由题意,设双曲线E的方程为-=t(t≠0).
∵点A(2,-3)在双曲线E上,∴-=t,
∴t=-,∴双曲线E的标准方程为-=1.
又双曲线M与双曲线E互为共轭双曲线,
∴双曲线M的标准方程为-=1.
10((2021·江西南昌市·南昌十中高二期中(文))已知双曲线.
(1)求与双曲线有共同的渐近线,且过点的双曲线的标准方程;
(2)若直线与双曲线交于A、B两点,且A、B的中点坐标为(1,1),求直线的斜率.
【解析】(1)因为所求双曲线与双曲线有共同的渐近线,
所以设所求双曲线方程为,代入,得,
所以所求双曲线方程为;
(2)设,因为、在双曲线上,
所以,(1)-(2)得,
因为A、B的中点坐标为(1,1),即,
所以.
11.(2021·河北承德第一中学高二月考)已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A,B两点,且AB的中点为N(-12,-15),则E的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
【答案】B
【解析】设双曲线的标准方程为-=1(a>0,b>0),由题意知c=3,a2+b2=9,
设A(x1,y1),B(x2,y2)则有
两式作差得===,
又AB的斜率是=1,
所以4b2=5a2,代入a2+b2=9得a2=4,b2=5,
所以双曲线标准方程是-=1.
12.(多选)(2021·东湖区·江西师大附中高二期中(理))定义:以双曲线的实轴为虚轴,虚轴为实轴的双曲线与原双曲线互为共轭双曲线,以下关于共轭双曲线的结论正确的有( )
A.与共轭的双曲线是;
B.互为共轭的双曲线渐近线不相同;
C.互为共轭的双曲线的离心率为,则;
D.互为共轭的双曲线的4个焦点在同一圆上.
【答案】ABCD
【解析】根据共轭双曲线的定义可知,与共轭的双曲线是,故A正确;
由双曲线的方程可得,的渐近线方程均为,B正确
由双曲线方程可得,,所以,
上式整理得,根据、都是大于1的正数,得,
两边约去,得,时等号成立,故C正确;
的焦点坐标为,的焦点为,
4个焦点在以原点为圆心,以为半径的圆上,D正确.,故选ABCD。
13.(2021·怀仁市第一中学校云东校区高二月考)已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线l与双曲线的右支有且只有一个交点,则此双曲线的离心率e的取值范围是_____________________.
【答案】 [2,+∞)
【解析】由题意,知≥,则≥3,所以c2-a2≥3a2,
即c2≥4a2,所以e2=≥4,所以e≥2.
14.(2021·四川省绵阳南山中学高二期中)若双曲线E:-y2=1(a>0)的离心率等于,直线y=kx-1与双曲线E的右支交于A,B两点.
(1)求k的取值范围;
(2)若|AB|=6,求k的值.
【解析】(1)由得故双曲线E的方程为x2-y2=1.
设A(x1,y1),B(x2,y2),
由得(1-k2)x2+2kx-2=0.①
∵直线与双曲线右支交于A,B两点,故
即
∴1<k<.
(2)由①得x1+x2=,x1x2=,
∴|AB|=·
=2=6,
整理得28k4-55k2+25=0,
∴k2=或k2=.
又1<k<,∴k=.
15.(2021·邯郸市永年区第一中学高二期末)双曲线C的中心在原点,右焦点为F,渐近线方程为y=±x.
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线C交于A,B两点,问:当k为何值时,以AB为直径的圆过原点?
【解析】(1)设双曲线的方程是-=1(a>0,b>0),则c=,=.又∵c2=a2+b2,∴b2=1,a2=.
∴双曲线的方程是3x2-y2=1.
(2)由得(3-k2)x2-2kx-2=0.
由Δ>0,且3-k2≠0,得-<k<,且k≠±.
设A(x1,y1),B(x2,y2).
∵以AB为直径的圆过原点,∴OA⊥OB.
∴x1x2+y1y2=0.
又∵x1+x2=,x1x2=,
∴y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=1,
∴+1=0,解得k=±1.
故当k=±1时,以AB为直径的圆过原点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.2.2双曲线的简单几何性质
要点一 双曲线的几何性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
性质 图形
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
性质 范围 或,y∈R 或,x∈R
对称性 对称轴:坐标轴;对称中心:远点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段,长:;虚轴:线段,长:2b;半实轴长:,半虚轴长:b
离心率 e=∈
渐近线 y=±x y=±x
【方法技巧】
(1)双曲线的范围说明双曲线是非封闭曲线,而椭圆则是封闭曲线.
(2)当|x|无限增大时,|y|也无限增大,即双曲线的各支是向外无限延展的.
(3)双曲线的渐近线决定了双曲线的形状.由双曲线的对称性可知,当双曲线的两支向外无限延伸时,双曲线与两条渐近线无限接近,但永远不会相交.
(4)双曲线形状与e的关系.
由于== =,因此e越大,渐近线的斜率的绝对值就越大,双曲线的开口就越大.
要点二 等轴双曲线
实轴和虚轴等长的双曲线叫等轴双曲线,它的渐近线是,离心率为.
【答疑解惑】
教材P126思考
通过比较例5与椭圆一节中的例6可以发现.动点到定点的距离和它到定直线的距离之比是常数,若这个常数大于0小于1,则动点的轨迹是椭圆;若这个常数大于1,则动点的轨迹是双曲线.
看大小,焦点随着大的跑”.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)双曲线的离心率越大,双曲线的开口越开阔.( )
(2)以y=±2x为渐近线的双曲线有2条.( )
(3)方程-=1(a>0,b>0)的渐近线方程为y=±x.( )
(4)离心率e越大,双曲线-=1的渐近线的斜率绝对值越大.( )
【答案】(1)√(2)×(3)×(4)×
2.实轴长为2,虚轴长为4的双曲线的标准方程是( )
A.x2-=1
B.y2-=1
C.-=1或-=1
D.x2-=1或y2-=1
【答案】D
【解析】由题意知2a=2,2b=4∴a=1,b=2,∴a2=1,b2=4又双曲线的焦点位置不确定,故选D.
3.双曲线-y2=1的渐近线方程是( )
A.y=±x B.y=±x C.y=±2x D.y=±x
【答案】B
【解析】由双曲线方程得:a=,b=1,∴渐近线方程为:y=±x=±x.故选B.
4.若双曲线-=1(a>0,b>0)的两条渐近线互相垂直,则该双曲线的离心率是________.
【答案】
【解析】由题意知渐近线与x轴的夹角θ=∴=tan=1∴e==
题型一 由双曲线的几何性质求其标准方程
1.已知双曲线-=1(a>0,b>0)的右焦点为F,点A在双曲线的渐近线上,△OAF是边长为2的等边三角形(O为原点),则双曲线的方程为( )
A.-=1 B.-=1 C.-y2=1 D.x2-=1
【答案】D
【解析】不妨设点A在第一象限,由题意可知c=2,点A的坐标为(1,),所以=,又c2=a2+b2,所以a2=1,b2=3,故所求双曲线的方程为x2-=1,故选D.
2.焦点为(0,6),且与双曲线-y2=1有相同的渐近线的双曲线方程是________.
【答案】-=1
【解析】由-y2=1,得双曲线的渐近线为y=±x.设双曲线方程为:-y2=λ(λ<0),∴-=1,∴-λ-2λ=36,∴λ=-12.
故双曲线方程为-=1.
3.过点(2,0),与双曲线-=1离心率相等的双曲线方程为________.
【答案】-y2=1
【解析】当所求双曲线的焦点在x轴上时,可设其方程为-=λ(λ>0),将点(2,0)的坐标代入方程得λ=,故所求双曲线的标准方程为-y2=1;
当所求双曲线的焦点在y轴上时,可设其方程为-=λ(λ>0),将点(2,0)的坐标代入方程得λ=-<0(舍去).综上可知,所求双曲线的标准方程为-y2=1.
4.与椭圆+=1有公共焦点,离心率为的双曲线方程为________.
【答案】-=1
【解析】方法一 由椭圆方程可得焦点坐标为(-3,0),(3,0),即c=3且焦点在x轴上.
设双曲线的标准方程为-=1(a>0,b>0).
因为e==,所以a=2,则b2=c2-a2=5,故所求双曲线的标准方程为-=1.
方法二 因为椭圆焦点在x轴上,所以可设双曲线的标准方程为-=1(16<λ<25).
因为e=,所以=-1,解得λ=21.故所求双曲线的标准方程为-=1.
【方法技巧】
由几何性质求双曲线标准方程的解题思路
1.由双曲线的几何性质求双曲线的标准方程,一般用待定系数法.当双曲线的焦点不明确时,方程可能有两种形式,此时应注意分类讨论,为了避免讨论,也可设双曲线的方程为mx2-ny2=1(mn>0).
2.常见双曲线方程的设法
(1)渐近线为y=±x的双曲线方程可设为-=λ(λ≠0,m>0,n>0);如果两条渐近线的方程为Ax±By=0,那么双曲线的方程可设为A2x2-B2y2=m(m≠0,A>0,B>0).
(2)与双曲线-=1或-=1(a>0,b>0)共渐近线的双曲线方程可设为-=λ或-=λ(λ≠0).
(3)与双曲线-=1(a>0,b>0)离心率相等的双曲线系方程可设为-=λ(λ>0)或-=λ(λ>0),这是因为由离心率不能确定焦点位置.
(4)与椭圆+=1(a>b>0)共焦点的双曲线系方程可设为-=1(b2<λ
探究1 利用方程求解几何性质
【例1】(多选)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-5,0),F2(5,0),则能使双曲线C的方程为-=1的是( )
A.离心率为 B.双曲线过点(5,)
C.渐近线方程为3x±4y=0 D.实轴长为4
【答案】ABC
【解析】双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-5,0),F2(5,0).
可得c=5,如果离心率为:.可得a=4,则b=3,所以,双曲线C的方程为-=1,所以A正确;
c=5,双曲线过点,可得解得a=4,b=3,所以双曲线C的方程为-=1,所以B正确;
c=5,渐近线方程为3x±4y=0,可得=,a2+b2=25,
解得a=4,b=3,所以双曲线C的方程为-=1,所以C正确;
c=5,实轴长为4,可得a=2,b=,所以双曲线C的方程为-=1,所以D不正确;故选ABC.
【方法技巧】
已知双曲线的方程讨论其几何性质时,需先看所给方程是否为标准方程,若不是,需先把方程化为标准方程,然后由标准方程确定焦点所在的坐标轴,找准a和b,才能正确地写出焦点坐标、顶点坐标等.注意与椭圆的相关几何性质进行比较.
探究2 求双曲线的离心率
【例2】(1)设a>1,则双曲线-=1的离心率e的取值范围是( )
A.(,2) B.(,) C.(2,5) D.(2,)
(2)中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(4,-2),则它的离心率为( )
A. B. C. D.
(3)设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为________.
【答案】(1)B (2)D
【解析】(1)由题意得,双曲线的离心率e2=2==1+2,因为是减函数,所以当a>1时,0<<1,所以2
∴-2=-·4,∴a=2b.
方法一 设b=k,则a=2k,c=k,∴e===.
方法二 e2=+1=+1=,故e=.
(3)不妨设焦点F(c,0),虚轴的端点B(0,b),则kFB=-.又渐近线的斜率为±,所以由直线垂直得-·=-1(斜率为-的直线显然不符合),即b2=ac.
又c2-a2=b2,故c2-a2=ac,两边同除以a2,得方程e2-e-1=0,解得e=(负值舍去).
【方法技巧】
求双曲线的离心率或其取值范围的思路
1.求解双曲线的离心率一般有两种方法.
(1)由条件寻找a,c所满足的等式,常用的公式变形为e===,其中a>0,b>0.
(2)依据条件列出含a,c的齐次方程,利用e=转化为含e或e2的方程,解方程即可,注意依据e>1对所得解进行取舍.
2.求双曲线离心率的取值范围,关键是根据条件得到不等关系,并想办法转化为关于a,b,c的不等关系,结合c2=a2+b2和=e得到关于e的不等式,然后求解.在建立不等式求e时,经常用到结论:双曲线上一点到相应焦点距离的最小值为c-a.
双曲线的离心率常以渐近线为载体进行命题,注意二者参数之间的转化.
探究3 求双曲线的渐近线
【例3】(1)已知椭圆E:+=1与双曲线C:-y2=1(a>0)有共同的焦点,则双曲线C的渐近线方程为( )
A.y=±x B.y=±x C.y=±x D.y=±x
(2)在平面直角坐标系xOy中,若双曲线x2-=1(b>0)经过点(3,4),则该双曲线的渐近线方程是________.
【答案】(1)B (2)y=±x
【解析】(1)椭圆E的焦点为F1(2,0),F2(-2,0),所以双曲线C的焦点为F1(2,0),F2(-2,0),
则在双曲线C中:c=2,b=1,a==,所以双曲线C的渐近线方程为:y=±x=±x.故选B.
(2)由题意知:32-=1,解得b=.所以双曲线的渐近线方程是y=±bx=±x.
【方法技巧】
由双曲线的标准方程求它的渐近线方程时,可以把双曲线的标准方程-=1或-=1(a>0,b>0)中等号右边的“1”改成“0”,然后分解因式即可得到渐近线的方程±=0或±=0.
【变式训练】
1. (多选)在平面直角坐标系xOy中,已知双曲线-=1,则( )
A.实轴长为2
B.渐近线方程为y=±x
C.离心率为2
D.一条渐近线与准线的交点到另一条渐近线的距离为3
【答案】BC
【解析】(1)由双曲线的方程可得,a2=4,b2=12,c2=a2+b2=16,所以a=2,b=2,c=4;
所以实轴长2a=4,离心率=2,渐近线方程为y=±x=±x,所以A不正确;B,C正确;
因为准线方程为x==1,设渐近线y=x与渐近线的交点为A,两个方程联立可得A(1,),另一条渐近线的方程为:x+y=0,所以A到它的距离为d==,所以D不正确.
(2)已知F为双曲线E:-=1(a>0,b>0)的右焦点,过点F向双曲线E的一条渐近线引垂线,垂足为A,且交另一条渐近线于点B,若|OF|=|FB|,则双曲线E的离心率是________.
【答案】
【解析】双曲线E:-=1的渐近方程为y=±x,若|OF|=|FB|,可得在直角三角形OAB中,由∠AOF=∠BOF=∠ABO=30°,
可得=tan30°=,∴==1+=1+=,∴e=.
题型三 直线与双曲线的位置关系
【例4】(1)直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A,B,则实数k的取值范围为________.
(2)双曲线的中心在原点,一个焦点坐标为F(,0),直线y=x-1与双曲线相交于M,N两点,线段MN中点的横坐标为-,则双曲线的方程为________.
【答案】(1)(-2,-) (2)-=1
【解析】(1)联立方程组得(k2-2)x2+2kx+2=0
则解得-2
设双曲线的方程为-=1(a>0),M(x1,y1),N(x2,y2),则
-=1 ①,
-=1 ②. ①-②得=,即
=·,所以=,解得a2=2,故双曲线的方程为-=1.
【方法技巧】
解决有关直线与双曲线的位置关系的问题时,还要关注直线交于双曲线两支中哪一支的问题,从而确定变量x和y的隐含范围.
直线与双曲线的位置关系的判断方法
1.代数法
将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中,要注意x2项或y2项的系数是否为零,否则容易漏解.
2.数形结合法
判断直线与双曲线的交点情况时,可以根据双曲线的渐近线的斜率与直线的斜率的大小关系,确定直线与双曲线的位置关系.
与双曲线有关的中点弦问题的解题思路
与椭圆的中点弦问题一样,求解与双曲线有关的中点弦问题也是利用点差法及设而不求的思想.另外,需注意:过椭圆内一点作直线,与椭圆交于两点,使这点为弦的中点,这样的直线一定存在,但在双曲线中,则不能确定这样的直线是否存在,要注意检验.
【变式训练】
1.设双曲线C:-y2=1(a>0)与直线l:x+y=1相交于两个不同的点,则双曲线C的离心率e的取值范围为( )
A. (, ) B.(,+∞) C. (,+∞) D. (,)∪(,+∞)
(2)已知双曲线-y2=1,则过点A(3,-1),且被点A平分的双曲线的弦MN所在直线方程是________.
【答案】(1)D (2)3x+4y-5=0.
【解析】(1)由得(1-a2)x2+2a2x-2a2=0
则解得a2∈(0,1)∪(1,2)
又e=,∴a2=
从而e∈∪(,+∞),故选D.
(2)设M(x1,y1),N(x2,y2),
则两式相减得=y-y
所以=.
因为点A平分弦MN,所以x1+x2=6,y1+y2=-2.
所以kMN===-.
所以双曲线的弦MN所在直线的方程为y+1=-(x-3),即3x+4y-5=0.
易错辨析 忽略对焦点所在轴的讨论致误
【例5】已知双曲线的渐近线方程是y=±x,焦距为2,求双曲线的标准方程.
【解析】当双曲线的焦点在x轴上时,由
解得所以所求双曲线的标准方程为-=1.
当双曲线的焦点在y轴上时,由
解得所以所求双曲线的标准方程为-=1.
故所求双曲线的标准方程为-=1或-=1.
【易错警示】
易错原因 纠错心得
误认为焦点一定在x轴上,得到答案:-=1,而漏掉焦点在y轴上的情况. 当题目条件没有明确双曲线的焦点所在轴时,应分两种情况进行讨论.同时注意两种情况下,渐近线方程是有区别的:焦点在x轴上时,渐近线方程为y=±x;焦点在y轴上时,渐近线方程为y=±x.
1.(2021·福建省武平县第一中学高二月考)双曲线2x2-y2=8的实轴长是( )
A.2 B.2
C.4 D.4
【答案】C
【解析】双曲线方程可变形为-=1,所以a2=4,a=2,从而2a=4,故选C.
2.(2021·江苏省响水中学高二期中)如果椭圆+=1(a>0,b>0)的离心率为,那么双曲线-=1的离心率为( )
A. B.
C. D.2
【答案】A
【解析】由已知椭圆的离心率为,得=,∴a2=4b2.∴e2===.∴双曲线的离心率e=.
3.(2021·全国高二课时练习)若双曲线与椭圆+=1有相同的焦点,它的一条渐近线方程为y=-x,则双曲线的方程为( )
A.y2-x2=96 B.y2-x2=160
C.y2-x2=80 D.y2-x2=24
【答案】D
【解析】设双曲线方程为x2-y2=λ(λ≠0),因为双曲线与椭圆有相同的焦点,且焦点为(0,±4),所以λ<0,且-2λ=(4)2,得λ=-24.故选D.
4.(2021·宁夏长庆高级中学高二期中(文))设双曲线(,),离心率,右焦点,方程的两个实数根分别为,,则点与圆的位置关系( )
A.在圆外 B.在圆 C.在圆内 D.不确定
【答案】C
【解析】因为双曲线(,)的离心率
所以,所以
所以,即点在圆的内部,故选:C
5.(多选)(2021山东省潍坊一中高二期中考试)已知F1,F2分别是双曲线C:y2-x2=1的上、下焦点,点P是其一条渐近线上一点,且以线段F1F2为直径的圆经过点P,则( )
A.双曲线C的渐近线方程为y=±x
B.以F1F2为直径的圆的方程为x2+y2=1
C.点P的横坐标为±1
D.△PF1F2的面积为
【答案】ACD
【解析】等轴双曲线C:y2-x2=1的渐近线方程为y=±x,故A正确.由双曲线的方程可知|F1F2|=2,所以以F1F2为直径的圆的方程为x2+y2=2,故B错误.点P(x0,y0)在圆x2+y2=2上,不妨设点P(x0,y0)在直线y=x上,所以解得|x0|=1,则点P的横坐标为±1,故C正确.由上述分析可得△PF1F2的面积为×2×1=,故D正确.故选A、C、D.
6.(2021·沭阳县修远中学高二月考)已知点(2,3)在双曲线C:-=1(a>0,b>0)上,C的焦距为4,则它的离心率为________.
【答案】2
【解析】由题意知-=1,c2=a2+b2=4,解得a=1,所以e==2.
7.(2021·江苏马坝高中高二月考)设双曲线C经过点(2,2),且与-x2=1具有相同的渐近线,则C的方程为________,渐近线方程为________.
【答案】-=1 y=±2x
【解析】设双曲线C的方程为-x2=λ.将点(2,2)的坐标代入,得λ=-3,∴双曲线C的方程为-=1.令-x2=0,得y=±2x,即渐近线方程为y=±2x.
8.(2021·江苏启东中学高二期中)已知定点A,B且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值为________.
【答案】
【解析】如图所示,点P是以A,B为焦点的双曲线的右支上的点,当P在M处时,|PA|最小,最小值为a+c=+2=.
9.(2021·甘肃省武威第一中学高二期中)已知双曲线E与双曲线-=1共渐近线,且过点A(2,-3).若双曲线M以双曲线E的实轴为虚轴,虚轴为实轴,试求双曲线M的标准方程.
【解析】由题意,设双曲线E的方程为-=t(t≠0).
∵点A(2,-3)在双曲线E上,∴-=t,
∴t=-,∴双曲线E的标准方程为-=1.
又双曲线M与双曲线E互为共轭双曲线,
∴双曲线M的标准方程为-=1.
10((2021·江西南昌市·南昌十中高二期中(文))已知双曲线.
(1)求与双曲线有共同的渐近线,且过点的双曲线的标准方程;
(2)若直线与双曲线交于A、B两点,且A、B的中点坐标为(1,1),求直线的斜率.
【解析】(1)因为所求双曲线与双曲线有共同的渐近线,
所以设所求双曲线方程为,代入,得,
所以所求双曲线方程为;
(2)设,因为、在双曲线上,
所以,(1)-(2)得,
因为A、B的中点坐标为(1,1),即,
所以.
11.(2021·河北承德第一中学高二月考)已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A,B两点,且AB的中点为N(-12,-15),则E的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
【答案】B
【解析】设双曲线的标准方程为-=1(a>0,b>0),由题意知c=3,a2+b2=9,
设A(x1,y1),B(x2,y2)则有
两式作差得===,
又AB的斜率是=1,
所以4b2=5a2,代入a2+b2=9得a2=4,b2=5,
所以双曲线标准方程是-=1.
12.(多选)(2021·东湖区·江西师大附中高二期中(理))定义:以双曲线的实轴为虚轴,虚轴为实轴的双曲线与原双曲线互为共轭双曲线,以下关于共轭双曲线的结论正确的有( )
A.与共轭的双曲线是;
B.互为共轭的双曲线渐近线不相同;
C.互为共轭的双曲线的离心率为,则;
D.互为共轭的双曲线的4个焦点在同一圆上.
【答案】ABCD
【解析】根据共轭双曲线的定义可知,与共轭的双曲线是,故A正确;
由双曲线的方程可得,的渐近线方程均为,B正确
由双曲线方程可得,,所以,
上式整理得,根据、都是大于1的正数,得,
两边约去,得,时等号成立,故C正确;
的焦点坐标为,的焦点为,
4个焦点在以原点为圆心,以为半径的圆上,D正确.,故选ABCD。
13.(2021·怀仁市第一中学校云东校区高二月考)已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线l与双曲线的右支有且只有一个交点,则此双曲线的离心率e的取值范围是_____________________.
【答案】 [2,+∞)
【解析】由题意,知≥,则≥3,所以c2-a2≥3a2,
即c2≥4a2,所以e2=≥4,所以e≥2.
14.(2021·四川省绵阳南山中学高二期中)若双曲线E:-y2=1(a>0)的离心率等于,直线y=kx-1与双曲线E的右支交于A,B两点.
(1)求k的取值范围;
(2)若|AB|=6,求k的值.
【解析】(1)由得故双曲线E的方程为x2-y2=1.
设A(x1,y1),B(x2,y2),
由得(1-k2)x2+2kx-2=0.①
∵直线与双曲线右支交于A,B两点,故
即
∴1<k<.
(2)由①得x1+x2=,x1x2=,
∴|AB|=·
=2=6,
整理得28k4-55k2+25=0,
∴k2=或k2=.
又1<k<,∴k=.
15.(2021·邯郸市永年区第一中学高二期末)双曲线C的中心在原点,右焦点为F,渐近线方程为y=±x.
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线C交于A,B两点,问:当k为何值时,以AB为直径的圆过原点?
【解析】(1)设双曲线的方程是-=1(a>0,b>0),则c=,=.又∵c2=a2+b2,∴b2=1,a2=.
∴双曲线的方程是3x2-y2=1.
(2)由得(3-k2)x2-2kx-2=0.
由Δ>0,且3-k2≠0,得-<k<,且k≠±.
设A(x1,y1),B(x2,y2).
∵以AB为直径的圆过原点,∴OA⊥OB.
∴x1x2+y1y2=0.
又∵x1+x2=,x1x2=,
∴y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=1,
∴+1=0,解得k=±1.
故当k=±1时,以AB为直径的圆过原点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
