3.3.2抛物线及其标准方程(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 3.3.2抛物线及其标准方程(知识梳理+例题+变式+练习)(解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 994.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 07:55:39 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
3.3.2抛物线的简单几何性质
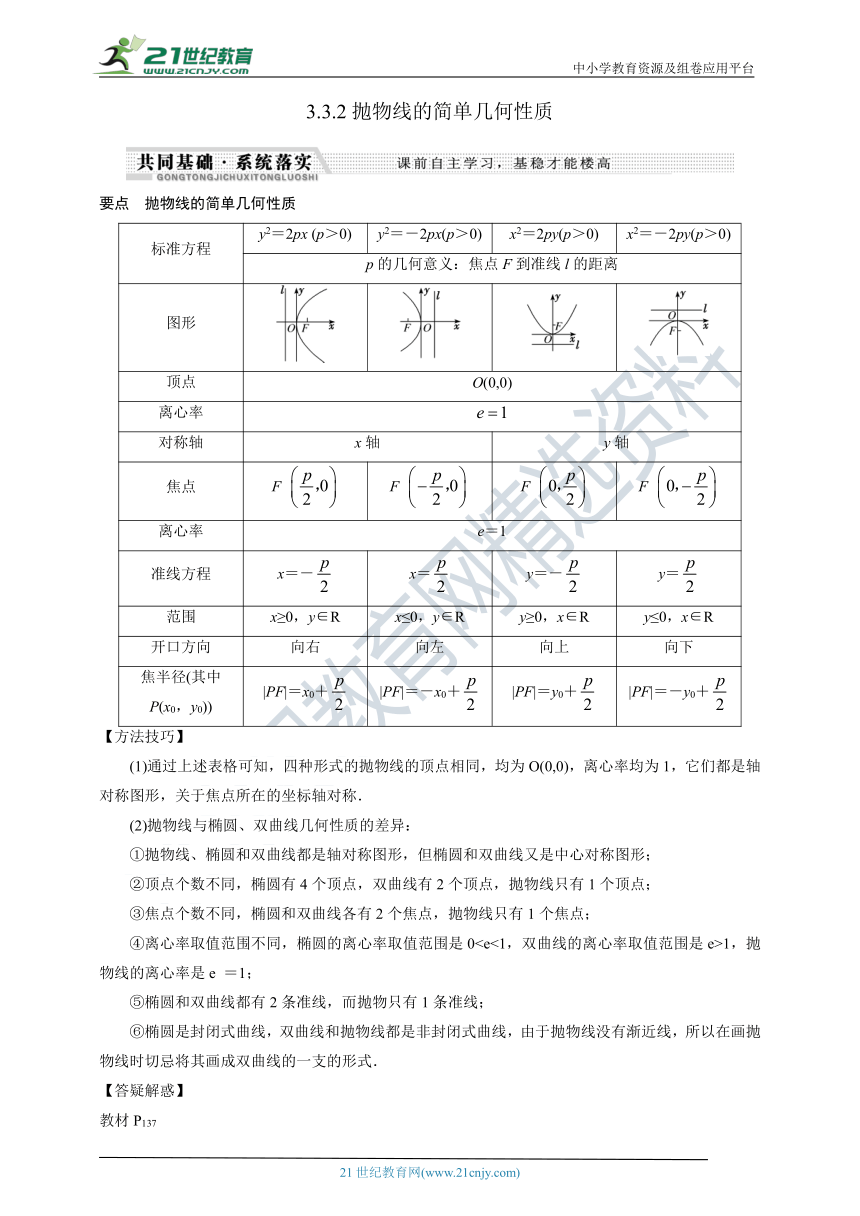
要点 抛物线的简单几何性质
标准方程 y2=2px (p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
p的几何意义:焦点F到准线l的距离
图形
顶点 O(0,0)
离心率
对称轴 x轴 y轴
焦点 F F F F
离心率 e=1
准线方程 x=- x= y=- y=
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
开口方向 向右 向左 向上 向下
焦半径(其中P(x0,y0)) |PF|=x0+ |PF|=-x0+ |PF|=y0+ |PF|=-y0+
【方法技巧】
(1)通过上述表格可知,四种形式的抛物线的顶点相同,均为O(0,0),离心率均为1,它们都是轴对称图形,关于焦点所在的坐标轴对称.
(2)抛物线与椭圆、双曲线几何性质的差异:
①抛物线、椭圆和双曲线都是轴对称图形,但椭圆和双曲线又是中心对称图形;
②顶点个数不同,椭圆有4个顶点,双曲线有2个顶点,抛物线只有1个顶点;
③焦点个数不同,椭圆和双曲线各有2个焦点,抛物线只有1个焦点;
④离心率取值范围不同,椭圆的离心率取值范围是01,抛物线的离心率是e =1;
⑤椭圆和双曲线都有2条准线,而抛物只有1条准线;
⑥椭圆是封闭式曲线,双曲线和抛物线都是非封闭式曲线,由于抛物线没有渐近线,所以在画抛物线时切忌将其画成双曲线的一支的形式.
【答疑解惑】
教材P137
建系如教材P136例5.设抛物线的方程为y2=2px,过焦点的直线方程为my=x-,由消去x,得y2-2pmy-p2=0.
设直线与抛物线的两交点为A(,y1),B(,y2),则由根与系数的关系,得y1y2=-p2.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)抛物线x2=2py(p>0)有一条对称轴为y轴.( )
(2)抛物线y=-x2的准线方程是x=.( )
(3)抛物线是中心对称图形.( )
(4)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线,共可作3条.( )
【答案】(1)√(2)×(3)×(4)√
2.顶点在原点,对称轴为y轴,顶点到准线的距离为4的抛物线方程是( )
A.x2=16y B.x2=8y C.x2=±8y D.x2=±16y
【答案】D
【解析】顶点在原点,对称轴为y轴的抛物线方程有两个:x2=-2py,x2=2py(p>0).由顶点到准线的距离为4知p=8,故所求抛物线方程为x2=16y,x2=-16y.故选D.
3.过抛物线y2=4x的焦点作直线交抛物于A(x1,y1),B(x2,y2)两点,若x1+x2=6,则|AB|=( )
A.10 B.8 C.6 D.4
【答案】B
【解析】|AB|=x1+x2+p=6+2=8.故选B.
4.已知过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,|AF|=2,则|BF|=________.
【答案】2
【解析】F(1,0),由抛物线定义得A点横坐标为1.∴AF⊥x轴,∴|BF|=|AF|=2.
题型一 由抛物线的几何性质求其方程
【例1】已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值、抛物线方程和准线方程.
【解析】解法一:由抛物线开口方向向下,可设抛物线方程为x2=-2py(p>0),则焦点为F.
因为M(m,-3)在抛物线上,且|MF|=5,
所以解得
所以抛物线方程为x2=-8y,m=±2,准线方程为y=2.
解法二:设抛物线方程为x2=-2py(p>0),则焦点为F,准线l:y=,如图所示,作MN⊥l,垂足为N,则|MN|=|MF|=5,而|MN|=3+,所以3+=5,即p=4.
又因为点M在抛物线上,所以m2=24,所以m=±2.
所以抛物线方程为x2=-8y,m=±2,准线方程为y=2.
【方法技巧】
1.代数法:将几何性质转化为坐标表达式,解方程(组)求出未知数.
2.几何法:将几何性质与抛物线定义相结合,采用几何法求出焦准距,从而得到抛物线的标准方程.
【变式训练】
1.边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A,B的抛物线方程是( )
A.y2=x B.y2=-x C.y2=±x D.y2=±x
【答案】C
【解析】设抛物线方程为y2=ax(a≠0).
又A(取点A在x轴上方),
则有=±a,解得a=±,所以抛物线方程为y2=±x.故选C.
2.已知抛物线的顶点在坐标原点,对称轴为x轴且与圆x2+y2=4相交的公共弦长等于2,则抛物线的方程为________.
【答案】(2)y2=3x或y2=-3x
【解析】(2)根据抛物线和圆的对称性知,其交点纵坐标为±,交点横坐标为±1,则抛物线过点(1,)或(-1,),设抛物线方程为
y2=2px或y2=-2px(p>0),
则2p=3,从而抛物线方程为y2=3x或y2=-3x.
题型二 由抛物线的方程研究其几何性质
【例2】已知等边三角形AOB的顶点A,B在抛物线y2=x上,O为坐标原点,顶点A到抛物线的焦点F的距离等于,则△AOB的面积为________.
【答案】3
【解析】∵△AOB是等边三角形,A、B在抛物线y2=x上,∴顶点A,B关于抛物线的对称轴(x轴)对称,
不妨设A(y0,)(y0>0),则B(y0,-).
由|AF|=y0+=,解得y0=3,∴=,
∴△AOB的边长|AB|=2=2,
∴△AOB的面积为×(2)2×=3.
【方法技巧】
把握三个要点,确定抛物线的简单几何性质
1.开口方向:由抛物线标准方程看其开口方向,关键是看准二次项是x还是y,一次项的系数是正还是负.
2.位置关系:顶点位于焦点和准线与坐标轴的交点中间,准线垂直于对称轴.
3.定值:焦点到准线的距离为|p|,过焦点垂直于对称轴的弦(又称为通径)长为2|p|.
【变式训练】
抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=________.
【答案】x2+=1
【解析】设P(x0,y0),Q(x,y),由中点坐标公式得∴又∵点P在椭圆+=1上,∴+=1,即x2+=1.
【答案】6
【解析】如图,在正三角形ABF中,DF=p,BD=p,则B点坐标为.又点B在双曲线上,故-=1.解得p=6.
题型三 直线与抛物线的位置关系
探究1 弦长问题
【例3】已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点.
(1)若|AF|=4,求点A的坐标;
(2)求线段AB的长的最小值.
【解析】由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).设A(x1,y1),B(x2,y2).
(1)由抛物线的定义可知,|AF|=x1+,从而x1=4-1=3.代入y2=4x,解得y1=±2.
∴点A的坐标为(3,2)或(3,-2).
(2)当直线l的斜率存在时,
设直线l的方程为y=k(x-1).
与抛物线方程联立,得
消去y,整理得k2x2-(2k2+4)x+k2=0.
∵直线与抛物线相交于A,B两点,
则k≠0,并设其两根为x1,x2,∴x1+x2=2+.
由抛物线的定义可知,|AB|=x1+x2+p=4+>4.
当直线l的斜率不存在时,直线l的方程为x=1,与抛物线相交于A(1,2),B(1,-2),此时|AB|=4,
∴|AB|≥4,即线段AB的长的最小值为4.
【方法技巧】
抛物线弦长的求解思路
1.当直线的斜率k存在且k≠0时,弦长公式为|AB|=|x1-x2|=|y1-y2|;当直线的斜率k=0时,只有抛物线的对称轴是y轴时弦长存在,弦长公式为|AB|=|x1-x2|;当直线的斜率k不存在时,只有抛物线的对称轴是x轴时弦长存在,弦长公式为|AB|=|y1-y2|.
2.焦点弦是特殊的弦,除了可以利用以上方法求解,还可以利用抛物线的定义转化为焦半径和焦点弦长问题处理.注意熟记抛物线的四种标准方程对应的焦点弦长公式.
探究2 中点弦问题
【例4】已知抛物线y2=2x,过点Q(2,1)作一条直线交抛物线于A,B两点,试求弦AB的中点的轨迹方程.
【分析】方法一:利用点差法,设点作差,要考虑斜率不存在的情况;
方法二:可设出斜率存在时的直线的方程,将其与抛物线方程联立,可得一元二次方程,利用根与系数的关系及中点坐标公式,消参即可得轨迹方程,同时要考虑斜率不存在的情况.
【解析】方法一 设A(x1,y1),B(x2,y2),弦AB的中点为M(x,y),则y1+y2=2y,当直线AB的斜率存在时,kAB==.
易知
①-②,得(y1+y2)(y1-y2)=2(x1-x2),
所以2y·=2,即2y·=2,即2=x-(y≠0).
当直线AB的斜率不存在,即AB⊥x轴时,AB的中点为(2,0),适合上式,故所求轨迹方程为2=x-.
方法二 当直线AB的斜率存在时,设直线AB的方程为y-1=k(x-2)(k≠0),由得y2-y+1-2k=0.则所以k∈(-∞,0)∪(0,+∞).
设A(x1,y1),B(x2,y2),AB的中点为P(x,y),则y1+y2=,y1y2=.
所以x1+x2=(y+y)=[(y1+y2)2-2y1y2]==.
则x==,y==,
消去k得2=x-(y≠0).
当直线AB的斜率不存在,即AB⊥x轴时,AB的中点为(2,0),适合上式.
故所求轨迹方程为2=x-.
【方法技巧】
(1)方法一中得到kAB的等式是为点差法做准备.
(2)方法一中因为用点差法求轨迹方程时用到了斜率,所以必须验证斜率不存在的情况.
(3)方法二中直线与抛物线相交于两点,隐含着条件Δ>0.
(4)方法二中求y1+y2及x1+x2是为利用中点坐标公式做准备.
【方法技巧】
解决中点弦问题的思路
解决中点弦问题的基本方法是点差法、利用根与系数的关系,直线与抛物线的方程联立时消y有时更简捷,此类问题还要注意斜率不存在的情况,避免漏解.一般地,已知抛物线y2=2px(p>0)上两点A(x1,y1),B(x2,y2)及AB的中点P(x0,y0),则kAB=.
直线AB的方程为y-y0=(x-x0).
线段AB的垂直平分线的方程为y-y0=-(x-x0).
【变式训练】
1.斜率为的直线经过抛物线x2=8y的焦点,且与抛物线相交于A,B两点,则线段AB的长为________.
【答案】10
【解析】(1)方法一 由题意设A(x1,y1),B(x2,y2),则对于抛物线x2=8y,焦点弦长|AB|=p+y1+y2=4+y1+y2.
因为抛物线x2=8y的焦点为(0,2),且直线AB的斜率为,所以直线AB的方程为y=x+2,代入抛物线方程x2=8y,消去x整理得y2-6y+4=0,从而y1+y2=6,所以|AB|=10.
故线段AB的长为10.
方法二 由题意设A(x1,y1),B(x2,y2).由题意得抛物线的焦点为(0,2),故直线AB的方程为y=x+2,即x-2y+4=0,
由消去y得x2-4x-16=0,
则x1+x2=4,x1x2=-16,代入弦长公式|AB|=,得|AB|=10.
2.已知斜率为k的直线l与抛物线C:y2=4x交于A、B两点,线段AB的中点为M(2,1),则直线l的方程为( )
A.2x-y-3=0 B.2x-y-5=0 C.x-2y=0 D.x-y-1=0
【答案】A
【解析】设A(x1,y1),B(x2,y2),则 ==2,所以k=2,因为直线过点M(2,1),所以直线l的方程为2x-y-3=0.故选A.
易错辨析 忽略直线与抛物线有一个公共点的特殊情况致误
【例5】(多选)过定点P(-1,1)且与抛物线y2=2x只有一个交点的直线l的方程为( )
A.y=-1 B.y=1 C.(-1)x-2y++1=0 D.(1+)x+2y+-1=0
【答案】BCD
【解析】(1)当直线l的斜率不存在时,显然不满足题意.
(2)当直线l的斜率存在时,
①若直线l与抛物线的对称轴平行,则直线l的方程为y=1,此时直线l与抛物线只有一个公共点.
②若直线l与抛物线的对称轴不平行,设直线l的方程为y-1=k(x+1)(k≠0)
即y=k(x+1)+1(k≠0)
由消去x,得ky2-2y+2k+2=0
由题意知Δ=4-4k(2k+2)=0,解得k=
故所求直线l的方程为:
(-1)x-2y++1=0或(1+)x+2y+-1=0
综上所述,所求直线l的方程为y=1或(-1)x-2y++1=0或(1+)x+2y+-1=0.故选BCD.
【易错提醒】
易错原因 纠错心得
本题易错的地方是只考虑直线l的斜率k存在且不为0时的情形,而忽略k不存在及直线l平行于抛物线的对称轴这两种情形. 在涉及直线与抛物线只有一个交点的问题时,应提防两处陷阱:一是直线与对称轴平行时,直线与抛物线只有一个交点,这是由Δ=0无法得到的(事实上,此时消元后对应的“一元二次”方程的“二次”项系数一定为零);二是若由Δ=0仅得到一条直线,则意味着斜率不存在的直线可能与抛物线相切(仅有一个交点),应检验斜率不存在的直线是否满足条件.
1.过抛物线y2=2px(p>0)的焦点,且垂直于x轴的弦为AB,O为抛物线的顶点,则∠AOB的度数( )
A.小于90° B.等于90°
C.大于90° D.不能确定
【答案】C
【解析】设抛物线y2=2px的焦点为F,则其坐标为,将x=代入抛物线的方程,解得A,B.在直角三角形AOF中,|OF|<|AF|,故∠AOF>45°.由抛物线的对称性可知,∠AOB=∠AOF+∠BOF>45°+45°=90°.
2.(2021·安徽高二期中)在同一平面直角坐标系中,方程9x2+4y2=1与3x+2y2=0的曲线大致为( )
【答案】D
【解析】将方程9x2+4y2=1与3x+2y2=0转化为+=1与y2=-x,所以椭圆的焦点在y轴上,抛物线的焦点在x轴上,且开口向左.故选D.
3.(2021·上海市七宝中学高二月考)已知直线y=kx-k及抛物线y2=2px(p>0),则( )
A.直线与抛物线有一个公共点
B.直线与抛物线有两个公共点
C.直线与抛物线有一个或两个公共点
D.直线与抛物线可能没有公共点
【答案】C
【解析】∵直线y=kx-k=k(x-1),∴直线过定点(1,0).∴当k=0时,直线与抛物线有一个公共点;当k≠0时,直线与抛物线有两个公共点.
4.(2021·浙江省宁波市鄞州中学高二期中)设O为坐标原点,F为抛物线y2=4x的焦点,A为抛物线上一点,若·=-4,则点A的坐标为( )
A.(2,±2 ) B.(1,±2)
C.(1,2) D.(2,2)
【答案】B
【解析】设A(x,y),则y2=4x,①
又=(x,y),=(1-x,-y),
所以·=x-x2-y2=-4.②
由①②可解得x=1,y=±2,故A点坐标为(1,±2).
5.(多选)(2021·郑州一中高二月考)抛物线E:x2=4y与圆M:x2+(y-1)2=16交于A,B两点,圆心M(0,1),点P为劣弧上不同于A,B的一个动点,平行于y轴的直线PN交抛物线于点N,则△PMN的周长的可能取值是( )
A.8 B.8.5 C.9 D.10
【答案】BC
【解析】如图,可得圆心M(0,1)也是抛物线的焦点,
过P作准线的垂线,垂足为H,根据抛物线的定义,可得|MN|=|NH|,
故△PMN的周长l=|NH|+|NP|+|MP|=|PH|+4,由得B(2,3).
|PH|的取值范围为(4,6),∴△PMN的周长|PH|+4的取值范围为(8,10),
故B,C满足条件.
6.(2021·上海华师大二附中高二月考)直线y=x-1被抛物线y2=4x截得的线段的中点坐标是________.
【答案】 (3,2)
【解析】将y=x-1代入y2=4x,整理,得x2-6x+1=0.由根与系数的关系,得x1+x2=6,=3,
∴===2.
∴所求点的坐标为(3,2).
7.(2021·四川省南充高级中学高二月考)已知A(2,0),B为抛物线y2=x上的一点,则|AB|的最小值为________.
【答案】
【解析】设点B(x,y),则x=y2≥0,所以|AB|====.所以当x=时,|AB|取得最小值,且|AB|min=.
8.已知正三角形的一个顶点位于坐标原点,另两个顶点在抛物线y2=2x上,则这个正三角形的边长是 .
【答案】4
【解析】根据抛物线的对称性可知,正三角形另外两个顶点关于x轴对称,设一个顶点坐标为,边长为a,则有tan,解得y0=2,故边长a=4.
9.(2021·天津高二专题练习)设抛物线W:y2=4x的焦点为F,直线l:y=x+m与抛物线W相交于A,B两点,点Q为线段AB的中点.
(1)求m的取值范围;
(2)求证:点Q的纵坐标为定值.
【答案】2
【解析】(1)直线l:y=x+m与抛物线W联立得x2+(2m-4)x+m2=0,
∴Δ=(2m-4)2-4m2>0,解得m<1.
(2)证明:设A(x1,y1),B(x2,y2),则x1+x2=4-2m,x1x2=m2,则点Q的纵坐标为==2.
∴点Q的纵坐标为定值2.
10.(2021·山西太原五中高二月考)抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线的标准方程.
【解析】如图,依题意可设抛物线的标准方程为y2=2px(p>0),
则直线方程为y=-x+p.
设直线交抛物线于A(x1,y1),
B(x2,y2),
过A,B分别作准线的垂线,垂足分别为C,D,则由抛物线定义,得
|AB|=|AF|+|FB|=|AC|+|BD|=x1++x2+,
即x1+x2+p=8.①
又A(x1,y1),B(x2,y2)是直线和抛物线的交点,
由
消去y,得x2-3px+=0.
所以x1+x2=3p,②
将②代入①,得p=2.
所以抛物线的标准方程为y2=4x.
当抛物线方程设为y2=-2px(p>0)时,
同理可求得抛物线标准方程为y2=-4x.
故抛物线的标准方程为y2=4x或y2=-4x.
11.(2021·甘肃省白银高三联考)如图,圆锥底面半径为,体积为,、是底面圆的两条互相垂直的直径,是母线的中点,已知过与的平面与圆锥侧面的交线是以为顶点的抛物线的一部分,则该抛物线的焦点到其准线的距离等于______.
【答案】1
【解析】由,得,则,,,
以为坐标原点,为x轴,与平行的直线为y轴建立如图所示的平面直角坐标系,则,设抛物线的方程为,∴,解得,故焦点到其准线的距离等于.
12.(多选) (2021·上海市杨浦高级中学高二月考)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.△ABF是等边三角形
B.|BF|=3
C.点F到准线的距离为3
D.抛物线C的方程为y2=6x
【答案】ACD
【解析】∵以F为圆心,|FA|为半径的圆交l于B,D两点,∠ABD=90°,由抛物线的定义可得|AB|=|AF|=|BF|,∴△ABF是等边三角形,∴∠FBD=30°.∵△ABF的面积为|BF|2=9,∴|BF|=6.又点F到准线的距离为|BF|sin 30°=3=p,则该抛物线的方程为y2=6x.
13.(2021·安徽马鞍山二中高二开学考试)已知抛物线y2=2x,直线l的方程为x-y+3=0,点P是抛物线上的一动点,则点P到直线l的最短距离为________,此时点P的坐标为________.
【答案】
【解析】设点P(x0,y0)是y2=2x上任意一点,则点P到直线x-y+3=0的距离d===,当y0=1时,dmin==,此时x0=,所以点P的坐标为.
14.(2021·河北沧州市·高二期中)在①,②,③轴时,这三个条件中任选一个,补充在下面的问题中,并回答.
问题:已知抛物线的焦点为,点在抛物线上,且______,
(1)求抛物线的标准方程;
(2)若直线与抛物线交于,两点,求的面积.
【解析】(1)若选①:由抛物线的性质可得
因为,所以,解得.
故抛物线C的标准方程为.
若选②:因为所以,
因为点在抛物线C上,所以,
即,解得,
故抛物线C的标准方程为.
若选③:因为轴,所以,
因为,所以.
故抛物线C的标准方程为.
(2)设由(1)可知.
联立,整理得,
则,
故,
因为点到直线的距离,
所以的面积为.
15.(2021·山东青岛二中高二期中)如果你留心使会发现,汽车前灯后的反射镜呈抛物线的形状,把抛物线沿它的对称轴旋转一周,就会形成一个抛物面.这种抛物面形状,正是我们熟悉的汽车前灯的反射镜形状,这种形状使车灯既能够发出明亮的、照射很远的平行光束,又能发出较暗的,照射近距离的光线.我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成,明亮的光束,是由位于抛物面形状反射镜焦点的光源射出的,灯泡位于抛物面的焦点上,灯泡发出的光经抛物面反射镜反射形成平行光束,再经过配光镜的散射、偏转作用,以达到照亮路面的效果,这样的灯光我们通常称为远光灯:而较暗的光线,不是由反射镜焦点的光源射出的,光线的行进与抛物线的对称轴不平行,光线只能向上和向下照射,所以照射距离并不远,如果把向上射出的光线遮住.车灯就只能发出向下的、射的很近的光线了.请用数学的语言归纳表达远光灯的照明原理,并证明.
【解析】远光灯照明原理:由抛物线的焦点所在的光源发出的光线经抛物线反射后与抛物线的对称轴平行.
证明:不妨设抛物线方程为:y2=2px(p>0),焦点为F,P为抛物线上一点,FP的反射光线为PN,
如图所示:设抛物线过点P的切线为直线l,法线交x轴于M,
由光的反射性质可知∠FPM=∠MPN,
由y2=2px,不妨设P在第一象限,P(,y0),
当y0=0时,直线l与y轴重合,显然PN与x轴重合,
当y0≠0时,设直线l的斜率为k,
则直线l的方程为:y=k(x)+y0,
代入抛物线方程可得:ky2﹣2py﹣ky02+2py0=0,
令△=4p2﹣4k(2py0﹣ky02)=0可得k,
故法线PM的斜率为.
不妨设P在第一象限,设∠PMx=α,∠PFM=β,∠NPM=θ,
则tanα,tanβ,
∴tanθ=tan∠FPM=tan(α﹣β).
∴tanθ+tanα=0,故α+θ=π,
∴PN∥x轴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.3.2抛物线的简单几何性质
要点 抛物线的简单几何性质
标准方程 y2=2px (p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
p的几何意义:焦点F到准线l的距离
图形
顶点 O(0,0)
离心率
对称轴 x轴 y轴
焦点 F F F F
离心率 e=1
准线方程 x=- x= y=- y=
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
开口方向 向右 向左 向上 向下
焦半径(其中P(x0,y0)) |PF|=x0+ |PF|=-x0+ |PF|=y0+ |PF|=-y0+
【方法技巧】
(1)通过上述表格可知,四种形式的抛物线的顶点相同,均为O(0,0),离心率均为1,它们都是轴对称图形,关于焦点所在的坐标轴对称.
(2)抛物线与椭圆、双曲线几何性质的差异:
①抛物线、椭圆和双曲线都是轴对称图形,但椭圆和双曲线又是中心对称图形;
②顶点个数不同,椭圆有4个顶点,双曲线有2个顶点,抛物线只有1个顶点;
③焦点个数不同,椭圆和双曲线各有2个焦点,抛物线只有1个焦点;
④离心率取值范围不同,椭圆的离心率取值范围是0
⑤椭圆和双曲线都有2条准线,而抛物只有1条准线;
⑥椭圆是封闭式曲线,双曲线和抛物线都是非封闭式曲线,由于抛物线没有渐近线,所以在画抛物线时切忌将其画成双曲线的一支的形式.
【答疑解惑】
教材P137
建系如教材P136例5.设抛物线的方程为y2=2px,过焦点的直线方程为my=x-,由消去x,得y2-2pmy-p2=0.
设直线与抛物线的两交点为A(,y1),B(,y2),则由根与系数的关系,得y1y2=-p2.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)抛物线x2=2py(p>0)有一条对称轴为y轴.( )
(2)抛物线y=-x2的准线方程是x=.( )
(3)抛物线是中心对称图形.( )
(4)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线,共可作3条.( )
【答案】(1)√(2)×(3)×(4)√
2.顶点在原点,对称轴为y轴,顶点到准线的距离为4的抛物线方程是( )
A.x2=16y B.x2=8y C.x2=±8y D.x2=±16y
【答案】D
【解析】顶点在原点,对称轴为y轴的抛物线方程有两个:x2=-2py,x2=2py(p>0).由顶点到准线的距离为4知p=8,故所求抛物线方程为x2=16y,x2=-16y.故选D.
3.过抛物线y2=4x的焦点作直线交抛物于A(x1,y1),B(x2,y2)两点,若x1+x2=6,则|AB|=( )
A.10 B.8 C.6 D.4
【答案】B
【解析】|AB|=x1+x2+p=6+2=8.故选B.
4.已知过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,|AF|=2,则|BF|=________.
【答案】2
【解析】F(1,0),由抛物线定义得A点横坐标为1.∴AF⊥x轴,∴|BF|=|AF|=2.
题型一 由抛物线的几何性质求其方程
【例1】已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值、抛物线方程和准线方程.
【解析】解法一:由抛物线开口方向向下,可设抛物线方程为x2=-2py(p>0),则焦点为F.
因为M(m,-3)在抛物线上,且|MF|=5,
所以解得
所以抛物线方程为x2=-8y,m=±2,准线方程为y=2.
解法二:设抛物线方程为x2=-2py(p>0),则焦点为F,准线l:y=,如图所示,作MN⊥l,垂足为N,则|MN|=|MF|=5,而|MN|=3+,所以3+=5,即p=4.
又因为点M在抛物线上,所以m2=24,所以m=±2.
所以抛物线方程为x2=-8y,m=±2,准线方程为y=2.
【方法技巧】
1.代数法:将几何性质转化为坐标表达式,解方程(组)求出未知数.
2.几何法:将几何性质与抛物线定义相结合,采用几何法求出焦准距,从而得到抛物线的标准方程.
【变式训练】
1.边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A,B的抛物线方程是( )
A.y2=x B.y2=-x C.y2=±x D.y2=±x
【答案】C
【解析】设抛物线方程为y2=ax(a≠0).
又A(取点A在x轴上方),
则有=±a,解得a=±,所以抛物线方程为y2=±x.故选C.
2.已知抛物线的顶点在坐标原点,对称轴为x轴且与圆x2+y2=4相交的公共弦长等于2,则抛物线的方程为________.
【答案】(2)y2=3x或y2=-3x
【解析】(2)根据抛物线和圆的对称性知,其交点纵坐标为±,交点横坐标为±1,则抛物线过点(1,)或(-1,),设抛物线方程为
y2=2px或y2=-2px(p>0),
则2p=3,从而抛物线方程为y2=3x或y2=-3x.
题型二 由抛物线的方程研究其几何性质
【例2】已知等边三角形AOB的顶点A,B在抛物线y2=x上,O为坐标原点,顶点A到抛物线的焦点F的距离等于,则△AOB的面积为________.
【答案】3
【解析】∵△AOB是等边三角形,A、B在抛物线y2=x上,∴顶点A,B关于抛物线的对称轴(x轴)对称,
不妨设A(y0,)(y0>0),则B(y0,-).
由|AF|=y0+=,解得y0=3,∴=,
∴△AOB的边长|AB|=2=2,
∴△AOB的面积为×(2)2×=3.
【方法技巧】
把握三个要点,确定抛物线的简单几何性质
1.开口方向:由抛物线标准方程看其开口方向,关键是看准二次项是x还是y,一次项的系数是正还是负.
2.位置关系:顶点位于焦点和准线与坐标轴的交点中间,准线垂直于对称轴.
3.定值:焦点到准线的距离为|p|,过焦点垂直于对称轴的弦(又称为通径)长为2|p|.
【变式训练】
抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=________.
【答案】x2+=1
【解析】设P(x0,y0),Q(x,y),由中点坐标公式得∴又∵点P在椭圆+=1上,∴+=1,即x2+=1.
【答案】6
【解析】如图,在正三角形ABF中,DF=p,BD=p,则B点坐标为.又点B在双曲线上,故-=1.解得p=6.
题型三 直线与抛物线的位置关系
探究1 弦长问题
【例3】已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点.
(1)若|AF|=4,求点A的坐标;
(2)求线段AB的长的最小值.
【解析】由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).设A(x1,y1),B(x2,y2).
(1)由抛物线的定义可知,|AF|=x1+,从而x1=4-1=3.代入y2=4x,解得y1=±2.
∴点A的坐标为(3,2)或(3,-2).
(2)当直线l的斜率存在时,
设直线l的方程为y=k(x-1).
与抛物线方程联立,得
消去y,整理得k2x2-(2k2+4)x+k2=0.
∵直线与抛物线相交于A,B两点,
则k≠0,并设其两根为x1,x2,∴x1+x2=2+.
由抛物线的定义可知,|AB|=x1+x2+p=4+>4.
当直线l的斜率不存在时,直线l的方程为x=1,与抛物线相交于A(1,2),B(1,-2),此时|AB|=4,
∴|AB|≥4,即线段AB的长的最小值为4.
【方法技巧】
抛物线弦长的求解思路
1.当直线的斜率k存在且k≠0时,弦长公式为|AB|=|x1-x2|=|y1-y2|;当直线的斜率k=0时,只有抛物线的对称轴是y轴时弦长存在,弦长公式为|AB|=|x1-x2|;当直线的斜率k不存在时,只有抛物线的对称轴是x轴时弦长存在,弦长公式为|AB|=|y1-y2|.
2.焦点弦是特殊的弦,除了可以利用以上方法求解,还可以利用抛物线的定义转化为焦半径和焦点弦长问题处理.注意熟记抛物线的四种标准方程对应的焦点弦长公式.
探究2 中点弦问题
【例4】已知抛物线y2=2x,过点Q(2,1)作一条直线交抛物线于A,B两点,试求弦AB的中点的轨迹方程.
【分析】方法一:利用点差法,设点作差,要考虑斜率不存在的情况;
方法二:可设出斜率存在时的直线的方程,将其与抛物线方程联立,可得一元二次方程,利用根与系数的关系及中点坐标公式,消参即可得轨迹方程,同时要考虑斜率不存在的情况.
【解析】方法一 设A(x1,y1),B(x2,y2),弦AB的中点为M(x,y),则y1+y2=2y,当直线AB的斜率存在时,kAB==.
易知
①-②,得(y1+y2)(y1-y2)=2(x1-x2),
所以2y·=2,即2y·=2,即2=x-(y≠0).
当直线AB的斜率不存在,即AB⊥x轴时,AB的中点为(2,0),适合上式,故所求轨迹方程为2=x-.
方法二 当直线AB的斜率存在时,设直线AB的方程为y-1=k(x-2)(k≠0),由得y2-y+1-2k=0.则所以k∈(-∞,0)∪(0,+∞).
设A(x1,y1),B(x2,y2),AB的中点为P(x,y),则y1+y2=,y1y2=.
所以x1+x2=(y+y)=[(y1+y2)2-2y1y2]==.
则x==,y==,
消去k得2=x-(y≠0).
当直线AB的斜率不存在,即AB⊥x轴时,AB的中点为(2,0),适合上式.
故所求轨迹方程为2=x-.
【方法技巧】
(1)方法一中得到kAB的等式是为点差法做准备.
(2)方法一中因为用点差法求轨迹方程时用到了斜率,所以必须验证斜率不存在的情况.
(3)方法二中直线与抛物线相交于两点,隐含着条件Δ>0.
(4)方法二中求y1+y2及x1+x2是为利用中点坐标公式做准备.
【方法技巧】
解决中点弦问题的思路
解决中点弦问题的基本方法是点差法、利用根与系数的关系,直线与抛物线的方程联立时消y有时更简捷,此类问题还要注意斜率不存在的情况,避免漏解.一般地,已知抛物线y2=2px(p>0)上两点A(x1,y1),B(x2,y2)及AB的中点P(x0,y0),则kAB=.
直线AB的方程为y-y0=(x-x0).
线段AB的垂直平分线的方程为y-y0=-(x-x0).
【变式训练】
1.斜率为的直线经过抛物线x2=8y的焦点,且与抛物线相交于A,B两点,则线段AB的长为________.
【答案】10
【解析】(1)方法一 由题意设A(x1,y1),B(x2,y2),则对于抛物线x2=8y,焦点弦长|AB|=p+y1+y2=4+y1+y2.
因为抛物线x2=8y的焦点为(0,2),且直线AB的斜率为,所以直线AB的方程为y=x+2,代入抛物线方程x2=8y,消去x整理得y2-6y+4=0,从而y1+y2=6,所以|AB|=10.
故线段AB的长为10.
方法二 由题意设A(x1,y1),B(x2,y2).由题意得抛物线的焦点为(0,2),故直线AB的方程为y=x+2,即x-2y+4=0,
由消去y得x2-4x-16=0,
则x1+x2=4,x1x2=-16,代入弦长公式|AB|=,得|AB|=10.
2.已知斜率为k的直线l与抛物线C:y2=4x交于A、B两点,线段AB的中点为M(2,1),则直线l的方程为( )
A.2x-y-3=0 B.2x-y-5=0 C.x-2y=0 D.x-y-1=0
【答案】A
【解析】设A(x1,y1),B(x2,y2),则 ==2,所以k=2,因为直线过点M(2,1),所以直线l的方程为2x-y-3=0.故选A.
易错辨析 忽略直线与抛物线有一个公共点的特殊情况致误
【例5】(多选)过定点P(-1,1)且与抛物线y2=2x只有一个交点的直线l的方程为( )
A.y=-1 B.y=1 C.(-1)x-2y++1=0 D.(1+)x+2y+-1=0
【答案】BCD
【解析】(1)当直线l的斜率不存在时,显然不满足题意.
(2)当直线l的斜率存在时,
①若直线l与抛物线的对称轴平行,则直线l的方程为y=1,此时直线l与抛物线只有一个公共点.
②若直线l与抛物线的对称轴不平行,设直线l的方程为y-1=k(x+1)(k≠0)
即y=k(x+1)+1(k≠0)
由消去x,得ky2-2y+2k+2=0
由题意知Δ=4-4k(2k+2)=0,解得k=
故所求直线l的方程为:
(-1)x-2y++1=0或(1+)x+2y+-1=0
综上所述,所求直线l的方程为y=1或(-1)x-2y++1=0或(1+)x+2y+-1=0.故选BCD.
【易错提醒】
易错原因 纠错心得
本题易错的地方是只考虑直线l的斜率k存在且不为0时的情形,而忽略k不存在及直线l平行于抛物线的对称轴这两种情形. 在涉及直线与抛物线只有一个交点的问题时,应提防两处陷阱:一是直线与对称轴平行时,直线与抛物线只有一个交点,这是由Δ=0无法得到的(事实上,此时消元后对应的“一元二次”方程的“二次”项系数一定为零);二是若由Δ=0仅得到一条直线,则意味着斜率不存在的直线可能与抛物线相切(仅有一个交点),应检验斜率不存在的直线是否满足条件.
1.过抛物线y2=2px(p>0)的焦点,且垂直于x轴的弦为AB,O为抛物线的顶点,则∠AOB的度数( )
A.小于90° B.等于90°
C.大于90° D.不能确定
【答案】C
【解析】设抛物线y2=2px的焦点为F,则其坐标为,将x=代入抛物线的方程,解得A,B.在直角三角形AOF中,|OF|<|AF|,故∠AOF>45°.由抛物线的对称性可知,∠AOB=∠AOF+∠BOF>45°+45°=90°.
2.(2021·安徽高二期中)在同一平面直角坐标系中,方程9x2+4y2=1与3x+2y2=0的曲线大致为( )
【答案】D
【解析】将方程9x2+4y2=1与3x+2y2=0转化为+=1与y2=-x,所以椭圆的焦点在y轴上,抛物线的焦点在x轴上,且开口向左.故选D.
3.(2021·上海市七宝中学高二月考)已知直线y=kx-k及抛物线y2=2px(p>0),则( )
A.直线与抛物线有一个公共点
B.直线与抛物线有两个公共点
C.直线与抛物线有一个或两个公共点
D.直线与抛物线可能没有公共点
【答案】C
【解析】∵直线y=kx-k=k(x-1),∴直线过定点(1,0).∴当k=0时,直线与抛物线有一个公共点;当k≠0时,直线与抛物线有两个公共点.
4.(2021·浙江省宁波市鄞州中学高二期中)设O为坐标原点,F为抛物线y2=4x的焦点,A为抛物线上一点,若·=-4,则点A的坐标为( )
A.(2,±2 ) B.(1,±2)
C.(1,2) D.(2,2)
【答案】B
【解析】设A(x,y),则y2=4x,①
又=(x,y),=(1-x,-y),
所以·=x-x2-y2=-4.②
由①②可解得x=1,y=±2,故A点坐标为(1,±2).
5.(多选)(2021·郑州一中高二月考)抛物线E:x2=4y与圆M:x2+(y-1)2=16交于A,B两点,圆心M(0,1),点P为劣弧上不同于A,B的一个动点,平行于y轴的直线PN交抛物线于点N,则△PMN的周长的可能取值是( )
A.8 B.8.5 C.9 D.10
【答案】BC
【解析】如图,可得圆心M(0,1)也是抛物线的焦点,
过P作准线的垂线,垂足为H,根据抛物线的定义,可得|MN|=|NH|,
故△PMN的周长l=|NH|+|NP|+|MP|=|PH|+4,由得B(2,3).
|PH|的取值范围为(4,6),∴△PMN的周长|PH|+4的取值范围为(8,10),
故B,C满足条件.
6.(2021·上海华师大二附中高二月考)直线y=x-1被抛物线y2=4x截得的线段的中点坐标是________.
【答案】 (3,2)
【解析】将y=x-1代入y2=4x,整理,得x2-6x+1=0.由根与系数的关系,得x1+x2=6,=3,
∴===2.
∴所求点的坐标为(3,2).
7.(2021·四川省南充高级中学高二月考)已知A(2,0),B为抛物线y2=x上的一点,则|AB|的最小值为________.
【答案】
【解析】设点B(x,y),则x=y2≥0,所以|AB|====.所以当x=时,|AB|取得最小值,且|AB|min=.
8.已知正三角形的一个顶点位于坐标原点,另两个顶点在抛物线y2=2x上,则这个正三角形的边长是 .
【答案】4
【解析】根据抛物线的对称性可知,正三角形另外两个顶点关于x轴对称,设一个顶点坐标为,边长为a,则有tan,解得y0=2,故边长a=4.
9.(2021·天津高二专题练习)设抛物线W:y2=4x的焦点为F,直线l:y=x+m与抛物线W相交于A,B两点,点Q为线段AB的中点.
(1)求m的取值范围;
(2)求证:点Q的纵坐标为定值.
【答案】2
【解析】(1)直线l:y=x+m与抛物线W联立得x2+(2m-4)x+m2=0,
∴Δ=(2m-4)2-4m2>0,解得m<1.
(2)证明:设A(x1,y1),B(x2,y2),则x1+x2=4-2m,x1x2=m2,则点Q的纵坐标为==2.
∴点Q的纵坐标为定值2.
10.(2021·山西太原五中高二月考)抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线的标准方程.
【解析】如图,依题意可设抛物线的标准方程为y2=2px(p>0),
则直线方程为y=-x+p.
设直线交抛物线于A(x1,y1),
B(x2,y2),
过A,B分别作准线的垂线,垂足分别为C,D,则由抛物线定义,得
|AB|=|AF|+|FB|=|AC|+|BD|=x1++x2+,
即x1+x2+p=8.①
又A(x1,y1),B(x2,y2)是直线和抛物线的交点,
由
消去y,得x2-3px+=0.
所以x1+x2=3p,②
将②代入①,得p=2.
所以抛物线的标准方程为y2=4x.
当抛物线方程设为y2=-2px(p>0)时,
同理可求得抛物线标准方程为y2=-4x.
故抛物线的标准方程为y2=4x或y2=-4x.
11.(2021·甘肃省白银高三联考)如图,圆锥底面半径为,体积为,、是底面圆的两条互相垂直的直径,是母线的中点,已知过与的平面与圆锥侧面的交线是以为顶点的抛物线的一部分,则该抛物线的焦点到其准线的距离等于______.
【答案】1
【解析】由,得,则,,,
以为坐标原点,为x轴,与平行的直线为y轴建立如图所示的平面直角坐标系,则,设抛物线的方程为,∴,解得,故焦点到其准线的距离等于.
12.(多选) (2021·上海市杨浦高级中学高二月考)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.△ABF是等边三角形
B.|BF|=3
C.点F到准线的距离为3
D.抛物线C的方程为y2=6x
【答案】ACD
【解析】∵以F为圆心,|FA|为半径的圆交l于B,D两点,∠ABD=90°,由抛物线的定义可得|AB|=|AF|=|BF|,∴△ABF是等边三角形,∴∠FBD=30°.∵△ABF的面积为|BF|2=9,∴|BF|=6.又点F到准线的距离为|BF|sin 30°=3=p,则该抛物线的方程为y2=6x.
13.(2021·安徽马鞍山二中高二开学考试)已知抛物线y2=2x,直线l的方程为x-y+3=0,点P是抛物线上的一动点,则点P到直线l的最短距离为________,此时点P的坐标为________.
【答案】
【解析】设点P(x0,y0)是y2=2x上任意一点,则点P到直线x-y+3=0的距离d===,当y0=1时,dmin==,此时x0=,所以点P的坐标为.
14.(2021·河北沧州市·高二期中)在①,②,③轴时,这三个条件中任选一个,补充在下面的问题中,并回答.
问题:已知抛物线的焦点为,点在抛物线上,且______,
(1)求抛物线的标准方程;
(2)若直线与抛物线交于,两点,求的面积.
【解析】(1)若选①:由抛物线的性质可得
因为,所以,解得.
故抛物线C的标准方程为.
若选②:因为所以,
因为点在抛物线C上,所以,
即,解得,
故抛物线C的标准方程为.
若选③:因为轴,所以,
因为,所以.
故抛物线C的标准方程为.
(2)设由(1)可知.
联立,整理得,
则,
故,
因为点到直线的距离,
所以的面积为.
15.(2021·山东青岛二中高二期中)如果你留心使会发现,汽车前灯后的反射镜呈抛物线的形状,把抛物线沿它的对称轴旋转一周,就会形成一个抛物面.这种抛物面形状,正是我们熟悉的汽车前灯的反射镜形状,这种形状使车灯既能够发出明亮的、照射很远的平行光束,又能发出较暗的,照射近距离的光线.我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成,明亮的光束,是由位于抛物面形状反射镜焦点的光源射出的,灯泡位于抛物面的焦点上,灯泡发出的光经抛物面反射镜反射形成平行光束,再经过配光镜的散射、偏转作用,以达到照亮路面的效果,这样的灯光我们通常称为远光灯:而较暗的光线,不是由反射镜焦点的光源射出的,光线的行进与抛物线的对称轴不平行,光线只能向上和向下照射,所以照射距离并不远,如果把向上射出的光线遮住.车灯就只能发出向下的、射的很近的光线了.请用数学的语言归纳表达远光灯的照明原理,并证明.
【解析】远光灯照明原理:由抛物线的焦点所在的光源发出的光线经抛物线反射后与抛物线的对称轴平行.
证明:不妨设抛物线方程为:y2=2px(p>0),焦点为F,P为抛物线上一点,FP的反射光线为PN,
如图所示:设抛物线过点P的切线为直线l,法线交x轴于M,
由光的反射性质可知∠FPM=∠MPN,
由y2=2px,不妨设P在第一象限,P(,y0),
当y0=0时,直线l与y轴重合,显然PN与x轴重合,
当y0≠0时,设直线l的斜率为k,
则直线l的方程为:y=k(x)+y0,
代入抛物线方程可得:ky2﹣2py﹣ky02+2py0=0,
令△=4p2﹣4k(2py0﹣ky02)=0可得k,
故法线PM的斜率为.
不妨设P在第一象限,设∠PMx=α,∠PFM=β,∠NPM=θ,
则tanα,tanβ,
∴tanθ=tan∠FPM=tan(α﹣β).
∴tanθ+tanα=0,故α+θ=π,
∴PN∥x轴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
