2021-2022学年人教版八年级上册数学14.1.2幂的乘方课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学14.1.2幂的乘方课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 09:45:19 | ||
图片预览





文档简介
(共19张PPT)
14.1.2幂的乘方
八年级上册 RJ
学习目标
学习重点
1.根据乘方的意义和同底数幂的乘法探究出幂的
乘方法则,培养学生思维的灵活性。
2.灵活运用幂的乘方进行计算。
学习难点
理解幂的乘方法则推导过程,区分幂的乘方和同底数幂的乘法。
灵活运用幂的乘方进行计算。
课前热身
1.根据上节所学的同底数幂的乘法的内容,完成下列填空
(1)同底数幂的乘法:
am·an= (m、n都是正整数)
同底数幂相乘,底数________,指数_______。
(2)73×75= _______ a6·a2= ________
x2·x3·x4= ______ (-x)3·(-x)5= ________
教学导入
一
amn
不变
78
a8
X9
x8
相乘
新课导入
教学导入
一
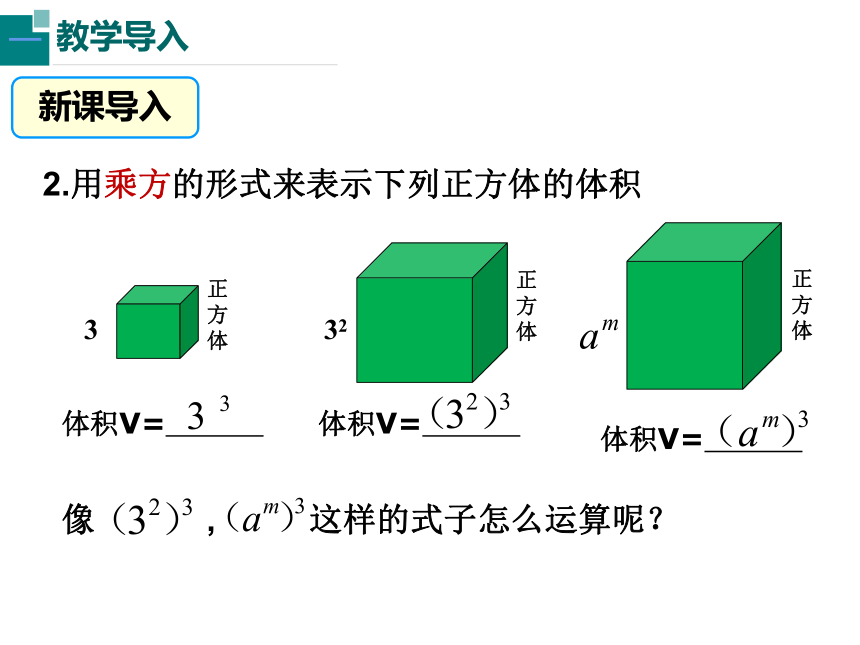
32
体积V=
体积V=
正方体
正方体
2.用乘方的形式来表示下列正方体的体积
3
正方体
体积V=
像 , 这样的式子怎么运算呢?
问题1
根据乘方的意义及同底数幂的乘法填空.
(1) (32)3 =( ) ×( ) ×( )=_________=3( )
(2)(a2)3 =( ) ×( ) ×( ) =_________= a( )
(3) (am)3 =( ) ×( ) ×( )=_________= a( ).
(m为正整数)
问题2:观察上面的计算结果,你能发现什么规律?
能不能用式子将你的发现表示出来?
问题3: 猜想:(am )n =_______,(m,n为正整数)
并验证猜想
第一学程
一
问题2
问题3
自学要求:3min
独立计算思考
互学要求:2min
(1)有序交流。组长主持,组内交流,及时指导。
(2)汇总意见。
(3)展学准备。组长分工,做好展讲准备。
展学要求:
(1)普通话, 声音洪亮,语言流畅,分工合理,解题方法得当,
(2)其他小组认真倾听, 准备补充、质疑提问,对展示小组进行
评价
问题1
根据乘方的意义及同底数幂的乘法填空.
(1) (32)3 =( ) ×( ) ×( )=_________=3( )
(2)(a2)3 =( ) ×( ) ×( ) =_________= a( )
(3) (am)3 =( ) ×( ) ×( )=_________= a( ).
(m为正整数)
问题2:观察上面的计算结果,你能发现什么规律?
能不能用式子将你的发现表示出来?
问题3: 猜想:(am )n =_______,(m,n为正整数)
并验证猜想
第一学程
一
问题2
问题3
32
32
32
32+2+2
a2
a2
a2
a2+2+2
am
am
am
am+m+m
6
6
3m
第一学程
一
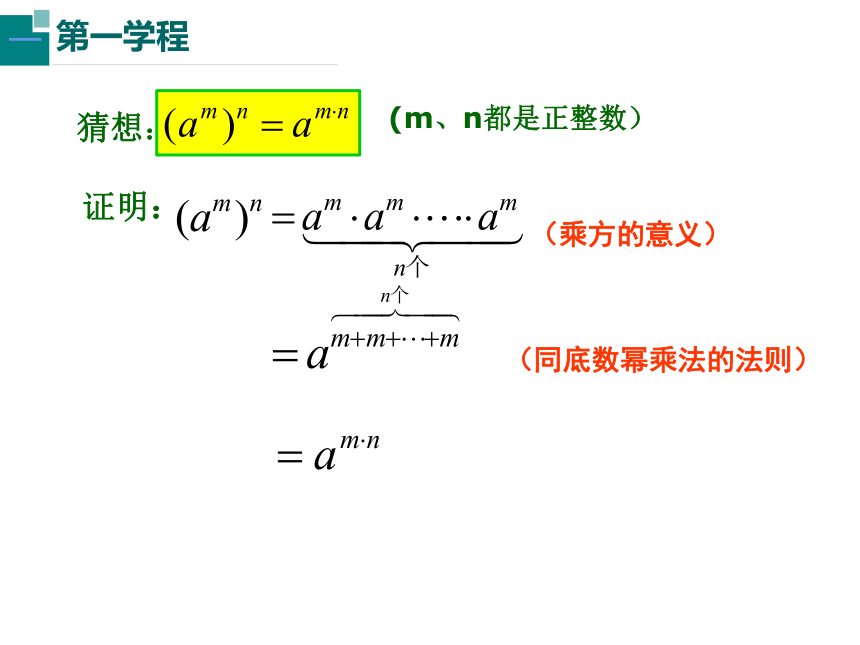
猜想:
(m、n都是正整数)
证明:
(乘方的意义)
(同底数幂乘法的法则)
第一学程
一
幂的乘方的运算法则:
(m、n都是正整数)
幂的乘方,底数不变,指数相乘 。
如:
[(32)3]5=
(36)5=
公式推广
(m、n、p都是正整数)
330
第二学程
一
问题1
趁热打铁 计算下列各题
(1) (85)3= (2) (a4)4=
(3) (am)2= (4) -(x4)3=
(5) (y3)2·y= (6) 2(a2)6-(a4)3=
问题2
比较幂的乘方和同底数幂的乘法,完善表格
运算种类 公式 乘法/乘方 运算结果 底数 指数
同底数幂的乘法
幂的乘方
第二学程
一
问题1
趁热打铁 计算下列各题
(1) (85)3= (2) (a4)4=
(3) (am)2= (4) -(x4)3=
(5) (y3)2·y=
(6) 2(a2)6-(a4)3
85×3=815
a4×4=a16
a2m
=2a2×6-a4×3
=2a12-a12 同类项
=2·a12-1·a12
=(2-1)a12 乘法分配律合并同类项
=a12
y3×2·y=y6·y=y6+1=y7
-(X4×3)=-X12
第二学程
一
问题2
比较幂的乘方和同底数幂的乘法,完善表格
运算种类 公式 乘法/乘方 运算结果 底数 指数
同底数幂的乘法
幂的乘方
am·an=am+n
(am)n=amn
m,n均为正整数
乘法
乘方
不变
不变
相乘
相加
第二学程
一
问题3
幂的乘方的逆用
amn=( )n= ( )m (m,n为正整数)
若9×27n=34n+1求n的值
解:∵ 9×27n
=32 ×(33)n
=32 ×33n
=32+3n
=34n+1
∴ 2+3n=4n+1
∴ n=1
am
an
第三学程 当堂达标
一
1.计算:
(1)(-b5)5= (2)-(x2)m=
(3)(an-2)3= (4)[(x-y)3]2·[(x-y)2]3=
2.判断正误,说明理由
(1)(a4)3=a7 (2) a4·a3=a12
(3) (a2)3+(a3)2=a12 (4) (-x3)2=(-x2)3
3.已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
第三学程 当堂达标
一
1.计算:
(1)(-b5)5=
(2)-(x2)m=
(3)(an-2)3=
(4)[(x-y)3]2·[(y-x)2]3=
2.判断正误,错误的请改正
(1)(a4)3=a7 (2) a4·a3=a12
(3) (a2)3+(a3)2=a12 (4) (-x3)2=(-x2)3
-b5×5=-b25
-X2m
a3(n-2)=a3n-6
(x-y)6·(y-x)6=(x-y)6·(x-y)6=(x-y)12
a12
a7
=a6+a6=2a6
左=X6
右=-X6
第三学程 当堂达标
一
3.已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
解:(1)103m=(10m)3
(2)102n=(10n)2
(3)103m+2n=103m×102n
=(10m)3×(10n)2
=33×22=27×4=108
=33=27
=22=4
课堂小结
一
幂的乘方
法则
(am)n=amn (m,n都是正整数)
注意
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n=amn; am﹒an=am+n
幂的乘方法则的逆用:
amn=(am)n=(an)m
作业布置
一
均衡作业餐——基础知识型
1.计算
(a2)7= (-m3)2 = (a4)4 = (105)6=
2.下列各式中,计算正确的是( )
A.m5·m5=m10 B.(m4)4=m8
C.m3·m3=m9 D.m6+m6=2m12
营养作业餐——应用提升型
3.计算
(1)[(x+y)2]3= (2)-(xm+1) 2= (3)2(a3) 3·(a3) 2=
特色作业餐——拓展提升型
选做题:幂的乘方的逆运算
4.(1)26= ( )2= ( )3 a6= ( )2= ( )3 amn= ( )m= ( )n
(2)若 am= 2,an= 3,求 am+n和 a2m+n的值。
注意:均衡作业餐、营养作业餐、特色作业餐请同学们根据自己的学习能力自主选择。
1.(1)已知x2n=3,求(x3n)4的值;
(2)已知2x+5y-3=0,求4x·32y的值.
拓展提升
一
2. 比较3500,4400,5300的大小.
解析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
解:3500=(35)100=243100,
4400=(44)100=256100,
5300=(53)100=125100.
∵256100>243100>125100,
∴4400>3500>5300.
方法总结:比较底数大于1的幂的大小的方法有两种:(1)底数相同,指数越大,幂就越大;(2)指数相同,底数越大,幂就越大.故在此类题中,一般先观察题目所给数据的特点,将其转化为同底数的幂或同指数的幂,然后再进行大小比较.
拓展提升
一
14.1.2幂的乘方
八年级上册 RJ
学习目标
学习重点
1.根据乘方的意义和同底数幂的乘法探究出幂的
乘方法则,培养学生思维的灵活性。
2.灵活运用幂的乘方进行计算。
学习难点
理解幂的乘方法则推导过程,区分幂的乘方和同底数幂的乘法。
灵活运用幂的乘方进行计算。
课前热身
1.根据上节所学的同底数幂的乘法的内容,完成下列填空
(1)同底数幂的乘法:
am·an= (m、n都是正整数)
同底数幂相乘,底数________,指数_______。
(2)73×75= _______ a6·a2= ________
x2·x3·x4= ______ (-x)3·(-x)5= ________
教学导入
一
amn
不变
78
a8
X9
x8
相乘
新课导入
教学导入
一
32
体积V=
体积V=
正方体
正方体
2.用乘方的形式来表示下列正方体的体积
3
正方体
体积V=
像 , 这样的式子怎么运算呢?
问题1
根据乘方的意义及同底数幂的乘法填空.
(1) (32)3 =( ) ×( ) ×( )=_________=3( )
(2)(a2)3 =( ) ×( ) ×( ) =_________= a( )
(3) (am)3 =( ) ×( ) ×( )=_________= a( ).
(m为正整数)
问题2:观察上面的计算结果,你能发现什么规律?
能不能用式子将你的发现表示出来?
问题3: 猜想:(am )n =_______,(m,n为正整数)
并验证猜想
第一学程
一
问题2
问题3
自学要求:3min
独立计算思考
互学要求:2min
(1)有序交流。组长主持,组内交流,及时指导。
(2)汇总意见。
(3)展学准备。组长分工,做好展讲准备。
展学要求:
(1)普通话, 声音洪亮,语言流畅,分工合理,解题方法得当,
(2)其他小组认真倾听, 准备补充、质疑提问,对展示小组进行
评价
问题1
根据乘方的意义及同底数幂的乘法填空.
(1) (32)3 =( ) ×( ) ×( )=_________=3( )
(2)(a2)3 =( ) ×( ) ×( ) =_________= a( )
(3) (am)3 =( ) ×( ) ×( )=_________= a( ).
(m为正整数)
问题2:观察上面的计算结果,你能发现什么规律?
能不能用式子将你的发现表示出来?
问题3: 猜想:(am )n =_______,(m,n为正整数)
并验证猜想
第一学程
一
问题2
问题3
32
32
32
32+2+2
a2
a2
a2
a2+2+2
am
am
am
am+m+m
6
6
3m
第一学程
一
猜想:
(m、n都是正整数)
证明:
(乘方的意义)
(同底数幂乘法的法则)
第一学程
一
幂的乘方的运算法则:
(m、n都是正整数)
幂的乘方,底数不变,指数相乘 。
如:
[(32)3]5=
(36)5=
公式推广
(m、n、p都是正整数)
330
第二学程
一
问题1
趁热打铁 计算下列各题
(1) (85)3= (2) (a4)4=
(3) (am)2= (4) -(x4)3=
(5) (y3)2·y= (6) 2(a2)6-(a4)3=
问题2
比较幂的乘方和同底数幂的乘法,完善表格
运算种类 公式 乘法/乘方 运算结果 底数 指数
同底数幂的乘法
幂的乘方
第二学程
一
问题1
趁热打铁 计算下列各题
(1) (85)3= (2) (a4)4=
(3) (am)2= (4) -(x4)3=
(5) (y3)2·y=
(6) 2(a2)6-(a4)3
85×3=815
a4×4=a16
a2m
=2a2×6-a4×3
=2a12-a12 同类项
=2·a12-1·a12
=(2-1)a12 乘法分配律合并同类项
=a12
y3×2·y=y6·y=y6+1=y7
-(X4×3)=-X12
第二学程
一
问题2
比较幂的乘方和同底数幂的乘法,完善表格
运算种类 公式 乘法/乘方 运算结果 底数 指数
同底数幂的乘法
幂的乘方
am·an=am+n
(am)n=amn
m,n均为正整数
乘法
乘方
不变
不变
相乘
相加
第二学程
一
问题3
幂的乘方的逆用
amn=( )n= ( )m (m,n为正整数)
若9×27n=34n+1求n的值
解:∵ 9×27n
=32 ×(33)n
=32 ×33n
=32+3n
=34n+1
∴ 2+3n=4n+1
∴ n=1
am
an
第三学程 当堂达标
一
1.计算:
(1)(-b5)5= (2)-(x2)m=
(3)(an-2)3= (4)[(x-y)3]2·[(x-y)2]3=
2.判断正误,说明理由
(1)(a4)3=a7 (2) a4·a3=a12
(3) (a2)3+(a3)2=a12 (4) (-x3)2=(-x2)3
3.已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
第三学程 当堂达标
一
1.计算:
(1)(-b5)5=
(2)-(x2)m=
(3)(an-2)3=
(4)[(x-y)3]2·[(y-x)2]3=
2.判断正误,错误的请改正
(1)(a4)3=a7 (2) a4·a3=a12
(3) (a2)3+(a3)2=a12 (4) (-x3)2=(-x2)3
-b5×5=-b25
-X2m
a3(n-2)=a3n-6
(x-y)6·(y-x)6=(x-y)6·(x-y)6=(x-y)12
a12
a7
=a6+a6=2a6
左=X6
右=-X6
第三学程 当堂达标
一
3.已知10m=3,10n=2,求下列各式的值.
(1)103m;(2)102n;(3)103m+2n.
解:(1)103m=(10m)3
(2)102n=(10n)2
(3)103m+2n=103m×102n
=(10m)3×(10n)2
=33×22=27×4=108
=33=27
=22=4
课堂小结
一
幂的乘方
法则
(am)n=amn (m,n都是正整数)
注意
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n=amn; am﹒an=am+n
幂的乘方法则的逆用:
amn=(am)n=(an)m
作业布置
一
均衡作业餐——基础知识型
1.计算
(a2)7= (-m3)2 = (a4)4 = (105)6=
2.下列各式中,计算正确的是( )
A.m5·m5=m10 B.(m4)4=m8
C.m3·m3=m9 D.m6+m6=2m12
营养作业餐——应用提升型
3.计算
(1)[(x+y)2]3= (2)-(xm+1) 2= (3)2(a3) 3·(a3) 2=
特色作业餐——拓展提升型
选做题:幂的乘方的逆运算
4.(1)26= ( )2= ( )3 a6= ( )2= ( )3 amn= ( )m= ( )n
(2)若 am= 2,an= 3,求 am+n和 a2m+n的值。
注意:均衡作业餐、营养作业餐、特色作业餐请同学们根据自己的学习能力自主选择。
1.(1)已知x2n=3,求(x3n)4的值;
(2)已知2x+5y-3=0,求4x·32y的值.
拓展提升
一
2. 比较3500,4400,5300的大小.
解析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
解:3500=(35)100=243100,
4400=(44)100=256100,
5300=(53)100=125100.
∵256100>243100>125100,
∴4400>3500>5300.
方法总结:比较底数大于1的幂的大小的方法有两种:(1)底数相同,指数越大,幂就越大;(2)指数相同,底数越大,幂就越大.故在此类题中,一般先观察题目所给数据的特点,将其转化为同底数的幂或同指数的幂,然后再进行大小比较.
拓展提升
一
