2021-2022学年数学人教A版(2019)选择性必修第一册3.1椭圆 专题讲义
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册3.1椭圆 专题讲义 |
|
|
| 格式 | docx | ||
| 文件大小 | 463.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览





文档简介
椭 圆
知识梳理
知识点 椭圆的定义
椭圆的定义:
我们把平面内与两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点;
两个焦点之间的距离叫做椭圆的焦距。
知识点 椭圆的方程
1、椭圆的标准方程
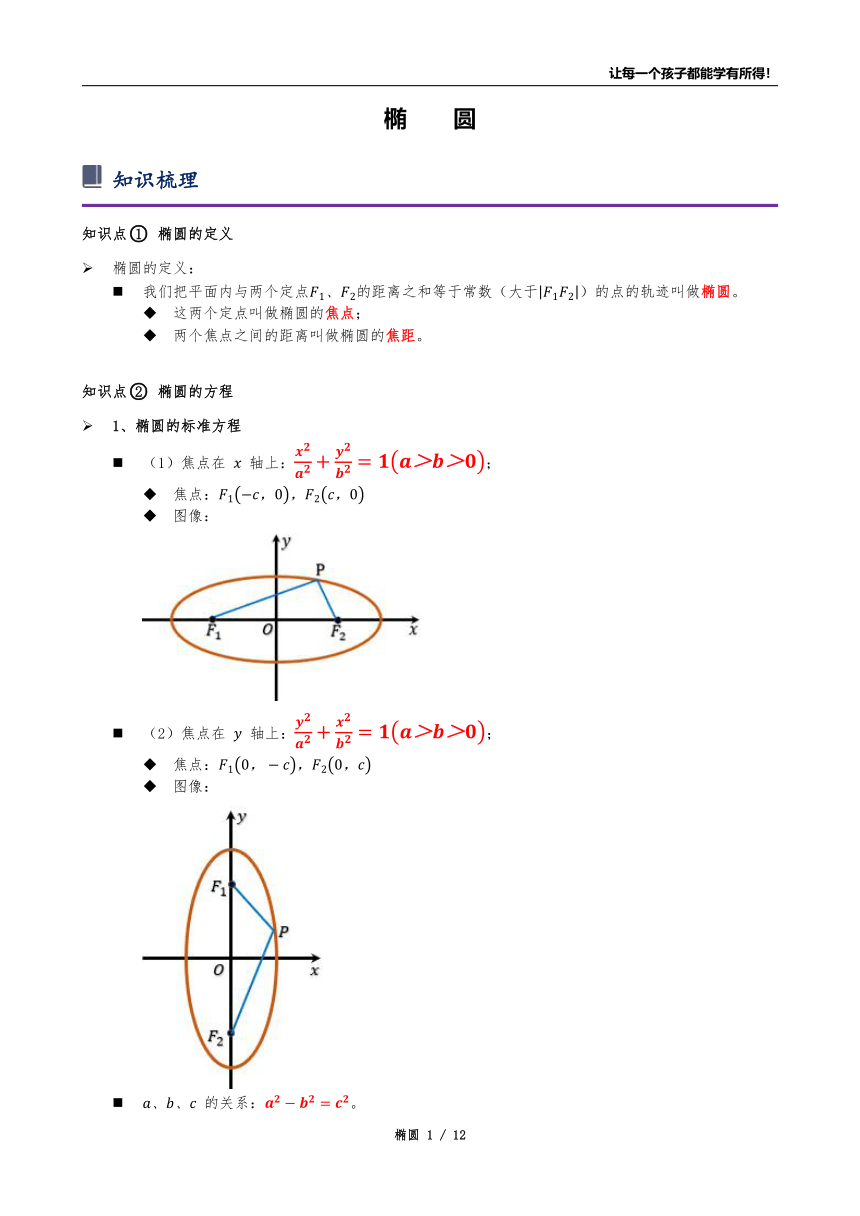
(1)焦点在 轴上:;
焦点:
图像:
(2)焦点在 轴上:;
焦点:
图像:
的关系:。
2、椭圆的一般方程
一般方程:。
充要条件:(同时满足以下三个条件,才能表示椭圆)
(1),
(2)同号,
(3)
3、共焦点的椭圆系方程
(1)与椭圆 有公共焦点的椭圆方程为:
(2)与椭圆 有公共焦点的椭圆方程为:
3、相同离心率的椭圆系方程
(1)与椭圆 有相同离心率的椭圆方程为:
(2)与椭圆 有相同离心率的椭圆方程为:
知识点 椭圆的几何性质
标准方程
范围
对称性 关于 轴、 轴对称,关于原点中心对称
顶点坐标
半轴长 长半轴长为 ,短半轴长为 ,
离心率
知识点 椭圆的离心率
椭圆的焦距与长轴长的比叫做椭圆的离心率,用 表示。即:。
离心率的取值范围:;
离心率对椭圆形状的影响:
(1) 越接近1, 就越接近 ,从而 就越小,椭圆就越扁;
(2) 越接近0, 就越接近 0,从而 就越接近 ,椭圆就越圆。
与 的关系:
知识点 椭圆的通径及有关最值
通径:过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆的通径
长度为:
最值
(1)椭圆上到中心距离最小的点是短轴的两个端点,到中心距离最大的点是长轴的两个端点
(2)椭圆上到焦点距离最大和最小的点是长轴的两个端点,距离的最大值为 ,距离最小值为
(3)对于椭圆上的点P,随着点P从长轴端点向短轴端点移动而逐渐变大,当点P在短轴端点处时,最大
(4)
(5)
知识点 关于椭圆的几个重要结论
1、弦长公式
设直线与椭圆交于两点,则:
2、焦点三角形
P为椭圆上异于长轴端点的点,则称作焦点三角形
若,则的面积:
3、椭圆的切线
椭圆 上一点 处的切线方程为
4、点与椭圆的位置关系:对于椭圆 ,我们有:
(1)在椭圆内部
(2)在椭圆外部
(3)在椭圆上
5、椭圆中斜率乘积为定值的问题
(1)椭圆 长轴的两个端点与椭圆上除这两个顶点外的任一点连线的斜率之积为
(2)设A、B是椭圆 上关于原点对称的两点,点P为该椭圆上不同于A、B的任一点,若直线PA、PB的斜率分别为,则
典型例题
题型 求椭圆的标准方程
1、定义法:验证动点到两定点的距离之和是否等于一个常数,并且该常数大于两定点之间的距离,若符合,则动点的轨迹是一个椭圆。(要注意检验);
2、待定系数法
定位置:确定焦点在哪条坐标轴上
设方程:根据焦点的位置设方程
焦点位置不确定时,分情况讨论,或者设为
寻关系:根据条件列出关于的方程组
得方程:解方程组,得到椭圆方程
例 (1)已知点,点P是圆的任意一点,线段PA的垂直平分线与直线CP交于点E。求点E的轨迹方程。
(2)求经过和两点的椭圆的标准方程。
变式训练:
已知平面内两定点,动点满足。
(1)求动点的轨迹的方程;
(2)若直线与曲线C交于不同的两点、,求。
题型 椭圆中的最值问题
1、利用求函数最值的方法求最值
将问题转化为函数的最值问题处理时,要注意 自身的取值范围,常常化为闭区间上的二次函数最值问题来求解
2、利用数形结合的方法求最值
解决解析几何问题要注意多用图形来解决问题,注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系
例 (1)已知点P为椭圆 上的动点,点A的坐标为(0,5),求的最值。
(2)设分别是椭圆的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则的最大值为________________。
(3)已知 分别是椭圆的左、右焦点,P为椭圆上任一点,若点A(0,),则 的最小值为________________。
变式训练1:
设椭圆的中心是坐标原点,长轴在轴上,离心率,已知点到这个椭圆上的点的最远距离是,求这个椭圆的方程,并求椭圆上的点到的距离等于的点的坐标。
变式训练2:
已知A(4,0)、B(2,2)是椭圆内的两个点,M是椭圆上的动点,求|MA|+|MB|的最大值和最小值。
题型 椭圆中的焦点三角形问题
关于椭圆的焦点三角形问题,可以结合椭圆的定义列出,整体代换求解,这种回归定义的方法是求解椭圆焦点三角形问题的常用方法。
在求解的过程中要注意灵活的运用正弦定理和余弦定理等。
例 已知椭圆,点P是椭圆上一点,是椭圆的焦点,且,求的面积。
题型 椭圆离心率的求法
1、定义法
当题目中出现焦点三角形三边关系或 易求时,可以利用定义求解
易求 时,可利用
易求 时,可利用
2、方程法
构建关于 的齐次式,列方程求解
例 椭圆C:的左焦点为F,若F关于直线的对称点A是椭圆C上的点,则椭圆C的离心率为____________________。
变式训练1:
(2020天津实验中学高二月考)已知椭圆的左焦点为,左顶点为,上顶点为.已知(为原点)。
(1)求椭圆的离心率;
(2)设经过点且斜率为的直线与椭圆在轴上方的交点为,圆同时与轴和直线相切,圆心在直线上,且,求椭圆的方程。
题型 点差法
1、点差法三步曲
(1)设点:设出直线与椭圆C的两个交点
(2)代入:将分别代入椭圆方程
(3)作差:两式相减,构造出,从而建立中点坐标和斜率的关系
2、点差法的结论:设直线与椭圆交于两点A、B,弦AB的中点为
(1)当椭圆的方程为时:
(2)当椭圆的方程为时:
例 已知椭圆和点,,若椭圆的某弦的中点在线段AB上,且此弦所在直线的斜率为k,则k的取值范围为_____________________。
让每一个孩子都能学有所得!
椭圆 2 / 2
课后巩固练习
一、选择题
1.(2020广东湛江高二期末)曲线与曲线的
A.长轴长相等 B.短轴长相等 C.离心率相等 D.焦距相等
2.(2020·上海黄浦高二期末)设椭圆,若四点,,,中恰有三点在椭圆上,则不在上的点为( ).
A. B. C. D.
3. (2020·湖北宜昌高二月考)设椭圆的离心率为,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.已知椭圆+y2=1,F1,F2分别是椭圆的左、右焦点,点P为椭圆上的任意一点,则的取值范围为( )
A.[1,2] B.[] C.[,4] D.[1,4]
5.(多选题)(2020·江苏省苏州中学园区校高二开学考试)如图,椭圆Ⅰ与Ⅱ有公共的左顶点和左焦点,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心.设椭圆Ⅰ与Ⅱ的长半轴长分别为和,半焦距分别为和,离心率分别为,则下列结论正确的是( )
A. B.
C. D.
6.(多选题)(2020·江苏广陵扬州中学高二月考)在平面直角坐标系中,椭圆上存在点,使得,其中、分别为椭圆的左、右焦点,则该椭圆的离心率可能为( )
A. B. C. D.
二、填空题
7.(2020·全国高二课时练)已知长方形ABCD,AB=4,BC=3,则以A,B为焦点,且过C,D的椭圆的离心率为 .
8.(2020·洋县中学高二期中)万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为__________.cm
9.(2020·南京市秦淮中学高二期中)已知椭圆的右焦点为,过点作轴的垂线交椭圆于,两点,若,则椭圆的离心率等于__________.
10. (2020·全国高二课时练)已知F是椭圆C:=1(a>b>0)的一个焦点,P是C上的任意一点,则|FP|称为椭圆C的焦半径.设C的左顶点与上顶点分别为A,B,若存在以A为圆心,|FP| 为半径的圆经过点B,则椭圆C的离心率的最小值为 。
三、解答题
11.(2020·全国高二课时练)(1)计算:
①若A1,A2是椭圆=1长轴的两个端点,P(0,2),则为?
②若A1,A2是椭圆=1长轴的两个端点,P,则为?
③若A1,A2是椭圆=1长轴的两个端点,P,则为?
(2)观察①②③,由此可得到:若A1,A2是椭圆=1(a>b>0)长轴的两个端点,P为椭圆上任意一点,则= 并证明你的结论。
12.(2020·全国高二课时练习)已知椭圆与椭圆有相同的焦点,且椭圆过点.
(1)求椭圆的标准方程;
(2)设椭圆的焦点为,点在椭圆上,且的面积为1,求点的坐标.
知识梳理
知识点 椭圆的定义
椭圆的定义:
我们把平面内与两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点;
两个焦点之间的距离叫做椭圆的焦距。
知识点 椭圆的方程
1、椭圆的标准方程
(1)焦点在 轴上:;
焦点:
图像:
(2)焦点在 轴上:;
焦点:
图像:
的关系:。
2、椭圆的一般方程
一般方程:。
充要条件:(同时满足以下三个条件,才能表示椭圆)
(1),
(2)同号,
(3)
3、共焦点的椭圆系方程
(1)与椭圆 有公共焦点的椭圆方程为:
(2)与椭圆 有公共焦点的椭圆方程为:
3、相同离心率的椭圆系方程
(1)与椭圆 有相同离心率的椭圆方程为:
(2)与椭圆 有相同离心率的椭圆方程为:
知识点 椭圆的几何性质
标准方程
范围
对称性 关于 轴、 轴对称,关于原点中心对称
顶点坐标
半轴长 长半轴长为 ,短半轴长为 ,
离心率
知识点 椭圆的离心率
椭圆的焦距与长轴长的比叫做椭圆的离心率,用 表示。即:。
离心率的取值范围:;
离心率对椭圆形状的影响:
(1) 越接近1, 就越接近 ,从而 就越小,椭圆就越扁;
(2) 越接近0, 就越接近 0,从而 就越接近 ,椭圆就越圆。
与 的关系:
知识点 椭圆的通径及有关最值
通径:过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆的通径
长度为:
最值
(1)椭圆上到中心距离最小的点是短轴的两个端点,到中心距离最大的点是长轴的两个端点
(2)椭圆上到焦点距离最大和最小的点是长轴的两个端点,距离的最大值为 ,距离最小值为
(3)对于椭圆上的点P,随着点P从长轴端点向短轴端点移动而逐渐变大,当点P在短轴端点处时,最大
(4)
(5)
知识点 关于椭圆的几个重要结论
1、弦长公式
设直线与椭圆交于两点,则:
2、焦点三角形
P为椭圆上异于长轴端点的点,则称作焦点三角形
若,则的面积:
3、椭圆的切线
椭圆 上一点 处的切线方程为
4、点与椭圆的位置关系:对于椭圆 ,我们有:
(1)在椭圆内部
(2)在椭圆外部
(3)在椭圆上
5、椭圆中斜率乘积为定值的问题
(1)椭圆 长轴的两个端点与椭圆上除这两个顶点外的任一点连线的斜率之积为
(2)设A、B是椭圆 上关于原点对称的两点,点P为该椭圆上不同于A、B的任一点,若直线PA、PB的斜率分别为,则
典型例题
题型 求椭圆的标准方程
1、定义法:验证动点到两定点的距离之和是否等于一个常数,并且该常数大于两定点之间的距离,若符合,则动点的轨迹是一个椭圆。(要注意检验);
2、待定系数法
定位置:确定焦点在哪条坐标轴上
设方程:根据焦点的位置设方程
焦点位置不确定时,分情况讨论,或者设为
寻关系:根据条件列出关于的方程组
得方程:解方程组,得到椭圆方程
例 (1)已知点,点P是圆的任意一点,线段PA的垂直平分线与直线CP交于点E。求点E的轨迹方程。
(2)求经过和两点的椭圆的标准方程。
变式训练:
已知平面内两定点,动点满足。
(1)求动点的轨迹的方程;
(2)若直线与曲线C交于不同的两点、,求。
题型 椭圆中的最值问题
1、利用求函数最值的方法求最值
将问题转化为函数的最值问题处理时,要注意 自身的取值范围,常常化为闭区间上的二次函数最值问题来求解
2、利用数形结合的方法求最值
解决解析几何问题要注意多用图形来解决问题,注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系
例 (1)已知点P为椭圆 上的动点,点A的坐标为(0,5),求的最值。
(2)设分别是椭圆的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则的最大值为________________。
(3)已知 分别是椭圆的左、右焦点,P为椭圆上任一点,若点A(0,),则 的最小值为________________。
变式训练1:
设椭圆的中心是坐标原点,长轴在轴上,离心率,已知点到这个椭圆上的点的最远距离是,求这个椭圆的方程,并求椭圆上的点到的距离等于的点的坐标。
变式训练2:
已知A(4,0)、B(2,2)是椭圆内的两个点,M是椭圆上的动点,求|MA|+|MB|的最大值和最小值。
题型 椭圆中的焦点三角形问题
关于椭圆的焦点三角形问题,可以结合椭圆的定义列出,整体代换求解,这种回归定义的方法是求解椭圆焦点三角形问题的常用方法。
在求解的过程中要注意灵活的运用正弦定理和余弦定理等。
例 已知椭圆,点P是椭圆上一点,是椭圆的焦点,且,求的面积。
题型 椭圆离心率的求法
1、定义法
当题目中出现焦点三角形三边关系或 易求时,可以利用定义求解
易求 时,可利用
易求 时,可利用
2、方程法
构建关于 的齐次式,列方程求解
例 椭圆C:的左焦点为F,若F关于直线的对称点A是椭圆C上的点,则椭圆C的离心率为____________________。
变式训练1:
(2020天津实验中学高二月考)已知椭圆的左焦点为,左顶点为,上顶点为.已知(为原点)。
(1)求椭圆的离心率;
(2)设经过点且斜率为的直线与椭圆在轴上方的交点为,圆同时与轴和直线相切,圆心在直线上,且,求椭圆的方程。
题型 点差法
1、点差法三步曲
(1)设点:设出直线与椭圆C的两个交点
(2)代入:将分别代入椭圆方程
(3)作差:两式相减,构造出,从而建立中点坐标和斜率的关系
2、点差法的结论:设直线与椭圆交于两点A、B,弦AB的中点为
(1)当椭圆的方程为时:
(2)当椭圆的方程为时:
例 已知椭圆和点,,若椭圆的某弦的中点在线段AB上,且此弦所在直线的斜率为k,则k的取值范围为_____________________。
让每一个孩子都能学有所得!
椭圆 2 / 2
课后巩固练习
一、选择题
1.(2020广东湛江高二期末)曲线与曲线的
A.长轴长相等 B.短轴长相等 C.离心率相等 D.焦距相等
2.(2020·上海黄浦高二期末)设椭圆,若四点,,,中恰有三点在椭圆上,则不在上的点为( ).
A. B. C. D.
3. (2020·湖北宜昌高二月考)设椭圆的离心率为,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.已知椭圆+y2=1,F1,F2分别是椭圆的左、右焦点,点P为椭圆上的任意一点,则的取值范围为( )
A.[1,2] B.[] C.[,4] D.[1,4]
5.(多选题)(2020·江苏省苏州中学园区校高二开学考试)如图,椭圆Ⅰ与Ⅱ有公共的左顶点和左焦点,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心.设椭圆Ⅰ与Ⅱ的长半轴长分别为和,半焦距分别为和,离心率分别为,则下列结论正确的是( )
A. B.
C. D.
6.(多选题)(2020·江苏广陵扬州中学高二月考)在平面直角坐标系中,椭圆上存在点,使得,其中、分别为椭圆的左、右焦点,则该椭圆的离心率可能为( )
A. B. C. D.
二、填空题
7.(2020·全国高二课时练)已知长方形ABCD,AB=4,BC=3,则以A,B为焦点,且过C,D的椭圆的离心率为 .
8.(2020·洋县中学高二期中)万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为__________.cm
9.(2020·南京市秦淮中学高二期中)已知椭圆的右焦点为,过点作轴的垂线交椭圆于,两点,若,则椭圆的离心率等于__________.
10. (2020·全国高二课时练)已知F是椭圆C:=1(a>b>0)的一个焦点,P是C上的任意一点,则|FP|称为椭圆C的焦半径.设C的左顶点与上顶点分别为A,B,若存在以A为圆心,|FP| 为半径的圆经过点B,则椭圆C的离心率的最小值为 。
三、解答题
11.(2020·全国高二课时练)(1)计算:
①若A1,A2是椭圆=1长轴的两个端点,P(0,2),则为?
②若A1,A2是椭圆=1长轴的两个端点,P,则为?
③若A1,A2是椭圆=1长轴的两个端点,P,则为?
(2)观察①②③,由此可得到:若A1,A2是椭圆=1(a>b>0)长轴的两个端点,P为椭圆上任意一点,则= 并证明你的结论。
12.(2020·全国高二课时练习)已知椭圆与椭圆有相同的焦点,且椭圆过点.
(1)求椭圆的标准方程;
(2)设椭圆的焦点为,点在椭圆上,且的面积为1,求点的坐标.
