吉林省长春五中高一物理《第11讲 牛顿第二定律》课件
文档属性
| 名称 | 吉林省长春五中高一物理《第11讲 牛顿第二定律》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 781.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-24 15:34:21 | ||
图片预览










文档简介
(共35张PPT)
牛顿第二定律是高考命题的热点,涉及本讲的主要考查内容有:(1)加速度与合外力的关系,主要是考查对四性的理解,尤其是瞬时性;(2)结合正交分解法运用牛顿第二定律解题;(3)在变力情况下的动力学问题分析.主要题型为选择题与计算题,试题注重知识的应用性,对运用牛顿第二定律分析解答物理过程的要求较高.
本讲要求熟练掌握牛顿第二定律的内容、表达式,深刻理解加速度与合力的关系;能熟练运用牛顿第二定律求解瞬间加速度或作用力,会分析物体在受力情况变化的过程中的速度、加速度的变化;并掌握运用正交分解法解题的方法.
本讲要求掌握加速度与合外力的四性关系;掌握运用正交分解法解题的方法与技巧;会对弹簧弹力、摩擦力等的变化的相关问题进行分析,加深对加速度与合外力的瞬时性与同向性的理解,提高分析与综合能力.
1. 质量为2 kg的物体,受到大小分别为2 N、
3 N、4 N的三个共点力的作用,则物体的加速度大小可能是 ( )
?A. 0 B. 2 m/s2
C. 4 m/s2 D. 5 m/s2
2. 物体运动的速度方向、加速度方向与物体所受合外力方向的关系是 ( )
?A. 速度方向、加速度方向、合外力方向三者总是相同的
ABC
B. 速度方向可与加速度方向成任何夹角,但加速度方向总是与合外力方向相同
C. 速度方向总是和合外力方向相同,而加速度方向可能和合外力方向相同,也可能不同
D. 速度方向、加速度方向、合外力方向之间可以成任意夹角
【答案】B
3. 物体在与其初速度始终共
线的合外力F的作用下运动.取v0
方向为正时,合外力F随时间t的变
化情况如右图所示,则在0~t1这段
时间内 ( )
A. 物体的加速度先减小后增大,速度也是先减小后增大
B. 物体的加速度先增大后减小,速度也是先增大后减小
C. 物体的加速度先减小后增大,速度一直在增大
D. 物体的加速度先减小后增大,速度一直在减小
C
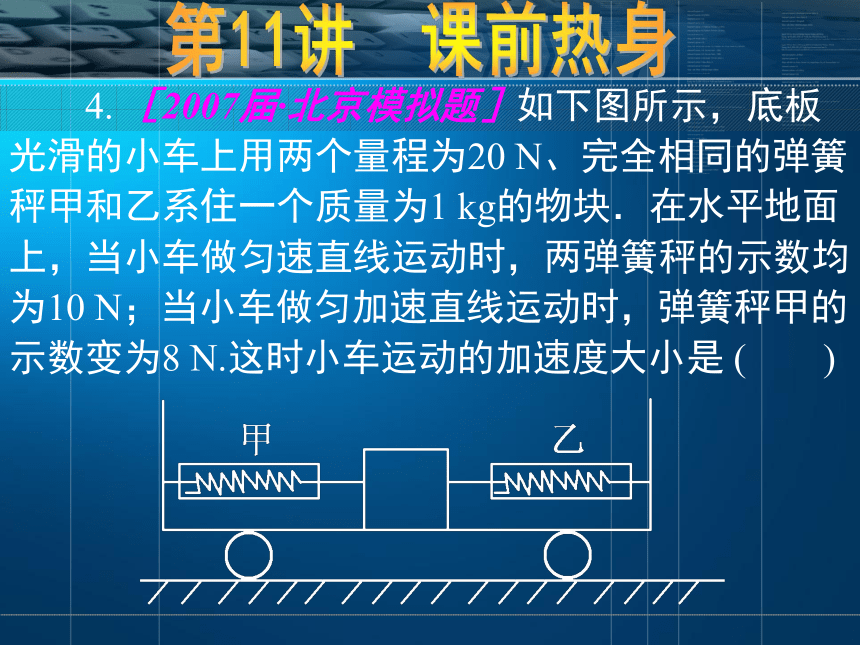
4. [2007届·北京模拟题]如下图所示,底板光滑的小车上用两个量程为20 N、完全相同的弹簧秤甲和乙系住一个质量为1 kg的物块.在水平地面上,当小车做匀速直线运动时,两弹簧秤的示数均为10 N;当小车做匀加速直线运动时,弹簧秤甲的示数变为8 N.这时小车运动的加速度大小是 ( )
?A. 2 m/s2 B. 4 m/s2
?C. 6 m/s2 D. 8 m/s2
【解析】当小车匀速运动时,两弹簧秤的示数均为10 N,合力为零,当小车匀加速运动时,甲的示数为8 N,而由于小车长度不变,则甲弹簧的形变的变化量与乙必相等,故乙弹簧的示数应为12 N,故物体受到的合力为4 N,其加速度为4 m/s2.
【答案】B
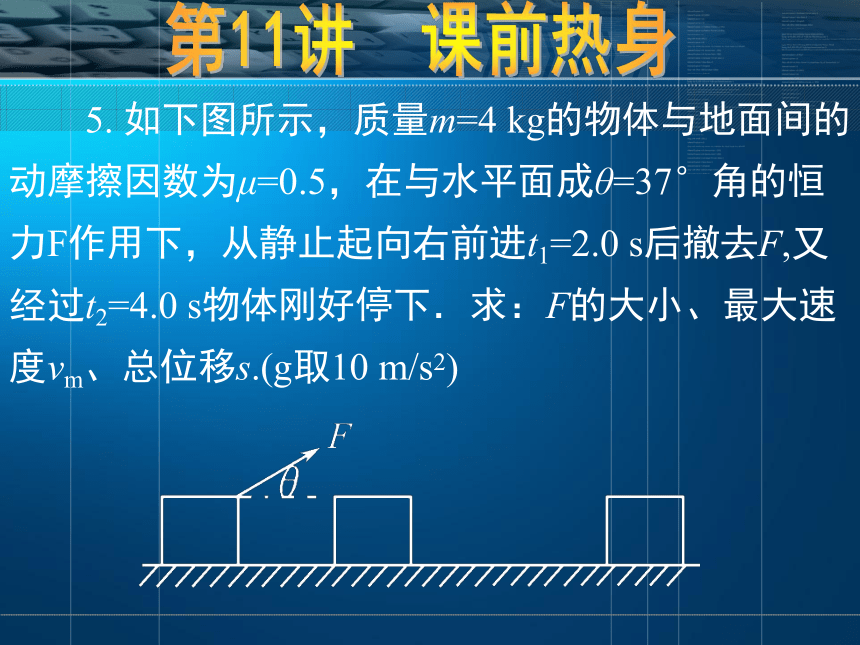
5. 如下图所示,质量m=4 kg的物体与地面间的动摩擦因数为μ=0.5,在与水平面成θ=37°角的恒力F作用下,从静止起向右前进t1=2.0 s后撤去F,又经过t2=4.0 s物体刚好停下.求:F的大小、最大速度vm、总位移s.(g取10 m/s2)
【解析】由运动学知识可知:前后两段匀变速直线运动的加速度a与时间t成反比,而第二段中μmg=ma2,加速度a2=μg=5 m/s2,所以第一段中的加速度一定是a1=10 m/s2.再由方程Fcosθ-μ(mg-Fsinθ)=ma1可求得:F=54.5N.
第一段的末速度和第二段的初速度相等且都是最大速度,第二段:vm=a2t2=20 m/s.又由于两段的平均速度和全过程的平均速度相等,所以有
s= (t1+t2)=60 m.
一、牛顿第二定律
定律内容:物体的加速度跟所受的合外力大小成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同.
表 达 式:F合=ma.
适应范围:宏观低速运动的惯性系中运动与力的问题.
二、加速度与合外力的关系(除大小成正比外,还应理解四性)
1. 同体性:在表达式中,m、F合、a都应是同一个研究对象的对应量.
?(1) 若研究对象为单个物体,则满足F合=ma;
?(2) 若研究对象为多个物体,则满足F合=m1a1+m2a2+m3a3+…(一维情况下).
2. 瞬时性:加速度和合外力具有瞬时对应关系,它们总是同增同减同生同灭.
3. 同向性:加速度与合外力的方向时时保持一致.
4. 独立性:若物体受多个力的作用,则每一个力都能独自产生各自的加速度,并且任意方向均满足Fz=maz,若在两个相互垂直的方向进行正交分解,则有:
三、应用牛顿第二定律的解题步骤
(1)明确研究对象与研究过程;
(2)分析物体的受力情况,确定其合外力;
(3)分析物体的运动情况,确定或表达物体的加速度;
(4)选取正交坐标系与正方向,运用牛顿第二定律列出方程;
(5)解答并检验.
探究点一 加速度与合外力的瞬时性关系
例1 如右图所示,小球自由下落一段时间后,落在竖直放置的弹簧上,从接触弹簧开始,到弹簧压缩到最短的过程中,小球的速度、加速度、合外力的变化情况是怎样的?
【解析】速度变大或变小取决于速度方向与加速度方向的关系(当a与v同向时v变大,当a与v反向时v变小),而加速度由合外力决定,故要分析v、a的大小变化,必须先分析小球受到的合外力的变化.
小球接触弹簧时受两个力作用:向下的重力和向上的弹力(其中重力为恒力).
在接触的头一阶段,重力大于弹力,小球合力向下,且不断变小,因而加速度也向下,加速度方向与速度方向相同,速度不断增大,直至合力为零,加速度为零,速度达到最大.在后一阶段弹力大于重力(F合=kx-mg),因而加速度向上且变大,直到速度减少至0.(注意:小球不静止在最低点,在最低点时,弹力大于重力,小球将被弹簧推向上运动,请同学们自己分析以后的运动情况)弹簧压缩到最短.
【点评】分析某一复杂运动过程,要合理地抓点分段.题中弹力等于重力这一位置是个转折点,以这个转折点把小球与弹簧接触的运动分为两个阶段进行分析.
综上分析,小球向下压缩弹簧的过程中,F合方向先向下后向上,F合先变小后变大;a方向先向下后向上,a先变小后变大;v方向向下,大小先变大后变小.(向上推的过程也是先加速后减速).
变式题 如下图所示,一质量为m的物体悬挂在长度分别为l1、l2的两根细绳上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断,求剪断瞬间物体的加速度.
(1)下面是某同学对该题的一种解法:
设l1线上拉力为FT1,l2线上拉力为FT2,重力为mg,
物体在三力作用下保持平衡:
FT1cosθ=mg,FT2=mgtanθ
剪断线的瞬间,FT2突然消失,物体即在FT2反方向获得加速度.因为mgtanθ=ma,所以加速度a=
gtanθ,方向在FT2反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2)若将图(a)中的细线l1改为长度相同、质量不计的轻弹簧,如图(b)所示,其他条件不变,求解的步骤与(1)完全相同,即a=gtanθ,你认为这个结果正确吗?请说明理由.
【解析】(1)结果不正确. 因为l2被剪断的瞬间,
l1上张力的大小发生了突变. 此瞬间FT1=mgcosθ,它与重力沿绳方向的分力抵消,重力垂直于绳方向的分力产生加速度:a=gsinθ.
(2)结果正确,因为l2被剪断的瞬间,弹簧l1的长度不能发生突变, FT1的大小方向都不变,它与重力的合力大小与FT2相等,方向相反,所以物体的加速度大小为:a=gtanθ.
【点评】本题考查的是牛顿第二定律的瞬时性及轻绳与弹簧的不同力学特性.
探究点二 加速度与合外力的同向性的应用
例2 如右图所示, 动力
小车上有一竖杆,杆端用细绳拴一质量为m的小球.当小车沿倾角为30°的斜面匀加速向上运动时,绳与杆的夹角为60°,求小车的加速度和绳中拉力大小.
【解析】分析小球的受力后,画出受力图如右图所示.其中,因加速度是沿斜面方向,故小球所受合外力也是沿斜面方向,小球的受力及力的合成如图所示,由几何关系可得:∠1=∠2=30°,所以F=mg,由F=ma得a=g.从图中可得绳中拉力为FT=
2mgcos 30°= mg.
【点评】本题利用了加速度与合外力的同向性,由加速度的方向确定了合外力的方向,进而求出了合外力的大小.
探究点三 用正交分解法解题
例3 风洞实验中可产生水平方向、 大小可调节的风力. 现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径,如下图所示.
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上做匀速运动,这时小球所受的风力为小球所受重力的0.5倍. 求小球与杆间的动摩擦因数.
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离s所需时间为多少 (sin37°=0.6,cos37°=0.8)
【解析】本题主要考查应用牛顿运动定律解决实际问题的能力. 题中将套有小球的细直杆放在我们比较陌生的风洞实验里,题目比较新颖,同时也考查了学生的理解能力及灵活应用知识的能力.
(1)设小球所受的风力为F,小球质量为m.
小球在杆上匀速运动时,F=μmg,得
(2)设杆对小球的支持力
为FN,摩擦力为Ff,小球受力情
况如右图所示,将F、mg沿杆方
向和垂直杆方向正交分解,根
据牛顿第二定律得:
由①②③可解得:
【点评】1. 正交分解法的坐标轴的选择技巧:由于加速度与合外力的方向一致,通常选取和加速度一致与垂直的两个方向建立坐标轴.这样,牛顿第二定律的分量式就变为:Fx=ma、Fy=0.
2. 解答二维受力情况下的动力学习题时,应规定一个正方向,通过符号正确表达各矢量的方向.
变式题 两个叠在一起的滑块,置于固定的、倾角为θ的斜面上,如下图所示,滑块A、B质量分别为M、m,A与斜面间的动摩擦因数为μ1,B与A之间的动摩擦因数为μ2,已知两滑块都从静止开始以相同的加速度从斜面滑下,滑块B受到的摩擦力 ( )
?A. 等于零
B. 方向沿斜面向上
?C. 大小等于μ2mgcosθ
D. 大小等于μ1mgcosθ
【解析】把A、B两滑块作为一个整体,设其下滑加速度为a,由牛顿第二定律得:
(M+m)gsinθ-μ1(M+m)gcosθ=(M+m)a.
得a=g(sinθ-μ1cosθ)
(1) (2)
【点评】由于所求的摩擦力是未知力,若设B受到A对它的摩擦力沿斜面向下,则牛顿第二定律的表达式为mgsinθ+FB=ma得FB=ma-mgsinθ=mg(sinθ-μ1cosθ)-mgsinθ=-μ1mgcosθ,式中负号表示FB的方向与规定的正方向相反,即沿斜面向上.
由于a<gsinθ,可见B随A一起下滑过程中,必须受到A对它沿斜面向上的摩擦力,设摩擦力为FB (如上图(2)所示). 由牛顿第二定律mgsinθ-FB=ma.
得FB=mgsinθ-ma=mgsinθ-mg(sinθ-μ1cosθ) =μ1mgcosθ.
【答案】BD
探究点四 变力作用下物体的运动
例4 一弹簧秤的秤盘质量m1=1.5 kg,盘内放一物体P,P的质量m2=10.5 kg,弹簧质量不计,其劲度系数k=800 N/m,系统处于静止状态,如右图所示,现给P施加一竖直向上的力F使P从静止开始向上做匀加速运动,已知在最初0.2 s内F是变力,在0.2 s后F是恒力,求F的最小值和最大值各为多少?
【解析】未施加拉力时,系统处于平衡状态,故有:kx0=(m1+m2)g.
当0≤t<0.2 s时,P匀加速上升的位移x0-x= at2.
当t=0.2 s时,P与秤盘分离(FN=0),
由牛顿第二定律F=ma得:
对秤盘:kx-m1g=m1a,
开始运动时,弹簧压缩量最大,F有最小值:
Fmin=(m1+m2)a=12×6 N=72 N
当FN=0时F有最大值:
Fmax=m2(g+a)=10.5×16 N=168 N.
【点评】本例中对于两物体分离的条件的判断是难点,也是解题的关键.可以先分析m1对m2支持力的变化特点. 对整体:F+F弹-(m1+m2)g=(m1+m2)a,随着弹簧弹力F弹减小,F增大. 再对m2有F+FN-m2g=m2a,FN将随F增大而减小,当FN减小为零时,m2与m1分离.
变式题 传送带以恒定的
速率v=10 m/s运动,已知它与水
平面成θ=37°,如右图所示,
PQ=16 m,将一个小物体无初
速地放在P点,小物体与传送带
间的动摩擦因数μ=0.5,问当
皮带逆时针转动时,小物体运动到Q点的时间为多少
【解析】当物体刚放在传送带上时,物体的速度小于传送带的速度,物体所受的滑动摩擦力方向沿斜面向下,加速度为:
当物体与传送带的速度相同时,由于重力的作用,物体继续加速,物体的速度大于传送带的速度,摩擦力的方向变为沿斜面向上,加速度为:
因为s2=s-s1=11 m
又s2=vt2+ 解得t2=1 s
所以小物体从P点运动到Q点的时间:t=t1+t2=2 s.
【点评】摩擦力的突变有多种类型,其大小突变有静静突变、动静突变、静动突变、动动突变.本题就属动动突变.在突变时还可能涉及方向的突变,这是由于摩擦力的被动性所引起的.
牛顿第二定律是高考命题的热点,涉及本讲的主要考查内容有:(1)加速度与合外力的关系,主要是考查对四性的理解,尤其是瞬时性;(2)结合正交分解法运用牛顿第二定律解题;(3)在变力情况下的动力学问题分析.主要题型为选择题与计算题,试题注重知识的应用性,对运用牛顿第二定律分析解答物理过程的要求较高.
本讲要求熟练掌握牛顿第二定律的内容、表达式,深刻理解加速度与合力的关系;能熟练运用牛顿第二定律求解瞬间加速度或作用力,会分析物体在受力情况变化的过程中的速度、加速度的变化;并掌握运用正交分解法解题的方法.
本讲要求掌握加速度与合外力的四性关系;掌握运用正交分解法解题的方法与技巧;会对弹簧弹力、摩擦力等的变化的相关问题进行分析,加深对加速度与合外力的瞬时性与同向性的理解,提高分析与综合能力.
1. 质量为2 kg的物体,受到大小分别为2 N、
3 N、4 N的三个共点力的作用,则物体的加速度大小可能是 ( )
?A. 0 B. 2 m/s2
C. 4 m/s2 D. 5 m/s2
2. 物体运动的速度方向、加速度方向与物体所受合外力方向的关系是 ( )
?A. 速度方向、加速度方向、合外力方向三者总是相同的
ABC
B. 速度方向可与加速度方向成任何夹角,但加速度方向总是与合外力方向相同
C. 速度方向总是和合外力方向相同,而加速度方向可能和合外力方向相同,也可能不同
D. 速度方向、加速度方向、合外力方向之间可以成任意夹角
【答案】B
3. 物体在与其初速度始终共
线的合外力F的作用下运动.取v0
方向为正时,合外力F随时间t的变
化情况如右图所示,则在0~t1这段
时间内 ( )
A. 物体的加速度先减小后增大,速度也是先减小后增大
B. 物体的加速度先增大后减小,速度也是先增大后减小
C. 物体的加速度先减小后增大,速度一直在增大
D. 物体的加速度先减小后增大,速度一直在减小
C
4. [2007届·北京模拟题]如下图所示,底板光滑的小车上用两个量程为20 N、完全相同的弹簧秤甲和乙系住一个质量为1 kg的物块.在水平地面上,当小车做匀速直线运动时,两弹簧秤的示数均为10 N;当小车做匀加速直线运动时,弹簧秤甲的示数变为8 N.这时小车运动的加速度大小是 ( )
?A. 2 m/s2 B. 4 m/s2
?C. 6 m/s2 D. 8 m/s2
【解析】当小车匀速运动时,两弹簧秤的示数均为10 N,合力为零,当小车匀加速运动时,甲的示数为8 N,而由于小车长度不变,则甲弹簧的形变的变化量与乙必相等,故乙弹簧的示数应为12 N,故物体受到的合力为4 N,其加速度为4 m/s2.
【答案】B
5. 如下图所示,质量m=4 kg的物体与地面间的动摩擦因数为μ=0.5,在与水平面成θ=37°角的恒力F作用下,从静止起向右前进t1=2.0 s后撤去F,又经过t2=4.0 s物体刚好停下.求:F的大小、最大速度vm、总位移s.(g取10 m/s2)
【解析】由运动学知识可知:前后两段匀变速直线运动的加速度a与时间t成反比,而第二段中μmg=ma2,加速度a2=μg=5 m/s2,所以第一段中的加速度一定是a1=10 m/s2.再由方程Fcosθ-μ(mg-Fsinθ)=ma1可求得:F=54.5N.
第一段的末速度和第二段的初速度相等且都是最大速度,第二段:vm=a2t2=20 m/s.又由于两段的平均速度和全过程的平均速度相等,所以有
s= (t1+t2)=60 m.
一、牛顿第二定律
定律内容:物体的加速度跟所受的合外力大小成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同.
表 达 式:F合=ma.
适应范围:宏观低速运动的惯性系中运动与力的问题.
二、加速度与合外力的关系(除大小成正比外,还应理解四性)
1. 同体性:在表达式中,m、F合、a都应是同一个研究对象的对应量.
?(1) 若研究对象为单个物体,则满足F合=ma;
?(2) 若研究对象为多个物体,则满足F合=m1a1+m2a2+m3a3+…(一维情况下).
2. 瞬时性:加速度和合外力具有瞬时对应关系,它们总是同增同减同生同灭.
3. 同向性:加速度与合外力的方向时时保持一致.
4. 独立性:若物体受多个力的作用,则每一个力都能独自产生各自的加速度,并且任意方向均满足Fz=maz,若在两个相互垂直的方向进行正交分解,则有:
三、应用牛顿第二定律的解题步骤
(1)明确研究对象与研究过程;
(2)分析物体的受力情况,确定其合外力;
(3)分析物体的运动情况,确定或表达物体的加速度;
(4)选取正交坐标系与正方向,运用牛顿第二定律列出方程;
(5)解答并检验.
探究点一 加速度与合外力的瞬时性关系
例1 如右图所示,小球自由下落一段时间后,落在竖直放置的弹簧上,从接触弹簧开始,到弹簧压缩到最短的过程中,小球的速度、加速度、合外力的变化情况是怎样的?
【解析】速度变大或变小取决于速度方向与加速度方向的关系(当a与v同向时v变大,当a与v反向时v变小),而加速度由合外力决定,故要分析v、a的大小变化,必须先分析小球受到的合外力的变化.
小球接触弹簧时受两个力作用:向下的重力和向上的弹力(其中重力为恒力).
在接触的头一阶段,重力大于弹力,小球合力向下,且不断变小,因而加速度也向下,加速度方向与速度方向相同,速度不断增大,直至合力为零,加速度为零,速度达到最大.在后一阶段弹力大于重力(F合=kx-mg),因而加速度向上且变大,直到速度减少至0.(注意:小球不静止在最低点,在最低点时,弹力大于重力,小球将被弹簧推向上运动,请同学们自己分析以后的运动情况)弹簧压缩到最短.
【点评】分析某一复杂运动过程,要合理地抓点分段.题中弹力等于重力这一位置是个转折点,以这个转折点把小球与弹簧接触的运动分为两个阶段进行分析.
综上分析,小球向下压缩弹簧的过程中,F合方向先向下后向上,F合先变小后变大;a方向先向下后向上,a先变小后变大;v方向向下,大小先变大后变小.(向上推的过程也是先加速后减速).
变式题 如下图所示,一质量为m的物体悬挂在长度分别为l1、l2的两根细绳上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断,求剪断瞬间物体的加速度.
(1)下面是某同学对该题的一种解法:
设l1线上拉力为FT1,l2线上拉力为FT2,重力为mg,
物体在三力作用下保持平衡:
FT1cosθ=mg,FT2=mgtanθ
剪断线的瞬间,FT2突然消失,物体即在FT2反方向获得加速度.因为mgtanθ=ma,所以加速度a=
gtanθ,方向在FT2反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2)若将图(a)中的细线l1改为长度相同、质量不计的轻弹簧,如图(b)所示,其他条件不变,求解的步骤与(1)完全相同,即a=gtanθ,你认为这个结果正确吗?请说明理由.
【解析】(1)结果不正确. 因为l2被剪断的瞬间,
l1上张力的大小发生了突变. 此瞬间FT1=mgcosθ,它与重力沿绳方向的分力抵消,重力垂直于绳方向的分力产生加速度:a=gsinθ.
(2)结果正确,因为l2被剪断的瞬间,弹簧l1的长度不能发生突变, FT1的大小方向都不变,它与重力的合力大小与FT2相等,方向相反,所以物体的加速度大小为:a=gtanθ.
【点评】本题考查的是牛顿第二定律的瞬时性及轻绳与弹簧的不同力学特性.
探究点二 加速度与合外力的同向性的应用
例2 如右图所示, 动力
小车上有一竖杆,杆端用细绳拴一质量为m的小球.当小车沿倾角为30°的斜面匀加速向上运动时,绳与杆的夹角为60°,求小车的加速度和绳中拉力大小.
【解析】分析小球的受力后,画出受力图如右图所示.其中,因加速度是沿斜面方向,故小球所受合外力也是沿斜面方向,小球的受力及力的合成如图所示,由几何关系可得:∠1=∠2=30°,所以F=mg,由F=ma得a=g.从图中可得绳中拉力为FT=
2mgcos 30°= mg.
【点评】本题利用了加速度与合外力的同向性,由加速度的方向确定了合外力的方向,进而求出了合外力的大小.
探究点三 用正交分解法解题
例3 风洞实验中可产生水平方向、 大小可调节的风力. 现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径,如下图所示.
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上做匀速运动,这时小球所受的风力为小球所受重力的0.5倍. 求小球与杆间的动摩擦因数.
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离s所需时间为多少 (sin37°=0.6,cos37°=0.8)
【解析】本题主要考查应用牛顿运动定律解决实际问题的能力. 题中将套有小球的细直杆放在我们比较陌生的风洞实验里,题目比较新颖,同时也考查了学生的理解能力及灵活应用知识的能力.
(1)设小球所受的风力为F,小球质量为m.
小球在杆上匀速运动时,F=μmg,得
(2)设杆对小球的支持力
为FN,摩擦力为Ff,小球受力情
况如右图所示,将F、mg沿杆方
向和垂直杆方向正交分解,根
据牛顿第二定律得:
由①②③可解得:
【点评】1. 正交分解法的坐标轴的选择技巧:由于加速度与合外力的方向一致,通常选取和加速度一致与垂直的两个方向建立坐标轴.这样,牛顿第二定律的分量式就变为:Fx=ma、Fy=0.
2. 解答二维受力情况下的动力学习题时,应规定一个正方向,通过符号正确表达各矢量的方向.
变式题 两个叠在一起的滑块,置于固定的、倾角为θ的斜面上,如下图所示,滑块A、B质量分别为M、m,A与斜面间的动摩擦因数为μ1,B与A之间的动摩擦因数为μ2,已知两滑块都从静止开始以相同的加速度从斜面滑下,滑块B受到的摩擦力 ( )
?A. 等于零
B. 方向沿斜面向上
?C. 大小等于μ2mgcosθ
D. 大小等于μ1mgcosθ
【解析】把A、B两滑块作为一个整体,设其下滑加速度为a,由牛顿第二定律得:
(M+m)gsinθ-μ1(M+m)gcosθ=(M+m)a.
得a=g(sinθ-μ1cosθ)
(1) (2)
【点评】由于所求的摩擦力是未知力,若设B受到A对它的摩擦力沿斜面向下,则牛顿第二定律的表达式为mgsinθ+FB=ma得FB=ma-mgsinθ=mg(sinθ-μ1cosθ)-mgsinθ=-μ1mgcosθ,式中负号表示FB的方向与规定的正方向相反,即沿斜面向上.
由于a<gsinθ,可见B随A一起下滑过程中,必须受到A对它沿斜面向上的摩擦力,设摩擦力为FB (如上图(2)所示). 由牛顿第二定律mgsinθ-FB=ma.
得FB=mgsinθ-ma=mgsinθ-mg(sinθ-μ1cosθ) =μ1mgcosθ.
【答案】BD
探究点四 变力作用下物体的运动
例4 一弹簧秤的秤盘质量m1=1.5 kg,盘内放一物体P,P的质量m2=10.5 kg,弹簧质量不计,其劲度系数k=800 N/m,系统处于静止状态,如右图所示,现给P施加一竖直向上的力F使P从静止开始向上做匀加速运动,已知在最初0.2 s内F是变力,在0.2 s后F是恒力,求F的最小值和最大值各为多少?
【解析】未施加拉力时,系统处于平衡状态,故有:kx0=(m1+m2)g.
当0≤t<0.2 s时,P匀加速上升的位移x0-x= at2.
当t=0.2 s时,P与秤盘分离(FN=0),
由牛顿第二定律F=ma得:
对秤盘:kx-m1g=m1a,
开始运动时,弹簧压缩量最大,F有最小值:
Fmin=(m1+m2)a=12×6 N=72 N
当FN=0时F有最大值:
Fmax=m2(g+a)=10.5×16 N=168 N.
【点评】本例中对于两物体分离的条件的判断是难点,也是解题的关键.可以先分析m1对m2支持力的变化特点. 对整体:F+F弹-(m1+m2)g=(m1+m2)a,随着弹簧弹力F弹减小,F增大. 再对m2有F+FN-m2g=m2a,FN将随F增大而减小,当FN减小为零时,m2与m1分离.
变式题 传送带以恒定的
速率v=10 m/s运动,已知它与水
平面成θ=37°,如右图所示,
PQ=16 m,将一个小物体无初
速地放在P点,小物体与传送带
间的动摩擦因数μ=0.5,问当
皮带逆时针转动时,小物体运动到Q点的时间为多少
【解析】当物体刚放在传送带上时,物体的速度小于传送带的速度,物体所受的滑动摩擦力方向沿斜面向下,加速度为:
当物体与传送带的速度相同时,由于重力的作用,物体继续加速,物体的速度大于传送带的速度,摩擦力的方向变为沿斜面向上,加速度为:
因为s2=s-s1=11 m
又s2=vt2+ 解得t2=1 s
所以小物体从P点运动到Q点的时间:t=t1+t2=2 s.
【点评】摩擦力的突变有多种类型,其大小突变有静静突变、动静突变、静动突变、动动突变.本题就属动动突变.在突变时还可能涉及方向的突变,这是由于摩擦力的被动性所引起的.
同课章节目录
