2021春北师版九下数学2.2二次函数y=a(x-h)2图象与性质课件(17张)
文档属性
| 名称 | 2021春北师版九下数学2.2二次函数y=a(x-h)2图象与性质课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 14:23:34 | ||
图片预览




文档简介
(共17张PPT)
2二次函数y=a(x-h) 的图象
和性质
顶点坐标
对称轴
图象
开口方向
图象极点
函数极值
增减 性
a>0
a<0
(0 ,k)
y轴
向上
向下
当x=0时,y的最小值为k.
当x=0时,y的最大值为k.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,y随着x的增大而减小.
顶点是最低点
顶点是最高点
二次函数y=ax2+k( )的
顶点位置及开口方向和大小确定后,其他性质也随之确定
x
y
O
y
x
温故知新
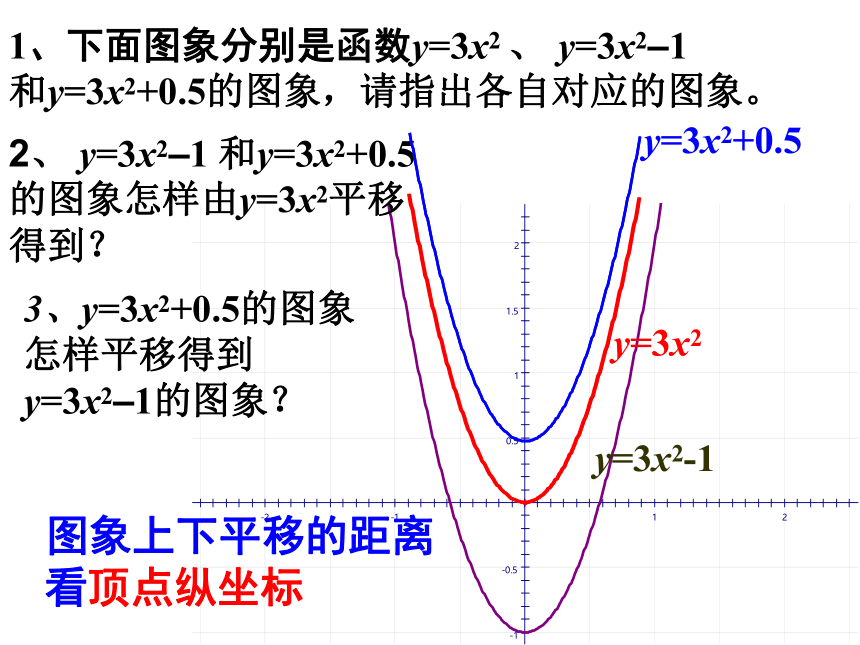
1、下面图象分别是函数y=3x2 、 y=3x2–1
和y=3x2+0.5的图象,请指出各自对应的图象。
y=3x2
y=3x2-1
y=3x2+0.5
2、 y=3x2–1 和y=3x2+0.5
的图象怎样由y=3x2平移
得到?
3、y=3x2+0.5的图象
怎样平移得到
y=3x2–1的图象?
图象上下平移的距离
看顶点纵坐标
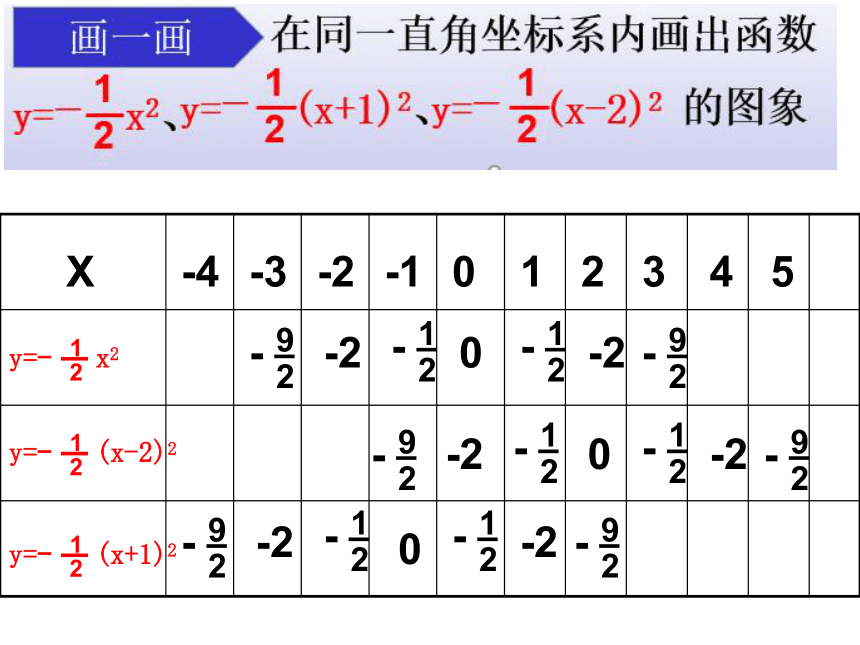
二次函数 的图象和性质
思考:
我们知道函数y=ax2的图象上下平移可以得到函数y=ax2+k的图象。
那么函数y=ax2 的图象左右平移又会怎样呢?
y=a(x-h)2
-4
-3
-2
-1
0
4
5
3
2
1
X
0
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
0
0
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
-1
-2
-2
2
-3
3
-4
-5
5
4
-4
-3
-1
1
o
1
x
y
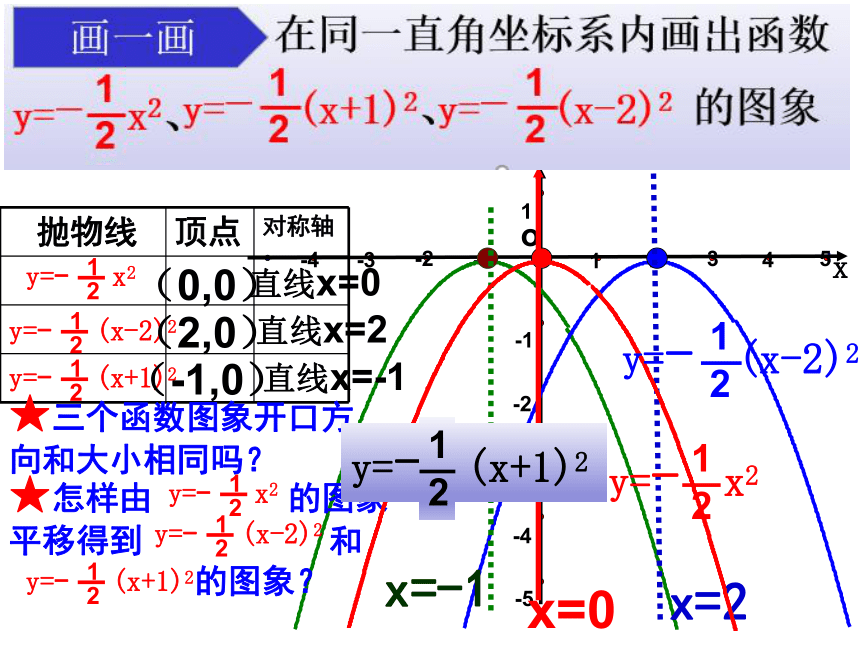
抛物线 顶点 对称轴
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
★三个函数图象开口方
向和大小相同吗?
★怎样由 的图象
平移得到 和
的图象?
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
(0,0)
直线x=0
x=2
(2,0)
直线x=2
x=-1
(-1,0)
直线x=-1
x=0
y=- x2
1
2
y=- (x-2)2
1
2
如图是函数 的图象,经过平移后得到 两个新抛物线,你能写出这两个新图象各自的解析式吗?
☆ 根据解析式判断顶点
坐标和对称轴有什么规律?
x=-2
x=1.5
x=0
抛物线 顶点
坐标 对称
轴
(0,0)
直线x=0
(-2,0)
(1.5,0)
直线x=-2
直线x=1.5
☆ 图象左右平移有
什么规律?
的图象是 。
的图象开口方向和
大小相同是由什么决定的?
的顶点坐标是 。
通过 得到。
抛物线
a相同则开口方向和大小相同
(h,0)
左右平移
左右平移的距离看顶点横坐标
归纳总结
顶点坐标
对称轴
图象
开口方向
图象极点
函数极值
增减 性
a>0
a<0
(h ,0)
直线x=h
向上
向下
当x=0时,y的最小值为0.
当x=0时,y的最大值为0.
当x当x>h时,y随着x的增大而增大.
当x当x>h时,y随着x的增大而减小.
顶点是最低点
顶点是最高点
x
y
O
y
x
函数y=a(x-h)2 ( )的
顶点位置及开口方向和大小确定后,其他性质也随之确定
(h ,0)
x=h
(h ,0)
x=h
性质归纳
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
解(1)∵a=-3<0
∴开口向下
对称轴:
直线 x= 1
顶点:
(1,0)
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
学以致用
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
解(2)∵a=4>0
∴开口向上
对称轴:
直线 x=3
顶点:
(3,0)
学以致用
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
解(3)∵a=2>0
∴开口向上
对称轴:
直线 x=-3
顶点:
(-3,0)
y=2〔x-(-3)〕2
学以致用
抛物线 开口方向 顶点坐标 对称 轴 图像草图 当X= 时
y有最 值是 。 当x 时y随x的增大而增大
y=-(x-3)2
y=2(x-4)2
y=3(x+4)2
y=-3x +1
y=2x -6
知识总结
y=3(x+2)2
1.已知抛物线y=3x2
y=3(x-3)2
将它向右平移3个单位得:
将它向左平移2个单位得:
2.将抛物线y=3(x+2)2向左平移3个单位得抛物线
将抛物线y=3(x+2)2向右平移3个单位得抛物线
y=3(x+5)2
y=3(x-1)2
学以致用
y=2x2
右
3
(1)将抛物线y=-3x2向左平移3个单位得到抛物线
y=-3(x+3)2
(2)将抛物线y=2x2-3先向上平移3单位,就得到函数 的图象,再向 平移 个单位得到函数y= 2(x-3)2的图象.
学以致用
1、把抛物线y= a(x-4)2向左平移6个单
位后得到抛物线y= -3(x-h)2的图象,
若抛物线y= a(x-4)2的顶点A,且与y
轴交于点B,抛物线y= - 3(x-h)2的
顶点是M。求ΔMAB的面积.
sΔMAB=144
a=-3 h=-2
拓展延伸
-1
-2
-2
2
-3
3
-4
-5
5
4
-4
-3
-1
1
o
1
x
y
y=-x2
y=-(x+1)2
y=-(x-1)2
拓展延伸
2二次函数y=a(x-h) 的图象
和性质
顶点坐标
对称轴
图象
开口方向
图象极点
函数极值
增减 性
a>0
a<0
(0 ,k)
y轴
向上
向下
当x=0时,y的最小值为k.
当x=0时,y的最大值为k.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,y随着x的增大而减小.
顶点是最低点
顶点是最高点
二次函数y=ax2+k( )的
顶点位置及开口方向和大小确定后,其他性质也随之确定
x
y
O
y
x
温故知新
1、下面图象分别是函数y=3x2 、 y=3x2–1
和y=3x2+0.5的图象,请指出各自对应的图象。
y=3x2
y=3x2-1
y=3x2+0.5
2、 y=3x2–1 和y=3x2+0.5
的图象怎样由y=3x2平移
得到?
3、y=3x2+0.5的图象
怎样平移得到
y=3x2–1的图象?
图象上下平移的距离
看顶点纵坐标
二次函数 的图象和性质
思考:
我们知道函数y=ax2的图象上下平移可以得到函数y=ax2+k的图象。
那么函数y=ax2 的图象左右平移又会怎样呢?
y=a(x-h)2
-4
-3
-2
-1
0
4
5
3
2
1
X
0
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
-2
-2
-
2
1
-
2
1
-
2
9
-
2
9
0
0
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
-1
-2
-2
2
-3
3
-4
-5
5
4
-4
-3
-1
1
o
1
x
y
抛物线 顶点 对称轴
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
★三个函数图象开口方
向和大小相同吗?
★怎样由 的图象
平移得到 和
的图象?
y=- x2
1
2
y=- (x-2)2
1
2
y=- (x+1)2
1
2
(0,0)
直线x=0
x=2
(2,0)
直线x=2
x=-1
(-1,0)
直线x=-1
x=0
y=- x2
1
2
y=- (x-2)2
1
2
如图是函数 的图象,经过平移后得到 两个新抛物线,你能写出这两个新图象各自的解析式吗?
☆ 根据解析式判断顶点
坐标和对称轴有什么规律?
x=-2
x=1.5
x=0
抛物线 顶点
坐标 对称
轴
(0,0)
直线x=0
(-2,0)
(1.5,0)
直线x=-2
直线x=1.5
☆ 图象左右平移有
什么规律?
的图象是 。
的图象开口方向和
大小相同是由什么决定的?
的顶点坐标是 。
通过 得到。
抛物线
a相同则开口方向和大小相同
(h,0)
左右平移
左右平移的距离看顶点横坐标
归纳总结
顶点坐标
对称轴
图象
开口方向
图象极点
函数极值
增减 性
a>0
a<0
(h ,0)
直线x=h
向上
向下
当x=0时,y的最小值为0.
当x=0时,y的最大值为0.
当x
当x
顶点是最低点
顶点是最高点
x
y
O
y
x
函数y=a(x-h)2 ( )的
顶点位置及开口方向和大小确定后,其他性质也随之确定
(h ,0)
x=h
(h ,0)
x=h
性质归纳
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
解(1)∵a=-3<0
∴开口向下
对称轴:
直线 x= 1
顶点:
(1,0)
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
学以致用
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
解(2)∵a=4>0
∴开口向上
对称轴:
直线 x=3
顶点:
(3,0)
学以致用
例1.说出下列抛物线的开口方向、
对称轴及 顶点坐标:
(1)y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2
解(3)∵a=2>0
∴开口向上
对称轴:
直线 x=-3
顶点:
(-3,0)
y=2〔x-(-3)〕2
学以致用
抛物线 开口方向 顶点坐标 对称 轴 图像草图 当X= 时
y有最 值是 。 当x 时y随x的增大而增大
y=-(x-3)2
y=2(x-4)2
y=3(x+4)2
y=-3x +1
y=2x -6
知识总结
y=3(x+2)2
1.已知抛物线y=3x2
y=3(x-3)2
将它向右平移3个单位得:
将它向左平移2个单位得:
2.将抛物线y=3(x+2)2向左平移3个单位得抛物线
将抛物线y=3(x+2)2向右平移3个单位得抛物线
y=3(x+5)2
y=3(x-1)2
学以致用
y=2x2
右
3
(1)将抛物线y=-3x2向左平移3个单位得到抛物线
y=-3(x+3)2
(2)将抛物线y=2x2-3先向上平移3单位,就得到函数 的图象,再向 平移 个单位得到函数y= 2(x-3)2的图象.
学以致用
1、把抛物线y= a(x-4)2向左平移6个单
位后得到抛物线y= -3(x-h)2的图象,
若抛物线y= a(x-4)2的顶点A,且与y
轴交于点B,抛物线y= - 3(x-h)2的
顶点是M。求ΔMAB的面积.
sΔMAB=144
a=-3 h=-2
拓展延伸
-1
-2
-2
2
-3
3
-4
-5
5
4
-4
-3
-1
1
o
1
x
y
y=-x2
y=-(x+1)2
y=-(x-1)2
拓展延伸
