2021-2022学年人教版八年级数学上册11.3.1多边形课件(16张)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3.1多边形课件(16张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 11:35:17 | ||
图片预览



文档简介
(共16张PPT)
§11.3.1多边形
学习目标
1、理解多边形的定义,多边形的内、外角及凸多边形的有关概念。
2、掌握多边形的对角线的有关概念,会求多边形的对角线条数并会用它解决简单的实际问题。
欣赏图片:
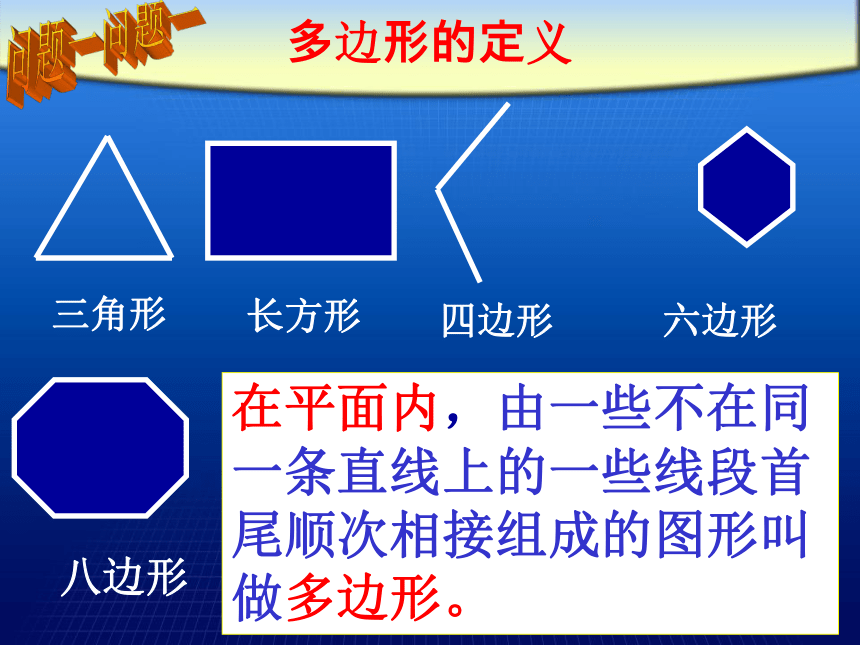
三角形
长方形
六边形
四边形
八边形
在平面内,由一些不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
问题一
多边形的
有关概念
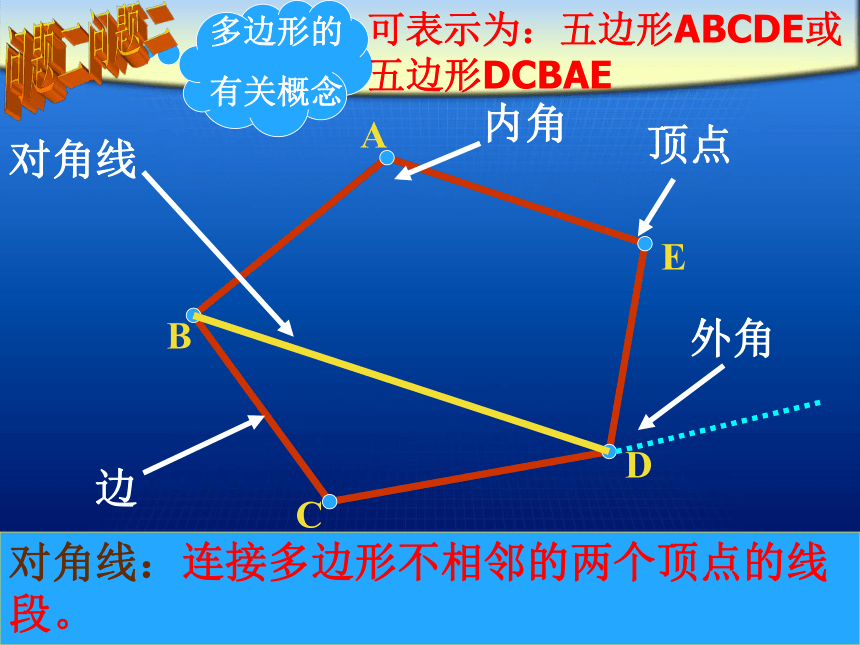
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线 段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
问题二
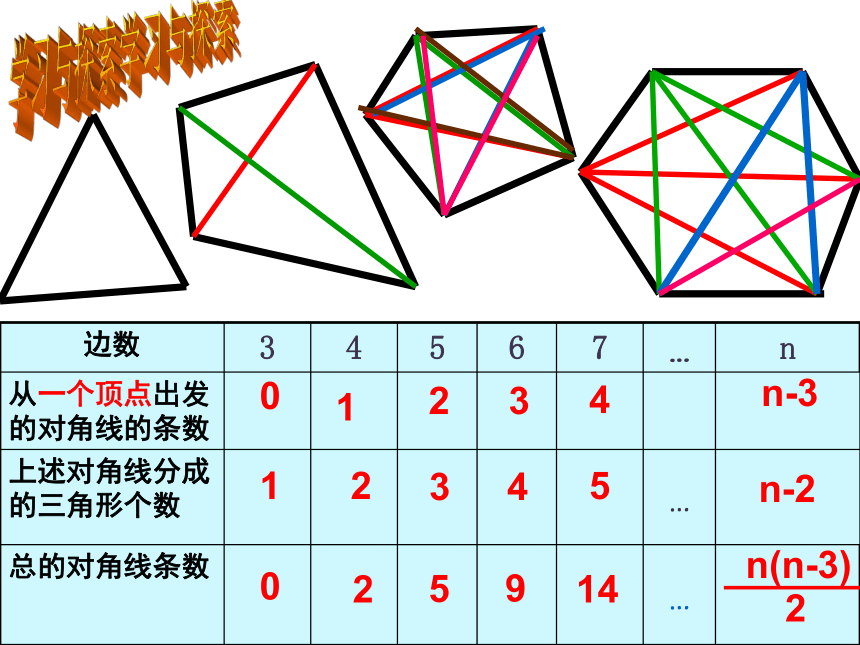
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
3
5
2
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
学习与探索
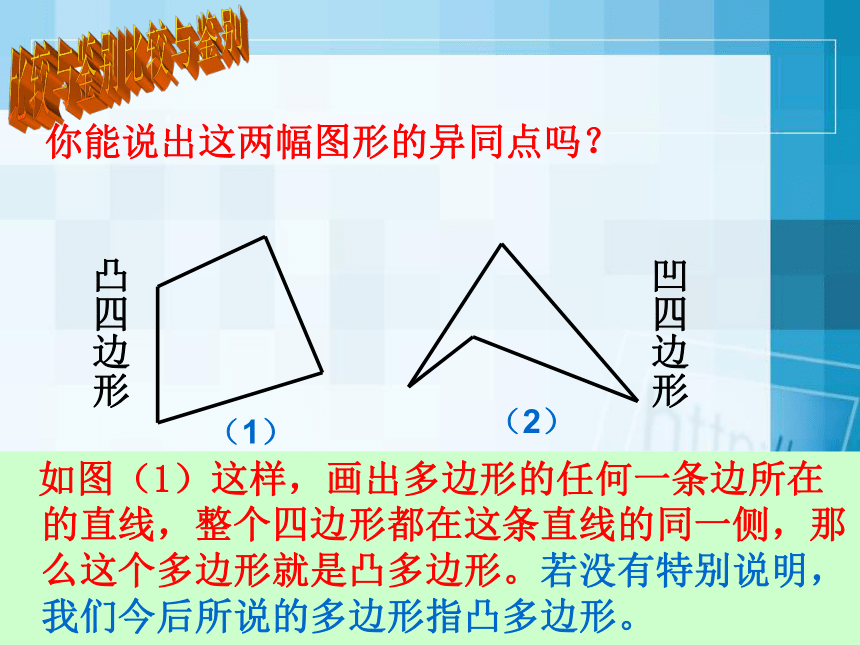
你能说出这两幅图形的异同点吗?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个四边形都在这条直线的同一侧,那么这个多边形就是凸多边形。若没有特别说明,我们今后所说的多边形指凸多边形。
凸四边形
凹四边形
比较与鉴别
正多边形
在平面内,内角都相等,边也都相等的多边形叫做正多边形
等边三角形
正方形
正五边形
正六边形
1、如果一个多边形的各边都相等,那么它是正多边形;
2、如果一个多边形的所有内角都相等,那么它是正多边形;
下列说法正确吗?如果不正确,你能用一个例子作出说明吗?
1.下列不是凸多边形的是( )
A B C D
2. 下列图形中∠1是外角的是( )
A B C D
3.下列说法正确的是( )
A.一个多边形外角的个数与边数相同。
B. 一个多边形外角的个数是边数的二倍。
C.每个角都相等的多边形是正多边形。
D.每条边都相等的多边形是正多边形。
C
1
1
1
1
D
B
随堂练
十边形共有( )条对角线
35
试一试
1、已知一个多边形从一个顶点出发有7条对角线,你能求出它的边数吗? 若该多边形共有35条对角线,你能求出它的边数吗?
2、有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,则一共要握手多少次?
(2)若一共握手170次,则参加会议的人数是多少?
拓展与提升
小结
1、多边形的定义及其内角、外角?
2、多边形的对角线及其求法;
3、凸多边形与正多边形。
达标检测:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形
B、如果画出多边形某一条边所在的直线,这个多边形都在这条直线的同一侧,那么它一定是凸多边形
C、每个角都相等的多边形叫正多边形
D、每条边、每个角都相等的多边形叫正多边形
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
3、多边形的内角是指_____________________
多边形的外角是指 _______________________
____________;
多边形的内角和它相邻的外角是________关系
D
D
多边形相邻两边组成的角
多边形的边与它的邻边 的延长线组成的角。
邻补角
1、如图,试计算∠BOC的度数.
知识回顾:
D
⌒
110°
A
B
C
O
90
20
30
2、如图,在直角△ABC中,
∠ACB= 90°, CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
A
B
C
O
90
20
30
§11.3.1多边形
学习目标
1、理解多边形的定义,多边形的内、外角及凸多边形的有关概念。
2、掌握多边形的对角线的有关概念,会求多边形的对角线条数并会用它解决简单的实际问题。
欣赏图片:
三角形
长方形
六边形
四边形
八边形
在平面内,由一些不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
问题一
多边形的
有关概念
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线 段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
问题二
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
3
5
2
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
学习与探索
你能说出这两幅图形的异同点吗?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个四边形都在这条直线的同一侧,那么这个多边形就是凸多边形。若没有特别说明,我们今后所说的多边形指凸多边形。
凸四边形
凹四边形
比较与鉴别
正多边形
在平面内,内角都相等,边也都相等的多边形叫做正多边形
等边三角形
正方形
正五边形
正六边形
1、如果一个多边形的各边都相等,那么它是正多边形;
2、如果一个多边形的所有内角都相等,那么它是正多边形;
下列说法正确吗?如果不正确,你能用一个例子作出说明吗?
1.下列不是凸多边形的是( )
A B C D
2. 下列图形中∠1是外角的是( )
A B C D
3.下列说法正确的是( )
A.一个多边形外角的个数与边数相同。
B. 一个多边形外角的个数是边数的二倍。
C.每个角都相等的多边形是正多边形。
D.每条边都相等的多边形是正多边形。
C
1
1
1
1
D
B
随堂练
十边形共有( )条对角线
35
试一试
1、已知一个多边形从一个顶点出发有7条对角线,你能求出它的边数吗? 若该多边形共有35条对角线,你能求出它的边数吗?
2、有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,则一共要握手多少次?
(2)若一共握手170次,则参加会议的人数是多少?
拓展与提升
小结
1、多边形的定义及其内角、外角?
2、多边形的对角线及其求法;
3、凸多边形与正多边形。
达标检测:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形
B、如果画出多边形某一条边所在的直线,这个多边形都在这条直线的同一侧,那么它一定是凸多边形
C、每个角都相等的多边形叫正多边形
D、每条边、每个角都相等的多边形叫正多边形
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
3、多边形的内角是指_____________________
多边形的外角是指 _______________________
____________;
多边形的内角和它相邻的外角是________关系
D
D
多边形相邻两边组成的角
多边形的边与它的邻边 的延长线组成的角。
邻补角
1、如图,试计算∠BOC的度数.
知识回顾:
D
⌒
110°
A
B
C
O
90
20
30
2、如图,在直角△ABC中,
∠ACB= 90°, CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
A
B
C
O
90
20
30
