2021—2022学年人教版数学八年级上册11.2.2三角形的外角课件(42张)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册11.2.2三角形的外角课件(42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 11:37:21 | ||
图片预览



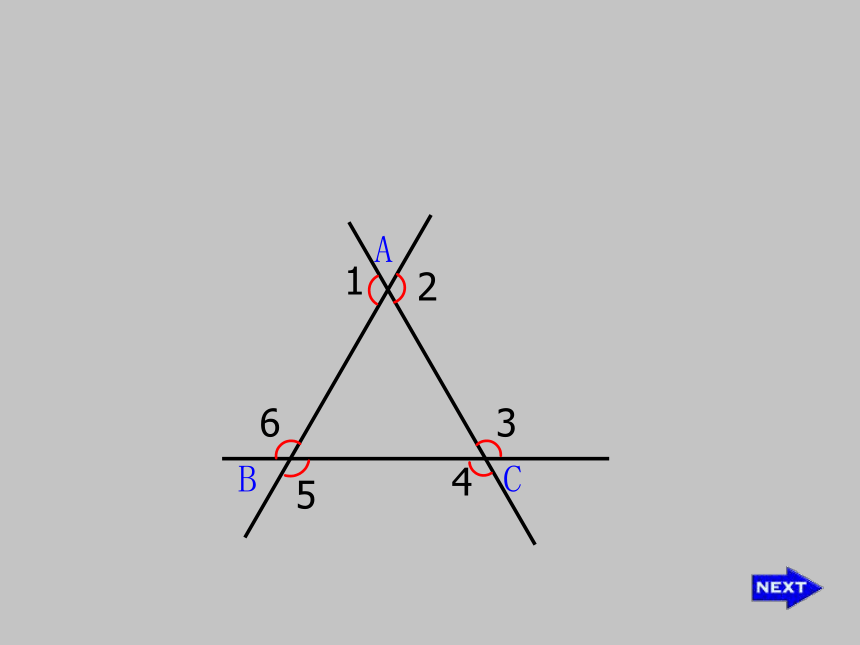




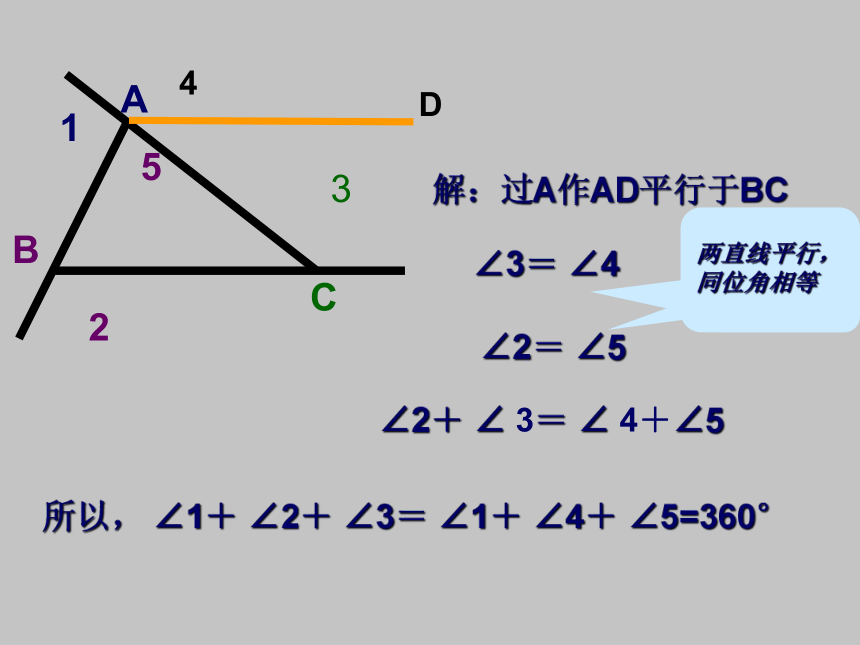
文档简介
(共42张PPT)
三角形的外角
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
D
三角形的外角
画图:
画出三角形的所有外角,思考它们之间有什么关系
A
B
C
1
2
3
4
5
6
探究:
如图,△ABC中,∠A=700,∠B=600,∠ACD是△ABC的一个外角.
(1)能由∠A,∠B求出∠ACD吗
(2)思考∠ACD与∠A,∠B有什么关系
A
B
C
700
600
D
500
1300
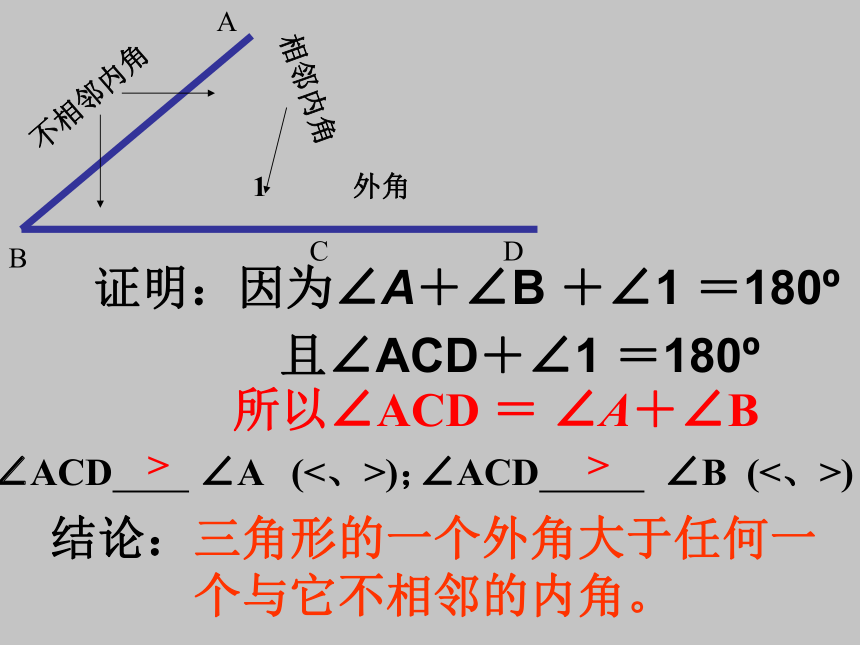
外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
外角
相邻内角
不相邻内角
1
A
B
C
D
所以∠ACD = ∠A+∠B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
>
>
结论:三角形的一个外角大于任何一个与它不相邻的内角。
证明:因为∠A+∠B +∠1 =180
且∠ACD+∠1 =180
比较∠1 和∠2的大小:
2
1
2
1
2
P
A
B
C
D
1
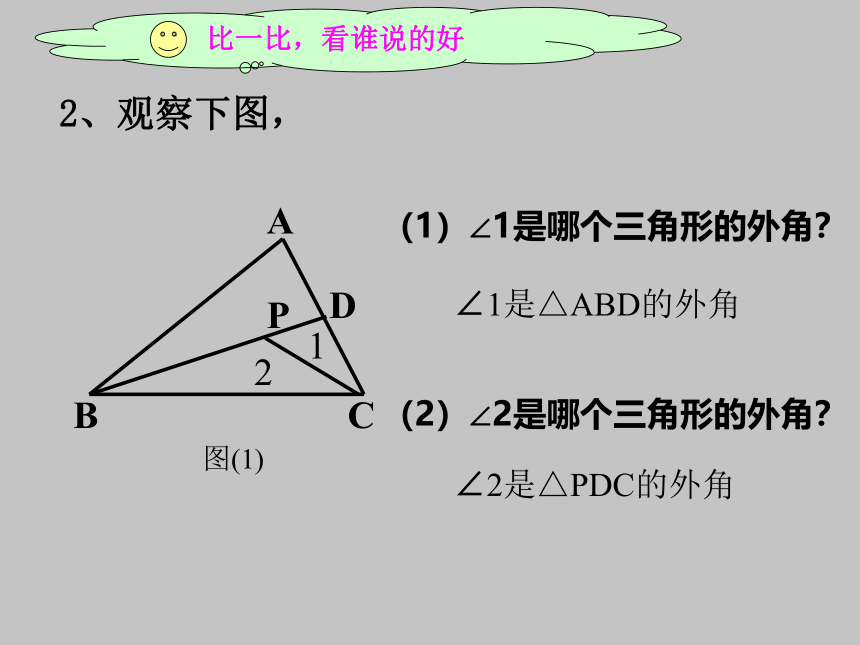
2、观察下图,
比一比,看谁说的好
图(1)
(1)∠1是哪个三角形的外角?
(2)∠2是哪个三角形的外角?
∠1是△ABD的外角
∠2是△PDC的外角
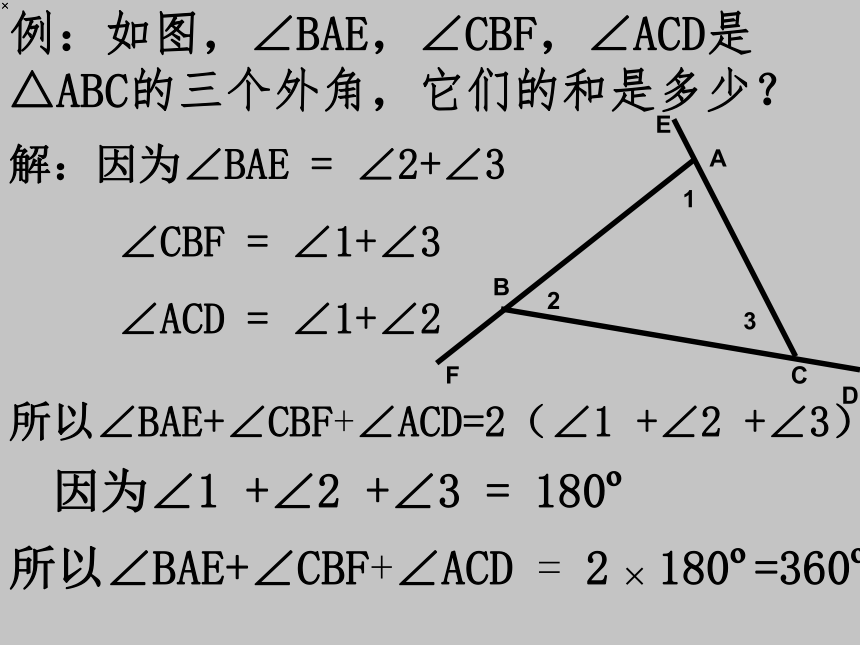
例:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
1
B
2
F
3
C
D
A
E
解:因为∠BAE = ∠2+∠3
∠CBF = ∠1+∠3
∠ACD = ∠1+∠2
所以∠BAE+∠CBF+∠ACD=2(∠1 +∠2 +∠3)
因为∠1 +∠2 +∠3 = 180
所以∠BAE+∠CBF+∠ACD = 2 180 =360
结论:三角形的外角和等于360°
你还有别的证明方法吗?
解:过A作AD平行于BC
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠5
所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠5=360°
两直线平行,同位角相等
D
∠2+ ∠ 3= ∠ 4+∠5
5
判断题:
1、三角形的一个外角等于两个内角的和.( )
2、三角形的一个外角大于任何一个内角.( )
如图:D是 ABC的BC边上一点, B= BAD,
ADC=80°, BAC= 70°.
求:(1) B的度数;
(2) C的度数.
试一试
AD平分∠BAC
说出下列各图中∠1的度数。
大展身手
A
B
C
D
30°
35°
40°
1
2
(4)
A
B
C
D
下图是某工厂生产的一种零件,如果三个锐角的和为135°,则说明该零件合格,工人师傅却只测量∠ADC的度数就能判断零件是否合格,你能解释其中的道理么
生活中离不开数学
E
1、如图所示,AB//CD,∠A=37°, ∠F=26°,那么∠C等于( )
F
A
B
E
C
D
A、 26°
B、 63°
C、 37°
D、 60°
课堂检测
2、如图所示,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
F
A
B
E
C
D
A、 26°
B、 63°
C、 37°
D、 60°
3、如图所示,AB//CD,AD、BC相交于O点,若∠BAD=35°, ∠BOD=76°,则∠C的度数是( )
A、 31°
B、 35°
C、 41°
D、 76°
A
B
O
C
D
小试身手
3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______
A
D
E
C
B
1
4
3
2
30°
例题解析
例题1:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
80°
70°
?
?
∵∠ADC是△ABD的外角(已知)
解:
∴∠ADC=∠B+∠BAD=80°
又∵∠B=∠BAD(已知)
(三角形的一个外角等于与它不
相邻的两个内角的和 )
∴∠B=80°×
=40°(等量代换)
课后思考
如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的
度数。
A
B
C
D
E
F
1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:______________________.
A
B
C
D
P
1
2
∠A< ∠2< ∠1
求证: ∠A<∠1
一题多变
20°
30°
51°
若∠ABP=20°, ∠ACP=30°, ∠A=51°,
求∠1的度数?
思维提升
1、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C
=180°
提高作业
1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______
1
提高作业
1、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
如图,计算∠BOC
让 我 们 一 起 去 发 现
提高作业
如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
3、如图,AD是△ABC的角平分线,E是BC延长线上一点,∠EAC=∠B, ∠ADE与∠DAE相等吗?
解:∠ADE与∠DAE相等.
因为 ∠DAE= ∠DAC+ ∠EAC,
∠ADE是△ABD的一个外角,
∠ADE=∠B+ ∠BAD
因为 ∠BAD= ∠DAC, ∠EAC= ∠B,
所以∠ADE= ∠DAE
综 合 提 高
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠BED的度数.
A
B
C
D
E
解:因为AB//CD,
所以∠ABD+∠BDC=180°,
因为BE平分∠ABD,DE平分∠BDC,所以∠EBD= ∠ABD ,
∠BDE= ∠BDC,
所以∠EBD+ ∠BDE=90°,
在△BED中, ∠EBD+ ∠BDE+∠E=180°,
所以∠BED= 180°- 90°=90°.
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
学一学
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
例题2:在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80° ∠C=30 °
(1)求∠DAE
(2)你能发现∠DAE与∠B、∠C的关系吗?
(3)若只知∠B-∠C=20°,你能求出∠DAE吗?
A
B
C
D
E
3、如果一个三角形一个外角等于和它相邻的内角的1/3,另一个内角是15°,那么第三个内角是多少度
4、已知三角形ABC三个内角之比是2:3:4,则该三角形的三个外角之比为----------
5.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
2、求下列各图中∠1的度数:
30°
60°
图1
图2
35°
120°
45°
50°
∠1=90°
∠1=85°
∠1=95°
3、如图所示,BC∥DF,∠B=63°,∠ADF=88°,求∠BAD的度数。
∠BAD=25°
63°
88°
?
综合运用
1.如图,AB∥CD ,∠A=40°,∠D=45°,
求∠1和∠2.
40°
45°
1
2
综合运用
2.如图,AB∥CD,∠A=45°, ∠C=∠E,
求∠C.
45°
说一说
本节课你的收获
课堂小结
1、三角性外角的定义
2、三角形外角的性质:
(1)三角形的一个外角等于与它不相邻 的两个内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
(3)三角形的外角和等于360°
三角形的外角
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
D
三角形的外角
画图:
画出三角形的所有外角,思考它们之间有什么关系
A
B
C
1
2
3
4
5
6
探究:
如图,△ABC中,∠A=700,∠B=600,∠ACD是△ABC的一个外角.
(1)能由∠A,∠B求出∠ACD吗
(2)思考∠ACD与∠A,∠B有什么关系
A
B
C
700
600
D
500
1300
外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
外角
相邻内角
不相邻内角
1
A
B
C
D
所以∠ACD = ∠A+∠B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
>
>
结论:三角形的一个外角大于任何一个与它不相邻的内角。
证明:因为∠A+∠B +∠1 =180
且∠ACD+∠1 =180
比较∠1 和∠2的大小:
2
1
2
1
2
P
A
B
C
D
1
2、观察下图,
比一比,看谁说的好
图(1)
(1)∠1是哪个三角形的外角?
(2)∠2是哪个三角形的外角?
∠1是△ABD的外角
∠2是△PDC的外角
例:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
1
B
2
F
3
C
D
A
E
解:因为∠BAE = ∠2+∠3
∠CBF = ∠1+∠3
∠ACD = ∠1+∠2
所以∠BAE+∠CBF+∠ACD=2(∠1 +∠2 +∠3)
因为∠1 +∠2 +∠3 = 180
所以∠BAE+∠CBF+∠ACD = 2 180 =360
结论:三角形的外角和等于360°
你还有别的证明方法吗?
解:过A作AD平行于BC
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠5
所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠5=360°
两直线平行,同位角相等
D
∠2+ ∠ 3= ∠ 4+∠5
5
判断题:
1、三角形的一个外角等于两个内角的和.( )
2、三角形的一个外角大于任何一个内角.( )
如图:D是 ABC的BC边上一点, B= BAD,
ADC=80°, BAC= 70°.
求:(1) B的度数;
(2) C的度数.
试一试
AD平分∠BAC
说出下列各图中∠1的度数。
大展身手
A
B
C
D
30°
35°
40°
1
2
(4)
A
B
C
D
下图是某工厂生产的一种零件,如果三个锐角的和为135°,则说明该零件合格,工人师傅却只测量∠ADC的度数就能判断零件是否合格,你能解释其中的道理么
生活中离不开数学
E
1、如图所示,AB//CD,∠A=37°, ∠F=26°,那么∠C等于( )
F
A
B
E
C
D
A、 26°
B、 63°
C、 37°
D、 60°
课堂检测
2、如图所示,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
F
A
B
E
C
D
A、 26°
B、 63°
C、 37°
D、 60°
3、如图所示,AB//CD,AD、BC相交于O点,若∠BAD=35°, ∠BOD=76°,则∠C的度数是( )
A、 31°
B、 35°
C、 41°
D、 76°
A
B
O
C
D
小试身手
3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______
A
D
E
C
B
1
4
3
2
30°
例题解析
例题1:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
80°
70°
?
?
∵∠ADC是△ABD的外角(已知)
解:
∴∠ADC=∠B+∠BAD=80°
又∵∠B=∠BAD(已知)
(三角形的一个外角等于与它不
相邻的两个内角的和 )
∴∠B=80°×
=40°(等量代换)
课后思考
如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的
度数。
A
B
C
D
E
F
1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:______________________.
A
B
C
D
P
1
2
∠A< ∠2< ∠1
求证: ∠A<∠1
一题多变
20°
30°
51°
若∠ABP=20°, ∠ACP=30°, ∠A=51°,
求∠1的度数?
思维提升
1、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C
=180°
提高作业
1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______
1
提高作业
1、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
如图,计算∠BOC
让 我 们 一 起 去 发 现
提高作业
如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
3、如图,AD是△ABC的角平分线,E是BC延长线上一点,∠EAC=∠B, ∠ADE与∠DAE相等吗?
解:∠ADE与∠DAE相等.
因为 ∠DAE= ∠DAC+ ∠EAC,
∠ADE是△ABD的一个外角,
∠ADE=∠B+ ∠BAD
因为 ∠BAD= ∠DAC, ∠EAC= ∠B,
所以∠ADE= ∠DAE
综 合 提 高
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠BED的度数.
A
B
C
D
E
解:因为AB//CD,
所以∠ABD+∠BDC=180°,
因为BE平分∠ABD,DE平分∠BDC,所以∠EBD= ∠ABD ,
∠BDE= ∠BDC,
所以∠EBD+ ∠BDE=90°,
在△BED中, ∠EBD+ ∠BDE+∠E=180°,
所以∠BED= 180°- 90°=90°.
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
学一学
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
例题2:在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80° ∠C=30 °
(1)求∠DAE
(2)你能发现∠DAE与∠B、∠C的关系吗?
(3)若只知∠B-∠C=20°,你能求出∠DAE吗?
A
B
C
D
E
3、如果一个三角形一个外角等于和它相邻的内角的1/3,另一个内角是15°,那么第三个内角是多少度
4、已知三角形ABC三个内角之比是2:3:4,则该三角形的三个外角之比为----------
5.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
2、求下列各图中∠1的度数:
30°
60°
图1
图2
35°
120°
45°
50°
∠1=90°
∠1=85°
∠1=95°
3、如图所示,BC∥DF,∠B=63°,∠ADF=88°,求∠BAD的度数。
∠BAD=25°
63°
88°
?
综合运用
1.如图,AB∥CD ,∠A=40°,∠D=45°,
求∠1和∠2.
40°
45°
1
2
综合运用
2.如图,AB∥CD,∠A=45°, ∠C=∠E,
求∠C.
45°
说一说
本节课你的收获
课堂小结
1、三角性外角的定义
2、三角形外角的性质:
(1)三角形的一个外角等于与它不相邻 的两个内角的和
(2)三角形的一个外角大于任何一个与它不相邻的内角
(3)三角形的外角和等于360°
