黑龙江省哈尔滨市松北区对青山镇第一中学2020-2021学年高二上学期期末考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市松北区对青山镇第一中学2020-2021学年高二上学期期末考试数学(理)试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览


文档简介
____________________________________________________________________________________________
对青山镇第一中学2020-2021学年高二上学期期末考试
(理)数学学科
本试卷分第Ⅰ卷和第Ⅱ卷两部分。共150分,考试用时120分钟。第Ⅰ卷1至2页。第Ⅱ卷 2至3页。
第Ⅰ卷
评卷人 得分
一、选择题
1.命题:“ x0∈R,x02+x0﹣1>0”的否定为( )
A. x∈R,x2+x﹣1<0 B. x∈R,x2+x﹣1≤0
C. x0 R,x02+x0﹣1=0 D. x0∈R,x02+x0﹣1≤0
2.下列有关命题的说法错误的是 ( )
A.命题“同位角相等,两直线平行”的逆否命题为:“两直线不平行,同位角不相等”
B.“若实数满足,则全为0”的否命题为真命题
C.若为假命题,则、均为假命题
D.对于命题:,则:
3.若,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.阅读右面的程序框图,则输出的S=( )
A.14 B.30 C.20 D.55
5.已知椭圆的标准方程,则椭圆的焦点坐标为( )
A., B.,
C., D.,
6.以双曲线的一个焦点为圆心,离心率为半径的圆的方程可以是( )
A. B.
C. D.
7.抛物线的准线方程是( )
A. B.
C. D.
8.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为
A. B. C. D.
9.若将一个质点随机投入如图所示的长方形中,其中,,则质点落在以为直径的半圆内的概率是( )
A. B. C. D.
10.某赛季甲、乙两名篮球运动员每场比赛得分如图所示,则甲、乙两运动员得分的中位数分别是( )
A.26 33.5 B.26 36 C.23 31 D.24.5 33.5
11.下表是某厂月份用水量(单位:百吨)的一组数据:
月份 1 2 3 4
用水量 4.5 4 3 2.5
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归直线方程是,则等于( )
A.10.5 B.5.15
C.5.2 D.5.25
12.已知=(1,2,-2),=(-2,-4,4),则和( )
A.平行 B. 相交 C.垂直 D.以上都不对
评卷人 得分
二、填空题
13.命题“,”的否定为 .
14.“x>1”是“x2>x”的 条件.
15.该程序运行后输出的结果为_____
16.抛物线上一点到焦点的距离为5,则点的横坐标为________,
评卷人 得分
三、解答题
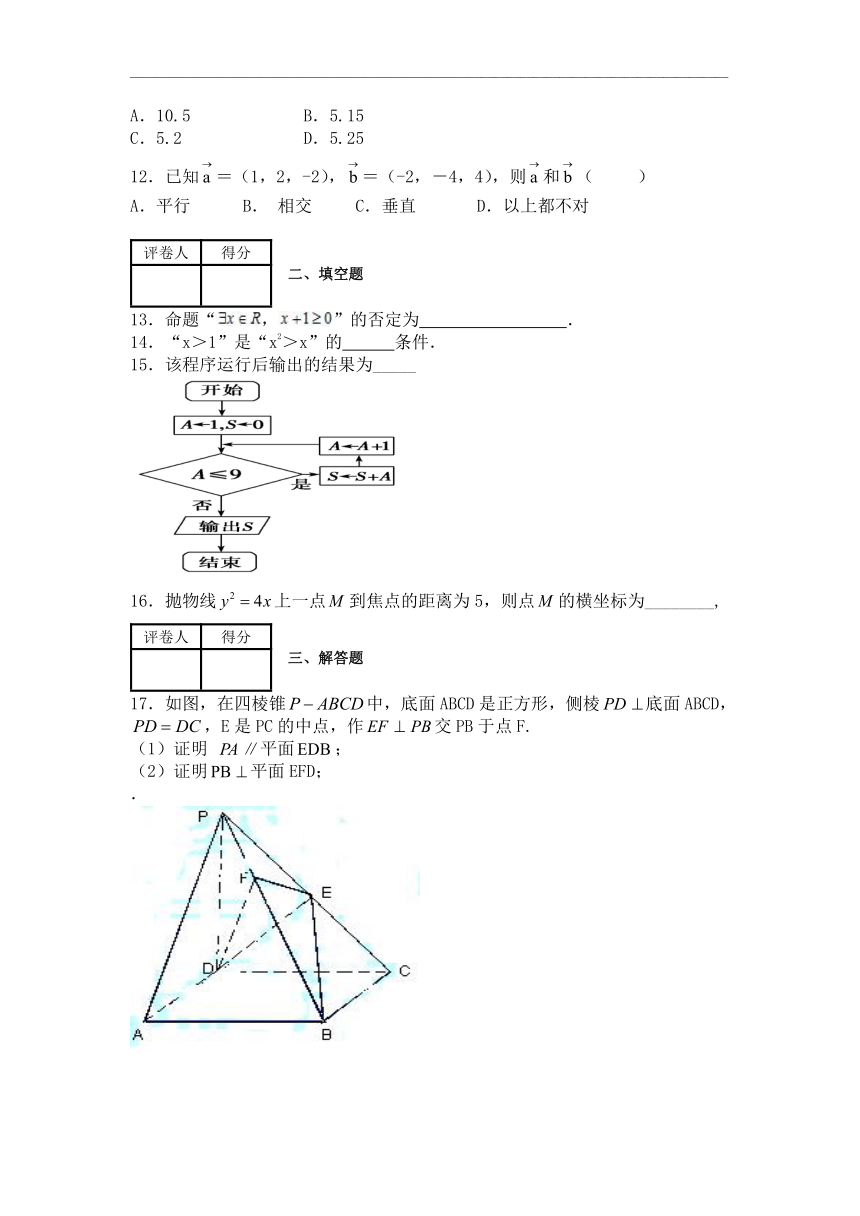
17.如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.
(1)证明 平面;
(2)证明平面EFD;
.
18.已知椭圆的中心在原点,焦点在轴上,长轴长为,且点在椭圆上.
(1)求椭圆的方程;
(2)若点P在第二象限,∠F2PF1=60°,求△PF1F2的面积.
19.已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,
(1)求的取值.
(2)比较甲、乙两组数据的稳定性,并说明理由.
注:方差公式
20.已知集合,q:,并且是的充分条件,求的取值范围.
21.长方体中,
(1)求直线所成角;
(2)求直线所成角的正弦.
22.已知函数是定义在R上的偶函数,且当≤0时,.
(1)现已画出函数在y轴左侧的图像,如图所示,请补出完整函数的图像,并根据图像写出函数的增区间;
(2)写出函数的解析式和值域.
参考答案
1.B
2.C
3. B
4.B
5.C
6.D
7.D
8.D
9.C
10.A
11.D
12.A
13.
14.充分不必要
15.45
16.
17.
(1)略 (2)略 (3)
解:如图所示建立空间直角坐标系,D为坐标原点.设(1)证明:连结AC,AC交BD于G.连结EG.
依题意得底面ABCD是正方形, 是此正方形的中心,
故点G的坐标为且. 这表明.而平面EDB且平面EDB,平面EDB。
(2)证明:依题意得。又故 , 由已知,且所以平面EFD.
(3)解:设点F的坐标为则
从而所以
由条件知,即 解得 。
点F的坐标为 且
,即,故是二面角的平面角.
∵且
,所以,二面角C—PC—D的大小为
18.(1);(2).
19.(1)m=3, n=8(2)乙组数据的稳定性强
20.
21.(1)直线所成角为90°;(2) 。
22.(1)(-1,0),(1,+∞)(2)值域为
对青山镇第一中学2020-2021学年高二上学期期末考试
(理)数学学科
本试卷分第Ⅰ卷和第Ⅱ卷两部分。共150分,考试用时120分钟。第Ⅰ卷1至2页。第Ⅱ卷 2至3页。
第Ⅰ卷
评卷人 得分
一、选择题
1.命题:“ x0∈R,x02+x0﹣1>0”的否定为( )
A. x∈R,x2+x﹣1<0 B. x∈R,x2+x﹣1≤0
C. x0 R,x02+x0﹣1=0 D. x0∈R,x02+x0﹣1≤0
2.下列有关命题的说法错误的是 ( )
A.命题“同位角相等,两直线平行”的逆否命题为:“两直线不平行,同位角不相等”
B.“若实数满足,则全为0”的否命题为真命题
C.若为假命题,则、均为假命题
D.对于命题:,则:
3.若,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.阅读右面的程序框图,则输出的S=( )
A.14 B.30 C.20 D.55
5.已知椭圆的标准方程,则椭圆的焦点坐标为( )
A., B.,
C., D.,
6.以双曲线的一个焦点为圆心,离心率为半径的圆的方程可以是( )
A. B.
C. D.
7.抛物线的准线方程是( )
A. B.
C. D.
8.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为
A. B. C. D.
9.若将一个质点随机投入如图所示的长方形中,其中,,则质点落在以为直径的半圆内的概率是( )
A. B. C. D.
10.某赛季甲、乙两名篮球运动员每场比赛得分如图所示,则甲、乙两运动员得分的中位数分别是( )
A.26 33.5 B.26 36 C.23 31 D.24.5 33.5
11.下表是某厂月份用水量(单位:百吨)的一组数据:
月份 1 2 3 4
用水量 4.5 4 3 2.5
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归直线方程是,则等于( )
A.10.5 B.5.15
C.5.2 D.5.25
12.已知=(1,2,-2),=(-2,-4,4),则和( )
A.平行 B. 相交 C.垂直 D.以上都不对
评卷人 得分
二、填空题
13.命题“,”的否定为 .
14.“x>1”是“x2>x”的 条件.
15.该程序运行后输出的结果为_____
16.抛物线上一点到焦点的距离为5,则点的横坐标为________,
评卷人 得分
三、解答题
17.如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.
(1)证明 平面;
(2)证明平面EFD;
.
18.已知椭圆的中心在原点,焦点在轴上,长轴长为,且点在椭圆上.
(1)求椭圆的方程;
(2)若点P在第二象限,∠F2PF1=60°,求△PF1F2的面积.
19.已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,
(1)求的取值.
(2)比较甲、乙两组数据的稳定性,并说明理由.
注:方差公式
20.已知集合,q:,并且是的充分条件,求的取值范围.
21.长方体中,
(1)求直线所成角;
(2)求直线所成角的正弦.
22.已知函数是定义在R上的偶函数,且当≤0时,.
(1)现已画出函数在y轴左侧的图像,如图所示,请补出完整函数的图像,并根据图像写出函数的增区间;
(2)写出函数的解析式和值域.
参考答案
1.B
2.C
3. B
4.B
5.C
6.D
7.D
8.D
9.C
10.A
11.D
12.A
13.
14.充分不必要
15.45
16.
17.
(1)略 (2)略 (3)
解:如图所示建立空间直角坐标系,D为坐标原点.设(1)证明:连结AC,AC交BD于G.连结EG.
依题意得底面ABCD是正方形, 是此正方形的中心,
故点G的坐标为且. 这表明.而平面EDB且平面EDB,平面EDB。
(2)证明:依题意得。又故 , 由已知,且所以平面EFD.
(3)解:设点F的坐标为则
从而所以
由条件知,即 解得 。
点F的坐标为 且
,即,故是二面角的平面角.
∵且
,所以,二面角C—PC—D的大小为
18.(1);(2).
19.(1)m=3, n=8(2)乙组数据的稳定性强
20.
21.(1)直线所成角为90°;(2) 。
22.(1)(-1,0),(1,+∞)(2)值域为
同课章节目录
