[双减-同步分层作业]北师大七上 3.5 探索与表达规律(汉答案)
文档属性
| 名称 | [双减-同步分层作业]北师大七上 3.5 探索与表达规律(汉答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 574.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 16:05:56 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
一、学习目标 1、探索数量关系,应用符号语言结合图形语言表示规律,通过验算证明规律。2、数的变化规律。
二、夯实基础 1、通过探索数量关系,运用符号表示规律,运算验证规律的过程,使学生进一步理解掌握探索规律的步骤。2、会用代数式表示简单问题中的数量关系,在探究的过程中培养学生的观察能力,数学概括与表达能力以及创新能力。
三、能力提升 通过活动,为学生创设生动活泼的探究知识的情境,从而调动学生学习数学知识的积极性,使学生有自主地发现知识,创造性地解决问题。培养学生创新能力,应用意识。
双减-同步分层作业 3.5 探索与表达规律
学习目标+知识梳理
学习目标
1、探索数量关系,应用符号语言结合图形语言表示规律,通过验算证明规律。
2、数的变化规律。
3、通过各种途径,培养学生的搜索力、发现力、概括力、想象力、记忆力、思维力、操作力、应变力、创造力和自我调控力。
知识梳理
按规律写答案 1 3 5 7 9 11........... 第100个数字是多少 第n个数字的表达式是
找出一列数2,3,5,8,13,( ),34的规律,在( )里的数应为( )。
3、一首永远唱不完的儿歌,你能用字母表示这首儿歌吗?
1只青蛙,1张嘴,2只眼睛,4条腿,1声扑通跳下水。
2只青蛙,2张嘴,4只眼睛,8条腿,2声扑通跳下水。
3只青蛙,3张嘴,6只眼睛,12条腿,3声扑通跳下水。
……
a只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水。
4、小时侯我们都玩过搭火柴棒的游戏,今天我们不妨重拾童年趣事,利用手中的火柴棒搭建一些常见的图形,探索规律。
⑴填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
⑵照这样的规律搭建下去,搭n个这样的三角形需要多少根火柴棒?
夯实基础(必做题)
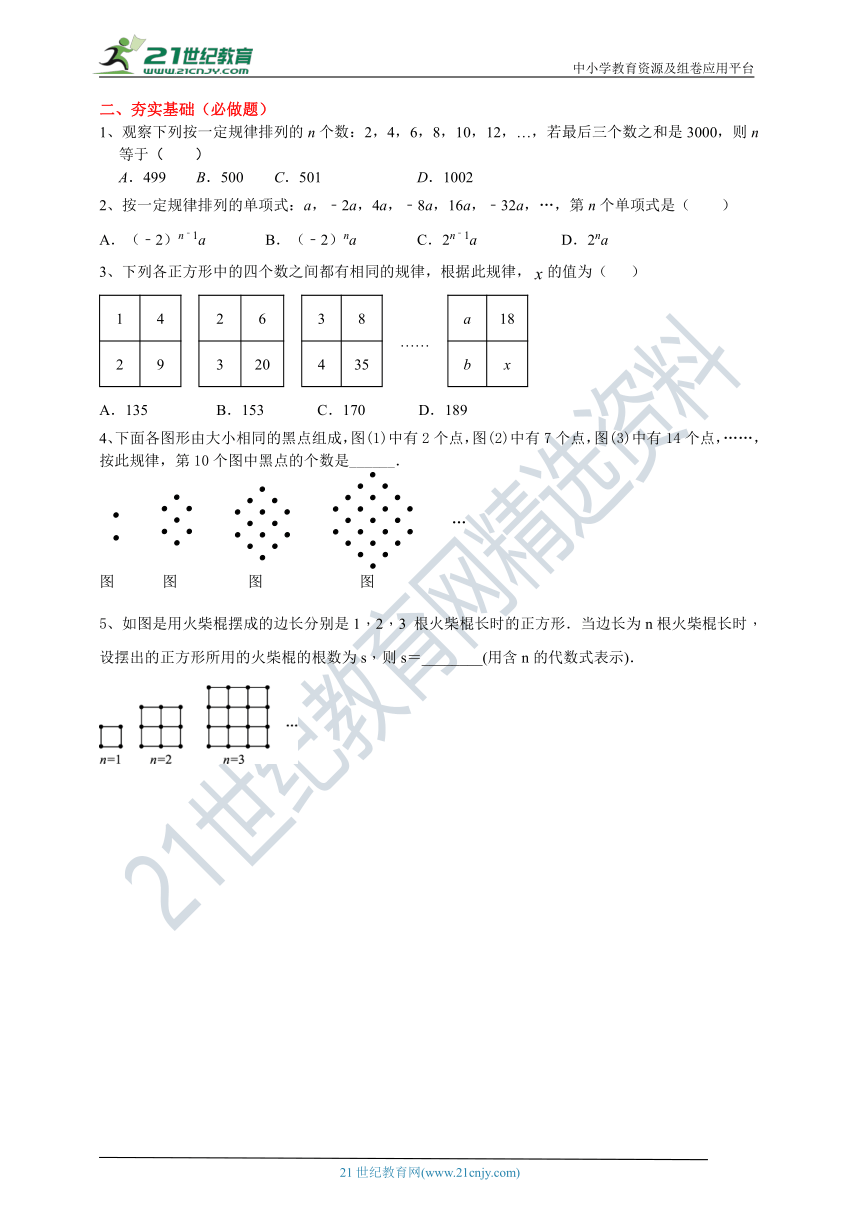
1、观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是3000,则n等于( )
A.499 B.500 C.501 D.1002
2、按一定规律排列的单项式:a,﹣2a,4a,﹣8a,16a,﹣32a,…,第n个单项式是( )
A.(﹣2)n﹣1a B.(﹣2)na C.2n﹣1a D.2na
3、下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
1 4
2 9
26320 38435 …… a18bx
A.135 B.153 C.170 D.189
4、下面各图形由大小相同的黑点组成,图(1)中有2个点,图(2)中有7个点,图(3)中有14个点,……,按此规律,第10个图中黑点的个数是______.
5、如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍长时的正方形.当边长为n根火柴棍长时,设摆出的正方形所用的火柴棍的根数为s,则s=________(用含n的代数式表示).
能力提升(选做题)
1、某校生物教师李老师在生物试验室做试验时,将水稻种子分组进行发芽试验.第1组取3粒,第2组取5粒,第3组取7粒,…,即每组所取种子数目比该组的前一组增加2粒,按此规律,请你推测第n组应取种子数为( )
A (2n+1)粒 B (2n-1)粒 C 2n粒 D (n+2)粒
2、填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
3、观察下列图形,则第n个图形中三角形的个数是( )
A.2n+2 B.4n+4 C.4n﹣4 D.4n
4、下面是按照一定规律画出的“树形图”,经观察可以发现:图2比图1多出2个“树枝”,图3比图2多出4个“树枝”,图4比图3多出8个“树枝”,…,照此规律,图6比图2多出( )个“树枝”.
A.60 B.32 C.16 D.64
5、例 计算:
解:
==.
观察上面的解题过程,请你用类似的方法计算:
6、欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:
____________________________.
7、将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图)。
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由。
参考答案
一、
1、199 2n-1
2、21
3、a只青蛙, n 张嘴, 2n只眼睛, 4n 条腿, n 声扑通跳下水。
4、
三角形个数 1 2 3 4 5
火柴棒根数 3 5 7 9 11
搭n个这样的三角形需要2n+1根火柴棒
二、
C 2、A 3、C 4、119 5、2n(n+1)
三、
A 2、D 3、D 4、A
5、解:由题得:
原式=
=
=
6、(1)填表如下:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8 6
棱数E 6 9 12 12
面数F 4 5 6 8
(2)据上表中的数据规律发现,多面体的顶点数V、棱数E、面数F之间存在关系式:V+F-E=2.
7、解:(1)从表格知道中间的数为a,上面的为a﹣12,下面的为a+12,左面的为a﹣2,右面的为a+2,a+(a﹣2)+(a+2)+(a﹣12)+(a+12)=5a.
(2)令5a=2020,a=404,所以可以,5个数分别是392、402、404、406、416.
(3)令5a=365,a=73,所以可以,5个数分别是61、71、73、75、85.
…
图(1)
图(4)
图(3)
图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
一、学习目标 1、探索数量关系,应用符号语言结合图形语言表示规律,通过验算证明规律。2、数的变化规律。
二、夯实基础 1、通过探索数量关系,运用符号表示规律,运算验证规律的过程,使学生进一步理解掌握探索规律的步骤。2、会用代数式表示简单问题中的数量关系,在探究的过程中培养学生的观察能力,数学概括与表达能力以及创新能力。
三、能力提升 通过活动,为学生创设生动活泼的探究知识的情境,从而调动学生学习数学知识的积极性,使学生有自主地发现知识,创造性地解决问题。培养学生创新能力,应用意识。
双减-同步分层作业 3.5 探索与表达规律
学习目标+知识梳理
学习目标
1、探索数量关系,应用符号语言结合图形语言表示规律,通过验算证明规律。
2、数的变化规律。
3、通过各种途径,培养学生的搜索力、发现力、概括力、想象力、记忆力、思维力、操作力、应变力、创造力和自我调控力。
知识梳理
按规律写答案 1 3 5 7 9 11........... 第100个数字是多少 第n个数字的表达式是
找出一列数2,3,5,8,13,( ),34的规律,在( )里的数应为( )。
3、一首永远唱不完的儿歌,你能用字母表示这首儿歌吗?
1只青蛙,1张嘴,2只眼睛,4条腿,1声扑通跳下水。
2只青蛙,2张嘴,4只眼睛,8条腿,2声扑通跳下水。
3只青蛙,3张嘴,6只眼睛,12条腿,3声扑通跳下水。
……
a只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水。
4、小时侯我们都玩过搭火柴棒的游戏,今天我们不妨重拾童年趣事,利用手中的火柴棒搭建一些常见的图形,探索规律。
⑴填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
⑵照这样的规律搭建下去,搭n个这样的三角形需要多少根火柴棒?
夯实基础(必做题)
1、观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是3000,则n等于( )
A.499 B.500 C.501 D.1002
2、按一定规律排列的单项式:a,﹣2a,4a,﹣8a,16a,﹣32a,…,第n个单项式是( )
A.(﹣2)n﹣1a B.(﹣2)na C.2n﹣1a D.2na
3、下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
1 4
2 9
26320 38435 …… a18bx
A.135 B.153 C.170 D.189
4、下面各图形由大小相同的黑点组成,图(1)中有2个点,图(2)中有7个点,图(3)中有14个点,……,按此规律,第10个图中黑点的个数是______.
5、如图是用火柴棍摆成的边长分别是1,2,3 根火柴棍长时的正方形.当边长为n根火柴棍长时,设摆出的正方形所用的火柴棍的根数为s,则s=________(用含n的代数式表示).
能力提升(选做题)
1、某校生物教师李老师在生物试验室做试验时,将水稻种子分组进行发芽试验.第1组取3粒,第2组取5粒,第3组取7粒,…,即每组所取种子数目比该组的前一组增加2粒,按此规律,请你推测第n组应取种子数为( )
A (2n+1)粒 B (2n-1)粒 C 2n粒 D (n+2)粒
2、填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
3、观察下列图形,则第n个图形中三角形的个数是( )
A.2n+2 B.4n+4 C.4n﹣4 D.4n
4、下面是按照一定规律画出的“树形图”,经观察可以发现:图2比图1多出2个“树枝”,图3比图2多出4个“树枝”,图4比图3多出8个“树枝”,…,照此规律,图6比图2多出( )个“树枝”.
A.60 B.32 C.16 D.64
5、例 计算:
解:
==.
观察上面的解题过程,请你用类似的方法计算:
6、欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:
____________________________.
7、将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图)。
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由。
参考答案
一、
1、199 2n-1
2、21
3、a只青蛙, n 张嘴, 2n只眼睛, 4n 条腿, n 声扑通跳下水。
4、
三角形个数 1 2 3 4 5
火柴棒根数 3 5 7 9 11
搭n个这样的三角形需要2n+1根火柴棒
二、
C 2、A 3、C 4、119 5、2n(n+1)
三、
A 2、D 3、D 4、A
5、解:由题得:
原式=
=
=
6、(1)填表如下:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8 6
棱数E 6 9 12 12
面数F 4 5 6 8
(2)据上表中的数据规律发现,多面体的顶点数V、棱数E、面数F之间存在关系式:V+F-E=2.
7、解:(1)从表格知道中间的数为a,上面的为a﹣12,下面的为a+12,左面的为a﹣2,右面的为a+2,a+(a﹣2)+(a+2)+(a﹣12)+(a+12)=5a.
(2)令5a=2020,a=404,所以可以,5个数分别是392、402、404、406、416.
(3)令5a=365,a=73,所以可以,5个数分别是61、71、73、75、85.
…
图(1)
图(4)
图(3)
图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
