1.3 三角函数的诱导公式-人教A版高中数学必修四讲义(解析版)
文档属性
| 名称 | 1.3 三角函数的诱导公式-人教A版高中数学必修四讲义(解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 318.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览




文档简介
教材要点 学科素养 学考 高考 考法指津 高考考向
1.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1 1.熟练掌握相应角的终边上点的坐标的特点。 2.使用诱导公式的目的在于将任意角的三角函数转化为锐角的三角函数。 【考查内容】诱导公式的应用,三角函数的基本关系式。 【考查题型】选择题、填空题 【分值情况】5分
2.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平 1
3.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1
4.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1
高中数学,同步讲义 必修四 第一章 三角函数 第三讲 三角函数的诱导公式
知识点一 诱导公式一
设角α的终边与单位圆的交点为P,由三角函数定义知P点坐标为(cos α,sin α).
思考 角π+α的终边与角α的终边有什么关系?角π+α的终边与单位圆的交点P1(cos(π+α),sin(π+α))与点P(cos α,sin α)呢?它们的三角函数之间有什么关系?
答案 角π+α的终边与角α的终边关于原点对称,P1与P也关于原点对称,它们的三角函数关系如下:
诱导公式一
sinπ+α=-sin α, cosπ+α=-cos α, tanπ+α=tan α.
知识点二 诱导公式二
思考 角-α的终边与角α的终边有什么关系?角-α的终边与单位圆的交点P2(cos(-α),sin(-α))与点P(cos α,sin α)有怎样的关系?它们的三角函数之间有什么关系?
答案 角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称,它们的三角函数关系如下:
诱导公式二
sin-α=-sin α, cos-α=cos α, tan-α=-tan α.
知识点三 诱导公式三
思考 角π-α的终边与角α的终边有什么关系?角π-α的终边与单位圆的交点P3(cos(π-α),sin(π-α))与点P(cos α,sin α)有怎样的关系?它们的三角函数之间有什么关系?
答案 角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称,它们的三角函数关系如下:
诱导公式三
sin(π-α)=sin α, cos(π-α)=-cos α, tan(π-α)=-tan α.
梳理 公式一~三都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数之间的关系,这三组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.
知识点四 诱导公式四
完成下表,并由此总结角α,角-α的三角函数值间的关系.
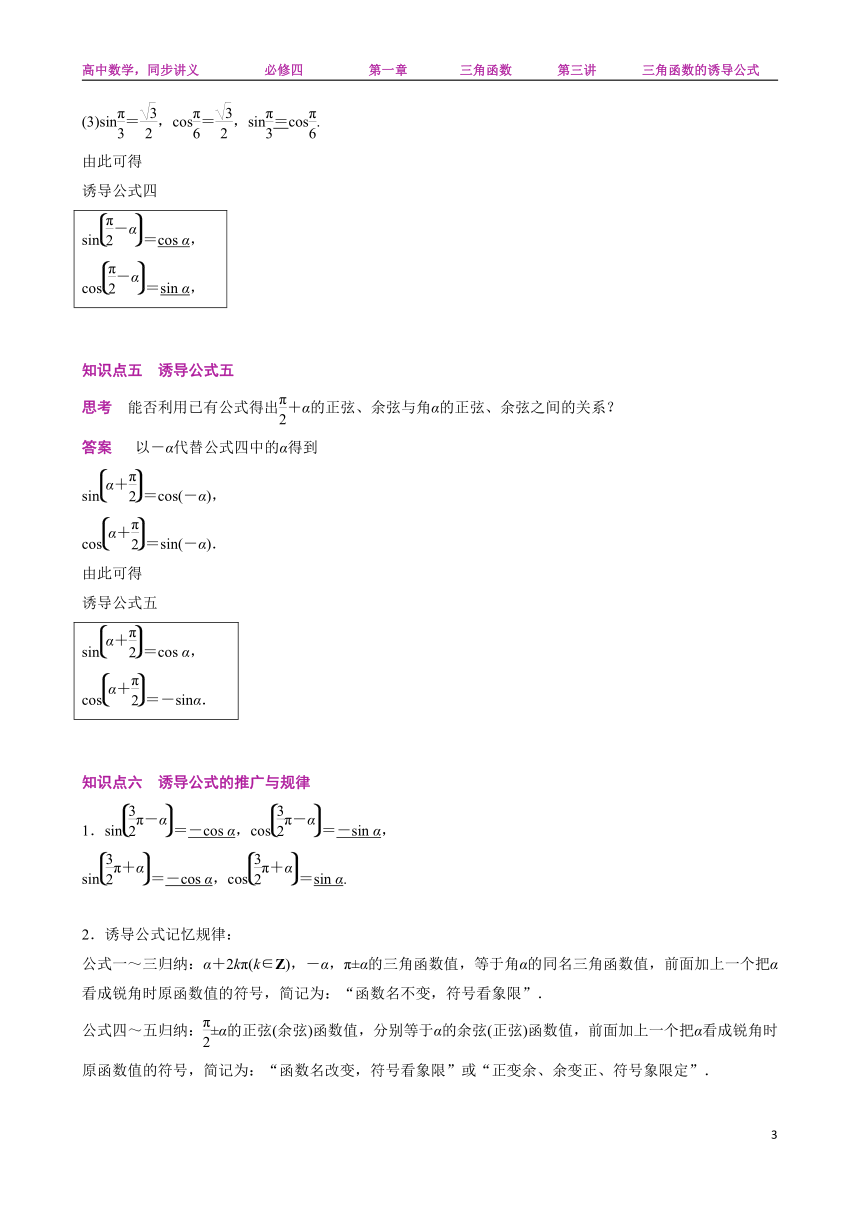
(1)sin=,cos=,sin=cos;
(2)sin=,cos=,sin=cos;
(3)sin=,cos=,sin=cos.
由此可得
诱导公式四
sin=cos α, cos=sin α,
知识点五 诱导公式五
思考 能否利用已有公式得出+α的正弦、余弦与角α的正弦、余弦之间的关系?
答案 以-α代替公式四中的α得到
sin=cos(-α),
cos=sin(-α).
由此可得
诱导公式五
sin=cos α, cos=-sinα.
知识点六 诱导公式的推广与规律
1.sin=-cos α,cos=-sin α,
sin=-cos α,cos=sin α.
2.诱导公式记忆规律:
公式一~三归纳:α+2kπ(k∈Z),-α,π±α的三角函数值,等于角α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名不变,符号看象限”.
公式四~五归纳:±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名改变,符号看象限”或“正变余、余变正、符号象限定”.
五组诱导公式可以统一概括为“k·±α(k∈Z)”的诱导公式.
记忆口诀:奇变偶不变,符号看象限.其中“奇、偶”是指k·±α(k∈Z)中k的奇偶性,当k为奇数时,正弦变余弦,余弦变正弦;当k为偶数时,函数名不变.“符号”看的应该是诱导公式中,把α看成锐角时原函数值的符号,而不是α函数值的符号.
题型一 利用诱导公式求值
命题角度1 给角求值问题
例1-1 求下列各三角函数值:
(1)sin;(2)cos;(3)tan(-855°).
解析:(1)sin=sin=sinπ
=sin=-sin=-.
(2)cos=cos=cosπ=cos
=-cos=-.
(3)tan(-855°)=tan(-3×360°+225°)
=tan225°=tan(180°+45°)=tan45°=1.
变式训练1-1 求下列各三角函数式的值:
(1)sin 1 320°;(2)cos;(3)tan(-945°).
解析: (1) sin 1 320°=sin(3×360°+240°)
=sin 240°=sin(180°+60°)=-sin 60°=-.
(2) cos=cos
=cos=-cos=-.
(3)tan(-945°)=-tan 945°=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)=-tan 45°=-1.
命题角度2 给值求值或给值求角问题
例1-2 (1)已知sin(π+θ)=-cos(2π-θ),|θ|<,则θ等于( )
A.- B.- C. D.
答案 D
解析: 由sin(π+θ)=-cos(2π-θ),|θ|<,
可得-sin θ=-cos θ,|θ|<,
即tan θ=,|θ|<,∴θ=.
(2)已知cos=,求cos-sin2的值.
解析: 因为cos=cos
=-cos=-,
sin2=sin2=1-cos2
=1-2=,
所以cos-sin2=--=-.
变式训练1-2 已知sin β=,cos(α+β)=-1,则sin(α+2β)的值为( )
A.1 B.-1 C. D.-
解析: 由cos(α+β)=-1,得α+β=2kπ+π(k∈Z),
则α+2β=(α+β)+β=2kπ+π+β(k∈Z),
sin(α+2β)=sin(2kπ+π+β)=sin(π+β)
=-sin β=-.
答案 D
题型二 利用诱导公式化简
例2 已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且sin(α-π)=,
求f(α)的值;
(3)若α=-,求f(α)的值.
解析: (1)f(α)==-cos α.
(2)∵sin(α-π)=-sin α=,
∴sin α=-.又α是第三象限角,
∴cos α=-.∴f(α)=.
(3)∵-=-6×2π+,
∴f=-cos
=-cos
=-cos
=-.
变式训练2 化简:
·sin(α-2π)·cos(2π-α).
解析: 原式=·[-sin(2π-α)]·cos(2π-α)
=·sin α·cos α
=cos2α.
题型三 利用诱导公式求值
例3、 已知cos=,≤α≤,
求sin的值.
解析: ∵α+=+,
∴sin=sin=cos=.
变式训练3
已知sin=,求cos的值.
解析: ∵+α+-α=,
∴-α=-.
∴cos=cos
=sin=.
题型四 利用诱导公式证明三角恒等式
规律方法
例4、
求证:=-tan α.
证明: ∵左边=
=
=
==-
=-tan α=右边.
∴原等式成立.
变式训练4
求证:=.
证明: 右边=
=
=
=
===左边,
所以原等式成立.
题型五 诱导公式的综合应用
规律方法
例5 已知f(α)=.
(1)化简f(α);
(2)若角A是△ABC的内角,且f(A)=,
求tan A-sin A的值.
解析: (1)f(α)==cos α.
(2)因为f(A)=cos A=,
又A为△ABC的内角,
所以由平方关系,得sin A==,
所以tan A==,
所以tan A-sin A=-=.
变式训练5
已知f(α)=.
(1)化简f(α);
(2)若f=-,且α是第二象限角,求tan α.
解析:
(1)f(α)=
==sin α.
(2)由sin=-,得cos α=-,
又α是第二象限角,所以sin α==,
则tan α==-.
一、选择题
1.已知tan α=4,则tan(π-α)等于( )
A.π-4 B.4 C.-4 D.4-π
解析: tan(π-α)=-tan α=-4.
答案 C
2.cos(π+x)等于( )
A.cos x B.-cos x
C.sin x D.-sin x
解析: 由诱导公式得cos(π+x)=-cos x.
答案 B
3.已知sin(π+α)=,且α是第四象限角,则cos(α-2π)的值是( )
A.- B. C.- D.
解析: 因为sin(π+α)=,且sin(π+α)=-sin α,
所以sin α=-,
又因为α是第四象限角,
所以cos(α-2π)=cos α=
==.
答案 B
4.记cos(-80°)=k,那么tan 100°等于( )
A. B.-
C. D.-
解析: ∵cos(-80°)=k,∴cos 80°=k,
∴sin 80°=,则tan 80°=.
∴tan 100°=-tan 80°=-.
答案 B
5.若sin(π-α)=log8,且α∈,则cos(π+α)的值为( )
A. B.-
C.± D.以上都不对
解析: ∵sin(π-α)=sin α=2-2=-,
α∈,
∴cos(π+α)=-cos α=-
=- =-.
答案 B
6.若cos(2π-α)=,则sin等于( )
A.- B.-
C. D.±
解析: ∵cos(2π-α)=cos(-α)=cos α=,
∴sin=-cos α=-.
答案 A
7.已知tan θ=2,则等于( )
A.2 B.-2 C.0 D.
解析: =
===-2.
答案 B
8.已知sin=,那么cos α等于( )
A.- B.-
C. D.
解析: sin=cos α,故cos α=,故选C.
答案 C
9.已知sin 10°=k,则cos 620°的值为( )
A.k B.-k C.±k D.不确定
解析: cos 620°=cos(360°+260°)=cos 260°=cos(270°-10°)=-sin 10°=-k
答案 B.
10.若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos C B.sin(A+B)=-sin C
C.cos=sin B D.sin=cos
解析: ∵A+B+C=π,∴A+B=π-C,
∴cos(A+B)=-cos C,sin(A+B)=sin C,故A,B项不正确;
∵A+C=π-B,∴=,
∴cos=cos=sin,故C项不正确;
∵B+C=π-A,
∴sin=sin=cos,故D项正确.
答案 D
二、填空题
11.已知600°角的终边上有一点P(a,-3),则a的值为______.
解析: tan 600°=tan(360°+240°)=tan(180°+60°)
=tan 60°=-=,即a=-.
答案 -
12. 的值是________.
解析: 原式=
=
=
===-2.
答案 -2
13.已知a=tan,b=cos ,c=sin,则a,b,c的大小关系是________.
解析: ∵a=-tan=-tan =-,
b=cos=cos =,
c=-sin=-sin=-,
∴b>a>c.
答案 b>a>c
14.化简= .
解析: 原式=
==-1.
答案 -1
三、解答题
15.求下列三角函数值.
(1)tanπ+cos(-1 650°)+sinπ;
(2)7cos270°+3sin270°+tan765°.
解析:(1)原式=tan+cos1650°+sin
=-tan+cos(4×360°+210°)-sin
=-1+cos210°-
=-1+cos(180°+30°)-
=--cos30°
=--.
(2)原式=7cos(180°+90°)+3sin(180°+90°)+tan(2×360°+45°)
=-7cos90°-3sin90°+tan45°
=-2.
16.化简下列各式:
(1);
(2).
解析: (1)原式=
=
=1.
(2)原式=
=
==.
17.已知角α的终边经过单位圆上的点P.
(1)求sin α的值;
(2)求·的值.
解析: (1)∵点P在单位圆上,
∴由正弦的定义得sin α=-.
(2)原式=·==,
由余弦的定义得cos α=,
故原式=.
一、选择题
1.已知sin=,则sin的值为( )
A. B.- C. D.-
解析: sin=sin
=sin=.
答案 C
2.化简sin2(π+α)-cos(π+α)·cos(-α)+1的值为( )
A.1 B.2sin2α C.0 D.2
解析: 原式=(-sin α)2-(-cos α)·cos α+1=sin2α+cos2α+1=2.
答案 D
3.已知n为整数,化简所得的结果是( )
A.tan nα B.-tan nα
C.tan α D.-tan α
解析: 当n=2k,k∈Z时,=
==tan α;
当n=2k+1,k∈Z时,=
===tan α.故选C.
答案 C
4.已知sin=,则cos的值为( )
A. B.- C. D.-
解析: cos=cos
=sin=.
答案 C
5.化简sin·cos·tan的结果是( )
A.1 B.sin2α C.-cos2α D.-1
解析: 因为sin=cos α,
cos=cos=-sin α,
tan==,
所以原式=cos α(-sin α)=-cos2α,故选C.
答案 C
6.已知f(sin x)=cos 3x,则f(cos 10°)的值为( )
A.- B. C.- D.
解析: f(cos 10°)=f(sin 80°)=cos 240°
=cos(180°+60°)=-cos 60°=-.
答案 A
7.若sin(π+α)+cos=-m,则cos+2sin(2π-α)的值为( )
A.- B. C.- D.
解析: ∵sin(π+α)+cos=-sin α-sin α=-m,∴sin α=.
故cos+2sin(2π-α)=-sin α-2sin α
=-3sin α=-.
答案 C
8.下列式子中正确的是( )
A.sin(π-α)=-sinα
B.cos(π+α)=cosα
C.cosα=sinα
D.sin(2π+α)=sinα
解析:对于选项A,令α=,得sin(π-α)=sin=1≠-sin,所以A错误;
对于选项B,令α=0,得cos(π+α)=cosπ=-1≠cos0,所以B错误;
对于选项C,令α=0,得cosα=cos0=1≠sin0,所以C错误.
答案 D
9.已知函数f(x)=asin(πx+α)+bcos(πx+β)+4,x∈R,且f(2017)=3,则f(2018)的值为( )
A.3 B.4
C.5 D.6
解析:∵f(2017)=asin(2017π+α)+bcos(2017π+β)+4=3,
∴asin(2017π+α)+bcos(2017π+β)=-1,
∴f(2018)=asin(2017π+α+π)+bcos(2017π+β+π)+4
=-asin(2017π+α)-bcos(2017π+β)+4=1+4=5.
答案 C
10.计算sin21°+sin22°+sin23°+…+sin289°=( )
A.89 B.90
C. D.45
解析:
原式=sin21°+sin22°+sin23°+…+sin244°+sin245°+sin2(90°-44°)+…+sin2(90°-3°)
+sin2(90°-2°)+sin2(90°-1°)
=sin21°+sin22°+sin23°+…+sin244°+sin245°+cos244°+…+cos23°+cos22°+cos21°
=(sin21°+cos21°)+(sin22°+cos22°)+(sin23°+cos23°)+…+(sin244°+cos244°)+sin245°
=44+
=.
答案 C
二、填空题
11.化简=________.
解析: =
===1.
答案 1
12.设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β为非零常数,若f(2 017)=-1,则f(2 018)=________.
解析: ∵f(2 018)=asin(2 018π+α)+bcos(2 018π+β)
=asin(π+2 017π+α)+bcos(π+2 017π+β)
=-asin(2 017π+α)-bcos(2 017π+β)
=-f(2 017),
又f(2 017)=-1,∴f(2 018)=1.
答案 1
13.已知f(x)=则f+f的值为________.
解析: 因为f=sin
=sin=sin=;
f=f-1=f-2
=sin-2=--2=-,
所以f+f=-2.
答案 -2
14.给出下列三个结论,其中正确结论的序号是 .
①sin(π+α)=-sin α成立的条件是角α是锐角;
②若cos(nπ-α)=(n∈Z),则cos α=;
③若α≠(k∈Z),则tan=.
解析: 由诱导公式二,知α∈R时,sin(π+α)=-sin α,所以①错误.
当n=2k(k∈Z)时,cos(nπ-α)=cos(-α)=cos α,此时cos α=,
当n=2k+1(k∈Z)时,cos(nπ-α)=cos[(2k+1)π-α]=cos(π-α)=-cos α,此时cos α=-,所以②错误.
若α≠(k∈Z),则tan===-,所以③正确.
答案 ③
三、解答题
15. 化简下列各式:
(1);
(2).
解析: (1)原式=
==-=-tan α.
(2)原式=
==
==-1.
16.已知sin(5π-θ)+sin=,求sin4+cos4的值.
解析: ∵sin(5π-θ)+sin
=sin(π-θ)+sin
=sin θ+cos θ=,
∴sin θcos θ=[(sin θ+cos θ)2-1]
=×=,
∴sin4+cos4=cos4θ+sin4θ
=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-2×2=.
17.已知α是第四象限角,且f(α)=.
(1)若cos=,求f(α)的值;
(2)若α=-1 860°,求f(α)的值.
解析: f(α)=
==.
(1)∵cos=,
∴cos=,
∴cos=,
∴sin α=-,∴f(α)==-5.
(2)当α=-1 860°时,f(α)=
==
==
=-.
18.是否存在角α,β,α∈,β∈(0,π),使等式sin(3π-α)=cos,
cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
解析:假设存在角α,β满足条件,
则
①2+②2,得sin2α+3cos2α=2.
∴cos2α=,∴cosα=±.
∵α∈,∴cosα=.
由cosα=,cosα=cosβ,
得cosβ=.∵β∈(0,π),∴β=,
∴sinβ=,结合①可知sinα=,
则α=.
故存在α=,β=满足条件.
1.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1 1.熟练掌握相应角的终边上点的坐标的特点。 2.使用诱导公式的目的在于将任意角的三角函数转化为锐角的三角函数。 【考查内容】诱导公式的应用,三角函数的基本关系式。 【考查题型】选择题、填空题 【分值情况】5分
2.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平 1
3.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1
4.与的正弦、余弦、正切值的关系 数学抽象 水平1 水平1
高中数学,同步讲义 必修四 第一章 三角函数 第三讲 三角函数的诱导公式
知识点一 诱导公式一
设角α的终边与单位圆的交点为P,由三角函数定义知P点坐标为(cos α,sin α).
思考 角π+α的终边与角α的终边有什么关系?角π+α的终边与单位圆的交点P1(cos(π+α),sin(π+α))与点P(cos α,sin α)呢?它们的三角函数之间有什么关系?
答案 角π+α的终边与角α的终边关于原点对称,P1与P也关于原点对称,它们的三角函数关系如下:
诱导公式一
sinπ+α=-sin α, cosπ+α=-cos α, tanπ+α=tan α.
知识点二 诱导公式二
思考 角-α的终边与角α的终边有什么关系?角-α的终边与单位圆的交点P2(cos(-α),sin(-α))与点P(cos α,sin α)有怎样的关系?它们的三角函数之间有什么关系?
答案 角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称,它们的三角函数关系如下:
诱导公式二
sin-α=-sin α, cos-α=cos α, tan-α=-tan α.
知识点三 诱导公式三
思考 角π-α的终边与角α的终边有什么关系?角π-α的终边与单位圆的交点P3(cos(π-α),sin(π-α))与点P(cos α,sin α)有怎样的关系?它们的三角函数之间有什么关系?
答案 角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称,它们的三角函数关系如下:
诱导公式三
sin(π-α)=sin α, cos(π-α)=-cos α, tan(π-α)=-tan α.
梳理 公式一~三都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数之间的关系,这三组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.
知识点四 诱导公式四
完成下表,并由此总结角α,角-α的三角函数值间的关系.
(1)sin=,cos=,sin=cos;
(2)sin=,cos=,sin=cos;
(3)sin=,cos=,sin=cos.
由此可得
诱导公式四
sin=cos α, cos=sin α,
知识点五 诱导公式五
思考 能否利用已有公式得出+α的正弦、余弦与角α的正弦、余弦之间的关系?
答案 以-α代替公式四中的α得到
sin=cos(-α),
cos=sin(-α).
由此可得
诱导公式五
sin=cos α, cos=-sinα.
知识点六 诱导公式的推广与规律
1.sin=-cos α,cos=-sin α,
sin=-cos α,cos=sin α.
2.诱导公式记忆规律:
公式一~三归纳:α+2kπ(k∈Z),-α,π±α的三角函数值,等于角α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名不变,符号看象限”.
公式四~五归纳:±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名改变,符号看象限”或“正变余、余变正、符号象限定”.
五组诱导公式可以统一概括为“k·±α(k∈Z)”的诱导公式.
记忆口诀:奇变偶不变,符号看象限.其中“奇、偶”是指k·±α(k∈Z)中k的奇偶性,当k为奇数时,正弦变余弦,余弦变正弦;当k为偶数时,函数名不变.“符号”看的应该是诱导公式中,把α看成锐角时原函数值的符号,而不是α函数值的符号.
题型一 利用诱导公式求值
命题角度1 给角求值问题
例1-1 求下列各三角函数值:
(1)sin;(2)cos;(3)tan(-855°).
解析:(1)sin=sin=sinπ
=sin=-sin=-.
(2)cos=cos=cosπ=cos
=-cos=-.
(3)tan(-855°)=tan(-3×360°+225°)
=tan225°=tan(180°+45°)=tan45°=1.
变式训练1-1 求下列各三角函数式的值:
(1)sin 1 320°;(2)cos;(3)tan(-945°).
解析: (1) sin 1 320°=sin(3×360°+240°)
=sin 240°=sin(180°+60°)=-sin 60°=-.
(2) cos=cos
=cos=-cos=-.
(3)tan(-945°)=-tan 945°=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)=-tan 45°=-1.
命题角度2 给值求值或给值求角问题
例1-2 (1)已知sin(π+θ)=-cos(2π-θ),|θ|<,则θ等于( )
A.- B.- C. D.
答案 D
解析: 由sin(π+θ)=-cos(2π-θ),|θ|<,
可得-sin θ=-cos θ,|θ|<,
即tan θ=,|θ|<,∴θ=.
(2)已知cos=,求cos-sin2的值.
解析: 因为cos=cos
=-cos=-,
sin2=sin2=1-cos2
=1-2=,
所以cos-sin2=--=-.
变式训练1-2 已知sin β=,cos(α+β)=-1,则sin(α+2β)的值为( )
A.1 B.-1 C. D.-
解析: 由cos(α+β)=-1,得α+β=2kπ+π(k∈Z),
则α+2β=(α+β)+β=2kπ+π+β(k∈Z),
sin(α+2β)=sin(2kπ+π+β)=sin(π+β)
=-sin β=-.
答案 D
题型二 利用诱导公式化简
例2 已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且sin(α-π)=,
求f(α)的值;
(3)若α=-,求f(α)的值.
解析: (1)f(α)==-cos α.
(2)∵sin(α-π)=-sin α=,
∴sin α=-.又α是第三象限角,
∴cos α=-.∴f(α)=.
(3)∵-=-6×2π+,
∴f=-cos
=-cos
=-cos
=-.
变式训练2 化简:
·sin(α-2π)·cos(2π-α).
解析: 原式=·[-sin(2π-α)]·cos(2π-α)
=·sin α·cos α
=cos2α.
题型三 利用诱导公式求值
例3、 已知cos=,≤α≤,
求sin的值.
解析: ∵α+=+,
∴sin=sin=cos=.
变式训练3
已知sin=,求cos的值.
解析: ∵+α+-α=,
∴-α=-.
∴cos=cos
=sin=.
题型四 利用诱导公式证明三角恒等式
规律方法
例4、
求证:=-tan α.
证明: ∵左边=
=
=
==-
=-tan α=右边.
∴原等式成立.
变式训练4
求证:=.
证明: 右边=
=
=
=
===左边,
所以原等式成立.
题型五 诱导公式的综合应用
规律方法
例5 已知f(α)=.
(1)化简f(α);
(2)若角A是△ABC的内角,且f(A)=,
求tan A-sin A的值.
解析: (1)f(α)==cos α.
(2)因为f(A)=cos A=,
又A为△ABC的内角,
所以由平方关系,得sin A==,
所以tan A==,
所以tan A-sin A=-=.
变式训练5
已知f(α)=.
(1)化简f(α);
(2)若f=-,且α是第二象限角,求tan α.
解析:
(1)f(α)=
==sin α.
(2)由sin=-,得cos α=-,
又α是第二象限角,所以sin α==,
则tan α==-.
一、选择题
1.已知tan α=4,则tan(π-α)等于( )
A.π-4 B.4 C.-4 D.4-π
解析: tan(π-α)=-tan α=-4.
答案 C
2.cos(π+x)等于( )
A.cos x B.-cos x
C.sin x D.-sin x
解析: 由诱导公式得cos(π+x)=-cos x.
答案 B
3.已知sin(π+α)=,且α是第四象限角,则cos(α-2π)的值是( )
A.- B. C.- D.
解析: 因为sin(π+α)=,且sin(π+α)=-sin α,
所以sin α=-,
又因为α是第四象限角,
所以cos(α-2π)=cos α=
==.
答案 B
4.记cos(-80°)=k,那么tan 100°等于( )
A. B.-
C. D.-
解析: ∵cos(-80°)=k,∴cos 80°=k,
∴sin 80°=,则tan 80°=.
∴tan 100°=-tan 80°=-.
答案 B
5.若sin(π-α)=log8,且α∈,则cos(π+α)的值为( )
A. B.-
C.± D.以上都不对
解析: ∵sin(π-α)=sin α=2-2=-,
α∈,
∴cos(π+α)=-cos α=-
=- =-.
答案 B
6.若cos(2π-α)=,则sin等于( )
A.- B.-
C. D.±
解析: ∵cos(2π-α)=cos(-α)=cos α=,
∴sin=-cos α=-.
答案 A
7.已知tan θ=2,则等于( )
A.2 B.-2 C.0 D.
解析: =
===-2.
答案 B
8.已知sin=,那么cos α等于( )
A.- B.-
C. D.
解析: sin=cos α,故cos α=,故选C.
答案 C
9.已知sin 10°=k,则cos 620°的值为( )
A.k B.-k C.±k D.不确定
解析: cos 620°=cos(360°+260°)=cos 260°=cos(270°-10°)=-sin 10°=-k
答案 B.
10.若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos C B.sin(A+B)=-sin C
C.cos=sin B D.sin=cos
解析: ∵A+B+C=π,∴A+B=π-C,
∴cos(A+B)=-cos C,sin(A+B)=sin C,故A,B项不正确;
∵A+C=π-B,∴=,
∴cos=cos=sin,故C项不正确;
∵B+C=π-A,
∴sin=sin=cos,故D项正确.
答案 D
二、填空题
11.已知600°角的终边上有一点P(a,-3),则a的值为______.
解析: tan 600°=tan(360°+240°)=tan(180°+60°)
=tan 60°=-=,即a=-.
答案 -
12. 的值是________.
解析: 原式=
=
=
===-2.
答案 -2
13.已知a=tan,b=cos ,c=sin,则a,b,c的大小关系是________.
解析: ∵a=-tan=-tan =-,
b=cos=cos =,
c=-sin=-sin=-,
∴b>a>c.
答案 b>a>c
14.化简= .
解析: 原式=
==-1.
答案 -1
三、解答题
15.求下列三角函数值.
(1)tanπ+cos(-1 650°)+sinπ;
(2)7cos270°+3sin270°+tan765°.
解析:(1)原式=tan+cos1650°+sin
=-tan+cos(4×360°+210°)-sin
=-1+cos210°-
=-1+cos(180°+30°)-
=--cos30°
=--.
(2)原式=7cos(180°+90°)+3sin(180°+90°)+tan(2×360°+45°)
=-7cos90°-3sin90°+tan45°
=-2.
16.化简下列各式:
(1);
(2).
解析: (1)原式=
=
=1.
(2)原式=
=
==.
17.已知角α的终边经过单位圆上的点P.
(1)求sin α的值;
(2)求·的值.
解析: (1)∵点P在单位圆上,
∴由正弦的定义得sin α=-.
(2)原式=·==,
由余弦的定义得cos α=,
故原式=.
一、选择题
1.已知sin=,则sin的值为( )
A. B.- C. D.-
解析: sin=sin
=sin=.
答案 C
2.化简sin2(π+α)-cos(π+α)·cos(-α)+1的值为( )
A.1 B.2sin2α C.0 D.2
解析: 原式=(-sin α)2-(-cos α)·cos α+1=sin2α+cos2α+1=2.
答案 D
3.已知n为整数,化简所得的结果是( )
A.tan nα B.-tan nα
C.tan α D.-tan α
解析: 当n=2k,k∈Z时,=
==tan α;
当n=2k+1,k∈Z时,=
===tan α.故选C.
答案 C
4.已知sin=,则cos的值为( )
A. B.- C. D.-
解析: cos=cos
=sin=.
答案 C
5.化简sin·cos·tan的结果是( )
A.1 B.sin2α C.-cos2α D.-1
解析: 因为sin=cos α,
cos=cos=-sin α,
tan==,
所以原式=cos α(-sin α)=-cos2α,故选C.
答案 C
6.已知f(sin x)=cos 3x,则f(cos 10°)的值为( )
A.- B. C.- D.
解析: f(cos 10°)=f(sin 80°)=cos 240°
=cos(180°+60°)=-cos 60°=-.
答案 A
7.若sin(π+α)+cos=-m,则cos+2sin(2π-α)的值为( )
A.- B. C.- D.
解析: ∵sin(π+α)+cos=-sin α-sin α=-m,∴sin α=.
故cos+2sin(2π-α)=-sin α-2sin α
=-3sin α=-.
答案 C
8.下列式子中正确的是( )
A.sin(π-α)=-sinα
B.cos(π+α)=cosα
C.cosα=sinα
D.sin(2π+α)=sinα
解析:对于选项A,令α=,得sin(π-α)=sin=1≠-sin,所以A错误;
对于选项B,令α=0,得cos(π+α)=cosπ=-1≠cos0,所以B错误;
对于选项C,令α=0,得cosα=cos0=1≠sin0,所以C错误.
答案 D
9.已知函数f(x)=asin(πx+α)+bcos(πx+β)+4,x∈R,且f(2017)=3,则f(2018)的值为( )
A.3 B.4
C.5 D.6
解析:∵f(2017)=asin(2017π+α)+bcos(2017π+β)+4=3,
∴asin(2017π+α)+bcos(2017π+β)=-1,
∴f(2018)=asin(2017π+α+π)+bcos(2017π+β+π)+4
=-asin(2017π+α)-bcos(2017π+β)+4=1+4=5.
答案 C
10.计算sin21°+sin22°+sin23°+…+sin289°=( )
A.89 B.90
C. D.45
解析:
原式=sin21°+sin22°+sin23°+…+sin244°+sin245°+sin2(90°-44°)+…+sin2(90°-3°)
+sin2(90°-2°)+sin2(90°-1°)
=sin21°+sin22°+sin23°+…+sin244°+sin245°+cos244°+…+cos23°+cos22°+cos21°
=(sin21°+cos21°)+(sin22°+cos22°)+(sin23°+cos23°)+…+(sin244°+cos244°)+sin245°
=44+
=.
答案 C
二、填空题
11.化简=________.
解析: =
===1.
答案 1
12.设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β为非零常数,若f(2 017)=-1,则f(2 018)=________.
解析: ∵f(2 018)=asin(2 018π+α)+bcos(2 018π+β)
=asin(π+2 017π+α)+bcos(π+2 017π+β)
=-asin(2 017π+α)-bcos(2 017π+β)
=-f(2 017),
又f(2 017)=-1,∴f(2 018)=1.
答案 1
13.已知f(x)=则f+f的值为________.
解析: 因为f=sin
=sin=sin=;
f=f-1=f-2
=sin-2=--2=-,
所以f+f=-2.
答案 -2
14.给出下列三个结论,其中正确结论的序号是 .
①sin(π+α)=-sin α成立的条件是角α是锐角;
②若cos(nπ-α)=(n∈Z),则cos α=;
③若α≠(k∈Z),则tan=.
解析: 由诱导公式二,知α∈R时,sin(π+α)=-sin α,所以①错误.
当n=2k(k∈Z)时,cos(nπ-α)=cos(-α)=cos α,此时cos α=,
当n=2k+1(k∈Z)时,cos(nπ-α)=cos[(2k+1)π-α]=cos(π-α)=-cos α,此时cos α=-,所以②错误.
若α≠(k∈Z),则tan===-,所以③正确.
答案 ③
三、解答题
15. 化简下列各式:
(1);
(2).
解析: (1)原式=
==-=-tan α.
(2)原式=
==
==-1.
16.已知sin(5π-θ)+sin=,求sin4+cos4的值.
解析: ∵sin(5π-θ)+sin
=sin(π-θ)+sin
=sin θ+cos θ=,
∴sin θcos θ=[(sin θ+cos θ)2-1]
=×=,
∴sin4+cos4=cos4θ+sin4θ
=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-2×2=.
17.已知α是第四象限角,且f(α)=.
(1)若cos=,求f(α)的值;
(2)若α=-1 860°,求f(α)的值.
解析: f(α)=
==.
(1)∵cos=,
∴cos=,
∴cos=,
∴sin α=-,∴f(α)==-5.
(2)当α=-1 860°时,f(α)=
==
==
=-.
18.是否存在角α,β,α∈,β∈(0,π),使等式sin(3π-α)=cos,
cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
解析:假设存在角α,β满足条件,
则
①2+②2,得sin2α+3cos2α=2.
∴cos2α=,∴cosα=±.
∵α∈,∴cosα=.
由cosα=,cosα=cosβ,
得cosβ=.∵β∈(0,π),∴β=,
∴sinβ=,结合①可知sinα=,
则α=.
故存在α=,β=满足条件.
