2.2.2对数函数及其性质课件-2021-2022学年高一上学期数学人教A版必修1(共20张PPT)
文档属性
| 名称 | 2.2.2对数函数及其性质课件-2021-2022学年高一上学期数学人教A版必修1(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 203.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 18:55:28 | ||
图片预览

文档简介
(共20张PPT)
对数函数及其性质
杨京
四川省德阳中学校
2021 年 10 月 20 日
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
情境引入
阅读材料
类比指数函数的定义,给对数函数下一个定义
定义 (指数函数)
一般地,函数 y = ax(a > 0, 且a ≠ 1) 叫做指数函数 (exponential function),其中指 数 x 是自变量,定义域是 R.
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
对数函数的概念
定义 (对数函数)
一般地,函数 y = loga x(a > 0, 且a ≠ 1) 叫做对数函数 (logarithmic function),其中
真数 x 是自变量,定义域是 .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
判断对数函数
例题
判断下列函数是否为 y 关于 x 的对数函数,
y = loga x(a为常数)
y = log2 x 1
y = 2 log2 x
y = log2 x2
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
x y = log2 x
0.5
1
2
4
8
16
x
探究 y = log2 x 图像
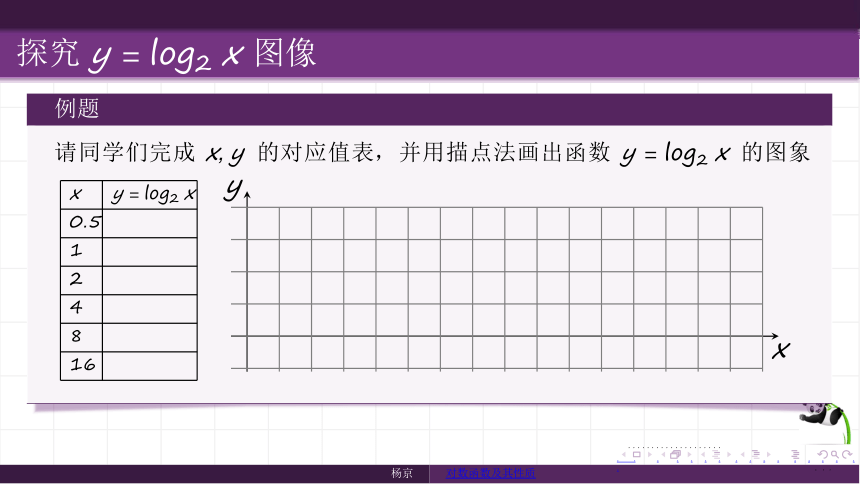
例题
请同学们完成 x, y 的对应值表,并用描点法画出函数 y = log2 x 的图象
y
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
x
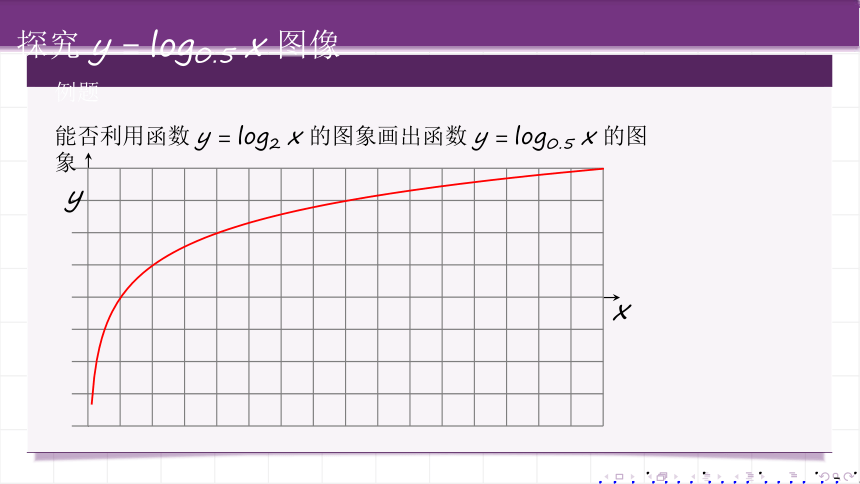
探究 y = log0.5 x 图像
例题
能否利用函数 y = log2 x 的图象画出函数 y = log0.5 x 的图象
y
. . . .. . . . .. . . . .. . . . .. . .. . . .
探究 y = loga x 图像
例题
选取底数 a(a > 0, 且a ≠ 1) 的若干个不同的值 (比如 a = 2,1/2, 3,1/3 ) ,在同一直
角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化 趋势,它们有哪些相同点和不同点?
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究一 (定点问题)
例题
函数 y = loga(x 1) + 2 一定过点
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. .
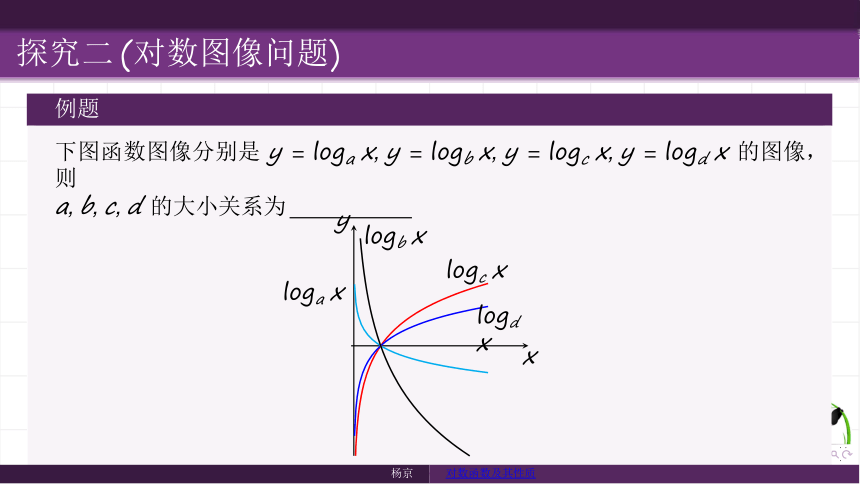
探究二 (对数图像问题)
例题
下图函数图像分别是 y = loga x, y = logb x, y = logc x, y = logd x 的图像,则
a, b, c, d 的大小关系为
x
y
loga x
.
杨京
对数函数及其性质
logb x
logc x
logd x
探究三 (定义域与值域)
例题
求下列函数的定义域:
x 2
(1)y = log (5 x);
(2)y =
杨京
对数函数及其性质
探究三 (对数不等式的解法
例题
解对数不等式
1
x 2
(1)log ≥ 1;
(2)log0.7(2x) < log0.7(x 1);
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究三 (定义域与值域)
例题
求下列函数的值域:
(1)y = log0.5(x2 + 2x + 3);
1
4
(2)y = log(4x) · log(2x), ≤ x ≤ 4;
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究四 (比大小)
例题
求下列两个数的大小 (1)log3.1 0.5, log3.1 0.2; (2)log0.1 0.6, log0.1 5; (3)log5 6, log6 5
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究五 (复合函数单调性 1)
例题
求函数 y = log0.5 x2 3x + 4 的单调性
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究五 (复合函数单调性 2)
例题
已知函数 y = loga(2 ax) 是区间 [0, 1] 上的减函数,则实数 a 的取值范围 为
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究六 (奇偶性)
例题
试判断函数 y = log2( ) 的奇偶性
例题
1 + x
试判断函数 y = log2 1 x 的奇偶性
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (与图像的结合 1)
例题
已知函数 f (x) = | log2 x|,x1 , x2 为方程 f (x) = m 的两个不相等的实数根,则
x1x2 = , 若 x1 < x2,则 x1 + x2 的范围为
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (与图像的结合 2)
例题
的两个不相等的实数根,试
已知函数 f (x) = | log2 x|,x1 , x2 为方程 f (x) =
比较 x1x2 与 1 的大小关系
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (反函数)
例题
已知函数 y = ex 1 与 y = x 相切, 试讨论方程 ax 1 = ln x + 1 根的个数.
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
总结
谈谈收获
通过这节课的学习,你对对 数函数的图像与性质有了 怎样的认识?
0 < a < 1
a > 1
图像
定义域
值域
单调性 定点 其它
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
对数函数及其性质
杨京
四川省德阳中学校
2021 年 10 月 20 日
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
情境引入
阅读材料
类比指数函数的定义,给对数函数下一个定义
定义 (指数函数)
一般地,函数 y = ax(a > 0, 且a ≠ 1) 叫做指数函数 (exponential function),其中指 数 x 是自变量,定义域是 R.
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
对数函数的概念
定义 (对数函数)
一般地,函数 y = loga x(a > 0, 且a ≠ 1) 叫做对数函数 (logarithmic function),其中
真数 x 是自变量,定义域是 .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
判断对数函数
例题
判断下列函数是否为 y 关于 x 的对数函数,
y = loga x(a为常数)
y = log2 x 1
y = 2 log2 x
y = log2 x2
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
x y = log2 x
0.5
1
2
4
8
16
x
探究 y = log2 x 图像
例题
请同学们完成 x, y 的对应值表,并用描点法画出函数 y = log2 x 的图象
y
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
x
探究 y = log0.5 x 图像
例题
能否利用函数 y = log2 x 的图象画出函数 y = log0.5 x 的图象
y
. . . .. . . . .. . . . .. . . . .. . .. . . .
探究 y = loga x 图像
例题
选取底数 a(a > 0, 且a ≠ 1) 的若干个不同的值 (比如 a = 2,1/2, 3,1/3 ) ,在同一直
角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化 趋势,它们有哪些相同点和不同点?
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究一 (定点问题)
例题
函数 y = loga(x 1) + 2 一定过点
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. .
探究二 (对数图像问题)
例题
下图函数图像分别是 y = loga x, y = logb x, y = logc x, y = logd x 的图像,则
a, b, c, d 的大小关系为
x
y
loga x
.
杨京
对数函数及其性质
logb x
logc x
logd x
探究三 (定义域与值域)
例题
求下列函数的定义域:
x 2
(1)y = log (5 x);
(2)y =
杨京
对数函数及其性质
探究三 (对数不等式的解法
例题
解对数不等式
1
x 2
(1)log ≥ 1;
(2)log0.7(2x) < log0.7(x 1);
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究三 (定义域与值域)
例题
求下列函数的值域:
(1)y = log0.5(x2 + 2x + 3);
1
4
(2)y = log(4x) · log(2x), ≤ x ≤ 4;
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究四 (比大小)
例题
求下列两个数的大小 (1)log3.1 0.5, log3.1 0.2; (2)log0.1 0.6, log0.1 5; (3)log5 6, log6 5
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究五 (复合函数单调性 1)
例题
求函数 y = log0.5 x2 3x + 4 的单调性
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究五 (复合函数单调性 2)
例题
已知函数 y = loga(2 ax) 是区间 [0, 1] 上的减函数,则实数 a 的取值范围 为
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究六 (奇偶性)
例题
试判断函数 y = log2( ) 的奇偶性
例题
1 + x
试判断函数 y = log2 1 x 的奇偶性
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (与图像的结合 1)
例题
已知函数 f (x) = | log2 x|,x1 , x2 为方程 f (x) = m 的两个不相等的实数根,则
x1x2 = , 若 x1 < x2,则 x1 + x2 的范围为
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (与图像的结合 2)
例题
的两个不相等的实数根,试
已知函数 f (x) = | log2 x|,x1 , x2 为方程 f (x) =
比较 x1x2 与 1 的大小关系
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
探究七 (反函数)
例题
已知函数 y = ex 1 与 y = x 相切, 试讨论方程 ax 1 = ln x + 1 根的个数.
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
总结
谈谈收获
通过这节课的学习,你对对 数函数的图像与性质有了 怎样的认识?
0 < a < 1
a > 1
图像
定义域
值域
单调性 定点 其它
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
杨京
对数函数及其性质
