2021-2022学年高一上学期数学人教B版(2019)必修第二册第六章平面向量初步章末复习导学案(Word 含答案)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第二册第六章平面向量初步章末复习导学案(Word 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 235.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览




文档简介
第六章 平面向量初步章末复习
学习目标
1.通过引导学生画出本章知识结构图,让学生从整体上把握本章的知识结构;
2.通过典型例题进一步提升学生数学运算、直观想象和逻辑推理的核心素养.
自主预习
自主复习平面向量一章,试着画出本章的知识结构图.
课堂探究
一、体系构建 结构完善
进一步完善本章知识结构图
二、题型分类 典例精讲
题型一 平面向量的线性运算
例1 如图,在△ABC中,点M是AB边的中点,E是中线CM的中点,AE的延长线交BC于F,MH∥AF交BC于H.求证:==.
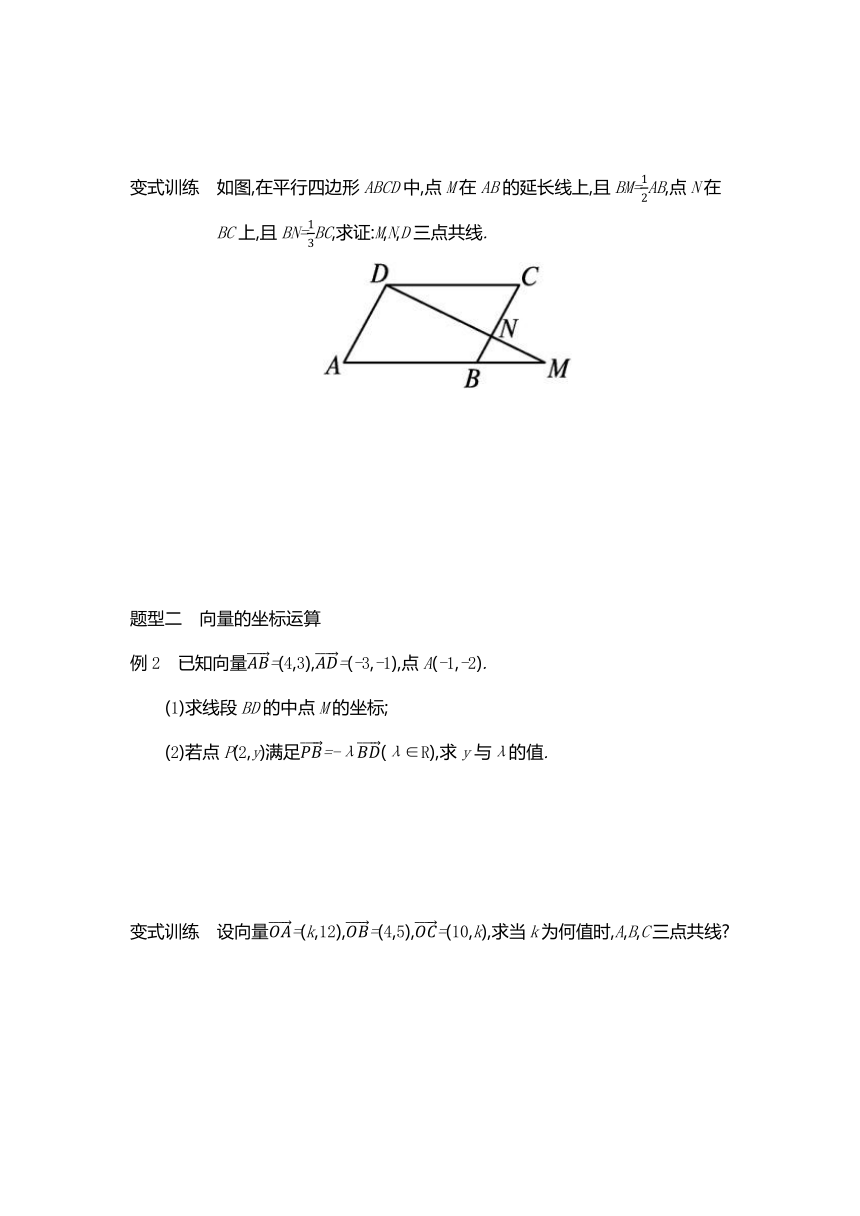
变式训练 如图,在平行四边形ABCD中,点M在AB的延长线上,且BM=AB,点N在BC上,且BN=BC,求证:M,N,D三点共线.
题型二 向量的坐标运算
例2 已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=-λ(λ∈R),求y与λ的值.
变式训练 设向量=(k,12),=(4,5),=(10,k),求当k为何值时,A,B,C三点共线
题型三 平面向量的应用
例3 已知正方形ABCD,E,F分别是CD,AD的中点,BE,CF交于点P.求证:AP=AB.
变式训练 在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,则小船的行进方向应指向哪里
核心素养专练
(一)基础过关
1.已知两点A(1,2),B(4,-2),则与向量共线的单位向量e=( )
A.(3,-4) B.(3,-4),(-3,4)
C. D.,
2.已知e1,e2是不共线向量,=2e1+e2,=-e1+3e2,=λe1-e2,且A,B,D三点共线,则实数λ等于 ( )
A.3 B.4 C.5 D.6
3.在正方形ABCD中,M,N分别是BC,CD的中点,若=λ+μ,则λ+μ=( )
A.2 B. C. D.
4.(多选)下列说法中正确的是( )
A.若|a|=|b|,则a∥b
B.若a∥b,b∥c,则a∥c
C.互为相反向量的两个向量模相等
D.++-=0
5.已知a=(2,1),b=(k,3),若(a+2b)∥(2a-b),则k= .
6. 如图,在平行四边形ABCD中,M为BC的中点,若=λ+μ,则λμ= .
7.如图,已知在△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设
=a,=b.
(1)用a,b表示向量,;
(2)若向量与+k共线,求k的值.
(二)能力提升
1.设D为△ABC所在平面内一点,=-+,若=λ(λ∈R),则λ=( )
A.2 B.3 C.-2 D.-3
2.O为△ABC内一点,且2++=0,=t,若B,O,D三点共线,则t的值为( )
A. B. C. D.
3.(多选)若点O是线段BC外一点,点P是平面上任意一点,且=λ+μ(λ,μ∈R),则下列说法正确的有( )
A.若λ+μ=1且λ>0,则点P在线段BC的延长线上
B.若λ+μ=1且λ<0,则点P在线段BC的延长线上
C.若λ+μ>1,则点P在△OBC外
D.若λ+μ<1,则点P在△OBC内
4.(多选)如图,已知△OAB,由射线OA和射线OB及线段AB构成如图所示的阴影区(不含边界).已知下列四个向量中对于点M1,M2,M3,M4,落在阴影区域内(不含边界)的有( )
A.=+2 B.=+
C.=+ D.=+
5.如图,在平行四边形ABCD中,E,F分别是CD和BC的中点,若=x+y(x,y∈R),则2x+y= ;若=λ+μ(λ,μ∈R),则3λ+3μ= .
参考答案
自主预习 略
课堂探究
一、
二、
例1 证明:设=a,=b,则=a+b,
=++=-+2+2=-a-b+2a+2b=a+b,
=+=+=-++=-b++-
=-b+a+2-=-b+a+2b-b=a+b.
综上,==.
变式训练:证明:设=a,=b,则==b,
∵==b,==a,
∴=-=b-a,
又=-=b-a=3=3,
∴向量与共线,
又M是向量与的公共点,故M,N,D三点共线.
例2 解:(1)设点B的坐标为(x1,y1).
∵=(4,3),A(-1,-2),∴(x1+1,y1+2)=(4,3),
∴∴
∴B(3,1).同理可得D(-4,-3).
设线段BD的中点M的坐标为(x2,y2),
则x2==-,y2==-1,
∴M.
(2)由已知得=(3,1)-(2,y)=(1,1-y),
=(-4,-3)-(3,1)=(-7,-4).
又=-λ,∴(1,1-y)=λ(-7,-4),
则∴
变式训练:
解:方法一:若A,B,C三点共线,则与共线,则存在实数λ,使得=λ,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k,-7)=λ(10-k,k-12),
即解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
方法二:由题意得,与共线,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k)(k-12)+7(10-k)=0,
即k2-9k-22=0,解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
例3 证明:如图建立直角坐标系,其中A为原点,不妨设AB=2,则A(0,0),B(2,0),C(2,2),E(1,2),F(0,1).
设P(x,y),则=(x,y-1),=(-2,-1),
∵∥,∴-x=-2(y-1),即x=2y-2,
同理由∥,得y=-2x+4,代入x=2y-2,
解得x=,∴y=,即P.
∴||==2.
∴AP=AB.
变式训练:解:如图所示,设向量的长度和方向表示水流速度的大小和方向,向量的长度和方向表示船在静水中速度的大小和方向,以,为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
核心素养专练
(一)基础过关
1.D 2.C 3.D 4.CD 5.6 6.
7.解:(1)∵A为BC的中点,
∴=(+),
可得=2-=2a-b,
而=-=-=2a-b.
(2)由(1),得+k=(2k+1)a-kb,
∵与+k共线,
设=λ(+k),
即2a-b=λ(2k+1)a+,
根据平面向量基本定理,得
解得k=.
(二)能力提升
1.D 2.B 3.BC 4.AB 5.2 4
学习目标
1.通过引导学生画出本章知识结构图,让学生从整体上把握本章的知识结构;
2.通过典型例题进一步提升学生数学运算、直观想象和逻辑推理的核心素养.
自主预习
自主复习平面向量一章,试着画出本章的知识结构图.
课堂探究
一、体系构建 结构完善
进一步完善本章知识结构图
二、题型分类 典例精讲
题型一 平面向量的线性运算
例1 如图,在△ABC中,点M是AB边的中点,E是中线CM的中点,AE的延长线交BC于F,MH∥AF交BC于H.求证:==.
变式训练 如图,在平行四边形ABCD中,点M在AB的延长线上,且BM=AB,点N在BC上,且BN=BC,求证:M,N,D三点共线.
题型二 向量的坐标运算
例2 已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=-λ(λ∈R),求y与λ的值.
变式训练 设向量=(k,12),=(4,5),=(10,k),求当k为何值时,A,B,C三点共线
题型三 平面向量的应用
例3 已知正方形ABCD,E,F分别是CD,AD的中点,BE,CF交于点P.求证:AP=AB.
变式训练 在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,则小船的行进方向应指向哪里
核心素养专练
(一)基础过关
1.已知两点A(1,2),B(4,-2),则与向量共线的单位向量e=( )
A.(3,-4) B.(3,-4),(-3,4)
C. D.,
2.已知e1,e2是不共线向量,=2e1+e2,=-e1+3e2,=λe1-e2,且A,B,D三点共线,则实数λ等于 ( )
A.3 B.4 C.5 D.6
3.在正方形ABCD中,M,N分别是BC,CD的中点,若=λ+μ,则λ+μ=( )
A.2 B. C. D.
4.(多选)下列说法中正确的是( )
A.若|a|=|b|,则a∥b
B.若a∥b,b∥c,则a∥c
C.互为相反向量的两个向量模相等
D.++-=0
5.已知a=(2,1),b=(k,3),若(a+2b)∥(2a-b),则k= .
6. 如图,在平行四边形ABCD中,M为BC的中点,若=λ+μ,则λμ= .
7.如图,已知在△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设
=a,=b.
(1)用a,b表示向量,;
(2)若向量与+k共线,求k的值.
(二)能力提升
1.设D为△ABC所在平面内一点,=-+,若=λ(λ∈R),则λ=( )
A.2 B.3 C.-2 D.-3
2.O为△ABC内一点,且2++=0,=t,若B,O,D三点共线,则t的值为( )
A. B. C. D.
3.(多选)若点O是线段BC外一点,点P是平面上任意一点,且=λ+μ(λ,μ∈R),则下列说法正确的有( )
A.若λ+μ=1且λ>0,则点P在线段BC的延长线上
B.若λ+μ=1且λ<0,则点P在线段BC的延长线上
C.若λ+μ>1,则点P在△OBC外
D.若λ+μ<1,则点P在△OBC内
4.(多选)如图,已知△OAB,由射线OA和射线OB及线段AB构成如图所示的阴影区(不含边界).已知下列四个向量中对于点M1,M2,M3,M4,落在阴影区域内(不含边界)的有( )
A.=+2 B.=+
C.=+ D.=+
5.如图,在平行四边形ABCD中,E,F分别是CD和BC的中点,若=x+y(x,y∈R),则2x+y= ;若=λ+μ(λ,μ∈R),则3λ+3μ= .
参考答案
自主预习 略
课堂探究
一、
二、
例1 证明:设=a,=b,则=a+b,
=++=-+2+2=-a-b+2a+2b=a+b,
=+=+=-++=-b++-
=-b+a+2-=-b+a+2b-b=a+b.
综上,==.
变式训练:证明:设=a,=b,则==b,
∵==b,==a,
∴=-=b-a,
又=-=b-a=3=3,
∴向量与共线,
又M是向量与的公共点,故M,N,D三点共线.
例2 解:(1)设点B的坐标为(x1,y1).
∵=(4,3),A(-1,-2),∴(x1+1,y1+2)=(4,3),
∴∴
∴B(3,1).同理可得D(-4,-3).
设线段BD的中点M的坐标为(x2,y2),
则x2==-,y2==-1,
∴M.
(2)由已知得=(3,1)-(2,y)=(1,1-y),
=(-4,-3)-(3,1)=(-7,-4).
又=-λ,∴(1,1-y)=λ(-7,-4),
则∴
变式训练:
解:方法一:若A,B,C三点共线,则与共线,则存在实数λ,使得=λ,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k,-7)=λ(10-k,k-12),
即解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
方法二:由题意得,与共线,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k)(k-12)+7(10-k)=0,
即k2-9k-22=0,解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
例3 证明:如图建立直角坐标系,其中A为原点,不妨设AB=2,则A(0,0),B(2,0),C(2,2),E(1,2),F(0,1).
设P(x,y),则=(x,y-1),=(-2,-1),
∵∥,∴-x=-2(y-1),即x=2y-2,
同理由∥,得y=-2x+4,代入x=2y-2,
解得x=,∴y=,即P.
∴||==2.
∴AP=AB.
变式训练:解:如图所示,设向量的长度和方向表示水流速度的大小和方向,向量的长度和方向表示船在静水中速度的大小和方向,以,为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
核心素养专练
(一)基础过关
1.D 2.C 3.D 4.CD 5.6 6.
7.解:(1)∵A为BC的中点,
∴=(+),
可得=2-=2a-b,
而=-=-=2a-b.
(2)由(1),得+k=(2k+1)a-kb,
∵与+k共线,
设=λ(+k),
即2a-b=λ(2k+1)a+,
根据平面向量基本定理,得
解得k=.
(二)能力提升
1.D 2.B 3.BC 4.AB 5.2 4
