2021-2022学年数学人教B版(2019)必修第二册6.2.3平面向量的坐标及其运算(第1课时) 导学案
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)必修第二册6.2.3平面向量的坐标及其运算(第1课时) 导学案 |  | |
| 格式 | docx | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 20:46:29 | ||
图片预览

文档简介
6.2.3平面向量的坐标及其运算
第1课时
学习目标
1.了解平面向量的正交分解,掌握向量的坐标表示.
2.掌握两个向量和、差及数乘向量的坐标运算法则和向量的模的公式.
3.正确理解向量坐标的概念,要把点的坐标与向量的坐标区分开来.
自主预习
1.直线的平行与向量的平行有什么联系与区别
2.怎样判断两条直线垂直
3.在边长为1的正三角形ABC中,|-|的值为 .
4.如图,在△ABC中,D是AB边上的点,且满足AD=3BD,设=a,=b,则向量用a,b表示为 .
课堂探究
1.向量的垂直
问题1 直线垂直是怎样定义的
如果平面上两个非零向量a,b所在的 ,我们就说平面向量 ,记作 ,为了方便起见,规定零向量与任意向量都垂直
即时训练 写出下列哪些向量是垂直的.
2.正交分解
问题2 前面我们学过平面向量基本定理,当基底为两个垂直向量时仍成立吗 思考并回答下面问题.
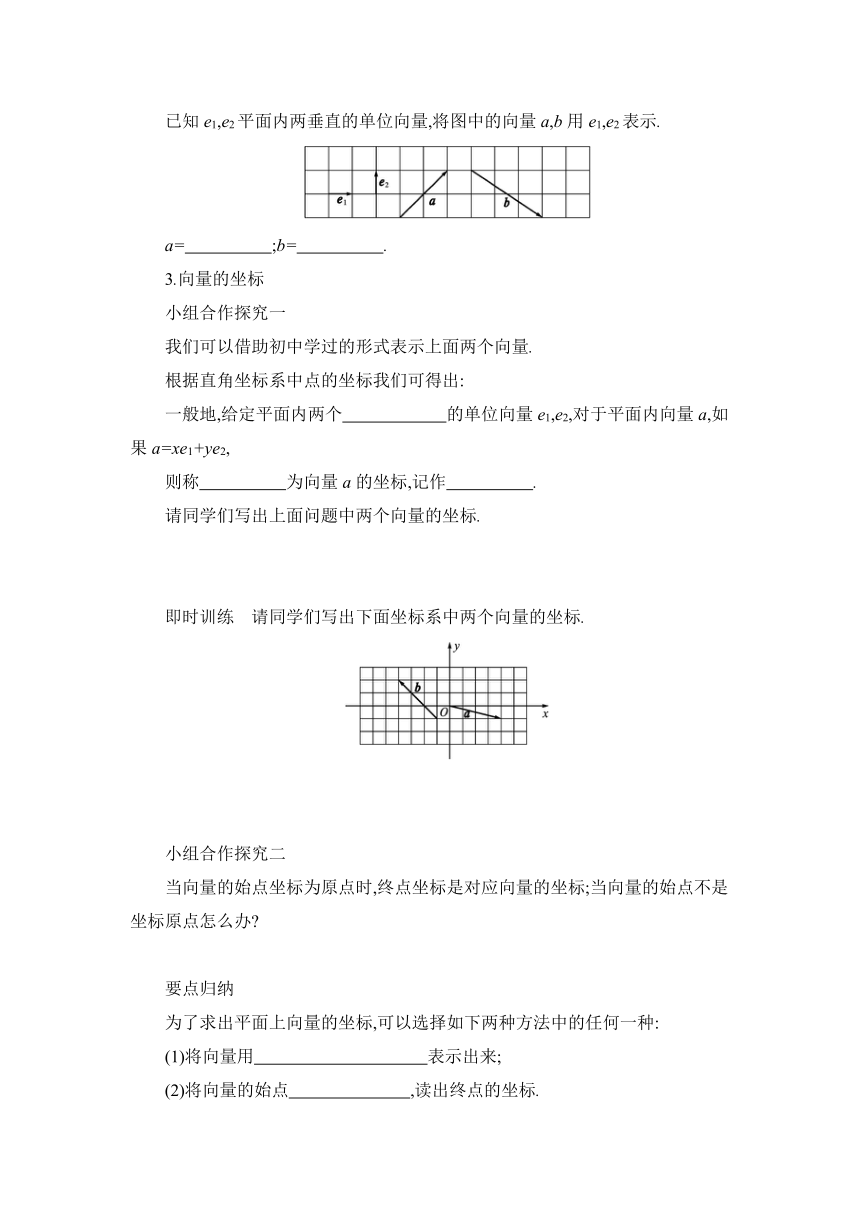
已知e1,e2平面内两垂直的单位向量,将图中的向量a,b用e1,e2表示.
a= ;b= .
3.向量的坐标
小组合作探究一
我们可以借助初中学过的形式表示上面两个向量.
根据直角坐标系中点的坐标我们可得出:
一般地,给定平面内两个 的单位向量e1,e2,对于平面内向量a,如果a=xe1+ye2,
则称 为向量a的坐标,记作 .
请同学们写出上面问题中两个向量的坐标.
即时训练 请同学们写出下面坐标系中两个向量的坐标.
小组合作探究二
当向量的始点坐标为原点时,终点坐标是对应向量的坐标;当向量的始点不是坐标原点怎么办
要点归纳
为了求出平面上向量的坐标,可以选择如下两种方法中的任何一种:
(1)将向量用 表示出来;
(2)将向量的始点 ,读出终点的坐标.
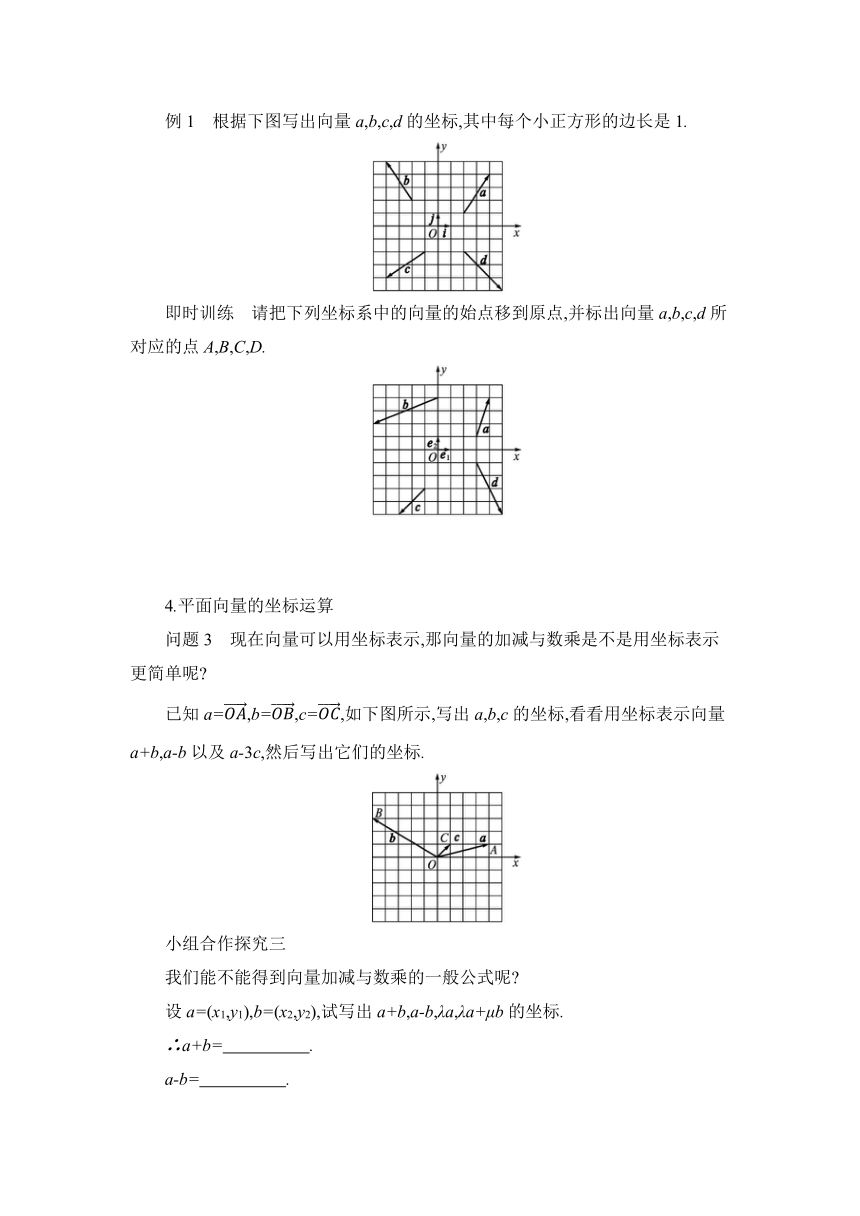
例1 根据下图写出向量a,b,c,d的坐标,其中每个小正方形的边长是1.
即时训练 请把下列坐标系中的向量的始点移到原点,并标出向量a,b,c,d所对应的点A,B,C,D.
4.平面向量的坐标运算
问题3 现在向量可以用坐标表示,那向量的加减与数乘是不是用坐标表示更简单呢
已知a=,b=,c=,如下图所示,写出a,b,c的坐标,看看用坐标表示向量a+b,a-b以及a-3c,然后写出它们的坐标.
小组合作探究三
我们能不能得到向量加减与数乘的一般公式呢
设a=(x1,y1),b=(x2,y2),试写出a+b,a-b,λa,λa+μb的坐标.
∴a+b= .
a-b= .
λa= .
λa+μb= .
例2 已知a=(-2,3),b=(3,1),c=(10,-4),试用a,b表示c.
要点归纳
待定系数法是最基本的数学方法之一,它的实质是先将未知量设出来,再利用方程或方程组求解,把一个向量用其他两个向量表示,这是常用方法.
课堂小结
通过本节课的学习,你有什么收获 (知识层面,思想方法层面)
核心素养专练
单项选择题
1.已知向量a=(1,2),b=(3,1),则b-a=( )
A.(-2,1) B.(2,-1) C.(2,0) D.(4,3)
多项选择题
2.已知,在平面上的点A(2,1),B(0,2),C(-2,1),O(0,0),下面结论正确的是( )
A.-=
B.+=
C.=-2
D.+2=
解答题
3.已知A(-2,4),B(3,-1),C(-3,-4).设=a,=b,=c.
(1)求3a+b;
(2)求满足a=mb+nc的实数m,n的值.
参考答案
自主预习 略
课堂探究
1.问题1 直线互相垂直 a与b垂直 a⊥b
即时训练 与,,,;与,,,等.
2.正交分解
问题2 成立
2e1+2e2 3e1-2e2
3.小组合作探究一
相互垂直 (x,y) a=(x,y) (2,2),(3,-2)
即时训练 (4,-1),(-3,3)
小组合作探究二
要点归纳 (1)单位向量 (2)平移到原点
例1 a=(2,3),b=(-2,3),c=(-3,-2),d=(3,-3).
即时训练 a==(1,3);b==(-5,-2);c==(-2,-2);d==(2,-4).
4.问题3 a+b=(-1,4),a-b=(9,-2),a-3c=(1,-2).
小组合作探究三
a+b=(x1+x2,y1+y2) a-b=(x1-x2,y1-y2)
λa=(λx1,λy1)
λa+μb=(λx1+μx2,λy1+μy2).
例2 解:设c=xa+yb,则(10,-4)=x(-2,3)+y(3,1)=(-2x+3y,3x+y),
∴解得∴c=-2a+2b.
核心素养专练
1.B 2.BC
3.解:a=(5,-5),b=(-6,-3),c=(1,8).
(1)3a+b=3(5,-5)+(-6,-3)=(15-6,-15-3)=(9,-18).
(2)∵mb+nc=(-6m+n,-3m+8n),
∴-6m+n=5,-3m+8n=-5,
解得m=n=-1.
第1课时
学习目标
1.了解平面向量的正交分解,掌握向量的坐标表示.
2.掌握两个向量和、差及数乘向量的坐标运算法则和向量的模的公式.
3.正确理解向量坐标的概念,要把点的坐标与向量的坐标区分开来.
自主预习
1.直线的平行与向量的平行有什么联系与区别
2.怎样判断两条直线垂直
3.在边长为1的正三角形ABC中,|-|的值为 .
4.如图,在△ABC中,D是AB边上的点,且满足AD=3BD,设=a,=b,则向量用a,b表示为 .
课堂探究
1.向量的垂直
问题1 直线垂直是怎样定义的
如果平面上两个非零向量a,b所在的 ,我们就说平面向量 ,记作 ,为了方便起见,规定零向量与任意向量都垂直
即时训练 写出下列哪些向量是垂直的.
2.正交分解
问题2 前面我们学过平面向量基本定理,当基底为两个垂直向量时仍成立吗 思考并回答下面问题.
已知e1,e2平面内两垂直的单位向量,将图中的向量a,b用e1,e2表示.
a= ;b= .
3.向量的坐标
小组合作探究一
我们可以借助初中学过的形式表示上面两个向量.
根据直角坐标系中点的坐标我们可得出:
一般地,给定平面内两个 的单位向量e1,e2,对于平面内向量a,如果a=xe1+ye2,
则称 为向量a的坐标,记作 .
请同学们写出上面问题中两个向量的坐标.
即时训练 请同学们写出下面坐标系中两个向量的坐标.
小组合作探究二
当向量的始点坐标为原点时,终点坐标是对应向量的坐标;当向量的始点不是坐标原点怎么办
要点归纳
为了求出平面上向量的坐标,可以选择如下两种方法中的任何一种:
(1)将向量用 表示出来;
(2)将向量的始点 ,读出终点的坐标.
例1 根据下图写出向量a,b,c,d的坐标,其中每个小正方形的边长是1.
即时训练 请把下列坐标系中的向量的始点移到原点,并标出向量a,b,c,d所对应的点A,B,C,D.
4.平面向量的坐标运算
问题3 现在向量可以用坐标表示,那向量的加减与数乘是不是用坐标表示更简单呢
已知a=,b=,c=,如下图所示,写出a,b,c的坐标,看看用坐标表示向量a+b,a-b以及a-3c,然后写出它们的坐标.
小组合作探究三
我们能不能得到向量加减与数乘的一般公式呢
设a=(x1,y1),b=(x2,y2),试写出a+b,a-b,λa,λa+μb的坐标.
∴a+b= .
a-b= .
λa= .
λa+μb= .
例2 已知a=(-2,3),b=(3,1),c=(10,-4),试用a,b表示c.
要点归纳
待定系数法是最基本的数学方法之一,它的实质是先将未知量设出来,再利用方程或方程组求解,把一个向量用其他两个向量表示,这是常用方法.
课堂小结
通过本节课的学习,你有什么收获 (知识层面,思想方法层面)
核心素养专练
单项选择题
1.已知向量a=(1,2),b=(3,1),则b-a=( )
A.(-2,1) B.(2,-1) C.(2,0) D.(4,3)
多项选择题
2.已知,在平面上的点A(2,1),B(0,2),C(-2,1),O(0,0),下面结论正确的是( )
A.-=
B.+=
C.=-2
D.+2=
解答题
3.已知A(-2,4),B(3,-1),C(-3,-4).设=a,=b,=c.
(1)求3a+b;
(2)求满足a=mb+nc的实数m,n的值.
参考答案
自主预习 略
课堂探究
1.问题1 直线互相垂直 a与b垂直 a⊥b
即时训练 与,,,;与,,,等.
2.正交分解
问题2 成立
2e1+2e2 3e1-2e2
3.小组合作探究一
相互垂直 (x,y) a=(x,y) (2,2),(3,-2)
即时训练 (4,-1),(-3,3)
小组合作探究二
要点归纳 (1)单位向量 (2)平移到原点
例1 a=(2,3),b=(-2,3),c=(-3,-2),d=(3,-3).
即时训练 a==(1,3);b==(-5,-2);c==(-2,-2);d==(2,-4).
4.问题3 a+b=(-1,4),a-b=(9,-2),a-3c=(1,-2).
小组合作探究三
a+b=(x1+x2,y1+y2) a-b=(x1-x2,y1-y2)
λa=(λx1,λy1)
λa+μb=(λx1+μx2,λy1+μy2).
例2 解:设c=xa+yb,则(10,-4)=x(-2,3)+y(3,1)=(-2x+3y,3x+y),
∴解得∴c=-2a+2b.
核心素养专练
1.B 2.BC
3.解:a=(5,-5),b=(-6,-3),c=(1,8).
(1)3a+b=3(5,-5)+(-6,-3)=(15-6,-15-3)=(9,-18).
(2)∵mb+nc=(-6m+n,-3m+8n),
∴-6m+n=5,-3m+8n=-5,
解得m=n=-1.
