2021-2022学年数学人教B版(2019)必修第二册6.3平面向量线性运算的应用(第1课时)导学案
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)必修第二册6.3平面向量线性运算的应用(第1课时)导学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览


文档简介
6.3平面向量线性运算的应用(第1课时)
学习目标
1.会用向量方法解决某些简单的平面几何问题,体现了逻辑推理和直观想象的核心素养.
2.会用向量方法解决某些简单的力学问题,及其他一些实际问题,体现了数学建模的核心素养.
自主预习
一、预习教材P168~170的内容,思考以下问题:
1.平面向量是如何体现在几何问题中的
2.平面向量是如何体现在物理问题中的
二、复习回顾:
1.若a=(x,y),则|a|=
2.若A(x1,y1),B(x2,y2),则||=
3.如何用向量法证明AB∥CD
4.如何用向量法证明A,B,C三点共线
5.若质点O在三个力F1,F2,F3的作用下处于平衡状态,则三个力满足的关系式为 .
三、自我检测:
1.在四边形ABCD中,=,且||=||,那么四边形ABCD为( )
A.平行四边形 B.菱形
C.长方形 D.正方形
2.已知三个力F1=(-2,-1),F2=(-3,2),F3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力F4,则F4等于( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
课堂探究
合作探究一:向量在平面几何中的应用
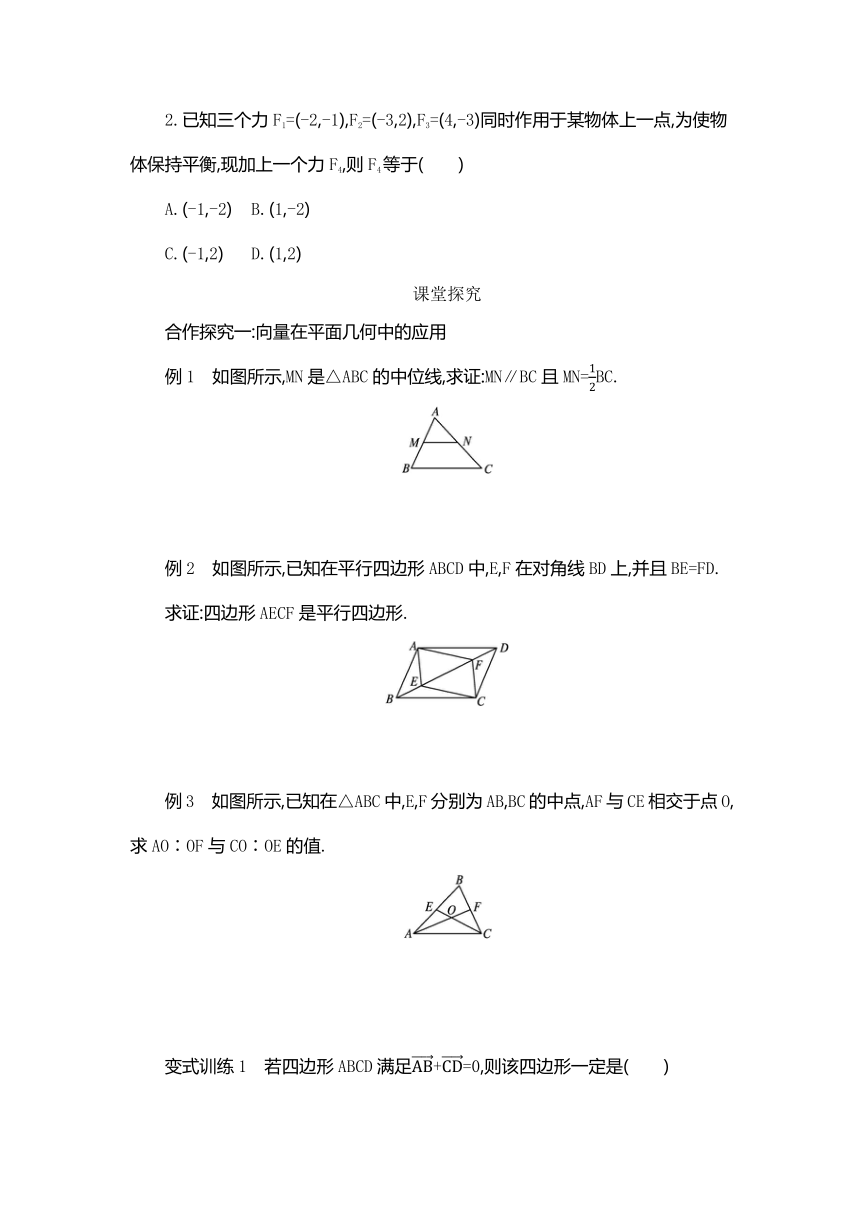
例1 如图所示,MN是△ABC的中位线,求证:MN∥BC且MN=BC.
例2 如图所示,已知在平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.
求证:四边形AECF是平行四边形.
例3 如图所示,已知在△ABC中,E,F分别为AB,BC的中点,AF与CE相交于点O,求AO∶OF与CO∶OE的值.
变式训练1 若四边形ABCD满足+=0,则该四边形一定是( )
A.正方形 B.矩形
C.菱形 D.平行四边形
合作探究二:向量在物理中的应用
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知物体所受的重力大小为50 N,求每条绳上的拉力大小.
变式训练2 用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10 N,则每根绳子的拉力大小为 N.
核心素养专练
1.已知四边形ABCD各顶点坐标是A,B,C,D,则四边形ABCD是 ( )
A.梯形 B.平行四边形
C.矩形 D.菱形
2.河水的流速为5 m/s,一艘小船想以12 m/s的速度沿垂直河岸方向驶向对岸,则小船的静水速度大小为( )
A.13 m/s B.12 m/s
C.17 m/s D.15 m/s
3.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
4.当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若|F|=|G|,则θ的值为( )
A.30° B.60° C.90° D.120°
5.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC= .
6.已知Rt△ABC中,∠C=90°,设AC=m,BC=n.
(1)若D为斜边AB的中点,求证:CD=AB;
(2)若E为CD的中点,连接AE并延长交BC于F,求AF的长度(用m,n表示).
参考答案
自主预习
略
课堂探究
例1 证明:因为M,N分别是AB,AC的中点,
所以=,=,因此
=-=-=(-)=,
所以MN∥BC且MN=BC.
例2 证明:设==a,==b,
则=+=a+b,=+=b+a,
所以=,因此AE FC
所以四边形AECF是平行四边形.
例3 设=s,=t,选取基底{,},
+=+=2+2=2=2-2,
+=s-t,
∴s-t=2-2,又∵,不共线,
∴∴s=t=2,∴AO∶OF=CO∶OE=2∶1.
变式训练1 D
例4 解:因为物体处于平衡状态,所以
F1+F2+G=0;∴|F1+F2|=|G|=50.
又由图及向量加法的平行四边形法则知:F1+F2的方向竖直向上的,
且|F1+F2|=2|F1|sin 45°=2|F2|sin 45°.
∴|F1|=|F2|==25 N,∴每条绳上的拉力为25 N.
变式训练2
解析:如图,由题意,得∠AOC=∠COB=60°,||=10,
则||=||=10,即每根绳子的拉力大小为10 N.
核心素养专练
1.A 2.A 3.B 4.D 5.1∶5
6.解:(1)证明:以C为坐标原点,以边CB,CA所在的直线分别为x轴,y轴建立平面直角坐标系,
如图所示,A(0,m),B(n,0).
∵D为AB的中点,∴D,
∴||=,
||=,
∴||=||,即CD=AB.
(2)∵E为CD的中点,∴E,
设F(x,0),则=,=(x,-m).
∵A,E,F三点共线,∴=λ.
即(x,-m)=λ,则
故λ=,即x=,∴F,
∴||=,即AF=.
学习目标
1.会用向量方法解决某些简单的平面几何问题,体现了逻辑推理和直观想象的核心素养.
2.会用向量方法解决某些简单的力学问题,及其他一些实际问题,体现了数学建模的核心素养.
自主预习
一、预习教材P168~170的内容,思考以下问题:
1.平面向量是如何体现在几何问题中的
2.平面向量是如何体现在物理问题中的
二、复习回顾:
1.若a=(x,y),则|a|=
2.若A(x1,y1),B(x2,y2),则||=
3.如何用向量法证明AB∥CD
4.如何用向量法证明A,B,C三点共线
5.若质点O在三个力F1,F2,F3的作用下处于平衡状态,则三个力满足的关系式为 .
三、自我检测:
1.在四边形ABCD中,=,且||=||,那么四边形ABCD为( )
A.平行四边形 B.菱形
C.长方形 D.正方形
2.已知三个力F1=(-2,-1),F2=(-3,2),F3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力F4,则F4等于( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
课堂探究
合作探究一:向量在平面几何中的应用
例1 如图所示,MN是△ABC的中位线,求证:MN∥BC且MN=BC.
例2 如图所示,已知在平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.
求证:四边形AECF是平行四边形.
例3 如图所示,已知在△ABC中,E,F分别为AB,BC的中点,AF与CE相交于点O,求AO∶OF与CO∶OE的值.
变式训练1 若四边形ABCD满足+=0,则该四边形一定是( )
A.正方形 B.矩形
C.菱形 D.平行四边形
合作探究二:向量在物理中的应用
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知物体所受的重力大小为50 N,求每条绳上的拉力大小.
变式训练2 用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10 N,则每根绳子的拉力大小为 N.
核心素养专练
1.已知四边形ABCD各顶点坐标是A,B,C,D,则四边形ABCD是 ( )
A.梯形 B.平行四边形
C.矩形 D.菱形
2.河水的流速为5 m/s,一艘小船想以12 m/s的速度沿垂直河岸方向驶向对岸,则小船的静水速度大小为( )
A.13 m/s B.12 m/s
C.17 m/s D.15 m/s
3.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
4.当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若|F|=|G|,则θ的值为( )
A.30° B.60° C.90° D.120°
5.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC= .
6.已知Rt△ABC中,∠C=90°,设AC=m,BC=n.
(1)若D为斜边AB的中点,求证:CD=AB;
(2)若E为CD的中点,连接AE并延长交BC于F,求AF的长度(用m,n表示).
参考答案
自主预习
略
课堂探究
例1 证明:因为M,N分别是AB,AC的中点,
所以=,=,因此
=-=-=(-)=,
所以MN∥BC且MN=BC.
例2 证明:设==a,==b,
则=+=a+b,=+=b+a,
所以=,因此AE FC
所以四边形AECF是平行四边形.
例3 设=s,=t,选取基底{,},
+=+=2+2=2=2-2,
+=s-t,
∴s-t=2-2,又∵,不共线,
∴∴s=t=2,∴AO∶OF=CO∶OE=2∶1.
变式训练1 D
例4 解:因为物体处于平衡状态,所以
F1+F2+G=0;∴|F1+F2|=|G|=50.
又由图及向量加法的平行四边形法则知:F1+F2的方向竖直向上的,
且|F1+F2|=2|F1|sin 45°=2|F2|sin 45°.
∴|F1|=|F2|==25 N,∴每条绳上的拉力为25 N.
变式训练2
解析:如图,由题意,得∠AOC=∠COB=60°,||=10,
则||=||=10,即每根绳子的拉力大小为10 N.
核心素养专练
1.A 2.A 3.B 4.D 5.1∶5
6.解:(1)证明:以C为坐标原点,以边CB,CA所在的直线分别为x轴,y轴建立平面直角坐标系,
如图所示,A(0,m),B(n,0).
∵D为AB的中点,∴D,
∴||=,
||=,
∴||=||,即CD=AB.
(2)∵E为CD的中点,∴E,
设F(x,0),则=,=(x,-m).
∵A,E,F三点共线,∴=λ.
即(x,-m)=λ,则
故λ=,即x=,∴F,
∴||=,即AF=.
