2021-2022学年数学人教B版(2019)必修第二册6.3平面向量线性运算的应用导学案
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)必修第二册6.3平面向量线性运算的应用导学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 113.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览


文档简介
6.3平面向量线性运算的应用
学习目标
考点 学习目标 核心素养
几何应用 通过本节课学习理解向量在处理有关平面几何问题中的优越性并体会向量在几何和现实生活中的意义 数学抽象、数学建模
物理应用 运用向量的有关知识(向量加减法与向量数量积的运算法则等)解决简单的物理问题 数学抽象、数学建模
自主预习
预习教材P168~170的内容,解决以下问题:
1.已知向量a=(-2,m)与向量b=(1-m,1)平行,则实数m的值为( )
A.-1 B.1 C.2 D.-1或2
2.已知三个力F1=(-2,-1),F2=(-3,2),F3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力F4,则F4等于( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
3.如图,已知点A(4,0),B(4,4),C(2,6),则AC与OB的交点P的坐标为 .
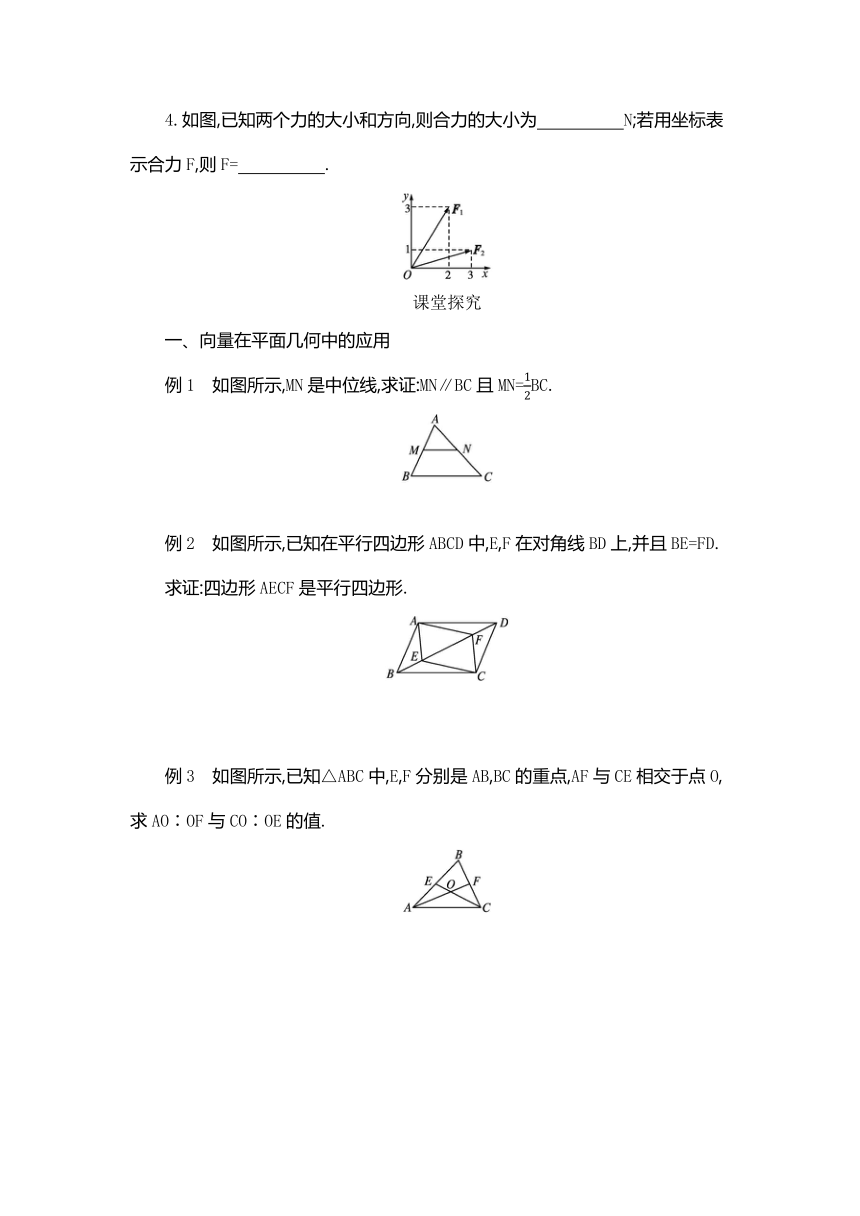
4.如图,已知两个力的大小和方向,则合力的大小为 N;若用坐标表示合力F,则F= .
课堂探究
一、向量在平面几何中的应用
例1 如图所示,MN是中位线,求证:MN∥BC且MN=BC.
例2 如图所示,已知在平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.
求证:四边形AECF是平行四边形.
例3 如图所示,已知△ABC中,E,F分别是AB,BC的重点,AF与CE相交于点O,求AO∶OF与CO∶OE的值.
跟踪训练 如图,在直角梯形ABCD中,=,=2,且=r+s,则2r+3s=( )
A.1 B.2 C.3 D.4
二、向量在物理中的应用
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已经物体所受的重力大小为50 N,求每条绳上的拉力大小.
跟踪训练 已知船在静水中的速度大小为5 m/s,且船在静水中的速度大小大于水的速度大小,河宽为20 m,船垂直到达对岸用的时间为5 s,试用向量的减法来求水流的速度大小.
课堂练习
1.已知点A(2,3),B(-2,6),C(6,6),D(10,3),则以ABCD为顶点的四边形是( )
A.梯形
B.邻边不相等的平行四边形
C.菱形
D.两组对边均不平行的四边形
2.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1),且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1) B.(1,9)
C.(9,0) D.(0,9)
3.已知在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=FC=AC,试用向量方法证明四边形DEBF也是平行四边形.
核心素养专练
1.人骑自行车的速度是v1,风速为v2,则人的实际速度为( )
A.v1-v2 B.v1+v2
C.|v1|-|v2| D.
2.已知四边形ABCD各顶点坐标是A,B,C,D,则四边形ABCD是 ( )
A.梯形 B.平行四边形
C.矩形 D.菱形
3.查阅资料,了解更多向量线性运算在平面几何和物理等方面的应用.
参考答案
自主预习
略
课堂探究
例1 证明:因为M,N分别是AB,AC边上的中点,所以=,=,因此
=-=-=(-)=,
从而可知MN∥BC且MN=BC.
例2 证明:由已知可设
==a,==b,
则=+=a+b,=+=b+a.
又因为a+b=b+a,所以=,
因此AE FC,从而可知四边形AECF是平行四边形.
例3 解:因为=+=+,
又因为E,F都是中点,所以
+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,
=t,则有s-t=2+2,
即(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,因此AO∶OF=CO∶OE=2∶1.
跟踪训练 C 解析:根据图形由题意可得
=+=+
=+(++)
=+(+)
=+
=+.因为=r+s,
所以r=,s=,
所以2r+3s=1+2=3.
例4 解:因为物体处于平衡状态,所以F1+F2是重力的相反向量,因此|F1+F2|=50 N.
又由图与向量加法的平行四边形法则可知,F1+F2的方向是竖直向上的,且|F1+F2|=2|F1|sin 45°=2|F2|sin 45°,
所以|F1|=|F2|==25 N.
因此,每条绳上的拉力为25 N.
跟踪训练 解:设船在静水中的速度为v1,水流速度为v2,船的实际速度为v3,建立如图坐标系.
|v1|=5,|v3|==4,则
v3=(0,4),v1=(-3,4),v2=v3-v1=(0,4)-(-3,4)=(3,0).
所以|v2|=3.即水流的速度大小为3 m/s.
课堂学习
1.B 解析:因为=(8,0),=(8,0),所以=,因为=(4,-3),所以||=5,而||=8,故为邻边不相等的平行四边形.
2.A 解析:F=F1+F2+F3=(3,4)+(2,-5)+(3,1)=(8,0),
设终点为B(x,y),则(x-1,y-1)=(8,0),
所以所以所以终点坐标为(9,1).
3.证明:设=a,=b,则=-=-a=b-a,
=-=b-=b-a,
所以=,且D,E,F,B四点不共线,所以四边形DEBF是平行四边形.
核心素养专练
1.B 解析:由向量的加法法则可得人的实际速度为v1+v2.注意速度是有方向和大小的,是一个向量.
2.A 解析:因为=,=(3,4),
所以=,所以∥,即AB∥DC.
又||==,||==5,
所以||≠||,所以四边形ABCD是梯形.
3.略
学习目标
考点 学习目标 核心素养
几何应用 通过本节课学习理解向量在处理有关平面几何问题中的优越性并体会向量在几何和现实生活中的意义 数学抽象、数学建模
物理应用 运用向量的有关知识(向量加减法与向量数量积的运算法则等)解决简单的物理问题 数学抽象、数学建模
自主预习
预习教材P168~170的内容,解决以下问题:
1.已知向量a=(-2,m)与向量b=(1-m,1)平行,则实数m的值为( )
A.-1 B.1 C.2 D.-1或2
2.已知三个力F1=(-2,-1),F2=(-3,2),F3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力F4,则F4等于( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
3.如图,已知点A(4,0),B(4,4),C(2,6),则AC与OB的交点P的坐标为 .
4.如图,已知两个力的大小和方向,则合力的大小为 N;若用坐标表示合力F,则F= .
课堂探究
一、向量在平面几何中的应用
例1 如图所示,MN是中位线,求证:MN∥BC且MN=BC.
例2 如图所示,已知在平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.
求证:四边形AECF是平行四边形.
例3 如图所示,已知△ABC中,E,F分别是AB,BC的重点,AF与CE相交于点O,求AO∶OF与CO∶OE的值.
跟踪训练 如图,在直角梯形ABCD中,=,=2,且=r+s,则2r+3s=( )
A.1 B.2 C.3 D.4
二、向量在物理中的应用
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已经物体所受的重力大小为50 N,求每条绳上的拉力大小.
跟踪训练 已知船在静水中的速度大小为5 m/s,且船在静水中的速度大小大于水的速度大小,河宽为20 m,船垂直到达对岸用的时间为5 s,试用向量的减法来求水流的速度大小.
课堂练习
1.已知点A(2,3),B(-2,6),C(6,6),D(10,3),则以ABCD为顶点的四边形是( )
A.梯形
B.邻边不相等的平行四边形
C.菱形
D.两组对边均不平行的四边形
2.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1),且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1) B.(1,9)
C.(9,0) D.(0,9)
3.已知在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=FC=AC,试用向量方法证明四边形DEBF也是平行四边形.
核心素养专练
1.人骑自行车的速度是v1,风速为v2,则人的实际速度为( )
A.v1-v2 B.v1+v2
C.|v1|-|v2| D.
2.已知四边形ABCD各顶点坐标是A,B,C,D,则四边形ABCD是 ( )
A.梯形 B.平行四边形
C.矩形 D.菱形
3.查阅资料,了解更多向量线性运算在平面几何和物理等方面的应用.
参考答案
自主预习
略
课堂探究
例1 证明:因为M,N分别是AB,AC边上的中点,所以=,=,因此
=-=-=(-)=,
从而可知MN∥BC且MN=BC.
例2 证明:由已知可设
==a,==b,
则=+=a+b,=+=b+a.
又因为a+b=b+a,所以=,
因此AE FC,从而可知四边形AECF是平行四边形.
例3 解:因为=+=+,
又因为E,F都是中点,所以
+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,
=t,则有s-t=2+2,
即(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,因此AO∶OF=CO∶OE=2∶1.
跟踪训练 C 解析:根据图形由题意可得
=+=+
=+(++)
=+(+)
=+
=+.因为=r+s,
所以r=,s=,
所以2r+3s=1+2=3.
例4 解:因为物体处于平衡状态,所以F1+F2是重力的相反向量,因此|F1+F2|=50 N.
又由图与向量加法的平行四边形法则可知,F1+F2的方向是竖直向上的,且|F1+F2|=2|F1|sin 45°=2|F2|sin 45°,
所以|F1|=|F2|==25 N.
因此,每条绳上的拉力为25 N.
跟踪训练 解:设船在静水中的速度为v1,水流速度为v2,船的实际速度为v3,建立如图坐标系.
|v1|=5,|v3|==4,则
v3=(0,4),v1=(-3,4),v2=v3-v1=(0,4)-(-3,4)=(3,0).
所以|v2|=3.即水流的速度大小为3 m/s.
课堂学习
1.B 解析:因为=(8,0),=(8,0),所以=,因为=(4,-3),所以||=5,而||=8,故为邻边不相等的平行四边形.
2.A 解析:F=F1+F2+F3=(3,4)+(2,-5)+(3,1)=(8,0),
设终点为B(x,y),则(x-1,y-1)=(8,0),
所以所以所以终点坐标为(9,1).
3.证明:设=a,=b,则=-=-a=b-a,
=-=b-=b-a,
所以=,且D,E,F,B四点不共线,所以四边形DEBF是平行四边形.
核心素养专练
1.B 解析:由向量的加法法则可得人的实际速度为v1+v2.注意速度是有方向和大小的,是一个向量.
2.A 解析:因为=,=(3,4),
所以=,所以∥,即AB∥DC.
又||==,||==5,
所以||≠||,所以四边形ABCD是梯形.
3.略
