2021-2022学年数学人教B版(2019)必修第二册第六章平面向量初步章末复习导学案
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)必修第二册第六章平面向量初步章末复习导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览


文档简介
第六章 平面向量初步章末复习
学习目标
能够从多种角度理解向量概念和运算法则,掌握向量基本定理;能够运用向量运算解决简单的几何和物理问题,知道数学运算与逻辑推理的关系.
自主预习
基础知识回顾
讲授新课
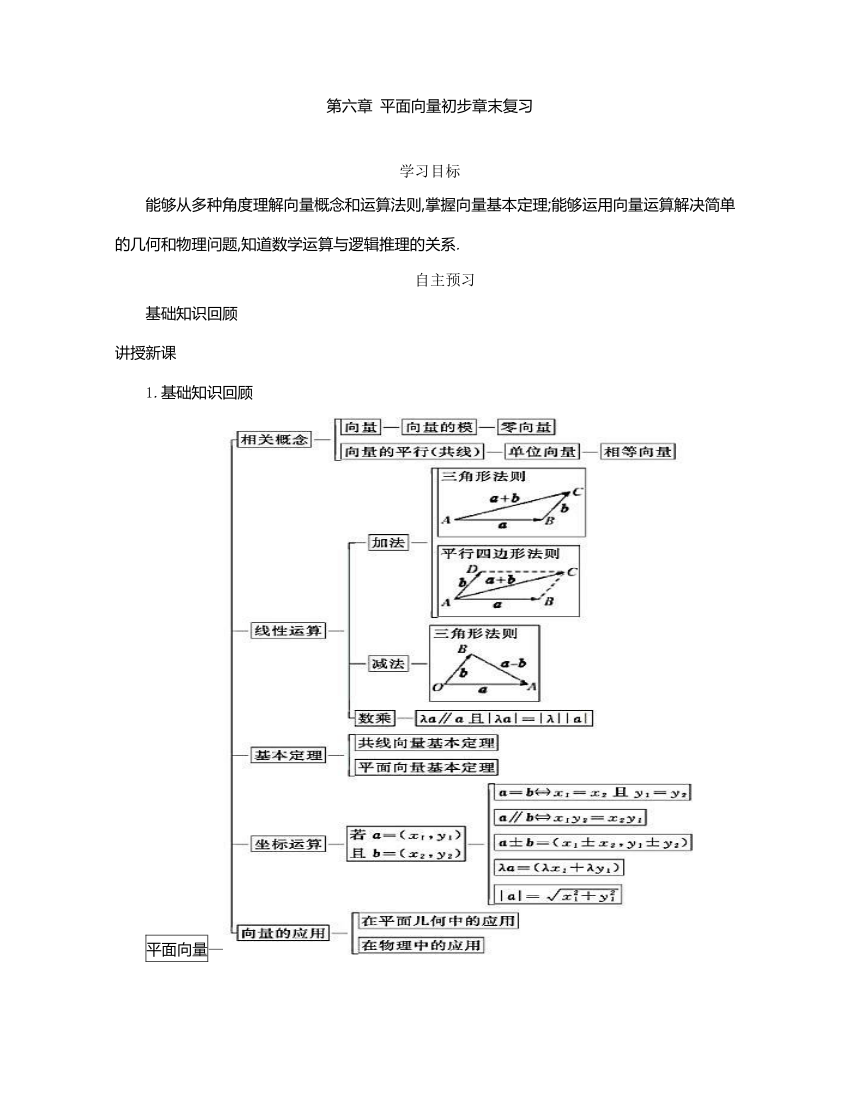
1.基础知识回顾
平面向量—
课堂探究
任务一:平面向量的有关概念
例1 给出下列命题:
①有向线段就是向量,向量就是有向线段;
②向量a与向量b平行,则a与b的方向相同或相反;
③向量与向量共线,则A,B,C,D四点共线;
④如果a∥b,b∥c,那么a∥c.
其中正确命题的个数为( )
A.1 B.2 C.3 D.0
任务二:平面向量基本定理
例2 如图所示,在△ABC中,=,P是BN上的一点,若=m+,则实数m的值为 .
例3 已知a,b是两个不共线的非零向量,且a与b起点相同,若a,tb,(a+b)三向量的终点在同一条直线上,则t= .
例4 如图,在△AOB中,D是边OB的中点,C是边OA上靠近O的三等分点,AD与BC交于M点.设=a,=b.
(1)用a,b表示;
(2)过点M的直线与边OA,OB分别交于E,F.设=p,=q,
求+的值.
任务三:平面向量坐标运算
例5 已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=λ(λ∈R),求y与λ的值.
任务四:平面向量的应用
例6 在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,则小船的行进方向应指向哪里
核心素养专练
1.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+=( )
A. B. C. D.
2.如图所示,下列结论正确的是 ( )
①=a+b;②=a-b;③=a-b;④=a+b.
A.①② B.③④ C.①③ D.②④
3.设a,b都是非零向量,下列四个条件中,使=成立的条件是( )
A.|a|=|b|且a∥b B.a=-b
C.a∥b D.a=2b
4.设向量=(k,12),=(4,5),=(10,k),求当k为何值时,A,B,C三点共线.
参考答案
自主预习
略
课堂探究
例1:D 例2: 例3:
例4:
【解】 (1)设=xa+yb,
则=-=(x-1)+y=(x-1)a+yb,=-=-a+b;
因为A,M,D三点共线,所以,共线,从而(x-1)=-y①,
又C,M,B三点共线,所以,共线,同理可得(y-1)=-x②,
联立①②,解得故=a+b.
(2)因为=-=a+b-pa=a+b.
=-=qb-pa.
因为,共线,所以q=-p,整理得+=5.
例5:
【解】(1)设点B的坐标为(x1,y1).
∵=(4,3),A(-1,-2),∴(x1+1,y1+2)=(4,3),
∴∴
∴B(3,1).同理可得D(-4,-3).
设线段BD的中点M的坐标为(x2,y2),
则x2==-,y2==-1,
∴M.
(2)由已知得=(3,1)-(2,y)=(1,1-y),
=(-4,-3)-(3,1)=(-7,-4).
又=λ,∴(1,1-y)=λ(-7,-4),
则∴
例6:
【解】如图所示,设向量的长度和方向表示水流速度的大小和方向,向量的长度和方向表示船在静水中速度的大小和方向,以,为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
核心素养专练
1.A 2.C 3.D
4.【解】若A,B,C三点共线,则,共线,则存在实数λ,使得=λ,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k,-7)=λ(10-k,k-12),
即解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
学习目标
能够从多种角度理解向量概念和运算法则,掌握向量基本定理;能够运用向量运算解决简单的几何和物理问题,知道数学运算与逻辑推理的关系.
自主预习
基础知识回顾
讲授新课
1.基础知识回顾
平面向量—
课堂探究
任务一:平面向量的有关概念
例1 给出下列命题:
①有向线段就是向量,向量就是有向线段;
②向量a与向量b平行,则a与b的方向相同或相反;
③向量与向量共线,则A,B,C,D四点共线;
④如果a∥b,b∥c,那么a∥c.
其中正确命题的个数为( )
A.1 B.2 C.3 D.0
任务二:平面向量基本定理
例2 如图所示,在△ABC中,=,P是BN上的一点,若=m+,则实数m的值为 .
例3 已知a,b是两个不共线的非零向量,且a与b起点相同,若a,tb,(a+b)三向量的终点在同一条直线上,则t= .
例4 如图,在△AOB中,D是边OB的中点,C是边OA上靠近O的三等分点,AD与BC交于M点.设=a,=b.
(1)用a,b表示;
(2)过点M的直线与边OA,OB分别交于E,F.设=p,=q,
求+的值.
任务三:平面向量坐标运算
例5 已知向量=(4,3),=(-3,-1),点A(-1,-2).
(1)求线段BD的中点M的坐标;
(2)若点P(2,y)满足=λ(λ∈R),求y与λ的值.
任务四:平面向量的应用
例6 在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,则小船的行进方向应指向哪里
核心素养专练
1.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+=( )
A. B. C. D.
2.如图所示,下列结论正确的是 ( )
①=a+b;②=a-b;③=a-b;④=a+b.
A.①② B.③④ C.①③ D.②④
3.设a,b都是非零向量,下列四个条件中,使=成立的条件是( )
A.|a|=|b|且a∥b B.a=-b
C.a∥b D.a=2b
4.设向量=(k,12),=(4,5),=(10,k),求当k为何值时,A,B,C三点共线.
参考答案
自主预习
略
课堂探究
例1:D 例2: 例3:
例4:
【解】 (1)设=xa+yb,
则=-=(x-1)+y=(x-1)a+yb,=-=-a+b;
因为A,M,D三点共线,所以,共线,从而(x-1)=-y①,
又C,M,B三点共线,所以,共线,同理可得(y-1)=-x②,
联立①②,解得故=a+b.
(2)因为=-=a+b-pa=a+b.
=-=qb-pa.
因为,共线,所以q=-p,整理得+=5.
例5:
【解】(1)设点B的坐标为(x1,y1).
∵=(4,3),A(-1,-2),∴(x1+1,y1+2)=(4,3),
∴∴
∴B(3,1).同理可得D(-4,-3).
设线段BD的中点M的坐标为(x2,y2),
则x2==-,y2==-1,
∴M.
(2)由已知得=(3,1)-(2,y)=(1,1-y),
=(-4,-3)-(3,1)=(-7,-4).
又=λ,∴(1,1-y)=λ(-7,-4),
则∴
例6:
【解】如图所示,设向量的长度和方向表示水流速度的大小和方向,向量的长度和方向表示船在静水中速度的大小和方向,以,为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
核心素养专练
1.A 2.C 3.D
4.【解】若A,B,C三点共线,则,共线,则存在实数λ,使得=λ,
因为=-=(4-k,-7),
=-=(10-k,k-12),
所以(4-k,-7)=λ(10-k,k-12),
即解得k=-2或k=11.
所以当k=-2或11时,A,B,C三点共线.
