高中数学新课标人教A版 必修五:不等关系与不等式 课件
文档属性
| 名称 | 高中数学新课标人教A版 必修五:不等关系与不等式 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 128.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-24 20:13:45 | ||
图片预览








文档简介
(共23张PPT)
课题:
3.1不等关系与不等式
教学目标:
1.知识与技能:通过具体情景,感受在现实世界和日常生活中存在着大量的不等关系,理解不等式(组)的实际背景,掌握不等式的基本性质;
2.过程与方法:通过解决具体问题,学会依据具体问题的实际背景分析问题、解决问题的方法;
3.情态与价值:通过解决具体问题,体会数学在生活中的重要作用,培养严谨的思维习惯。
教学重点 与难点:
重点:用不等式(组)表示实际问题的不等关系,并用不等式(组)研究含有不等关系的问题。理解不等式(组)对于刻画不等关系的意义和价值。两个实数比较大小的依据。
难点:用不等式(组)正确表示出不等关系。
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系,如:
1、今天的天气预报说:明天早晨最低温度为7℃,明天白天的最高温度为13℃;
2、三角形ABC的两边之和大于第三边;
3、a是一个非负实数。
在数学中,我们怎样来表示这些不等关系?
7℃≤t≤13℃
AB+AC>BC或……
a≥0
一、新课引入
4、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________
40
5、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )
v≤40
A.f ≥ 2.5%或p ≥ 2.3%
B
B.
练习:用不等式表示下面的不等关系:
1、a与b的和是非负数;
2、某公路立交桥对通过车辆的高度h“限高4m”
想一想,你还能举出哪些相似的例子
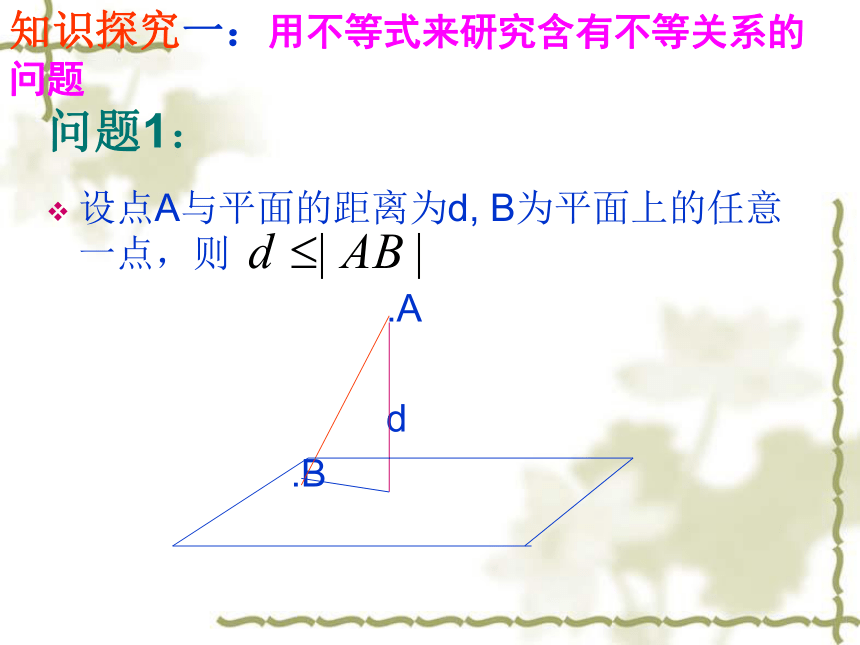
问题1:
设点A与平面的距离为d, B为平面上的任意一点,则
.A
d
.B
知识探究一:用不等式来研究含有不等关系的问题
问题2:某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
分析:若杂志的定价为x元,则销售量减少:
因此,销售总收入为:
用不等式表示为:
问题3:某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:假设截得500mm的钢管x根,截得600mm的钢管y根。根据题意,应当有什么样的不等关系呢?
(3)截得两种钢管的数量都不能为负。
(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;
(1)截得两种钢管的总长度不能超过4000mm;
上面三个不等关系,是“且”的关系,要同时满足的话,可以用下面的不等式组来表示:
考虑到实际问题的意义,还应有x, y ∈N*
x, y ∈N*
练习1:若需在长为4000mm圆钢上,截出长为698mm和518mm的两种毛坯,问怎样写出满足上述所有不等关系的不等式组?
分析:
设698mm与518mm分别x与y个
x, y ∈N*
练习2、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?
分析:设该班除小李外共有x人,这笔开学费用共y元,则:
知识探究(二):比较实数大小的基本原理
思考1:实数可以比较大小,对于两个实数a,b,其大小关系有哪几种可能?
a>b,a=b,a<b.
思考2:任何一个实数都对应数轴上的一个点,那么大数与小数所对应的点的相对位置关系如何?
大数对应的点位于小数对应的点的右边
思考3:如果两个实数的差是正数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b>0 a>b
思考4:如果两个实数的差等于零,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b=0 a=b
思考5:如果两个实数的差是负数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b<0 a<b
实数(或式)比较大小的依据是
[例1] 已知x>1,比较x3+6x与x2+6的大小.
解析:∵(x3+6x)-(x2+6)=x3-x2+6x-6
=x2(x-1)+6(x-1)=(x-1)(x2+6),
∵x>1,∴(x-1)(x2+6)>0,∴x3+6x>x2+6.
[例2] 若m>0,比较mm与2m的大小.
实数(或式)比较大小的依据是
a>b a-b>0;a=b a-b=0;a0,b>0时, >1 a>b).
方法步骤是
作差(商)——变形——判断大于或小于零(大于1或小于1).关键是变形,变形的目的在于便于判断正负.常见的变形有因式分解、配方等.
[例3] 已知a>0,试比较a与 的大小.
实数(或式)比较大小的依据是
a>b a-b>0;a=b a-b=0;a0,b>0时, >1 a>b).
方法步骤是
作差(商)——变形——判断大于或小于零(大于1或小于1).关键是变形,变形的目的在于便于判断正负.常见的变形有因式分解、配方等.
课堂小结:
1:用不等式(组)表示实际问题的不等关系,并用不等式(组)研究含有不等关系的问题。
布置作业:
课本P75习题3.1[A组]第4、5题
[B组]第1题
谢谢光临!
再见!
课题:
3.1不等关系与不等式
教学目标:
1.知识与技能:通过具体情景,感受在现实世界和日常生活中存在着大量的不等关系,理解不等式(组)的实际背景,掌握不等式的基本性质;
2.过程与方法:通过解决具体问题,学会依据具体问题的实际背景分析问题、解决问题的方法;
3.情态与价值:通过解决具体问题,体会数学在生活中的重要作用,培养严谨的思维习惯。
教学重点 与难点:
重点:用不等式(组)表示实际问题的不等关系,并用不等式(组)研究含有不等关系的问题。理解不等式(组)对于刻画不等关系的意义和价值。两个实数比较大小的依据。
难点:用不等式(组)正确表示出不等关系。
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系,如:
1、今天的天气预报说:明天早晨最低温度为7℃,明天白天的最高温度为13℃;
2、三角形ABC的两边之和大于第三边;
3、a是一个非负实数。
在数学中,我们怎样来表示这些不等关系?
7℃≤t≤13℃
AB+AC>BC或……
a≥0
一、新课引入
4、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________
40
5、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )
v≤40
A.f ≥ 2.5%或p ≥ 2.3%
B
B.
练习:用不等式表示下面的不等关系:
1、a与b的和是非负数;
2、某公路立交桥对通过车辆的高度h“限高4m”
想一想,你还能举出哪些相似的例子
问题1:
设点A与平面的距离为d, B为平面上的任意一点,则
.A
d
.B
知识探究一:用不等式来研究含有不等关系的问题
问题2:某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
分析:若杂志的定价为x元,则销售量减少:
因此,销售总收入为:
用不等式表示为:
问题3:某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:假设截得500mm的钢管x根,截得600mm的钢管y根。根据题意,应当有什么样的不等关系呢?
(3)截得两种钢管的数量都不能为负。
(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;
(1)截得两种钢管的总长度不能超过4000mm;
上面三个不等关系,是“且”的关系,要同时满足的话,可以用下面的不等式组来表示:
考虑到实际问题的意义,还应有x, y ∈N*
x, y ∈N*
练习1:若需在长为4000mm圆钢上,截出长为698mm和518mm的两种毛坯,问怎样写出满足上述所有不等关系的不等式组?
分析:
设698mm与518mm分别x与y个
x, y ∈N*
练习2、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?
分析:设该班除小李外共有x人,这笔开学费用共y元,则:
知识探究(二):比较实数大小的基本原理
思考1:实数可以比较大小,对于两个实数a,b,其大小关系有哪几种可能?
a>b,a=b,a<b.
思考2:任何一个实数都对应数轴上的一个点,那么大数与小数所对应的点的相对位置关系如何?
大数对应的点位于小数对应的点的右边
思考3:如果两个实数的差是正数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b>0 a>b
思考4:如果两个实数的差等于零,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b=0 a=b
思考5:如果两个实数的差是负数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理?
a-b<0 a<b
实数(或式)比较大小的依据是
[例1] 已知x>1,比较x3+6x与x2+6的大小.
解析:∵(x3+6x)-(x2+6)=x3-x2+6x-6
=x2(x-1)+6(x-1)=(x-1)(x2+6),
∵x>1,∴(x-1)(x2+6)>0,∴x3+6x>x2+6.
[例2] 若m>0,比较mm与2m的大小.
实数(或式)比较大小的依据是
a>b a-b>0;a=b a-b=0;a0,b>0时, >1 a>b).
方法步骤是
作差(商)——变形——判断大于或小于零(大于1或小于1).关键是变形,变形的目的在于便于判断正负.常见的变形有因式分解、配方等.
[例3] 已知a>0,试比较a与 的大小.
实数(或式)比较大小的依据是
a>b a-b>0;a=b a-b=0;a0,b>0时, >1 a>b).
方法步骤是
作差(商)——变形——判断大于或小于零(大于1或小于1).关键是变形,变形的目的在于便于判断正负.常见的变形有因式分解、配方等.
课堂小结:
1:用不等式(组)表示实际问题的不等关系,并用不等式(组)研究含有不等关系的问题。
布置作业:
课本P75习题3.1[A组]第4、5题
[B组]第1题
谢谢光临!
再见!
