全等三角形的综合应用教学设计
文档属性
| 名称 | 全等三角形的综合应用教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 85.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-25 00:00:00 | ||
图片预览

文档简介
全等三角形的综合应用
安字镇中学:王丽
[教学分析任务]
教学目标 知识技能 进一步巩固和理解全等三角形的性质与判定,能利用三角形全等解决实际问题。
数学思考 通过参与知识的探求过程,培养学生的创新意识和合作能力,
解决问题 通过探索知识过程中与同伴间的合作与交流发展有条理地思考与表达的能力。
情感态度 使学生进一步积累解决问题的经验,增强解决问题的策略意识,提高学好数学的信心。
教学重点 熟练掌握全等三角形的判定。
教学难点 把“所求问题”转化“全等三角形”问题
[教学过程设计]
问题与情景 师生行为 设计意图
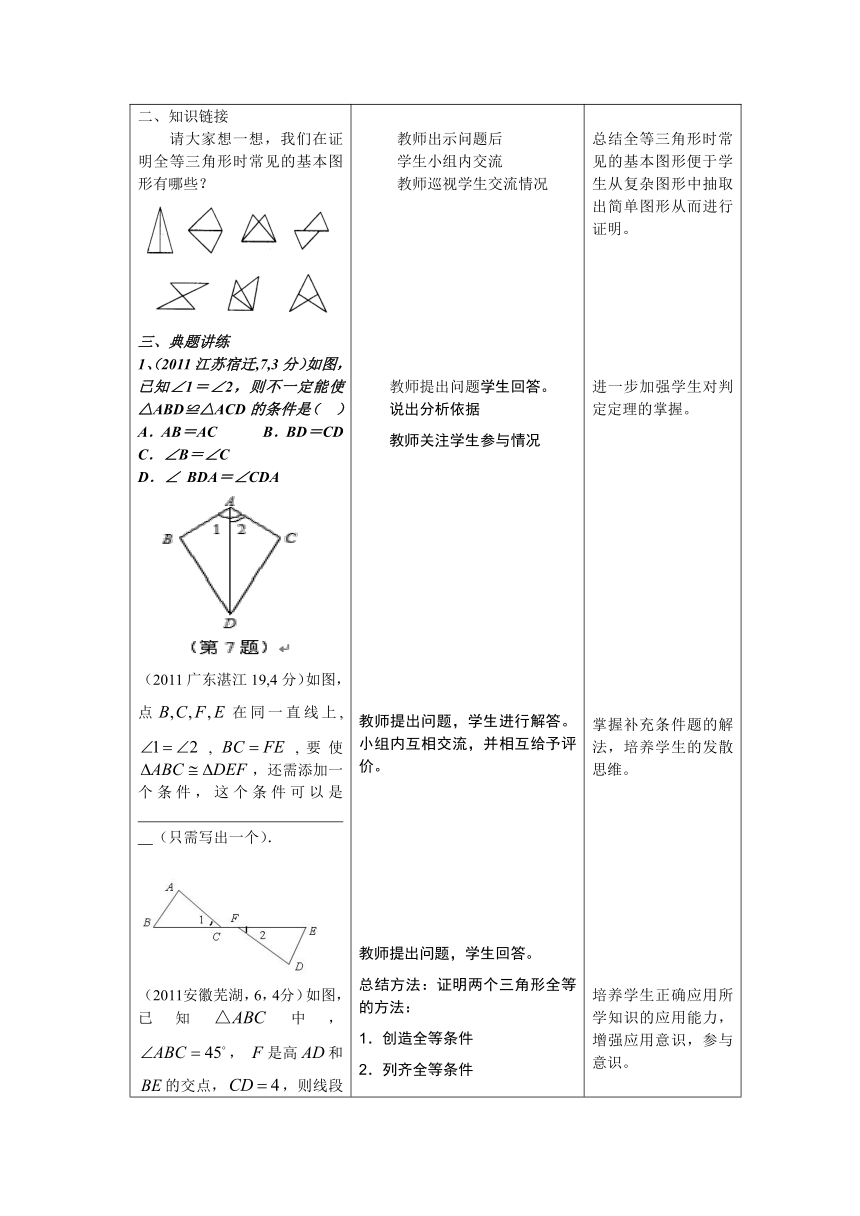
一、情境激活如图:某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是( )﹒ (A)带①和②去 (B)带①去 (C)带②去 (D)带③去 请大家想一想:“边边角”和“角角角”能判定两个三角形全等吗?二、知识链接请大家想一想,我们在证明全等三角形时常见的基本图形有哪些?三、典题讲练1、(2011江苏宿迁,7,3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )A.AB=AC B.BD=CD C.∠B=∠C D.∠ BDA=∠CDA(2011广东湛江19,4分)如图,点在同一直线上, ,,要使,还需添加一个条件,这个条件可以是 (只需写出一个).(2011安徽芜湖,6,4分)如图,已知中,, 是高和的交点,,则线段的长度为( ). A. B. 4 C. D.( 2011重庆江津, 22,10分)在△ABC中,AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数.(2007内江中考)如图, △ACB 和 △ECD 都是等腰直角三角形,A,C,D三点在同一直线上,连结BD,AE,并延长AE交BD于F.求证:△ACE≌△BCD; (2)直线AE与BD互相垂直吗?请证明你的结论.已知中,,、分别平分和,、交于点,试判断、、的数量关系,并加以证明. 四、综合拓展1、教材P23页习题11.3第6题为:如图所示,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,你能找出图中的全等三角形吗 如果再加上AB=AC呢 (1)一变:AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,AB=AC,连接EF交AD于M,你能找出图中的全等三角形吗 (2)二变:在变形(1)的基础上,当∠BAC=90°时,你能找出图中的全等三角形吗 2、如图所示,已知点C为线段AB上一点,△ACM、△BCN是等边三角形.求证:AN=BM;(1)一变:将△BCN绕点C顺时针旋转,在旋转的过程中,AN与BM在数量上有何关系?(2)二变:将原题中△BCN沿AB所在直线翻折,AN与BM在数量上有何关系?(3)三变:若把原题中“△ACM和△BCN是两个等边三角形”换成两个正方形(如图所示),AN与BM的关系如何 请说明理由.3、如图,已知中,厘米,厘米,点为的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?五、反思归纳 教师提出问题 教师在学生回答问题后教师追问你的依据是什么,教师继续提问:除了刚才所说的判定方法两个三角形全等的判定方法还有哪几种? 强调:第五种方法“HL”比较特殊,要借助直角三角形才能用。学生回答后教师利用课件演示 教师出示问题后 学生小组内交流 教师巡视学生交流情况教师提出问题学生回答。 说出分析依据 教师关注学生参与情况 教师提出问题,学生进行解答。小组内互相交流,并相互给予评价。教师提出问题,学生回答。总结方法:证明两个三角形全等的方法:1.创造全等条件2.列齐全等条件3.得出结论小结:我们又多了一种说明边(或角)相等的方法。1)关于求角度计算的有哪些方法?2)这里用哪种方法比较合适?3)全等的条件齐不齐,还缺哪些?怎样创造?教师出示问题,1)要说明两条线段垂直,有哪些方法?2)这里用哪种方法比较合适?3)全等的条件齐不齐,还缺哪些?怎样创造?教师出示问题后,学生观察图形进行猜想。然后小组内进行交流,探究解决问题的途径。教师在学生中进行巡视。在学生解决有困难时,教师启发引导学生得出辅助线做法。截长补短构造全等三角形。教师出示课本练习题,学生解答。教师在学生解答后变换已知条件。体会条件增加的情况下,全等三角形的数量会增加,且全等三角形具有传递性。教师出示问题分析:要说明两条线段相等,只要先说明两个三角形全等。找出这两条线段分别在哪两个三角形中,全等的条件够吗?(学生完成过程)学生在教师的引导启发下在思考并解决问题。写出解题步骤。教师变换图形,学生思考后解答。解题后学生观察变化后的图形及解题步骤,总结解法。 教师出示问题学生思考在学生解题有困难时,教师可启发学生,题中是在什么情况下求证两个三角形全等,此时具备哪些已知条件?教师启发引导(2)中在运动过程中点P与点Q是在什么情况下第一次相遇的,此时两者在运动过程中要满足什么条件?教师与学生共同回顾应用,归纳常用辅助线的添加方法。 利用简单的实际问题的解决,激发学生的学习兴趣。复习三角形全等的判定方法为后续学习做好铺垫。 对对学生的易错点进行强调总结全等三角形时常见的基本图形便于学生从复杂图形中抽取出简单图形从而进行证明。进一步加强学生对判定定理的掌握。掌握补充条件题的解法,培养学生的发散思维。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识,提高与他人合作与交流的能力。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识,培养学生的逻辑思维能力。培养学生的创新意识和实践能力。通过学生的观察,经历从复杂图形中抽出全等三角形,培养学生的观察能力、空间想象能力,端正严谨的学习态度。在解题过程中,提高学生的逻辑推理能力和语言表达能力。掌握变换条件下解题的方法,培养变换条件下解题的能力。动点问题是中考的热点问题,而对学生来说也是难点问题。使学生掌握化动点为静点,化难为易的解题方法。向学生渗透转化的思想。总结回顾学习内容,帮助学生归纳。
A
B
C
E
F
第2△ABC2题图
A
Q
C
D
B
P
安字镇中学:王丽
[教学分析任务]
教学目标 知识技能 进一步巩固和理解全等三角形的性质与判定,能利用三角形全等解决实际问题。
数学思考 通过参与知识的探求过程,培养学生的创新意识和合作能力,
解决问题 通过探索知识过程中与同伴间的合作与交流发展有条理地思考与表达的能力。
情感态度 使学生进一步积累解决问题的经验,增强解决问题的策略意识,提高学好数学的信心。
教学重点 熟练掌握全等三角形的判定。
教学难点 把“所求问题”转化“全等三角形”问题
[教学过程设计]
问题与情景 师生行为 设计意图
一、情境激活如图:某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是( )﹒ (A)带①和②去 (B)带①去 (C)带②去 (D)带③去 请大家想一想:“边边角”和“角角角”能判定两个三角形全等吗?二、知识链接请大家想一想,我们在证明全等三角形时常见的基本图形有哪些?三、典题讲练1、(2011江苏宿迁,7,3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )A.AB=AC B.BD=CD C.∠B=∠C D.∠ BDA=∠CDA(2011广东湛江19,4分)如图,点在同一直线上, ,,要使,还需添加一个条件,这个条件可以是 (只需写出一个).(2011安徽芜湖,6,4分)如图,已知中,, 是高和的交点,,则线段的长度为( ). A. B. 4 C. D.( 2011重庆江津, 22,10分)在△ABC中,AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数.(2007内江中考)如图, △ACB 和 △ECD 都是等腰直角三角形,A,C,D三点在同一直线上,连结BD,AE,并延长AE交BD于F.求证:△ACE≌△BCD; (2)直线AE与BD互相垂直吗?请证明你的结论.已知中,,、分别平分和,、交于点,试判断、、的数量关系,并加以证明. 四、综合拓展1、教材P23页习题11.3第6题为:如图所示,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,你能找出图中的全等三角形吗 如果再加上AB=AC呢 (1)一变:AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,AB=AC,连接EF交AD于M,你能找出图中的全等三角形吗 (2)二变:在变形(1)的基础上,当∠BAC=90°时,你能找出图中的全等三角形吗 2、如图所示,已知点C为线段AB上一点,△ACM、△BCN是等边三角形.求证:AN=BM;(1)一变:将△BCN绕点C顺时针旋转,在旋转的过程中,AN与BM在数量上有何关系?(2)二变:将原题中△BCN沿AB所在直线翻折,AN与BM在数量上有何关系?(3)三变:若把原题中“△ACM和△BCN是两个等边三角形”换成两个正方形(如图所示),AN与BM的关系如何 请说明理由.3、如图,已知中,厘米,厘米,点为的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?五、反思归纳 教师提出问题 教师在学生回答问题后教师追问你的依据是什么,教师继续提问:除了刚才所说的判定方法两个三角形全等的判定方法还有哪几种? 强调:第五种方法“HL”比较特殊,要借助直角三角形才能用。学生回答后教师利用课件演示 教师出示问题后 学生小组内交流 教师巡视学生交流情况教师提出问题学生回答。 说出分析依据 教师关注学生参与情况 教师提出问题,学生进行解答。小组内互相交流,并相互给予评价。教师提出问题,学生回答。总结方法:证明两个三角形全等的方法:1.创造全等条件2.列齐全等条件3.得出结论小结:我们又多了一种说明边(或角)相等的方法。1)关于求角度计算的有哪些方法?2)这里用哪种方法比较合适?3)全等的条件齐不齐,还缺哪些?怎样创造?教师出示问题,1)要说明两条线段垂直,有哪些方法?2)这里用哪种方法比较合适?3)全等的条件齐不齐,还缺哪些?怎样创造?教师出示问题后,学生观察图形进行猜想。然后小组内进行交流,探究解决问题的途径。教师在学生中进行巡视。在学生解决有困难时,教师启发引导学生得出辅助线做法。截长补短构造全等三角形。教师出示课本练习题,学生解答。教师在学生解答后变换已知条件。体会条件增加的情况下,全等三角形的数量会增加,且全等三角形具有传递性。教师出示问题分析:要说明两条线段相等,只要先说明两个三角形全等。找出这两条线段分别在哪两个三角形中,全等的条件够吗?(学生完成过程)学生在教师的引导启发下在思考并解决问题。写出解题步骤。教师变换图形,学生思考后解答。解题后学生观察变化后的图形及解题步骤,总结解法。 教师出示问题学生思考在学生解题有困难时,教师可启发学生,题中是在什么情况下求证两个三角形全等,此时具备哪些已知条件?教师启发引导(2)中在运动过程中点P与点Q是在什么情况下第一次相遇的,此时两者在运动过程中要满足什么条件?教师与学生共同回顾应用,归纳常用辅助线的添加方法。 利用简单的实际问题的解决,激发学生的学习兴趣。复习三角形全等的判定方法为后续学习做好铺垫。 对对学生的易错点进行强调总结全等三角形时常见的基本图形便于学生从复杂图形中抽取出简单图形从而进行证明。进一步加强学生对判定定理的掌握。掌握补充条件题的解法,培养学生的发散思维。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识,提高与他人合作与交流的能力。培养学生正确应用所学知识的应用能力,增强应用意识,参与意识,培养学生的逻辑思维能力。培养学生的创新意识和实践能力。通过学生的观察,经历从复杂图形中抽出全等三角形,培养学生的观察能力、空间想象能力,端正严谨的学习态度。在解题过程中,提高学生的逻辑推理能力和语言表达能力。掌握变换条件下解题的方法,培养变换条件下解题的能力。动点问题是中考的热点问题,而对学生来说也是难点问题。使学生掌握化动点为静点,化难为易的解题方法。向学生渗透转化的思想。总结回顾学习内容,帮助学生归纳。
A
B
C
E
F
第2△ABC2题图
A
Q
C
D
B
P
