苏科版八年级数学上册 1.2 全等三角形(表格式教案)
文档属性
| 名称 | 苏科版八年级数学上册 1.2 全等三角形(表格式教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 106.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览

文档简介
课题:全等三角形
教学目标 ①通过实例理解全等形的概念和特征,并能识别图形的全等. ②知道全等三角形的有关概念,能正确地找出对应顶点、对应边、对应角;掌握全等三角形对应边相等,对应角相等的性质. ③通过两个重合的三角形变换其中一个的位置,使它们呈现各种不同位置的活动,让学生从中了解并体会图形变换的思想,逐步培养学生动态的研究几何图形的意识.
教学重点 全等三角形的有关概念和性质.
教学难点 理解全等三角形边、角之间的对应关系.
教学方法 引导探究
教学手段 多媒体课件
教 学 过 程
教学环节 教 师 活 动 学生活动 设 计 意 图
一、情境导入 (一)操作引入 1、观察下列同一组的两个图形有什么特点? 我们把能完全重合的图形叫全等图形. 一个图形经过平移、旋转、翻折后得到的新图形与原图形全等. 2、请同学们剪两个能重合的三角形。 问怎样的两个三角形叫全等的三角形? 以全等形引入全等三角形,实现知识迁移。
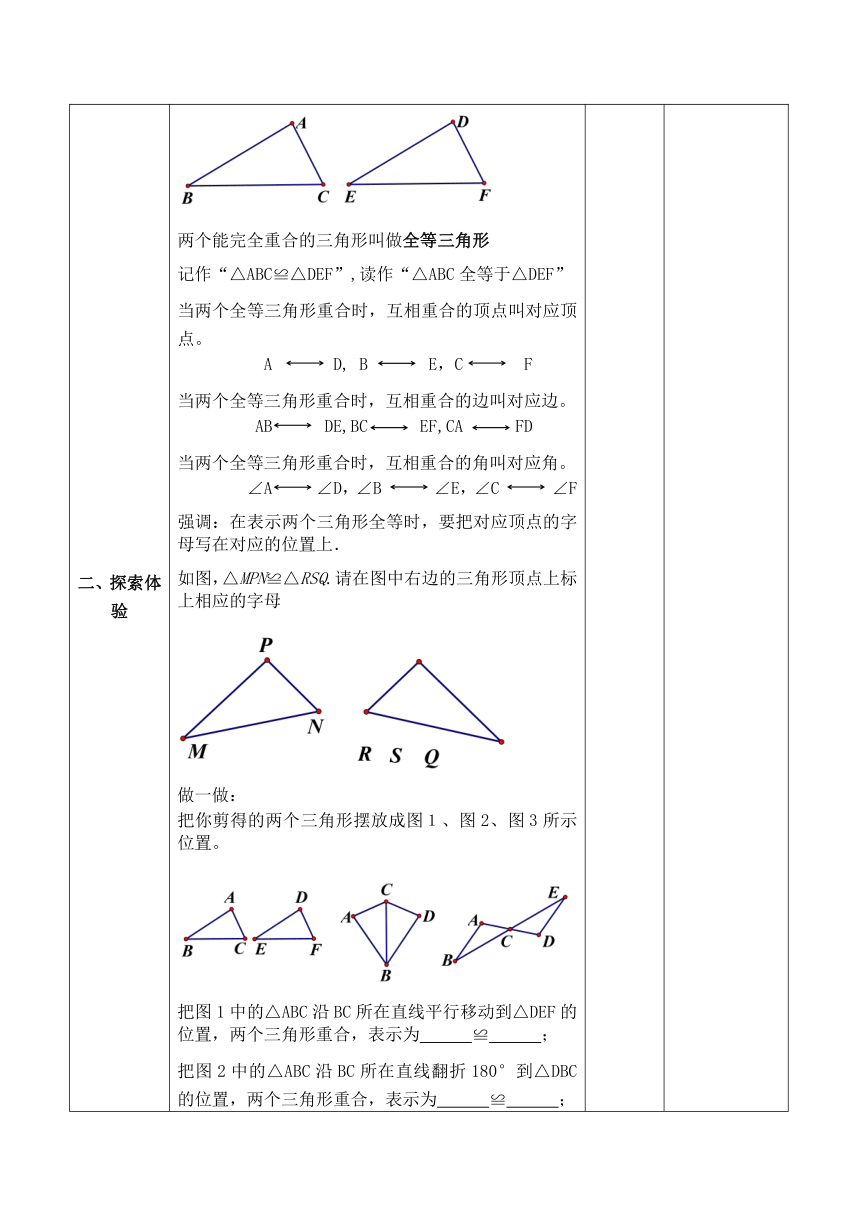
二、探索体验 两个能完全重合的三角形叫做全等三角形 记作“△ABC≌△DEF”,读作“△ABC全等于△DEF” 当两个全等三角形重合时,互相重合的顶点叫对应顶点。 A D, B E,C F 当两个全等三角形重合时,互相重合的边叫对应边。 AB DE,BC EF,CA FD 当两个全等三角形重合时,互相重合的角叫对应角。 ∠A ∠D,∠B ∠E,∠C ∠F 强调:在表示两个三角形全等时,要把对应顶点的字母写在对应的位置上. 如图,△MPN≌△RSQ.请在图中右边的三角形顶点上标上相应的字母 做一做: 把你剪得的两个三角形摆放成图1、图2、图3所示位置。 把图1中的△ABC沿BC所在直线平行移动到△DEF的位置,两个三角形重合,表示为 ≌ ; 把图2中的△ABC沿BC所在直线翻折180°到△DBC的位置,两个三角形重合,表示为 ≌ ;
把图3中的△ABC绕顶点C旋转180°到△DEC的位置,两个三角形重合,表示为 ≌ ; 做一做之后还可添加下列几种图形 图中的△AED是由△ABC(或△CAB)经过怎样的变换而得到的?并用你剪得的三角形操作演示,以验证你的结论。 全等三角形的对应边相等,对应角全等. ∵△ABC≌ △DEF ∴ AB=DE, BC=EF, AC=DF (全等三角形的对应边相等) ∴ ∠ A= ∠ D, ∠ B= ∠ E , ∠ C= ∠ F (全等三角形的对应角相等) 练习:如果△ABC ≌ △CDA,∠B =70°, AB =3cm, 那么∠D =____,DC =____cm 变式:如右图,若再加条件CF=2 cm ,则AE= cm. 通过学生自主探究发现规律、验证规律,提高学生的学习能力。
三、巩固提高 1.如图:△ABC≌△ABD,用等式写出这两个三角形的对应边和对应角。 2. 如图:已知△ABD≌△ACE,用等式写出两个三角形的对应边和对应角。 练一练:
找出下列图中一对全等三角形,并用符号语言表达。 练一练:
找出下列图中两对全等三角形,并用符号语言表达。 变式:见右图,图中有几对全等三角形? 独立思考后, 讨论合作完成。 让学生通过练习加深对全等三角形的认识
四、收获体会 1、回忆这节课,学习了全等三角形的哪些知识? 全等三角形的概念、性质、表示方法、对应写法 2、找全等三角形对应边、对应角的方法 若知道全等符号,利用对应位置即可. 从动态的角度来看:平移、翻折、旋转。 从静态的角度来看: (1)大边对应大边,大角对应大角 (2)公共边是对应边,公共角是对应角 (3)对应边所对的角是对应角,对应角所对的边是对应边 回忆叙述,畅谈交流
五、拓展与延伸 1.议一议:右图是一个等边三角形, 你能把它分成两个全等的三角形吗 你能把它分成三个、四个、六个全等的三 角形吗 课后完成
教学设计说明:
1.关于全等三角形概念的教学设计:①类比全等图形的概念(类比具有很大的教育价值,因为通过对象之间的类比,可以由一个解释另一个,从而使学生产生兴趣,使人信服,并能形成抽象的想象能力。)
②自己先做一对互相重合的三角形,看着实例说概念。(从具体到抽象,可以化解难点,有利于理解掌握。)
③给出一对三角形,问我们如何判断它们是否全等,利用定义来验证。(定义具有双重属性,既是性质又是判定。)
2.关于全等三角形性质的教学设计:注重三种语言(文字,符号,图形)的对照,从不同的侧面来表达同一个东西,使学生对全等三角形的性质的理解全面和透彻。
3.关于正确识别全等三角形的教学设计:经历三角形的平移、翻折、旋转变换的过程,在活动过程中体会并理解平移、翻折、旋转变换的本质,按照“操作—观察—作答”顺序进行。使学生了解用图形变换识别全等三角形的方法,突破难点。
4.关于巩固与提高的教学设计:按照由易到难,先巩固再提高的顺序安排。先是直接的两个三角形全等,然后是在比较复杂的图形中找三角形全等,最后在等边三角形中构造全等三角形。学习过程的一个明显的特性是思想在不断的活动,但其间有着相对的层次,让不同层次的学生都能得到相应的发展。
教学目标 ①通过实例理解全等形的概念和特征,并能识别图形的全等. ②知道全等三角形的有关概念,能正确地找出对应顶点、对应边、对应角;掌握全等三角形对应边相等,对应角相等的性质. ③通过两个重合的三角形变换其中一个的位置,使它们呈现各种不同位置的活动,让学生从中了解并体会图形变换的思想,逐步培养学生动态的研究几何图形的意识.
教学重点 全等三角形的有关概念和性质.
教学难点 理解全等三角形边、角之间的对应关系.
教学方法 引导探究
教学手段 多媒体课件
教 学 过 程
教学环节 教 师 活 动 学生活动 设 计 意 图
一、情境导入 (一)操作引入 1、观察下列同一组的两个图形有什么特点? 我们把能完全重合的图形叫全等图形. 一个图形经过平移、旋转、翻折后得到的新图形与原图形全等. 2、请同学们剪两个能重合的三角形。 问怎样的两个三角形叫全等的三角形? 以全等形引入全等三角形,实现知识迁移。
二、探索体验 两个能完全重合的三角形叫做全等三角形 记作“△ABC≌△DEF”,读作“△ABC全等于△DEF” 当两个全等三角形重合时,互相重合的顶点叫对应顶点。 A D, B E,C F 当两个全等三角形重合时,互相重合的边叫对应边。 AB DE,BC EF,CA FD 当两个全等三角形重合时,互相重合的角叫对应角。 ∠A ∠D,∠B ∠E,∠C ∠F 强调:在表示两个三角形全等时,要把对应顶点的字母写在对应的位置上. 如图,△MPN≌△RSQ.请在图中右边的三角形顶点上标上相应的字母 做一做: 把你剪得的两个三角形摆放成图1、图2、图3所示位置。 把图1中的△ABC沿BC所在直线平行移动到△DEF的位置,两个三角形重合,表示为 ≌ ; 把图2中的△ABC沿BC所在直线翻折180°到△DBC的位置,两个三角形重合,表示为 ≌ ;
把图3中的△ABC绕顶点C旋转180°到△DEC的位置,两个三角形重合,表示为 ≌ ; 做一做之后还可添加下列几种图形 图中的△AED是由△ABC(或△CAB)经过怎样的变换而得到的?并用你剪得的三角形操作演示,以验证你的结论。 全等三角形的对应边相等,对应角全等. ∵△ABC≌ △DEF ∴ AB=DE, BC=EF, AC=DF (全等三角形的对应边相等) ∴ ∠ A= ∠ D, ∠ B= ∠ E , ∠ C= ∠ F (全等三角形的对应角相等) 练习:如果△ABC ≌ △CDA,∠B =70°, AB =3cm, 那么∠D =____,DC =____cm 变式:如右图,若再加条件CF=2 cm ,则AE= cm. 通过学生自主探究发现规律、验证规律,提高学生的学习能力。
三、巩固提高 1.如图:△ABC≌△ABD,用等式写出这两个三角形的对应边和对应角。 2. 如图:已知△ABD≌△ACE,用等式写出两个三角形的对应边和对应角。 练一练:
找出下列图中一对全等三角形,并用符号语言表达。 练一练:
找出下列图中两对全等三角形,并用符号语言表达。 变式:见右图,图中有几对全等三角形? 独立思考后, 讨论合作完成。 让学生通过练习加深对全等三角形的认识
四、收获体会 1、回忆这节课,学习了全等三角形的哪些知识? 全等三角形的概念、性质、表示方法、对应写法 2、找全等三角形对应边、对应角的方法 若知道全等符号,利用对应位置即可. 从动态的角度来看:平移、翻折、旋转。 从静态的角度来看: (1)大边对应大边,大角对应大角 (2)公共边是对应边,公共角是对应角 (3)对应边所对的角是对应角,对应角所对的边是对应边 回忆叙述,畅谈交流
五、拓展与延伸 1.议一议:右图是一个等边三角形, 你能把它分成两个全等的三角形吗 你能把它分成三个、四个、六个全等的三 角形吗 课后完成
教学设计说明:
1.关于全等三角形概念的教学设计:①类比全等图形的概念(类比具有很大的教育价值,因为通过对象之间的类比,可以由一个解释另一个,从而使学生产生兴趣,使人信服,并能形成抽象的想象能力。)
②自己先做一对互相重合的三角形,看着实例说概念。(从具体到抽象,可以化解难点,有利于理解掌握。)
③给出一对三角形,问我们如何判断它们是否全等,利用定义来验证。(定义具有双重属性,既是性质又是判定。)
2.关于全等三角形性质的教学设计:注重三种语言(文字,符号,图形)的对照,从不同的侧面来表达同一个东西,使学生对全等三角形的性质的理解全面和透彻。
3.关于正确识别全等三角形的教学设计:经历三角形的平移、翻折、旋转变换的过程,在活动过程中体会并理解平移、翻折、旋转变换的本质,按照“操作—观察—作答”顺序进行。使学生了解用图形变换识别全等三角形的方法,突破难点。
4.关于巩固与提高的教学设计:按照由易到难,先巩固再提高的顺序安排。先是直接的两个三角形全等,然后是在比较复杂的图形中找三角形全等,最后在等边三角形中构造全等三角形。学习过程的一个明显的特性是思想在不断的活动,但其间有着相对的层次,让不同层次的学生都能得到相应的发展。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
