苏科版八年级数学上册 3.1 勾股定理(教案)
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 733.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 00:00:00 | ||
图片预览


文档简介
课题:3.1 勾股定理教案
教学目标:
1、体验勾股定理的探索过程,培养观察、猜想、分析和概括的能力。
2、掌握勾股定理的内容,并运用勾股定理解决简单的实际问题。
教学重点:勾股定理的探索与生成
教学难点:勾股定理的探索与准确运用
教学过程:
情境引入
(1)淮安市正在“创建文明城市”,作为一名中学生,我们应该为创卫工作献出自己的一份力量。从身边小事做起,杜绝不文明!
“杜绝不文明”:有同学穿过一个如图所示的草坪走“近道”,真的少走了很远吗?带着这个问题一起来学习今天的内容!
(
8m
6m
C
B
A
草地
)
(2)数学小故事地板中的勾股图
话说一天毕达哥拉斯去朋友家做客,发现地板上的几何图形非常漂亮,他就观察起来,并用笔在地板上画了起来,并由此发现了一个非常伟大的定理,人们为了纪念他,发行了这张美丽的邮票。
毕达哥拉斯究竟发现了什么呢?让我们一起跟着他的脚印,一起来学习。
1955年希腊为纪念数学家毕达哥拉斯发行的邮票。
二、新课讲解
(1)探究活动1:
邮票赏析观察这枚邮票上的图案,回答问题:
①图案中有哪些图形?
②数一数图案中三个正方形内的小方格个数从小到大依次为________,________,_______;
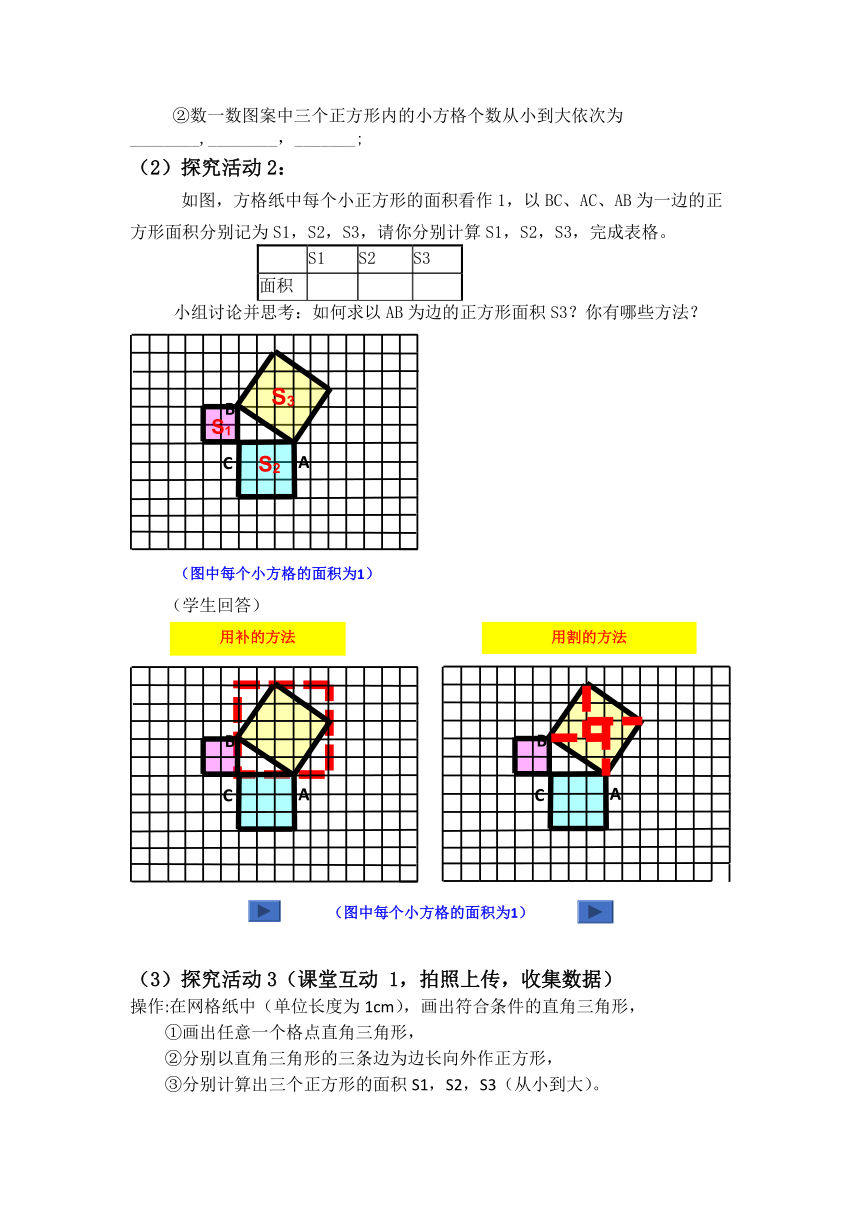
(2)探究活动2:
如图,方格纸中每个小正方形的面积看作1,以BC、AC、AB为一边的正方形面积分别记为S1,S2,S3,请你分别计算S1,S2,S3,完成表格。
S1 S2 S3
面积
小组讨论并思考:如何求以AB为边的正方形面积S3?你有哪些方法? (
C
B
A
(图中每个小方格的面积为
1
)
S
1
S
2
S
3
)
(学生回答)
(
C
B
A
C
B
A
用补的方法
用割的方法
(图中每个小方格的面积为
1
)
)
(3)探究活动3(课堂互动 1,拍照上传,收集数据)
操作:在网格纸中(单位长度为1cm),画出符合条件的直角三角形,
①画出任意一个格点直角三角形,
②分别以直角三角形的三条边为边长向外作正方形,
③分别计算出三个正方形的面积S1,S2,S3(从小到大)。
S1 S2 S3
正方形面积
发现:
统计学生数据:
三角形 S1 S2 S3 猜想:面积关系
直角三角形 邮票 9 16 25 (
S
1
+S
2
=S
3
)
活动 4 9 13
图1
图2
图3
图4
(4)验证1:刚才所选取的直角三角形都放置在网格中,且两直角边长度都为整数,下面老师用几何画板演示一下各边为任意一个数值的情况。(几何画板演示)
(5)验证2: 实验法(几何画板演示)
(6)归纳总结
如果直角三角形的两直角边的长分别为a和b,斜边长为c ,
①.用a,b,c来表示这3个正方形的面积。
②你能发现直角三角形三边长度之间存在什么关系吗?
③你能用文字语言描述吗?
勾股定理 :直角三角形两直角边a、b的平方和等于斜边c的平方。
(
a
b
c
B
C
A
)
几何语言:在Rt△ ABC中,∠C=90°
则
或 BC2+AC2=AB2
(7)勾股知识
1、你知道为什么称为勾股定理吗?
(
弦
)古人把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
(
勾
) (
勾
)
(
股
) (
股
)
2、勾股史话
我国是最早了解勾股定理的国家之一. 早在三千多年前,周朝的数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”. 它被记载于我国古代著名的数学著作《周髀算经》中. 在这本书中的另一处,还记载了勾股定理的一般形式. 这一发现,至少早于古希腊人500多年. 作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
(8)验证3:面积法
三、课堂练习
1、根据下列图中正方形的面积,写出表示边的未知数x、y的值。(思考后抢答)
x= y=
2、求下列直角三角形中未知边的长。(课堂互动2,拍照上传)
3、如图,受台风影响,一棵树在离地面3米处断裂,树的顶部落在离树跟底部4米处,这棵树折断前有多高?(课堂互动3,拍照上传)
(
3
米
4
米
)
当堂检测(课堂互动4,平板当堂反馈)
五、回归情境 “爱护环境 人人有责” 小明实际上只少走了几米的距离?
六、拓展:
在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的面积为9cm2,则正方形a,b的面积之和是 cm .
若最大正方形的面积为9cm2,则正方形c,d,e,f的面积之和是 cm .
(
a
f
c
d
e
b
)
七、欣赏数学之美
美丽的勾股树
愿所有同学在生活中像毕达哥拉斯一样,,善于观察,善于发现不断地充实自己,让自己成长为一棵参天大树!
八、课堂小结:我有哪些收获呢?与大家共分享!
教学目标:
1、体验勾股定理的探索过程,培养观察、猜想、分析和概括的能力。
2、掌握勾股定理的内容,并运用勾股定理解决简单的实际问题。
教学重点:勾股定理的探索与生成
教学难点:勾股定理的探索与准确运用
教学过程:
情境引入
(1)淮安市正在“创建文明城市”,作为一名中学生,我们应该为创卫工作献出自己的一份力量。从身边小事做起,杜绝不文明!
“杜绝不文明”:有同学穿过一个如图所示的草坪走“近道”,真的少走了很远吗?带着这个问题一起来学习今天的内容!
(
8m
6m
C
B
A
草地
)
(2)数学小故事地板中的勾股图
话说一天毕达哥拉斯去朋友家做客,发现地板上的几何图形非常漂亮,他就观察起来,并用笔在地板上画了起来,并由此发现了一个非常伟大的定理,人们为了纪念他,发行了这张美丽的邮票。
毕达哥拉斯究竟发现了什么呢?让我们一起跟着他的脚印,一起来学习。
1955年希腊为纪念数学家毕达哥拉斯发行的邮票。
二、新课讲解
(1)探究活动1:
邮票赏析观察这枚邮票上的图案,回答问题:
①图案中有哪些图形?
②数一数图案中三个正方形内的小方格个数从小到大依次为________,________,_______;
(2)探究活动2:
如图,方格纸中每个小正方形的面积看作1,以BC、AC、AB为一边的正方形面积分别记为S1,S2,S3,请你分别计算S1,S2,S3,完成表格。
S1 S2 S3
面积
小组讨论并思考:如何求以AB为边的正方形面积S3?你有哪些方法? (
C
B
A
(图中每个小方格的面积为
1
)
S
1
S
2
S
3
)
(学生回答)
(
C
B
A
C
B
A
用补的方法
用割的方法
(图中每个小方格的面积为
1
)
)
(3)探究活动3(课堂互动 1,拍照上传,收集数据)
操作:在网格纸中(单位长度为1cm),画出符合条件的直角三角形,
①画出任意一个格点直角三角形,
②分别以直角三角形的三条边为边长向外作正方形,
③分别计算出三个正方形的面积S1,S2,S3(从小到大)。
S1 S2 S3
正方形面积
发现:
统计学生数据:
三角形 S1 S2 S3 猜想:面积关系
直角三角形 邮票 9 16 25 (
S
1
+S
2
=S
3
)
活动 4 9 13
图1
图2
图3
图4
(4)验证1:刚才所选取的直角三角形都放置在网格中,且两直角边长度都为整数,下面老师用几何画板演示一下各边为任意一个数值的情况。(几何画板演示)
(5)验证2: 实验法(几何画板演示)
(6)归纳总结
如果直角三角形的两直角边的长分别为a和b,斜边长为c ,
①.用a,b,c来表示这3个正方形的面积。
②你能发现直角三角形三边长度之间存在什么关系吗?
③你能用文字语言描述吗?
勾股定理 :直角三角形两直角边a、b的平方和等于斜边c的平方。
(
a
b
c
B
C
A
)
几何语言:在Rt△ ABC中,∠C=90°
则
或 BC2+AC2=AB2
(7)勾股知识
1、你知道为什么称为勾股定理吗?
(
弦
)古人把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
(
勾
) (
勾
)
(
股
) (
股
)
2、勾股史话
我国是最早了解勾股定理的国家之一. 早在三千多年前,周朝的数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”. 它被记载于我国古代著名的数学著作《周髀算经》中. 在这本书中的另一处,还记载了勾股定理的一般形式. 这一发现,至少早于古希腊人500多年. 作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
(8)验证3:面积法
三、课堂练习
1、根据下列图中正方形的面积,写出表示边的未知数x、y的值。(思考后抢答)
x= y=
2、求下列直角三角形中未知边的长。(课堂互动2,拍照上传)
3、如图,受台风影响,一棵树在离地面3米处断裂,树的顶部落在离树跟底部4米处,这棵树折断前有多高?(课堂互动3,拍照上传)
(
3
米
4
米
)
当堂检测(课堂互动4,平板当堂反馈)
五、回归情境 “爱护环境 人人有责” 小明实际上只少走了几米的距离?
六、拓展:
在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的面积为9cm2,则正方形a,b的面积之和是 cm .
若最大正方形的面积为9cm2,则正方形c,d,e,f的面积之和是 cm .
(
a
f
c
d
e
b
)
七、欣赏数学之美
美丽的勾股树
愿所有同学在生活中像毕达哥拉斯一样,,善于观察,善于发现不断地充实自己,让自己成长为一棵参天大树!
八、课堂小结:我有哪些收获呢?与大家共分享!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
