苏科版八年级数学上册 6.1 函数 第去课时(教案)
文档属性
| 名称 | 苏科版八年级数学上册 6.1 函数 第去课时(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 19:06:33 | ||
图片预览

文档简介
课题 6.1函数(1)
学习目标 1.通过简单实例,了解常量与变量的意义; 2.通过实例,让学生多角度、多层面地认识和理解函数的意义,感受函数的多种表示形式; 3.能说出一些函数的实例,并能判断两个变量间的关系是否是函数关系。
重点难点 重点:函数概念的建立;判断两个变量间的关系是否是函数关系。 难点:函数概念中的常量、变量的理解及其对应关系探索。
学习过程
情景激活 情境导入: “变化”引领我们去探索新知识,这节课就让我们在变化过程中去感悟新的领域——函数。
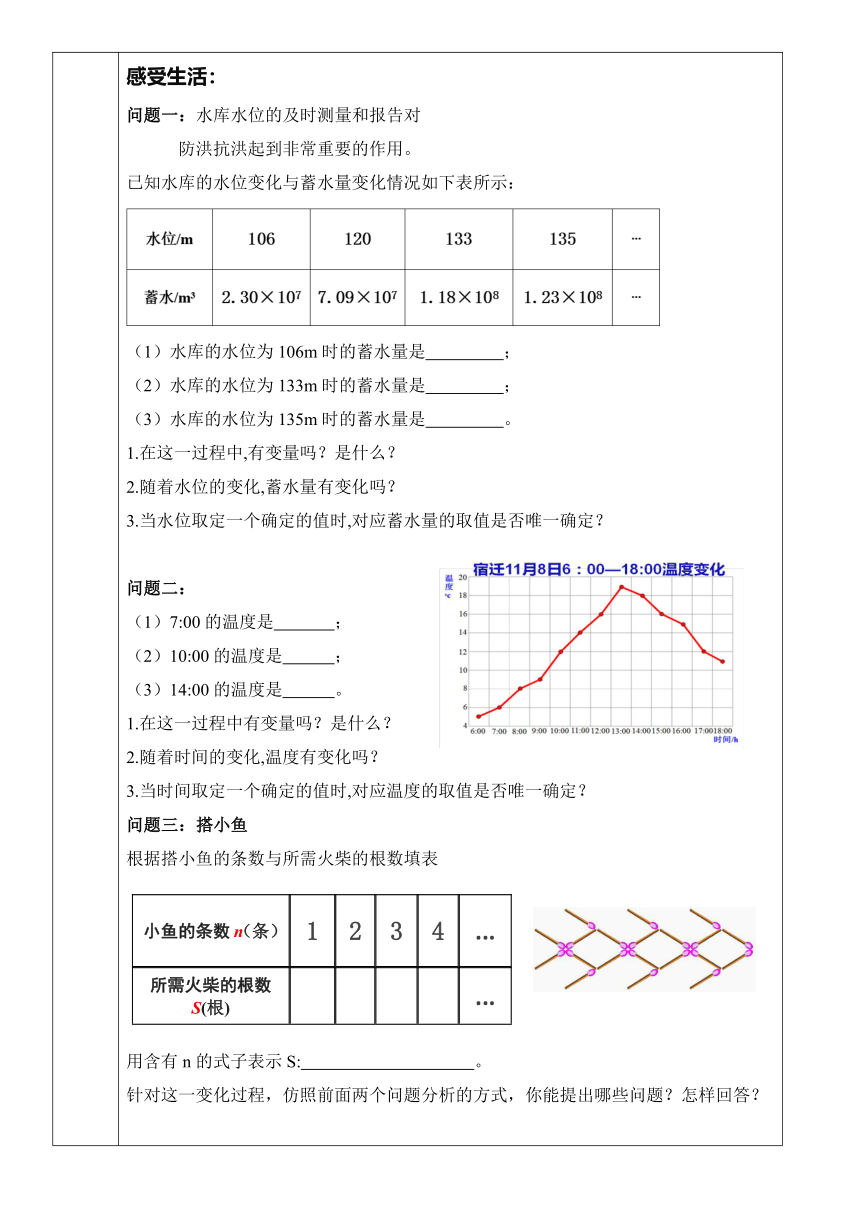
合作探究 新知探索: 列车从甲地驶往乙地,当汽车速度v以200千米/时匀速行驶,已经行驶路程为s千米,时间为t小时. 在这一运动过程中哪些量没有变化?哪些量是不断变化的 定义: 在某一变化过程中,数值保值不变的量叫做 ,可以取不同数值的量叫做 。 变式: 列车从相距s千米的甲地驶往乙地,当汽车以v千米/时的速度行驶时,t小时到达. 在这一运动过程中哪些量没有变化?哪些量是不断变化的 总结:常量和变量不是 而是 的,是针对某一特定变化过程而言的。 练习巩固: 1. 一斤苹果1.2元,买x斤这样的苹果y元,其中常量是____,变量是________。 2.小明为班级购买的某种钢笔单价6元/支,买m支钢笔,支付了n元钱,其中常量是 ,变量是 。 3. 长方形的长为a,宽为5,它的面积S,其中常量是____,变量是________。 你还能举出一些类似的实例吗? 感受生活: 问题一:水库水位的及时测量和报告对 防洪抗洪起到非常重要的作用。 已知水库的水位变化与蓄水量变化情况如下表所示: (1)水库的水位为106m时的蓄水量是 ; (2)水库的水位为133m时的蓄水量是 ; (3)水库的水位为135m时的蓄水量是 。 1.在这一过程中,有变量吗?是什么? 2.随着水位的变化,蓄水量有变化吗? 3.当水位取定一个确定的值时,对应蓄水量的取值是否唯一确定? (
宿迁未来十天最高气温预报
)问题二: (1)7:00的温度是 ; (2)10:00的温度是 ; (3)14:00的温度是 。 1.在这一过程中有变量吗?是什么? 2.随着时间的变化,温度有变化吗? 3.当时间取定一个确定的值时,对应温度的取值是否唯一确定? 问题三:搭小鱼 根据搭小鱼的条数与所需火柴的根数填表 小鱼的条数n(条)1234...所需火柴的根数S(根)...
用含有n的式子表示S: 。 针对这一变化过程,仿照前面两个问题分析的方式,你能提出哪些问题?怎样回答? 这些变化过程中,有什么共同的特点? 你还能举出一些类似的实例吗? 定义归纳: 一般地,在一个变化的过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么我们称:y是x的函数. 其中x是自变量
应用评价 练习巩固: 1.b是a的函数吗?为什么? 变式: b是a的函数吗?为什么? 2.用一根40cm的绳子围成一个长方形. (1)当长方形的宽为5cm时,长为 cm; (2)当长方形的宽为8cm时,长为 cm; (3)当长方形的宽为acm时,长为 cm; (4)长方形的长是宽的函数吗?为什么? 3.(1)根据图片上的信息完成表格; (2)弹簧长是砝码质量的函数吗?为什么? 砝码质量x/g0100200300弹簧长y/cm
4.按图示的运算程序,输入一个实数 x ,便可输 出一个相应的实数 y. y 是 x 的函数吗?为什么? 课堂小结: 1、本节课你学到了什么? 2、你还有什么疑问或想知道的吗?
板书设计 6.1函数 变化量 生活 方程 相等量 唯一确定 1.常量 变量 2.定义: 桔子 2.5元/斤 一般地,在一个变化的过程中有两个变量x和y, x斤 y元 如果对于x的每一个值,y都有唯一的值与它对应, 那么我们称:y是x的函数. 尺子 3元/套 其中x是自变量 x套 y元
学习目标 1.通过简单实例,了解常量与变量的意义; 2.通过实例,让学生多角度、多层面地认识和理解函数的意义,感受函数的多种表示形式; 3.能说出一些函数的实例,并能判断两个变量间的关系是否是函数关系。
重点难点 重点:函数概念的建立;判断两个变量间的关系是否是函数关系。 难点:函数概念中的常量、变量的理解及其对应关系探索。
学习过程
情景激活 情境导入: “变化”引领我们去探索新知识,这节课就让我们在变化过程中去感悟新的领域——函数。
合作探究 新知探索: 列车从甲地驶往乙地,当汽车速度v以200千米/时匀速行驶,已经行驶路程为s千米,时间为t小时. 在这一运动过程中哪些量没有变化?哪些量是不断变化的 定义: 在某一变化过程中,数值保值不变的量叫做 ,可以取不同数值的量叫做 。 变式: 列车从相距s千米的甲地驶往乙地,当汽车以v千米/时的速度行驶时,t小时到达. 在这一运动过程中哪些量没有变化?哪些量是不断变化的 总结:常量和变量不是 而是 的,是针对某一特定变化过程而言的。 练习巩固: 1. 一斤苹果1.2元,买x斤这样的苹果y元,其中常量是____,变量是________。 2.小明为班级购买的某种钢笔单价6元/支,买m支钢笔,支付了n元钱,其中常量是 ,变量是 。 3. 长方形的长为a,宽为5,它的面积S,其中常量是____,变量是________。 你还能举出一些类似的实例吗? 感受生活: 问题一:水库水位的及时测量和报告对 防洪抗洪起到非常重要的作用。 已知水库的水位变化与蓄水量变化情况如下表所示: (1)水库的水位为106m时的蓄水量是 ; (2)水库的水位为133m时的蓄水量是 ; (3)水库的水位为135m时的蓄水量是 。 1.在这一过程中,有变量吗?是什么? 2.随着水位的变化,蓄水量有变化吗? 3.当水位取定一个确定的值时,对应蓄水量的取值是否唯一确定? (
宿迁未来十天最高气温预报
)问题二: (1)7:00的温度是 ; (2)10:00的温度是 ; (3)14:00的温度是 。 1.在这一过程中有变量吗?是什么? 2.随着时间的变化,温度有变化吗? 3.当时间取定一个确定的值时,对应温度的取值是否唯一确定? 问题三:搭小鱼 根据搭小鱼的条数与所需火柴的根数填表 小鱼的条数n(条)1234...所需火柴的根数S(根)...
用含有n的式子表示S: 。 针对这一变化过程,仿照前面两个问题分析的方式,你能提出哪些问题?怎样回答? 这些变化过程中,有什么共同的特点? 你还能举出一些类似的实例吗? 定义归纳: 一般地,在一个变化的过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么我们称:y是x的函数. 其中x是自变量
应用评价 练习巩固: 1.b是a的函数吗?为什么? 变式: b是a的函数吗?为什么? 2.用一根40cm的绳子围成一个长方形. (1)当长方形的宽为5cm时,长为 cm; (2)当长方形的宽为8cm时,长为 cm; (3)当长方形的宽为acm时,长为 cm; (4)长方形的长是宽的函数吗?为什么? 3.(1)根据图片上的信息完成表格; (2)弹簧长是砝码质量的函数吗?为什么? 砝码质量x/g0100200300弹簧长y/cm
4.按图示的运算程序,输入一个实数 x ,便可输 出一个相应的实数 y. y 是 x 的函数吗?为什么? 课堂小结: 1、本节课你学到了什么? 2、你还有什么疑问或想知道的吗?
板书设计 6.1函数 变化量 生活 方程 相等量 唯一确定 1.常量 变量 2.定义: 桔子 2.5元/斤 一般地,在一个变化的过程中有两个变量x和y, x斤 y元 如果对于x的每一个值,y都有唯一的值与它对应, 那么我们称:y是x的函数. 尺子 3元/套 其中x是自变量 x套 y元
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
