22.2 二次函数与一元二次方程课件(共18张PPT)
文档属性
| 名称 | 22.2 二次函数与一元二次方程课件(共18张PPT) | 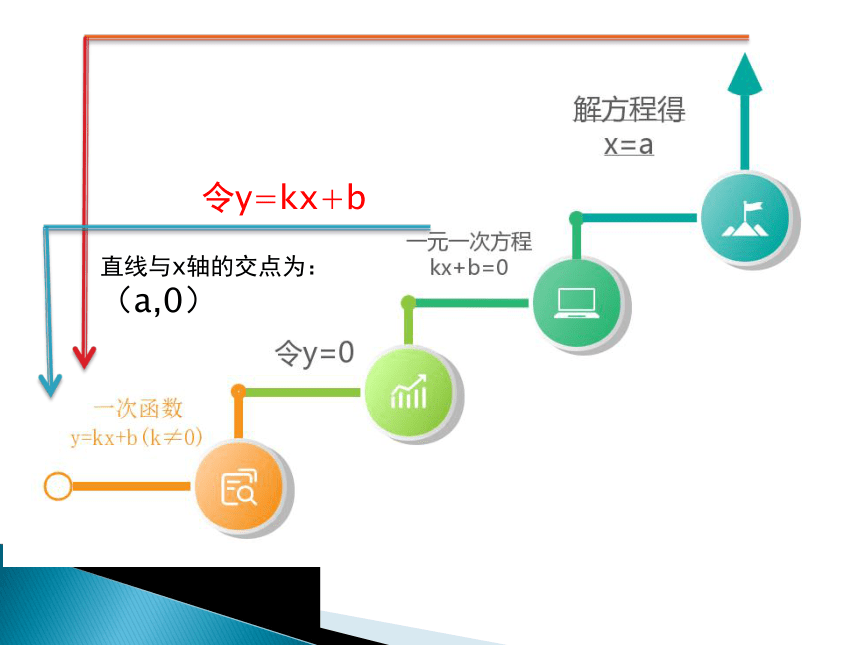 | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 21:40:44 | ||
图片预览




文档简介
(共18张PPT)
直线与x轴的交点为:
(a,0)
令y=kx+b
22.2二次函数与一元二次方程
问题
书P43页
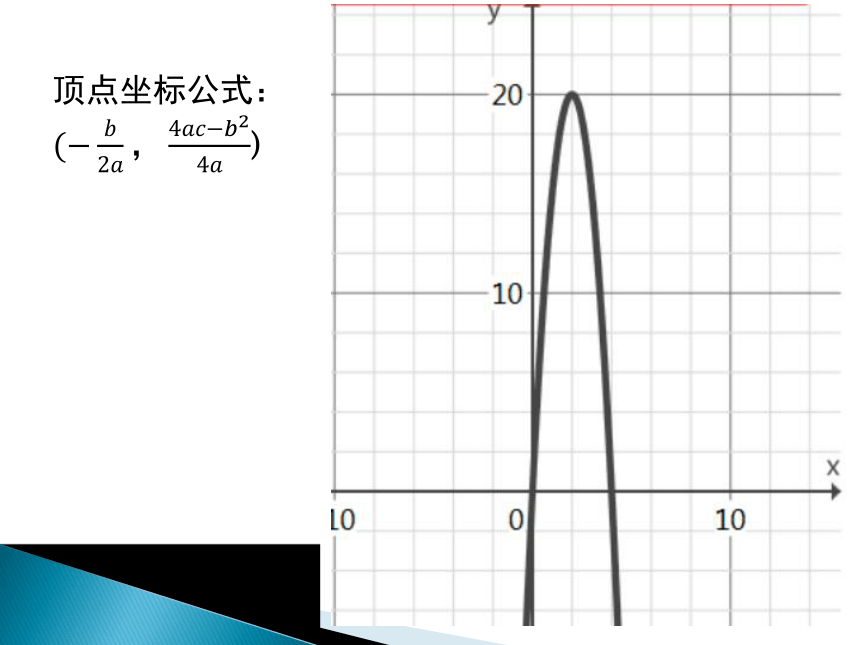
小球飞出的高度能否达到
(1)15m
(2)20m
(3)20.5m
用函数最值可同时解决3个问题。
)
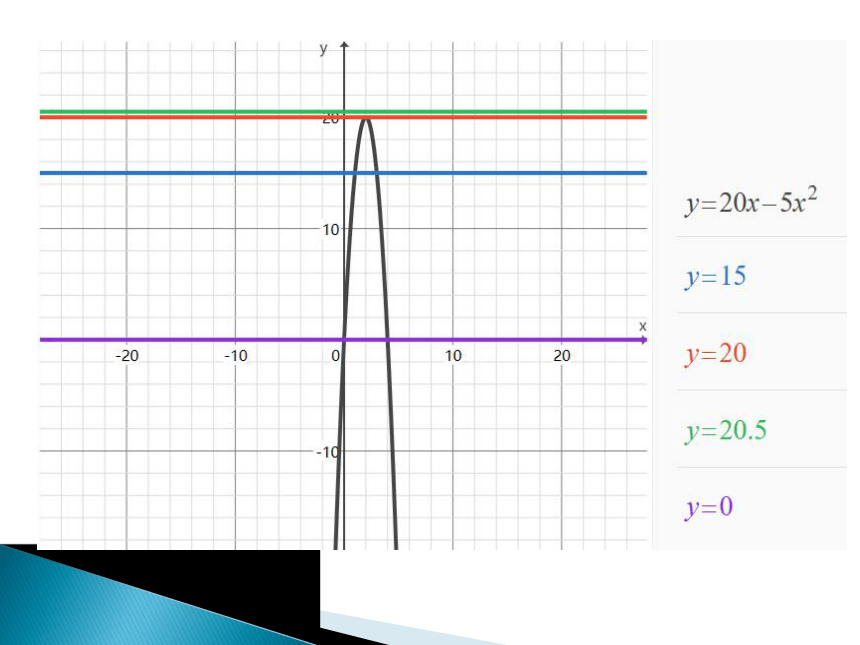
小球飞出的高度能否达到
(1)15m 如果能,什么时候达到?
(2)20m 如果能,什么时候达到?
(3)20.5m 如果能,什么时候达到?
用函数图象可解决。但可能不太准确。
特别地,我们研究:
当y=0时得方程,此时方程的解为二次函数y=0时对应的自变量x的值,在图象上对应抛物线与x轴交点的横坐标。
令,此时二次函数y=0时对应的自变量x的值为方程的解,图象上抛物线与x轴交点的横坐标对应着方程的解。
用法:
已知二次函数,求抛物线与x轴的交点横坐标;
已知方程,利用图象抛物线与x轴的交点横坐标求方程的解。
例如:
与x轴的交点坐标。
例如:
问题:
是不是所有抛物线与x轴都有交点呢?
是不是所有一元二次方程都有解呢?
二次函数解析式 图象 与x轴的交点个数 方程解的情况
+x-2 +x-2=0
x+9
x+9=0
x+1
x+1=0
两个不同交点
△>0,方程有两个不相等的实数根
只有一个交点
△=0,方程有两个相等的实数根
没有交点
△<0,方程没有实数根。
二次函数解析式 图象 与x轴的交点个数 方程解的情况
+bx+c 两个不同交点 交点坐标为: (,0)(,0) +bx+c=0
△>0,方程有两个不相等的实数根
,
x+c 只有一个交点 交点坐标为: (,0) ax+c=0
△=0,方程有两个相等的实数根
=
x+c 没有交点
x+c=0
△<0,方程没有实数根。
用法:
由抛物线与x轴的交点坐标个数可判断一元二次方程根的个数;反之,由差别式△的情况,要得根的情况,从而判定抛物线与x轴的交点个数。
例子:利用函数图象求方程的实数根。(结果保留小数点后一位)
方法二:夹逼法
方法一:直接估计
小结:
1、知识:已知二次函数的函数y值,可以代入函数解析式转化为一元二次方程来求相应的自变量x的值,对应着函数图象上的两点的坐标。
反之,已知一元二次方程,可借助二次函数的图象来求方程的解。方程的解是二次函数图象与x轴的交点横坐标。
2、数学思想方法:转化思想,特殊到一般的思想;数形结合的思想。
谢 谢
直线与x轴的交点为:
(a,0)
令y=kx+b
22.2二次函数与一元二次方程
问题
书P43页
小球飞出的高度能否达到
(1)15m
(2)20m
(3)20.5m
用函数最值可同时解决3个问题。
)
小球飞出的高度能否达到
(1)15m 如果能,什么时候达到?
(2)20m 如果能,什么时候达到?
(3)20.5m 如果能,什么时候达到?
用函数图象可解决。但可能不太准确。
特别地,我们研究:
当y=0时得方程,此时方程的解为二次函数y=0时对应的自变量x的值,在图象上对应抛物线与x轴交点的横坐标。
令,此时二次函数y=0时对应的自变量x的值为方程的解,图象上抛物线与x轴交点的横坐标对应着方程的解。
用法:
已知二次函数,求抛物线与x轴的交点横坐标;
已知方程,利用图象抛物线与x轴的交点横坐标求方程的解。
例如:
与x轴的交点坐标。
例如:
问题:
是不是所有抛物线与x轴都有交点呢?
是不是所有一元二次方程都有解呢?
二次函数解析式 图象 与x轴的交点个数 方程解的情况
+x-2 +x-2=0
x+9
x+9=0
x+1
x+1=0
两个不同交点
△>0,方程有两个不相等的实数根
只有一个交点
△=0,方程有两个相等的实数根
没有交点
△<0,方程没有实数根。
二次函数解析式 图象 与x轴的交点个数 方程解的情况
+bx+c 两个不同交点 交点坐标为: (,0)(,0) +bx+c=0
△>0,方程有两个不相等的实数根
,
x+c 只有一个交点 交点坐标为: (,0) ax+c=0
△=0,方程有两个相等的实数根
=
x+c 没有交点
x+c=0
△<0,方程没有实数根。
用法:
由抛物线与x轴的交点坐标个数可判断一元二次方程根的个数;反之,由差别式△的情况,要得根的情况,从而判定抛物线与x轴的交点个数。
例子:利用函数图象求方程的实数根。(结果保留小数点后一位)
方法二:夹逼法
方法一:直接估计
小结:
1、知识:已知二次函数的函数y值,可以代入函数解析式转化为一元二次方程来求相应的自变量x的值,对应着函数图象上的两点的坐标。
反之,已知一元二次方程,可借助二次函数的图象来求方程的解。方程的解是二次函数图象与x轴的交点横坐标。
2、数学思想方法:转化思想,特殊到一般的思想;数形结合的思想。
谢 谢
同课章节目录
