2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册 2.5.1 直线与圆的位置关系 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册 2.5.1 直线与圆的位置关系 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 391.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 21:14:49 | ||
图片预览






文档简介
(共27张PPT)
第二章 直线和圆的方程
2.5.1直线与圆的位置关系
一、创设情境 引入新课
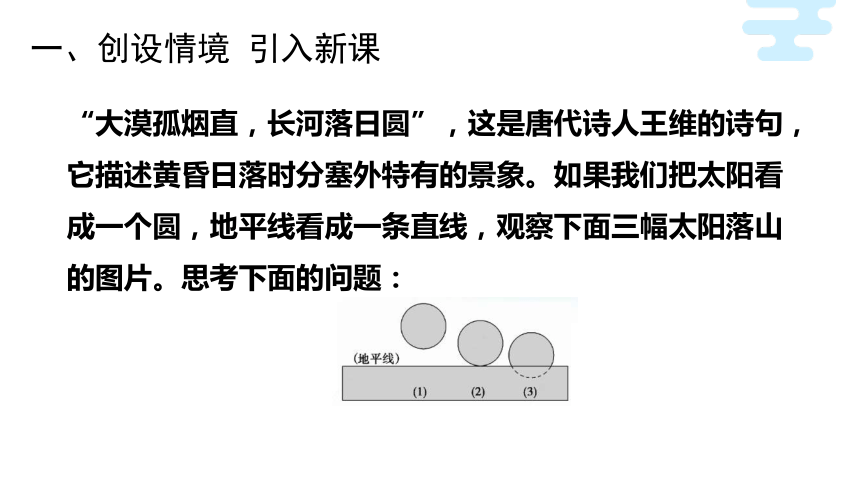
“大漠孤烟直,长河落日圆”,这是唐代诗人王维的诗句, 它描述黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,观察下面三幅太阳落山的图片。思考下面的问题:
二、探究本质得新知
探究一:直线与圆的位置关系
问题1:图片中,地平线与太阳的位置关系怎样?
提示:①相离;②相切;③相交.
二、探究本质得新知
问题2:如何判断直线与圆的位置关系?
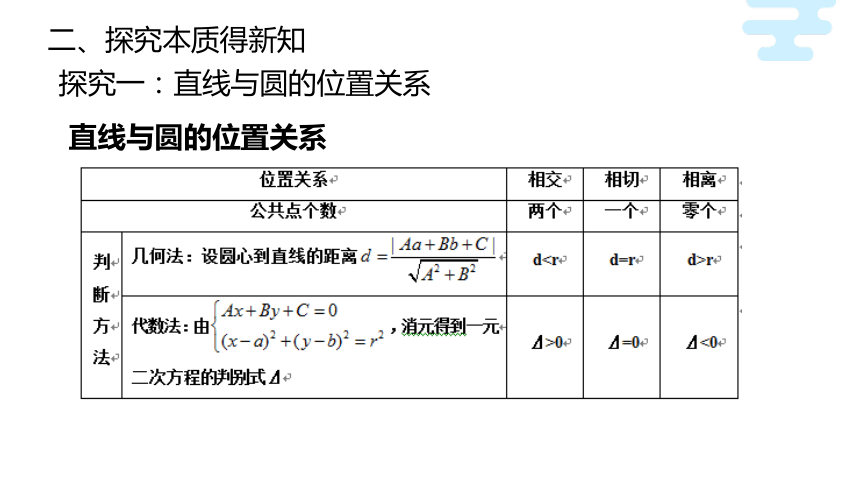
提示:(1)通过直线和圆的方程组成的方程组解的情况判断直线与圆的位置关系
(2)可利用圆心到直线的距离d与半径r的大小关系.
探究一:直线与圆的位置关系
二、探究本质得新知
直线与圆的位置关系
探究一:直线与圆的位置关系
二、探究本质得新知
探究二:直线与圆的相切与相交问题
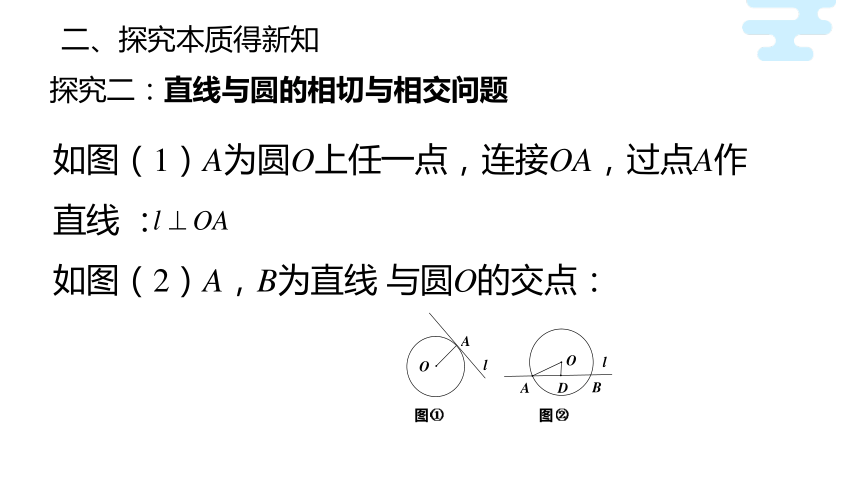
如图(1)A为圆O上任一点,连接OA,过点A作直线 :
如图(2)A,B为直线 与圆O的交点:
二、探究本质得新知
探究二:直线与圆的相切与相交问题
问题1:图①中,圆心O到直线l的距离d和圆的半径r
有什么关系?
提示:相等
问题2:直线l和圆O的位置有什么关系?依据是什么?
提示:相切,依据是d=r.
二、探究本质得新知
探究二:直线与圆的相切与相交问题
问题3:图②中,若弦AB的长记为L,结合图形L,d,r之间有什么关系?
提示:
问题4:直线l和圆O相交于A,B两点,当直线l满足什么条件时,截得的弦长|AB|最长?
提示:当直线l过圆O的圆心时,截得的弦|AB|最长为2r
三、举例应用,掌握定义
例1:已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,圆与直线:
①有两个公共点;
②只有一个公共点;
③没有公共点.
三、举例应用,掌握定义
【解析】方法一:将直线mx-y-m-1=0代入圆的方程化简整理得,
(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
则Δ=4m(3m+4).
当Δ>0,即m>0或m<- 时,直线与圆相交,即直线与圆有两个公共点;
当Δ=0,即m=0或m=- 时,直线与圆相切,即直线与圆只有一个公共点;
当Δ<0,即 -三、举例应用,掌握定义
方法二:已知圆的方程可化为(x-2)2+(y-1)2=4,
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx-y-m-1=0的距离
d=
当d<2,即m>0或m<- 时,直线与圆相交,即直线与圆有两个公共点;
当d=2,即m=0或m=- 时,直线与圆相切,即直线与圆只有一个公共点;
当d>2,即 -三、举例应用,掌握定义
例2.过点P(1,1) 作圆 : 的切线方程为 .
【解析】圆 C: ,配方得:
圆心C(0,4) ,半径 r=
①当直线l 的斜率不存在时,l :x=1,此时l不与圆相切.
②若直线 l的斜率存在,设 l:y-1=k(x-1) ,
由 得 k=7或-1,所以直线方程为 7x-y-6=0或x+y-2=0 .
答案:为 7x-y-6=0 或 x+y-2=0
三、举例应用,掌握定义
三、举例应用,掌握定义
三、举例应用,掌握定义
三、举例应用,掌握定义
例4:(1)一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过 ( )
A.1.4米 B.3.5米 C.3.6米 D.2米
三、举例应用,掌握定义
【解析】(1)选B.建立如图所示的平面直角坐标系.如图设蓬顶距地面高度为h,则A(0.8,h-3.6)所在圆的方程为: x2+(y+3.6)2=3.62,把A(0.8,h-3.6)代入得0.82+h2=3.62.所以h=4 ≈3.5(米).
三、举例应用,掌握定义
(2)台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A地正东40 km处,则城市B处于危险区内的时间为( )
A.0.5 h B.1 h C.1.5 h D.2 h
三、举例应用,掌握定义
(2)选B.如图,以A地为原点,AB所在直线为x轴,建立平面直角坐标系,则以B(40,0)为圆心,30为半径的圆内MN之间(含端点)为危险区,取MN的中点E,连接BE,BN,BM,则BE⊥MN,BN=BM,△ABE为等腰直角三角形,因为AB=40,所以BE=20 km,在Rt△BEN中,NE= =10,则|MN|=20,所以时间为1 h.
四、学生练习,加深理解
1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是 ( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
四、学生练习,加深理解
【解析】选D.圆心(1,-1)到直线3x+4y+12=0的距离d= ,0四、学生练习,加深理解
2.圆心为(3,0)且与直线x+ y=0相切的圆的方程为()
A.(x- )2+y2=1 B.(x-3)2+y2=3
C.(x- )2+y2=3 D.(x-3)2+y2=9
【解析】选B. 由题意知所求圆的半径r= ,故所求圆的方程为(x-3)2+y2=3.
四、学生练习,加深理解
3. 已知直线 都是正数)与圆 相切,则以a,b,c 为三边长的三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
【解析】选B.因为直线与圆相切,所以圆心到直线的距离d= =1,得a2+b2=c2,所以以a,b,c 为三边长的三角形是直角三角形.
四、学生练习,加深理解
4.若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为________.
【解析】设切线斜率为k,则由已知得: k·kOP=-1.
所以k=- .∴切线方程为x+2y-5=0.
答案:x+2y-5=0
四、学生练习,加深理解
5.求直线l:3x+y-6=0被圆C: x2+y2-2y-4=0截得的弦长.
【解析】圆C: x2+y2-2y-4=0可化为x2+(y-1)2=5.其圆心坐标为C(0,1),半径r= ,点C(0,1)到直线l的距离为d= ,所以半弦长
所以弦长|AB|=
1.知识方面:(1)直线与圆的位置关系的判断方法。
(2)能够解决直线与圆的相切、相交问题
2.能力方面:能够用所学知识解决一些实际问题。
3.思想方面:体升了数学运算素养和逻辑推理的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P98 2,3,4题
第二章 直线和圆的方程
2.5.1直线与圆的位置关系
一、创设情境 引入新课
“大漠孤烟直,长河落日圆”,这是唐代诗人王维的诗句, 它描述黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,观察下面三幅太阳落山的图片。思考下面的问题:
二、探究本质得新知
探究一:直线与圆的位置关系
问题1:图片中,地平线与太阳的位置关系怎样?
提示:①相离;②相切;③相交.
二、探究本质得新知
问题2:如何判断直线与圆的位置关系?
提示:(1)通过直线和圆的方程组成的方程组解的情况判断直线与圆的位置关系
(2)可利用圆心到直线的距离d与半径r的大小关系.
探究一:直线与圆的位置关系
二、探究本质得新知
直线与圆的位置关系
探究一:直线与圆的位置关系
二、探究本质得新知
探究二:直线与圆的相切与相交问题
如图(1)A为圆O上任一点,连接OA,过点A作直线 :
如图(2)A,B为直线 与圆O的交点:
二、探究本质得新知
探究二:直线与圆的相切与相交问题
问题1:图①中,圆心O到直线l的距离d和圆的半径r
有什么关系?
提示:相等
问题2:直线l和圆O的位置有什么关系?依据是什么?
提示:相切,依据是d=r.
二、探究本质得新知
探究二:直线与圆的相切与相交问题
问题3:图②中,若弦AB的长记为L,结合图形L,d,r之间有什么关系?
提示:
问题4:直线l和圆O相交于A,B两点,当直线l满足什么条件时,截得的弦长|AB|最长?
提示:当直线l过圆O的圆心时,截得的弦|AB|最长为2r
三、举例应用,掌握定义
例1:已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,圆与直线:
①有两个公共点;
②只有一个公共点;
③没有公共点.
三、举例应用,掌握定义
【解析】方法一:将直线mx-y-m-1=0代入圆的方程化简整理得,
(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
则Δ=4m(3m+4).
当Δ>0,即m>0或m<- 时,直线与圆相交,即直线与圆有两个公共点;
当Δ=0,即m=0或m=- 时,直线与圆相切,即直线与圆只有一个公共点;
当Δ<0,即 -
方法二:已知圆的方程可化为(x-2)2+(y-1)2=4,
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx-y-m-1=0的距离
d=
当d<2,即m>0或m<- 时,直线与圆相交,即直线与圆有两个公共点;
当d=2,即m=0或m=- 时,直线与圆相切,即直线与圆只有一个公共点;
当d>2,即 -
例2.过点P(1,1) 作圆 : 的切线方程为 .
【解析】圆 C: ,配方得:
圆心C(0,4) ,半径 r=
①当直线l 的斜率不存在时,l :x=1,此时l不与圆相切.
②若直线 l的斜率存在,设 l:y-1=k(x-1) ,
由 得 k=7或-1,所以直线方程为 7x-y-6=0或x+y-2=0 .
答案:为 7x-y-6=0 或 x+y-2=0
三、举例应用,掌握定义
三、举例应用,掌握定义
三、举例应用,掌握定义
三、举例应用,掌握定义
例4:(1)一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过 ( )
A.1.4米 B.3.5米 C.3.6米 D.2米
三、举例应用,掌握定义
【解析】(1)选B.建立如图所示的平面直角坐标系.如图设蓬顶距地面高度为h,则A(0.8,h-3.6)所在圆的方程为: x2+(y+3.6)2=3.62,把A(0.8,h-3.6)代入得0.82+h2=3.62.所以h=4 ≈3.5(米).
三、举例应用,掌握定义
(2)台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A地正东40 km处,则城市B处于危险区内的时间为( )
A.0.5 h B.1 h C.1.5 h D.2 h
三、举例应用,掌握定义
(2)选B.如图,以A地为原点,AB所在直线为x轴,建立平面直角坐标系,则以B(40,0)为圆心,30为半径的圆内MN之间(含端点)为危险区,取MN的中点E,连接BE,BN,BM,则BE⊥MN,BN=BM,△ABE为等腰直角三角形,因为AB=40,所以BE=20 km,在Rt△BEN中,NE= =10,则|MN|=20,所以时间为1 h.
四、学生练习,加深理解
1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是 ( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
四、学生练习,加深理解
【解析】选D.圆心(1,-1)到直线3x+4y+12=0的距离d= ,0
2.圆心为(3,0)且与直线x+ y=0相切的圆的方程为()
A.(x- )2+y2=1 B.(x-3)2+y2=3
C.(x- )2+y2=3 D.(x-3)2+y2=9
【解析】选B. 由题意知所求圆的半径r= ,故所求圆的方程为(x-3)2+y2=3.
四、学生练习,加深理解
3. 已知直线 都是正数)与圆 相切,则以a,b,c 为三边长的三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
【解析】选B.因为直线与圆相切,所以圆心到直线的距离d= =1,得a2+b2=c2,所以以a,b,c 为三边长的三角形是直角三角形.
四、学生练习,加深理解
4.若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为________.
【解析】设切线斜率为k,则由已知得: k·kOP=-1.
所以k=- .∴切线方程为x+2y-5=0.
答案:x+2y-5=0
四、学生练习,加深理解
5.求直线l:3x+y-6=0被圆C: x2+y2-2y-4=0截得的弦长.
【解析】圆C: x2+y2-2y-4=0可化为x2+(y-1)2=5.其圆心坐标为C(0,1),半径r= ,点C(0,1)到直线l的距离为d= ,所以半弦长
所以弦长|AB|=
1.知识方面:(1)直线与圆的位置关系的判断方法。
(2)能够解决直线与圆的相切、相交问题
2.能力方面:能够用所学知识解决一些实际问题。
3.思想方面:体升了数学运算素养和逻辑推理的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P98 2,3,4题
