分式复习学案(无答案)
图片预览
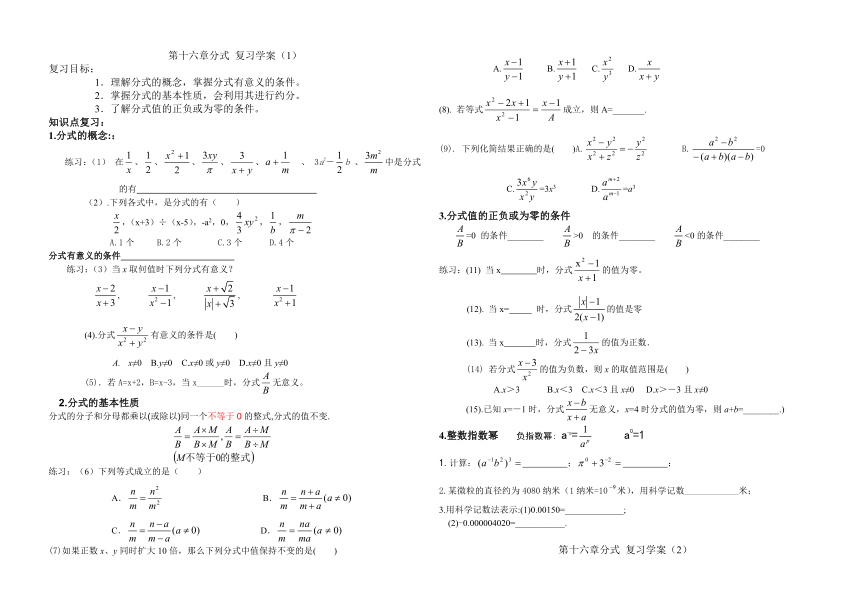
文档简介
第十六章分式 复习学案(1)
复习目标:
理解分式的概念,掌握分式有意义的条件。
掌握分式的基本性质,会利用其进行约分。
了解分式值的正负或为零的条件。
知识点复习:
1.分式的概念::
练习:(1) 在、、、、、 、 3a2-b 、中是分式的有
(2).下列各式中,是分式的有( )
,(x+3)÷(x-5),-a2,0,,,
A.1个 B.2个 C.3个 D.4个
分式有意义的条件
练习:(3)当x取何值时下列分式有意义?
, , ,
(4).分式有意义的条件是( )
x≠0 B.y≠0 C.x≠0或y≠0 D.x≠0且y≠0
(5).若A=x+2,B=x-3,当x______时,分式无意义。
2.分式的基本性质
分式的分子和分母都乘以(或除以)同一个不等于0的整式,分式的值不变.
练习:(6)下列等式成立的是( )
A. B.
C. D.
(7)如果正数x、y同时扩大10倍,那么下列分式中值保持不变的是( )
A. B. C. D.
(8). 若等式成立,则A=_______.
(9). 下列化简结果正确的是( )A. B.=0
C.=3x3 D.=a3
3.分式值的正负或为零的条件
=0 的条件________ >0 的条件________ <0的条件________
练习:(11) 当x 时,分式的值为零。
(12). 当x= 时,分式的值是零
(13). 当x 时,分式的值为正数.
(14) 若分式的值为负数,则x的取值范围是( )
A.x>3 B.x<3 C.x<3且x≠0 D.x>-3且x≠0
(15).已知x=-1时,分式无意义,x=4时分式的值为零,则a+b=________.)
4.整数指数幂 负指数幂: a-p= a0=1
1.计算: ; ;
2.某微粒的直径约为4080纳米(1纳米=10米),用科学记数____________米;
3.用科学记数法表示:(1)0.00150=_____________;
(2)-0.000004020=___________.
第十六章分式 复习学案(2)
1.分式乘法:
练习:(1).= (2). =
2. 分式除法:
练习:(3). = (4). =
(5). =
3.分式通分:
练习:(6).的最简公分母是 。
(7). 通分
4.分式加减:
练习:计算(8) (9).
(10). (11)
5.化简,求值。
1.先化简,再求值:,其中x=2
2. 已知-=5,则的值是 .
6.解分式方程
练习:1. 2.
7.分式方程无解的条件
1. 若方程有增根,则m的值是…………( )
2.若无解,则m的值是( )
8.方程思想的运用
1. 若关于x的方程的解是x=2,则a= ;
2.已知关于x的方程的解为负值,求m的取值范围。
9.分式方程应用题
(1)A、B两地的距离是80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度。
(2)为加快西部大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程。如果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则刚好如期完成。问原来规定修好这条公路需多长时间?
(3)某工人原计划在规定时间内恰好加工1500个零件,改进了工具和操作方法后,工作效率提高为原来的2倍,因此加工1500个零件时,比原计划提前了五小时,问原计划每小时加工多少个零件?
复习目标:
理解分式的概念,掌握分式有意义的条件。
掌握分式的基本性质,会利用其进行约分。
了解分式值的正负或为零的条件。
知识点复习:
1.分式的概念::
练习:(1) 在、、、、、 、 3a2-b 、中是分式的有
(2).下列各式中,是分式的有( )
,(x+3)÷(x-5),-a2,0,,,
A.1个 B.2个 C.3个 D.4个
分式有意义的条件
练习:(3)当x取何值时下列分式有意义?
, , ,
(4).分式有意义的条件是( )
x≠0 B.y≠0 C.x≠0或y≠0 D.x≠0且y≠0
(5).若A=x+2,B=x-3,当x______时,分式无意义。
2.分式的基本性质
分式的分子和分母都乘以(或除以)同一个不等于0的整式,分式的值不变.
练习:(6)下列等式成立的是( )
A. B.
C. D.
(7)如果正数x、y同时扩大10倍,那么下列分式中值保持不变的是( )
A. B. C. D.
(8). 若等式成立,则A=_______.
(9). 下列化简结果正确的是( )A. B.=0
C.=3x3 D.=a3
3.分式值的正负或为零的条件
=0 的条件________ >0 的条件________ <0的条件________
练习:(11) 当x 时,分式的值为零。
(12). 当x= 时,分式的值是零
(13). 当x 时,分式的值为正数.
(14) 若分式的值为负数,则x的取值范围是( )
A.x>3 B.x<3 C.x<3且x≠0 D.x>-3且x≠0
(15).已知x=-1时,分式无意义,x=4时分式的值为零,则a+b=________.)
4.整数指数幂 负指数幂: a-p= a0=1
1.计算: ; ;
2.某微粒的直径约为4080纳米(1纳米=10米),用科学记数____________米;
3.用科学记数法表示:(1)0.00150=_____________;
(2)-0.000004020=___________.
第十六章分式 复习学案(2)
1.分式乘法:
练习:(1).= (2). =
2. 分式除法:
练习:(3). = (4). =
(5). =
3.分式通分:
练习:(6).的最简公分母是 。
(7). 通分
4.分式加减:
练习:计算(8) (9).
(10). (11)
5.化简,求值。
1.先化简,再求值:,其中x=2
2. 已知-=5,则的值是 .
6.解分式方程
练习:1. 2.
7.分式方程无解的条件
1. 若方程有增根,则m的值是…………( )
2.若无解,则m的值是( )
8.方程思想的运用
1. 若关于x的方程的解是x=2,则a= ;
2.已知关于x的方程的解为负值,求m的取值范围。
9.分式方程应用题
(1)A、B两地的距离是80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度。
(2)为加快西部大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程。如果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则刚好如期完成。问原来规定修好这条公路需多长时间?
(3)某工人原计划在规定时间内恰好加工1500个零件,改进了工具和操作方法后,工作效率提高为原来的2倍,因此加工1500个零件时,比原计划提前了五小时,问原计划每小时加工多少个零件?
