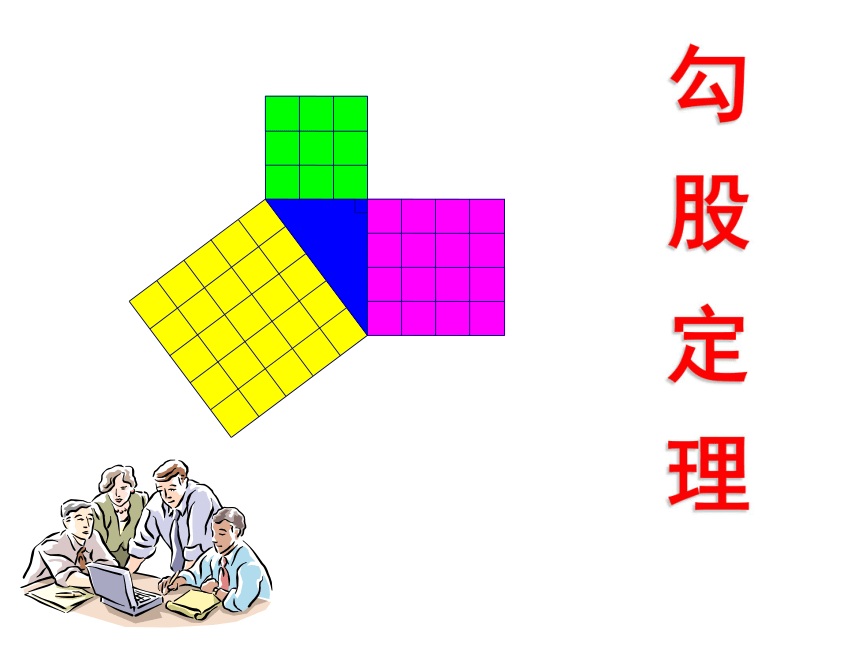
勾股定理
图片预览



文档简介
(共28张PPT)
勾 股 定 理
邮票赏析
这是1955年希腊为了纪念一位数学家而发行的一枚邮票。
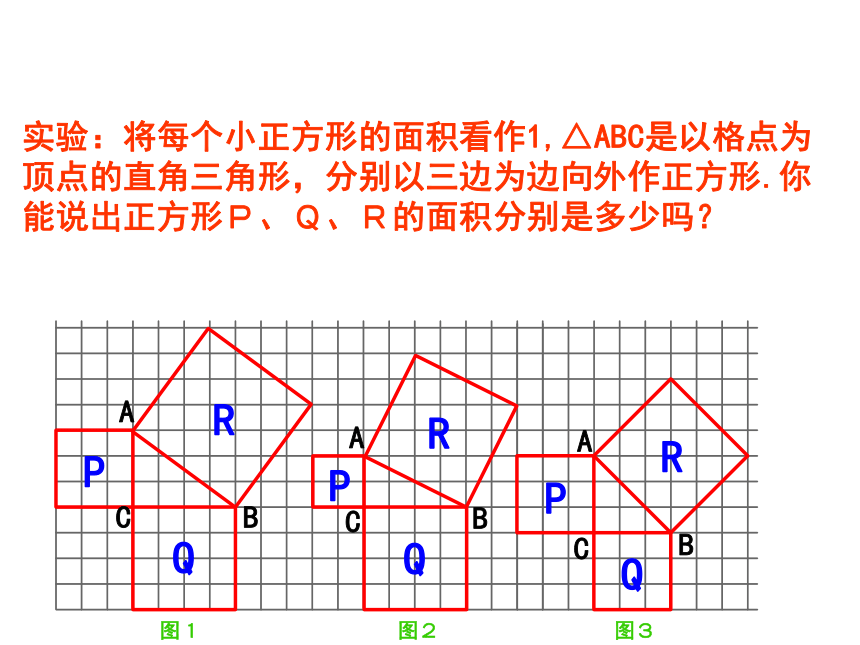
观察这三个正方形图案中小方格的个数,你有什么发现?
实验:将每个小正方形的面积看作1,△ABC是以格点为顶点的直角三角形,分别以三边为边向外作正方形.你能说出正方形P、Q、R的面积分别是多少吗?
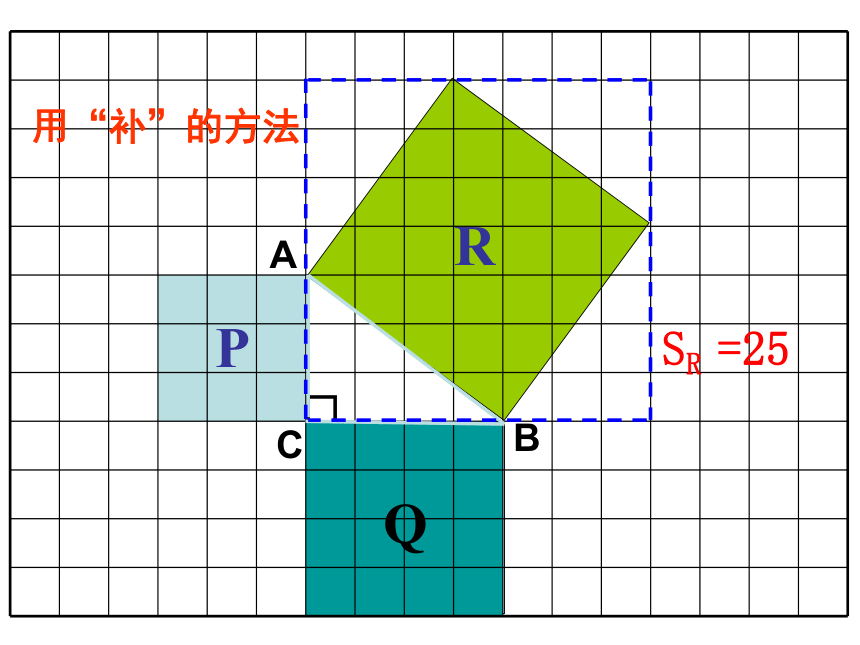
用“补”的方法
SR =25
P
Q
R
A
B
C
R
用“割”的方法
P
Q
SR =25
A
B
C
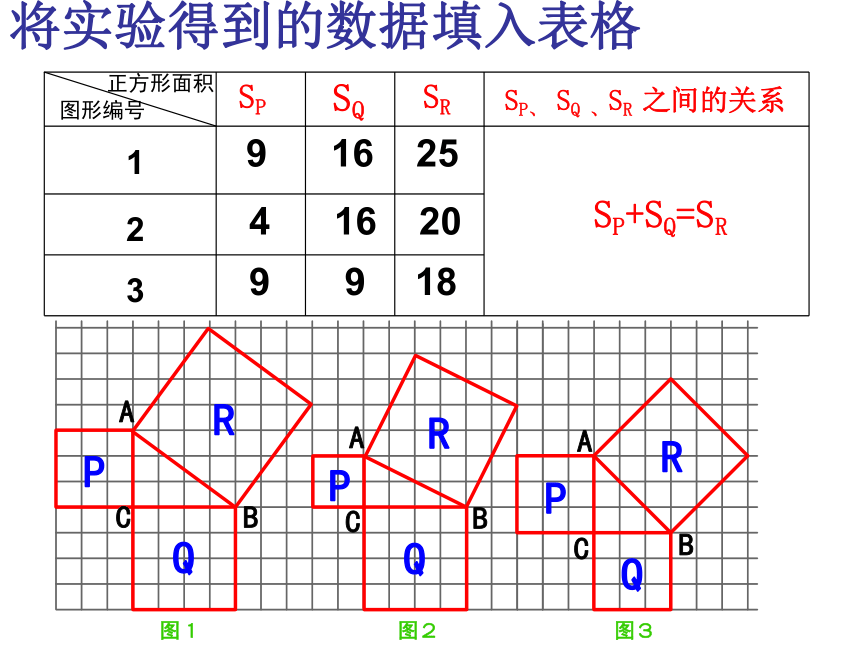
将实验得到的数据填入表格
正方形面积
图形编号
SP、 SQ 、SR 之间的关系
3
2
1
9 16 25
9 9 18
4 16 20
SR
SQ
SP
SP+SQ=SR
两直角边a、b与斜边c 之间又有什么关系?
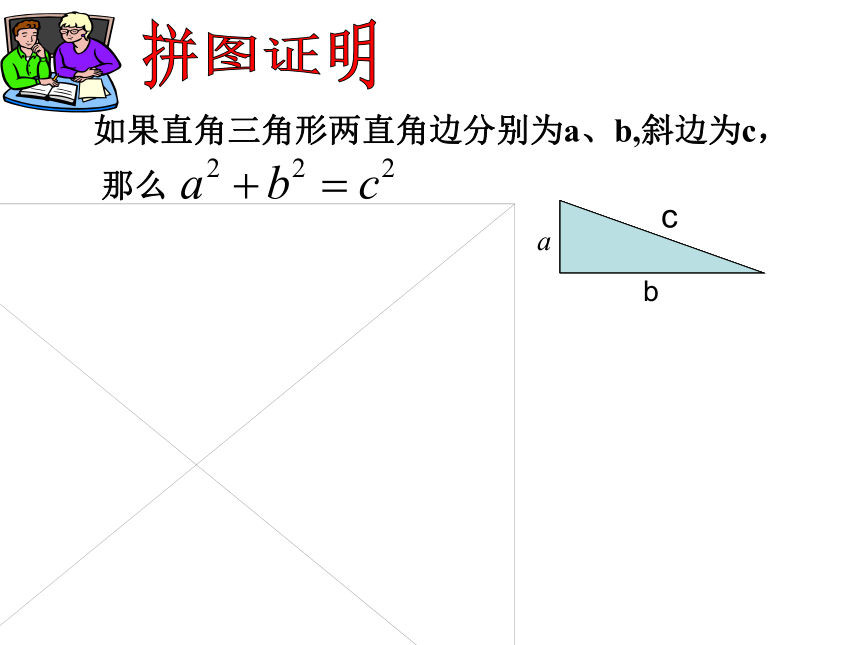
a2+b2=c2
P
R
A
B
C
c
b
a
Q
SP+SQ=SR
c
a
b
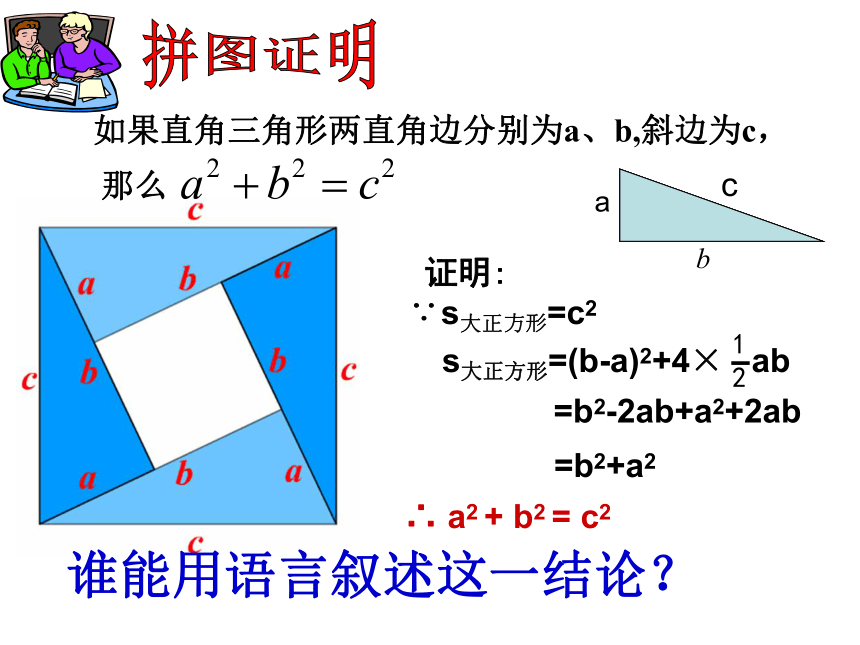
如果直角三角形两直角边分别为a、b,斜边为c,
那么
c
b
a
证明:
∵s大正方形=c2
∴ a2 + b2 = c2
如果直角三角形两直角边分别为a、b,斜边为c,
那么
s大正方形=(b-a)2+4× ab
1
2
谁能用语言叙述这一结论?
=b2+a2
=b2-2ab+a2+2ab
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
定理:经过证明被确认为正确的命题叫做定理。
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
a
b
c
公式变形:a2=c2-b2 b2=c2-a2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾 股 世 界
勾股定理的发现,充分反映了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.正因为此这个图案被选为2002年在北京召开的国际数学家大会的会徽。
1.求下列直角三角形中未知边的长:
已知直角三角形的任意两边, 可利用勾股定理求出第三边.
方法小结:
8
x
17
8
10
x
12
5
x
x=15
x=6
x=13
①
②
③
2、已知:△ABC是直角三角形,AB=4,AC=3,
则BC为 .
5
4
3
A
C
B
4
3
C
A
B
或
y=0
1、如图,受台风的影响,一棵树在离地面2米处断裂,树的顶部落在离树跟底部1.5米处,这棵树折断前有多高?
应用知识回归生活
2米
1.5米
A
B
C
2
1.5
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少
x+1
B
C
A
H
1
2
┓
x
x2+22=(x+1)2
盛开的水莲
方法小结:
在直角三角形中,如果已知一边及另两边之间的关系,也可以利用勾股定理求出另两边的长.
一、判断题:
1.在直角三角形ABC中,a2+b2=c2. ( )
2.直角三角形两直角边长都为1, 那么
斜边为2。 ( )
3.三角形ABC中,如果较短的二条边
分别为3和4,那么较长的边是5。 ( )
×
×
×
注意:c可不一定是斜边喔!
定理的结论应该是两直角边的平方和等于斜边的平方!
可要看清楚是不是直角三角形啊!!!
1.在△ABC中,∠C=90°,
(1)若 a=5,b=12,则c=_____;
(2)若 a=15,c=25,则b=_____;
(3)若a:b=3:4,c=10,
则a=___,b=___.
二、计算题
13
20
6
8
2. 如图:∠C=∠ABD=90°,AC=4,BC=3,
BD=12,则AD的长等于 .
3.已知:Rt⊿ABC中, ∠C=90°,
∠B=30°,AC=3cm,求BC的长。
30°
回味无穷
知识象一艘船
让它载着我们
驶向理想的
……
敬请指导
再见
4.等腰三角形的腰长为10,底边上的
高为6,则底边的长为 .
回味无穷
知识象一艘船
让它载着我们
驶向理想的
……
敬请指导
再见
勾 股 定 理
邮票赏析
这是1955年希腊为了纪念一位数学家而发行的一枚邮票。
观察这三个正方形图案中小方格的个数,你有什么发现?
实验:将每个小正方形的面积看作1,△ABC是以格点为顶点的直角三角形,分别以三边为边向外作正方形.你能说出正方形P、Q、R的面积分别是多少吗?
用“补”的方法
SR =25
P
Q
R
A
B
C
R
用“割”的方法
P
Q
SR =25
A
B
C
将实验得到的数据填入表格
正方形面积
图形编号
SP、 SQ 、SR 之间的关系
3
2
1
9 16 25
9 9 18
4 16 20
SR
SQ
SP
SP+SQ=SR
两直角边a、b与斜边c 之间又有什么关系?
a2+b2=c2
P
R
A
B
C
c
b
a
Q
SP+SQ=SR
c
a
b
如果直角三角形两直角边分别为a、b,斜边为c,
那么
c
b
a
证明:
∵s大正方形=c2
∴ a2 + b2 = c2
如果直角三角形两直角边分别为a、b,斜边为c,
那么
s大正方形=(b-a)2+4× ab
1
2
谁能用语言叙述这一结论?
=b2+a2
=b2-2ab+a2+2ab
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
定理:经过证明被确认为正确的命题叫做定理。
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
a
b
c
公式变形:a2=c2-b2 b2=c2-a2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾 股 世 界
勾股定理的发现,充分反映了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.正因为此这个图案被选为2002年在北京召开的国际数学家大会的会徽。
1.求下列直角三角形中未知边的长:
已知直角三角形的任意两边, 可利用勾股定理求出第三边.
方法小结:
8
x
17
8
10
x
12
5
x
x=15
x=6
x=13
①
②
③
2、已知:△ABC是直角三角形,AB=4,AC=3,
则BC为 .
5
4
3
A
C
B
4
3
C
A
B
或
y=0
1、如图,受台风的影响,一棵树在离地面2米处断裂,树的顶部落在离树跟底部1.5米处,这棵树折断前有多高?
应用知识回归生活
2米
1.5米
A
B
C
2
1.5
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少
x+1
B
C
A
H
1
2
┓
x
x2+22=(x+1)2
盛开的水莲
方法小结:
在直角三角形中,如果已知一边及另两边之间的关系,也可以利用勾股定理求出另两边的长.
一、判断题:
1.在直角三角形ABC中,a2+b2=c2. ( )
2.直角三角形两直角边长都为1, 那么
斜边为2。 ( )
3.三角形ABC中,如果较短的二条边
分别为3和4,那么较长的边是5。 ( )
×
×
×
注意:c可不一定是斜边喔!
定理的结论应该是两直角边的平方和等于斜边的平方!
可要看清楚是不是直角三角形啊!!!
1.在△ABC中,∠C=90°,
(1)若 a=5,b=12,则c=_____;
(2)若 a=15,c=25,则b=_____;
(3)若a:b=3:4,c=10,
则a=___,b=___.
二、计算题
13
20
6
8
2. 如图:∠C=∠ABD=90°,AC=4,BC=3,
BD=12,则AD的长等于 .
3.已知:Rt⊿ABC中, ∠C=90°,
∠B=30°,AC=3cm,求BC的长。
30°
回味无穷
知识象一艘船
让它载着我们
驶向理想的
……
敬请指导
再见
4.等腰三角形的腰长为10,底边上的
高为6,则底边的长为 .
回味无穷
知识象一艘船
让它载着我们
驶向理想的
……
敬请指导
再见
