2021-2022学年华东师大版八年级数学上册13.2 .6 三角形全等的判定课件(HL)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册13.2 .6 三角形全等的判定课件(HL) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
13.2 三角形全等的判定课件
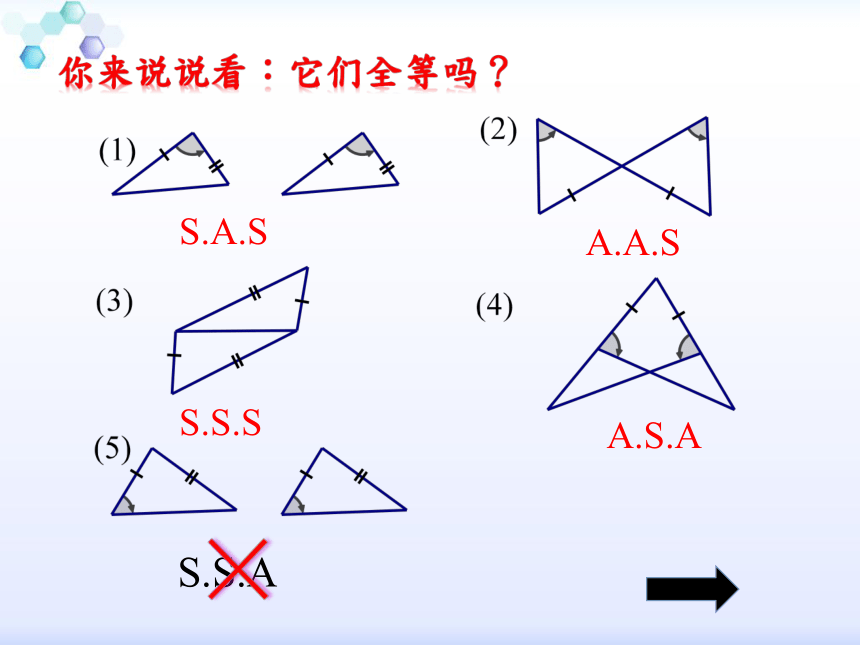
你来说说看:它们全等吗?
S.A.S
A.A.S
S.S.S
A.S.A
S.S.A
×
提出猜想:
S.S.A适用于直角三角形全等的判定。
已知:∠MCN=90°,请以C为直角顶点,作一个直角三角形 ABC,满足CB=a,AB=b。
动手实践
a
b
M
C
N
13.2.6 斜边直角边
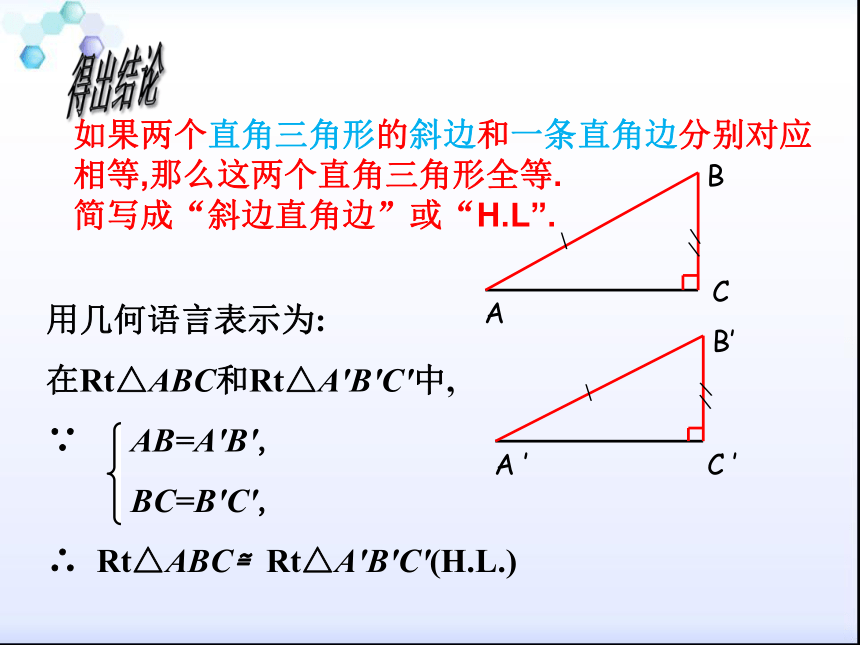
如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等. 简写成“斜边直角边”或“H.L”.
得出结论
A
B
C
A ′
B′
C ′
用几何语言表示为:
在Rt△ABC和Rt△A'B'C'中,
∵ AB=A'B',
BC=B'C',
∴ Rt△ABC≌Rt△A'B'C'(H.L.)
\
\
\
\
\
\
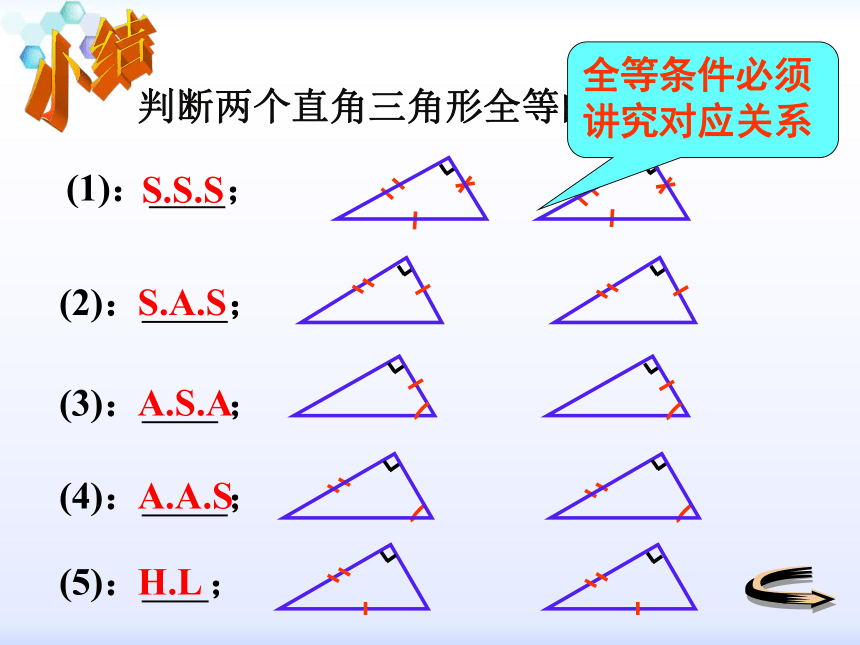
判断两个直角三角形全等的方法有:
(1): ;
(2): ;
(3): ;
(4): ;
S.S.S
S.A.S
A.S.A
A.A.S
(5): ;
H.L
小结
全等条件必须讲究对应关系
例1.已知如图,AC与BD相交于点O,AD=BC,∠C=∠D=90°
求证:AC=BD。
A
B
D
C
O
你还有别的方法吗
证明:在△AOD与△BOC中
∠D=∠C
∠AOD=∠BOC
AD=BC
∴ △AOD ≌ △BOC .(A.A.S.)
∴ OD=OC,OA=OB
∵ OA+OC=AC, OB+OD=BD
∴ AC=BD.
∵
动动脑 如图,AC=AD, ∠C=∠D=90°,
求证: BC=BD
证明:连结AB
∵ ∠C=∠D=90°
∴ △ABC与△ABD都是直角三角形。
在Rt△ABC与Rt△ABD中
∵ AB=AB
AC=AD
∴Rt△ABC≌ Rt△ABD(H.L.)
∴BC=BD(全等三角形对应边相等)
如图,AC=AD, ∠C=∠D=90°,E,F分别是BC,BD上一点,且AE=AF。
求证: BE=BF
例2:
1.如图1,△ABC中,AB=AC,AD是高,
则△ADB与△ADC 填“全等”或“不全等” ,根据_____
2. 如图2,∠B=∠D=90°BC=CD,∠1=50 ° ,则∠2=( ) A.40 ° B.50 ° C.60 ° D.75 °
3.已知:如图3 , AC⊥BC于C , DE⊥AC于E , AD⊥AB于A ,
BC=AE.若AB=5 , 则AD=___________.
图1 图2 图3
4.判断两个直角三角形全等的条件不正确的是( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等 D. 两边对应相等
全等
H.L
学习反馈
D
A
5
5.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由.
知识大盘点
任意三角形 全等的判定方法:
(1).S.S.S
(2).S.A.S
(3).A.S.A
(4).A.A.S
直角三角形 全等专属
(5).H.L
适用于直角三角形
学习要一步一个脚印
孩子们:你们是最棒的!
13.2 三角形全等的判定课件
你来说说看:它们全等吗?
S.A.S
A.A.S
S.S.S
A.S.A
S.S.A
×
提出猜想:
S.S.A适用于直角三角形全等的判定。
已知:∠MCN=90°,请以C为直角顶点,作一个直角三角形 ABC,满足CB=a,AB=b。
动手实践
a
b
M
C
N
13.2.6 斜边直角边
如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等. 简写成“斜边直角边”或“H.L”.
得出结论
A
B
C
A ′
B′
C ′
用几何语言表示为:
在Rt△ABC和Rt△A'B'C'中,
∵ AB=A'B',
BC=B'C',
∴ Rt△ABC≌Rt△A'B'C'(H.L.)
\
\
\
\
\
\
判断两个直角三角形全等的方法有:
(1): ;
(2): ;
(3): ;
(4): ;
S.S.S
S.A.S
A.S.A
A.A.S
(5): ;
H.L
小结
全等条件必须讲究对应关系
例1.已知如图,AC与BD相交于点O,AD=BC,∠C=∠D=90°
求证:AC=BD。
A
B
D
C
O
你还有别的方法吗
证明:在△AOD与△BOC中
∠D=∠C
∠AOD=∠BOC
AD=BC
∴ △AOD ≌ △BOC .(A.A.S.)
∴ OD=OC,OA=OB
∵ OA+OC=AC, OB+OD=BD
∴ AC=BD.
∵
动动脑 如图,AC=AD, ∠C=∠D=90°,
求证: BC=BD
证明:连结AB
∵ ∠C=∠D=90°
∴ △ABC与△ABD都是直角三角形。
在Rt△ABC与Rt△ABD中
∵ AB=AB
AC=AD
∴Rt△ABC≌ Rt△ABD(H.L.)
∴BC=BD(全等三角形对应边相等)
如图,AC=AD, ∠C=∠D=90°,E,F分别是BC,BD上一点,且AE=AF。
求证: BE=BF
例2:
1.如图1,△ABC中,AB=AC,AD是高,
则△ADB与△ADC 填“全等”或“不全等” ,根据_____
2. 如图2,∠B=∠D=90°BC=CD,∠1=50 ° ,则∠2=( ) A.40 ° B.50 ° C.60 ° D.75 °
3.已知:如图3 , AC⊥BC于C , DE⊥AC于E , AD⊥AB于A ,
BC=AE.若AB=5 , 则AD=___________.
图1 图2 图3
4.判断两个直角三角形全等的条件不正确的是( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等 D. 两边对应相等
全等
H.L
学习反馈
D
A
5
5.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由.
知识大盘点
任意三角形 全等的判定方法:
(1).S.S.S
(2).S.A.S
(3).A.S.A
(4).A.A.S
直角三角形 全等专属
(5).H.L
适用于直角三角形
学习要一步一个脚印
孩子们:你们是最棒的!
