第十三章 轴对称等腰三角形、最短路径问题 综合复习(含解析)
文档属性
| 名称 | 第十三章 轴对称等腰三角形、最短路径问题 综合复习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 13:38:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
等腰三角形、最短路径问题
一.等腰三角形
1.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为( )
A.5 B.8 C.10 D.10
2.如图,AD是等边△ABC的一条中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
3.如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则OM为( )
A.2cm B.3cm C.4cm D.1cm
4.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m° B.180°﹣2m° C.30°+m° D.m°
5.如图,在边长为4的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,连接DF,则DF的长为 .
6.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 .
7.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 .
8.如图,在△ABC中,AB=AC,∠A=120°,BC=15cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 cm.
求证:等腰锐角三角形腰上的高与底边的夹角等于顶角的一半.
已知等腰三角形一边上的高与另一边的夹角为20°,求这个等腰三角形顶角的度数?(画出符合题意的图形,直接写出答案即可)
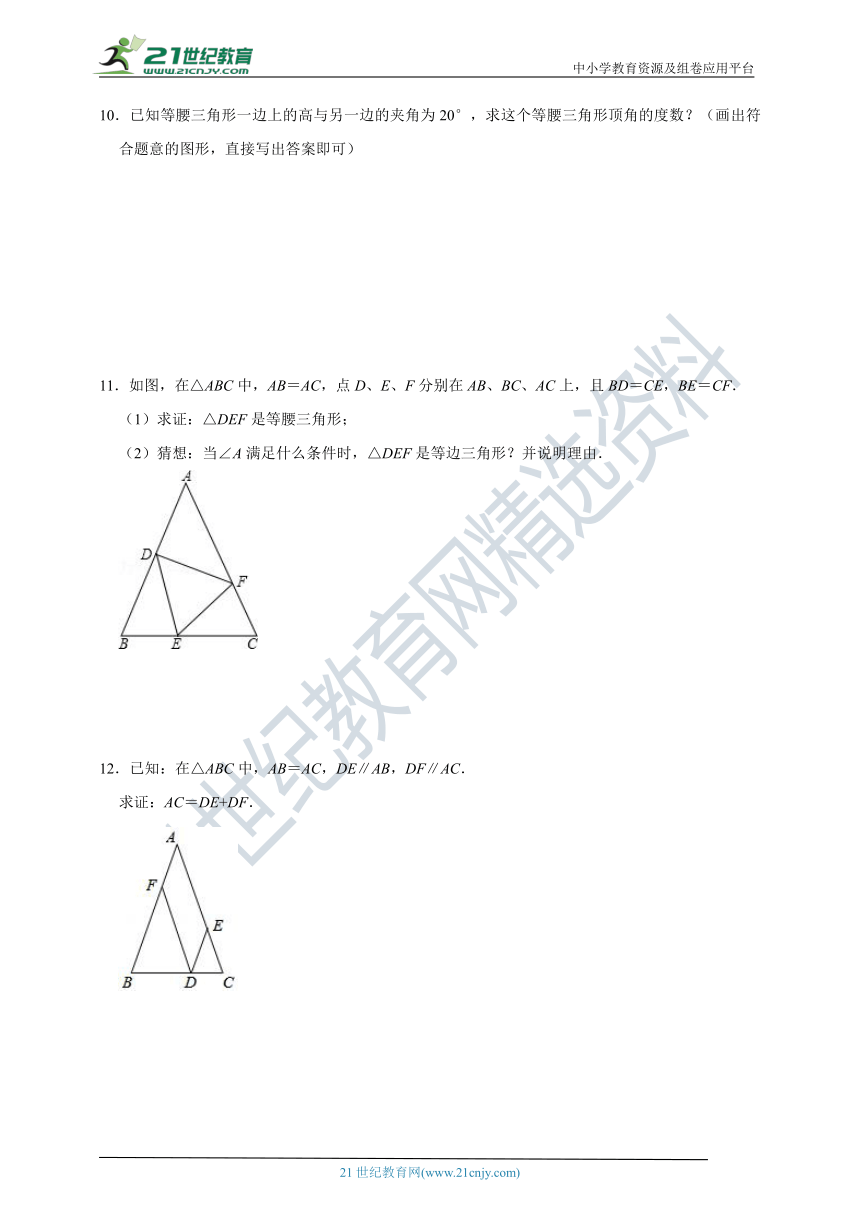
11.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
12.已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
求证:AC=DE+DF.
二.最短路径
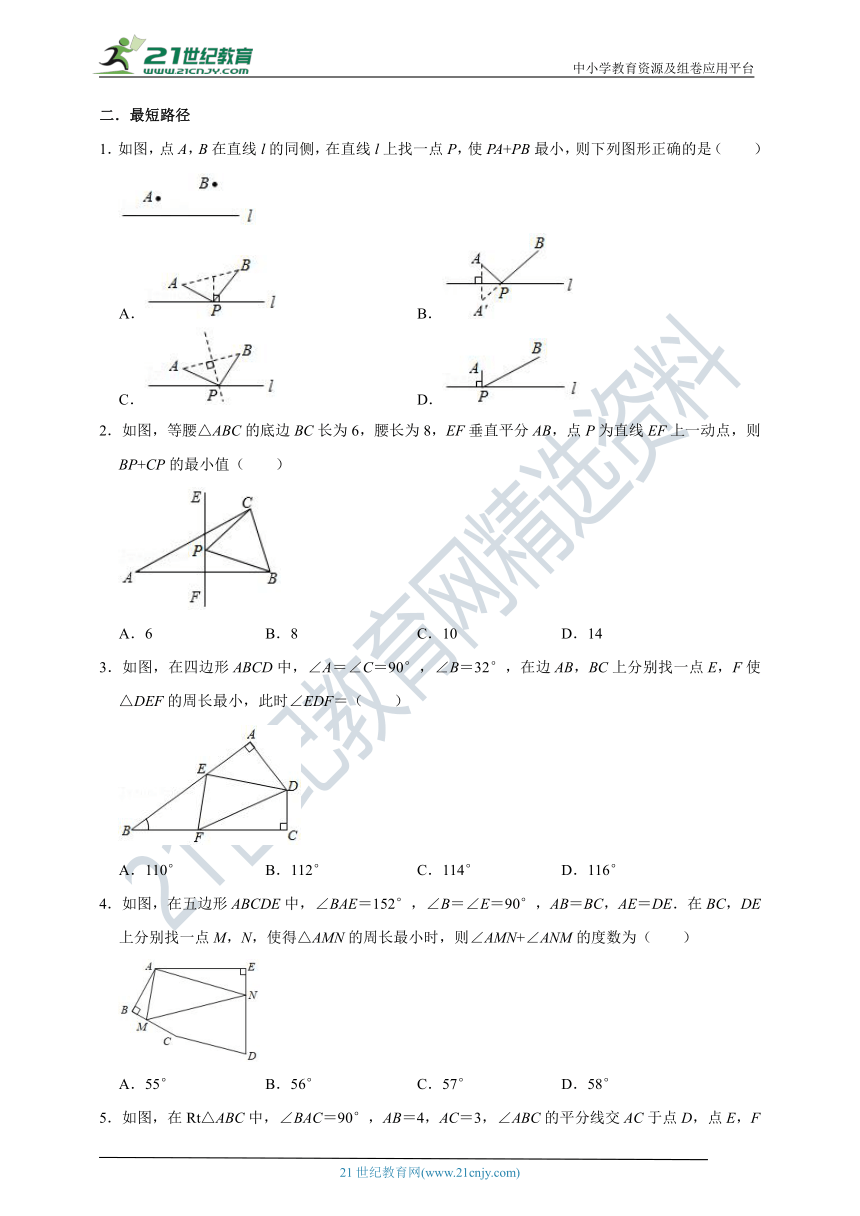
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6 B.8 C.10 D.14
3.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
4.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55° B.56° C.57° D.58°
5.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.1 B.2 C.3 D.4
7.等腰三角形ABC的底边BC长为6,面积是21,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
8.如图,四边形ABCD中,∠C=58°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为 .
9.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为 .
10.如图等腰三角形ABC的底边BC长为6,面积是24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
11.如图,在Rt△ABC中,∠ACB=90°,CM平分∠ACB,点D为CM上一点,点P为边AC上一动点(不与点A,C重合),连结DP,BP.已知CD=BC,当DP+BP的值最小时,∠CDP的度数为 .
12.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得PA+PB的值最小,画出图形并证明.
13.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
14.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,DF是线段AC的垂直平分线;交AC边于点D,交AB边于点E,以BE为边作等边△BEF,连接CF、AF.
(1)求证:△ACF是等边三角形;
(2)若点P是直线DE上一动点,连接BP、CP,当点P运动到何处时,BP+CP的值最小?并求出该最小值.
参考答案与试题解析
一.等腰三角形
1.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为( )
A.5 B.8 C.10 D.10
【解答】解:∵在△ABC中,AB=BC=10,∠A=36°,
∴∠C=∠A=36°,
∵AB的垂直平分线是DE,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=108°﹣36°=72°,
∵∠BEC=∠A+∠ABE=72°
∴∠BEC=∠EBC,
∴CE=BC=10,
故选:C.
2.如图,AD是等边△ABC的一条中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
【解答】解:∵△ABC为等边三角形,
∴∠BAC=60°,
∵AD是等边△ABC的一条中线,
∴AD⊥BC,∠CAD=∠BAC=30°,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠AED+∠CAD=180°,
∴∠ADE=75°,
∴∠EDC=90°﹣75°=15°,
故选:D.
3.如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则OM为( )
A.2cm B.3cm C.4cm D.1cm
【解答】解:过P作PD⊥OB于D,
∵PM=PN,MN=2cm,
∴MD=ND=1(cm),
∵PD⊥OB,
∴∠PDO=90°,
∵∠POB=60°,
∴∠OPD=30°,
∴OD=OP,
∵OP=8cm,
∴OD=4(cm),
∴OM=OD﹣MD=3(cm),
故选:B.
4.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m° B.180°﹣2m° C.30°+m° D.m°
【解答】解:∵AD垂直平分BE,
∴AB=AE,
∴∠ABE=∠AEB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
∴∠BEC=∠BEA+∠ACE,
∵∠BAC=m°,
∴∠ABC+∠ACB=180°﹣m°,
∴∠BEC=(180°﹣∠ABC﹣∠ACB)=[180°﹣(∠ABC+∠ACB)]=[180°﹣(180°﹣m°)]=m°,
故选:D.
5.如图,在边长为4的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,连接DF,则DF的长为 .
【解答】解:如图,过点D作DH⊥AC于H.
∵△ABC是等边三角形,
∴AB=AC=BC=4,∠A=∠C=60°,
∵AD=DB=2,BE=EC=2,
∴AH=AD cos60°=1,DH=AH=,CF=CE cos60°=1,
∴FH=AC﹣AH=CF=4﹣1﹣2=2,
∴DF===.
故答案为:.
6.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 45°或36° .
【解答】解:∵AD平分∠BAC,
∴∠BAD=∠CAD=α,
∵AB=AC,
∴∠ABC=∠C==90°﹣α,
∵PD垂直平分AB,
∴AD=BD,
∴∠ABD=∠BAD=α,
∠EBC=∠ABC﹣∠ABE=90°﹣2α,
∴∠BEC=∠ABE+∠BAC=3α,
当BE=BC时,
∠BEC=∠C,即90°﹣α=3α,
解得α=22.5°,
∴∠BAC=2α=45°;
当BE=CE时,
∠EBC=∠C,此时点E和点A重合,舍去;
当CE=BC时,
∠BEC=∠EBC,即90°﹣2α=3α,
解得α=18°,
∴∠BAC=2α=36°.
故∠BAC的度数为45°或36°.
故答案为:45°或36°.
7.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 5cm .
【解答】解:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠ABF=∠DFB,
∴BD=DF=8cm,
同理,CE=EF,
∵EF=DF﹣DE=5cm,
∴CE=5cm,
故答案为:5cm.
8.如图,在△ABC中,AB=AC,∠A=120°,BC=15cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 5 cm.
【解答】解:
连接AM、AN、过A作AD⊥BC于D,
∵在△ABC中,AB=AC,∠A=120°,BC=15cm,
∴∠B=∠C=30°,BD=CD=7.5cm,
∴AB==5cm=AC,
∵AB的垂直平分线EM,
∴BE=AB=cm
同理CF=cm,
∴BM==5cm,
同理CN=5cm,
∴MN=BC﹣BM﹣CN=5cm,
故答案是:5.
9.求证:等腰锐角三角形腰上的高与底边的夹角等于顶角的一半.
【解答】证明:如图:△ABC是等腰锐角三角形,AB=AC,BD是腰AC上的高.
过点A作AE⊥BC于点E,
∴∠EAC+∠C=90°,
∵BD⊥AC,
∴∠DBC+∠C=90°,
∴∠DBC=∠EAC,
∵AB=AC,AE⊥BC,
∴∠EAC=∠BAC,
∴∠DBC=∠BAC.
10.已知等腰三角形一边上的高与另一边的夹角为20°,求这个等腰三角形顶角的度数?(画出符合题意的图形,直接写出答案即可)
【解答】解:此题要分情况讨论:当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣20°=70°;
或顶角是180°﹣(90°﹣20°)×2=40°;
底上的高在其内部,
故顶角是20°×2=40°.
当等腰三角形的顶角是钝角时,腰上的高在外部.
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°.
故这个等腰三角形顶角的度数为70°或40°或110°.
11.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF,
∴DE=FE,
∴△DEF是等腰三角形;
(2)当∠A=60°时,△DEF是等边三角形,
理由:∵△BDE≌△CEF,
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B
要△DEF是等边三角形,只要∠DEF=60°.
所以,当∠A=60°时,∠B=∠DEF=60°,
则△DEF是等边三角形.
12.已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
求证:AC=DE+DF.
【解答】证明:∵DE∥AB,
∴∠B=∠EDC,
∵AB=AC,
∴∠B=∠C,
∴∠EDC=∠C,
∴ED=EC,
∵DE∥AB,DF∥AC,
∴四边形AFDE为平行四边形,
∴DF=EA,
∴AC=AE+EC=DE+DF.
二.最短路径
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
【解答】解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
∴PA+PB=PA′+PB=A′B为最小,
故选:B.
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6 B.8 C.10 D.14
【解答】解:连接AP,
∵EF垂直平分AB,
∴AP=BP,
∴BP+CP≥AC,
∴当PB+CP=AC时,BP+CP值最小,
∵等腰△ABC腰长为8,
∴AC=8,
∴BP+CP的最小值为8,
故选:B.
3.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【解答】解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α,
∴∠ADC=180°﹣α,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣64°
=116°.
故选:D.
4.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55° B.56° C.57° D.58°
【解答】解:如图,延长AB至A′,使A′B=AB,
延长AE至A″,使A″E=AE,
则BC垂直平分AA′,DE垂直平分AA″,
∴AM=A′M,AN=A″N,
根据两点之间,线段最短,
当A′,M,N,A″四点在一条直线时,A′M+MN+NA″最小,
则AM+MN+AN的值最小,
即△AMN的周长最小,
∵AM=A′M,AN=A″N,
∴可设∠MAA′=∠MA′A=x,∠NAA″=∠NA″A=y,
在△AA′A″中,x+y=180°﹣∠BAE=180°﹣152°=28°,
∵∠AMN=∠MAA′+∠MA′A=2x,∠ANM=2y,
∴∠AMN+∠ANM=2x+2y=56°,
故选:B.
5.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
【解答】解:作点A关于BD的对称点M,
∵BD平分∠ABC,
∴M落在BC上.
∴BM=BA=4,
过M作MF⊥AB于F,交BD于E,
则AE+EF的最小值是MF的长.
∵∠MFB=∠CAB=90°,
∴MF∥CA,
∴,
即,MF=2.4,
∴AE+EF=MF=2.4.
故选:B.
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.1 B.2 C.3 D.4
【解答】解:作AH⊥OB于H,交OC于P,作PQ⊥OA于Q,
∵∠OAB=∠AOB=15°,
∴PH=PQ,
∴PA+PQ=PA+PH=AH,
∴PA+PQ的最小值为AH,
在Rt△ABH中,∵OB=AB=6,∠ABH=30°,
∴AH=AB=3,
∴PA+PQ的最小值为3,
故选:C.
7.等腰三角形ABC的底边BC长为6,面积是21,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 10 .
【解答】解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×6×AD=21,
∴AD=7,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短为AD+BD=AD+BC=10,
故答案为:10.
8.如图,四边形ABCD中,∠C=58°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为 64° .
【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=58°,
∴∠DAB=122°,
∴∠HAA′=58°,
∴∠AA′E+∠A″=∠HAA′=58°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=58°,
∴∠EAF=122°﹣58°=64°,
故答案为:64°.
9.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为 10 .
【解答】解:∵直线m是△ABC中BC边的垂直平分线,
∴BP=CP,
∴△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC,
∴当A、B、P三点共线时,△ACP的周长最小,
∵AB=6,BC=7,AC=4,
∴△ACP的周长6+4=10,
∴△ACP的周长最小值为10,
故答案为10.
10.如图等腰三角形ABC的底边BC长为6,面积是24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 11 .
【解答】解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×6×AD=24,
∴AD=8,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短为AD+BD=AD+BC=11,
故答案为:11.
11.如图,在Rt△ABC中,∠ACB=90°,CM平分∠ACB,点D为CM上一点,点P为边AC上一动点(不与点A,C重合),连结DP,BP.已知CD=BC,当DP+BP的值最小时,∠CDP的度数为 22.5 .
【解答】解:如图,作点B关于AC的对称点B′,连接DB′交AC于点P,当D,P,B′共线时,PD+PB的值最小.
∵∠ACB=90°,CM平分∠ACB,
∴∠DCB=×90°=45°,
∵CB=CB′,CD=CB,
∴CD=CB′,
∴∠CDB′=∠B′,
∵∠DCB=∠CDB′+∠B′,
∴∠CDP=22.5°,
故答案为:22.5.
12.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得PA+PB的值最小,画出图形并证明.
【解答】解:如图所示,作点B关于直线l的对称点B',连接AB',交直线l于点P,连接BP,
则BP=B'P,
∴AP+BP=AP+B'P=AB',
∴PA+PB的值最小等于线段AB'的长,
13.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
【解答】解:(1)∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,
∴∠AEF=∠FEC,
∵∠ACB=∠AFE=90°,
∴DE∥BC,
∴∠AEF=∠EBC,∠FEC=∠ECB,
∴∠ECB=∠EBC,
∴CE=BE;
(2)连接PA,PC,
∵DE垂直平分AC,P在DE上,
∴PC=PA,
∵两点之间线段最短,
∴当P与E重合时PA+PB最小为15 cm,
∴PB+PC最小为15 cm.
14.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,DF是线段AC的垂直平分线;交AC边于点D,交AB边于点E,以BE为边作等边△BEF,连接CF、AF.
(1)求证:△ACF是等边三角形;
(2)若点P是直线DE上一动点,连接BP、CP,当点P运动到何处时,BP+CP的值最小?并求出该最小值.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,
∵FD是线段AC的垂直平分线,
∴FD⊥AC,CD=AD,
∴CF=AF,
∵∠ACB=∠ADF=90°,
∴FD∥BC,
∴BE=AE,
∵△BEF是等边三角形,
∴∠ABF=∠BEF=60°,BE=EF,
∴EF=AE,
∴∠EAF=∠EFA,
∴2∠EAF=∠BEF=60°,
∴∠EAF=30°,
∴∠CAF=∠BAC+∠EAF=60°,
∴△ACF是等边三角形;
(2)解:∵FD是AC的垂直平分线,
∴PA=PC,
∴BP+PC=BP+PA,
∵BP+PA≥AB,
∴当点P运动到点E处时,BP+CP的值最小,最小值为AB.
在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,
∴AB=2BC=6,
∴BP+CP的最小值为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
等腰三角形、最短路径问题
一.等腰三角形
1.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为( )
A.5 B.8 C.10 D.10
2.如图,AD是等边△ABC的一条中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
3.如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则OM为( )
A.2cm B.3cm C.4cm D.1cm
4.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m° B.180°﹣2m° C.30°+m° D.m°
5.如图,在边长为4的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,连接DF,则DF的长为 .
6.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 .
7.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 .
8.如图,在△ABC中,AB=AC,∠A=120°,BC=15cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 cm.
求证:等腰锐角三角形腰上的高与底边的夹角等于顶角的一半.
已知等腰三角形一边上的高与另一边的夹角为20°,求这个等腰三角形顶角的度数?(画出符合题意的图形,直接写出答案即可)
11.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
12.已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
求证:AC=DE+DF.
二.最短路径
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6 B.8 C.10 D.14
3.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
4.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55° B.56° C.57° D.58°
5.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.1 B.2 C.3 D.4
7.等腰三角形ABC的底边BC长为6,面积是21,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
8.如图,四边形ABCD中,∠C=58°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为 .
9.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为 .
10.如图等腰三角形ABC的底边BC长为6,面积是24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
11.如图,在Rt△ABC中,∠ACB=90°,CM平分∠ACB,点D为CM上一点,点P为边AC上一动点(不与点A,C重合),连结DP,BP.已知CD=BC,当DP+BP的值最小时,∠CDP的度数为 .
12.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得PA+PB的值最小,画出图形并证明.
13.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
14.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,DF是线段AC的垂直平分线;交AC边于点D,交AB边于点E,以BE为边作等边△BEF,连接CF、AF.
(1)求证:△ACF是等边三角形;
(2)若点P是直线DE上一动点,连接BP、CP,当点P运动到何处时,BP+CP的值最小?并求出该最小值.
参考答案与试题解析
一.等腰三角形
1.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为( )
A.5 B.8 C.10 D.10
【解答】解:∵在△ABC中,AB=BC=10,∠A=36°,
∴∠C=∠A=36°,
∵AB的垂直平分线是DE,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=108°﹣36°=72°,
∵∠BEC=∠A+∠ABE=72°
∴∠BEC=∠EBC,
∴CE=BC=10,
故选:C.
2.如图,AD是等边△ABC的一条中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
【解答】解:∵△ABC为等边三角形,
∴∠BAC=60°,
∵AD是等边△ABC的一条中线,
∴AD⊥BC,∠CAD=∠BAC=30°,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠AED+∠CAD=180°,
∴∠ADE=75°,
∴∠EDC=90°﹣75°=15°,
故选:D.
3.如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则OM为( )
A.2cm B.3cm C.4cm D.1cm
【解答】解:过P作PD⊥OB于D,
∵PM=PN,MN=2cm,
∴MD=ND=1(cm),
∵PD⊥OB,
∴∠PDO=90°,
∵∠POB=60°,
∴∠OPD=30°,
∴OD=OP,
∵OP=8cm,
∴OD=4(cm),
∴OM=OD﹣MD=3(cm),
故选:B.
4.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m° B.180°﹣2m° C.30°+m° D.m°
【解答】解:∵AD垂直平分BE,
∴AB=AE,
∴∠ABE=∠AEB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
∴∠BEC=∠BEA+∠ACE,
∵∠BAC=m°,
∴∠ABC+∠ACB=180°﹣m°,
∴∠BEC=(180°﹣∠ABC﹣∠ACB)=[180°﹣(∠ABC+∠ACB)]=[180°﹣(180°﹣m°)]=m°,
故选:D.
5.如图,在边长为4的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,连接DF,则DF的长为 .
【解答】解:如图,过点D作DH⊥AC于H.
∵△ABC是等边三角形,
∴AB=AC=BC=4,∠A=∠C=60°,
∵AD=DB=2,BE=EC=2,
∴AH=AD cos60°=1,DH=AH=,CF=CE cos60°=1,
∴FH=AC﹣AH=CF=4﹣1﹣2=2,
∴DF===.
故答案为:.
6.如图,在△ABC中,AB=AC,AD平分∠BAC,PD垂直平分AB,连接BD并延长,交边AC于点E.若△BCE是等腰三角形,则∠BAC的度数为 45°或36° .
【解答】解:∵AD平分∠BAC,
∴∠BAD=∠CAD=α,
∵AB=AC,
∴∠ABC=∠C==90°﹣α,
∵PD垂直平分AB,
∴AD=BD,
∴∠ABD=∠BAD=α,
∠EBC=∠ABC﹣∠ABE=90°﹣2α,
∴∠BEC=∠ABE+∠BAC=3α,
当BE=BC时,
∠BEC=∠C,即90°﹣α=3α,
解得α=22.5°,
∴∠BAC=2α=45°;
当BE=CE时,
∠EBC=∠C,此时点E和点A重合,舍去;
当CE=BC时,
∠BEC=∠EBC,即90°﹣2α=3α,
解得α=18°,
∴∠BAC=2α=36°.
故∠BAC的度数为45°或36°.
故答案为:45°或36°.
7.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F,过F作DF∥BC交AB于D,若BD=8cm,DE=3cm,则CE的长为 5cm .
【解答】解:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠ABF=∠DFB,
∴BD=DF=8cm,
同理,CE=EF,
∵EF=DF﹣DE=5cm,
∴CE=5cm,
故答案为:5cm.
8.如图,在△ABC中,AB=AC,∠A=120°,BC=15cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 5 cm.
【解答】解:
连接AM、AN、过A作AD⊥BC于D,
∵在△ABC中,AB=AC,∠A=120°,BC=15cm,
∴∠B=∠C=30°,BD=CD=7.5cm,
∴AB==5cm=AC,
∵AB的垂直平分线EM,
∴BE=AB=cm
同理CF=cm,
∴BM==5cm,
同理CN=5cm,
∴MN=BC﹣BM﹣CN=5cm,
故答案是:5.
9.求证:等腰锐角三角形腰上的高与底边的夹角等于顶角的一半.
【解答】证明:如图:△ABC是等腰锐角三角形,AB=AC,BD是腰AC上的高.
过点A作AE⊥BC于点E,
∴∠EAC+∠C=90°,
∵BD⊥AC,
∴∠DBC+∠C=90°,
∴∠DBC=∠EAC,
∵AB=AC,AE⊥BC,
∴∠EAC=∠BAC,
∴∠DBC=∠BAC.
10.已知等腰三角形一边上的高与另一边的夹角为20°,求这个等腰三角形顶角的度数?(画出符合题意的图形,直接写出答案即可)
【解答】解:此题要分情况讨论:当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣20°=70°;
或顶角是180°﹣(90°﹣20°)×2=40°;
底上的高在其内部,
故顶角是20°×2=40°.
当等腰三角形的顶角是钝角时,腰上的高在外部.
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°.
故这个等腰三角形顶角的度数为70°或40°或110°.
11.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF,
∴DE=FE,
∴△DEF是等腰三角形;
(2)当∠A=60°时,△DEF是等边三角形,
理由:∵△BDE≌△CEF,
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B
要△DEF是等边三角形,只要∠DEF=60°.
所以,当∠A=60°时,∠B=∠DEF=60°,
则△DEF是等边三角形.
12.已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
求证:AC=DE+DF.
【解答】证明:∵DE∥AB,
∴∠B=∠EDC,
∵AB=AC,
∴∠B=∠C,
∴∠EDC=∠C,
∴ED=EC,
∵DE∥AB,DF∥AC,
∴四边形AFDE为平行四边形,
∴DF=EA,
∴AC=AE+EC=DE+DF.
二.最短路径
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
【解答】解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
∴PA+PB=PA′+PB=A′B为最小,
故选:B.
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6 B.8 C.10 D.14
【解答】解:连接AP,
∵EF垂直平分AB,
∴AP=BP,
∴BP+CP≥AC,
∴当PB+CP=AC时,BP+CP值最小,
∵等腰△ABC腰长为8,
∴AC=8,
∴BP+CP的最小值为8,
故选:B.
3.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【解答】解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α,
∴∠ADC=180°﹣α,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣64°
=116°.
故选:D.
4.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55° B.56° C.57° D.58°
【解答】解:如图,延长AB至A′,使A′B=AB,
延长AE至A″,使A″E=AE,
则BC垂直平分AA′,DE垂直平分AA″,
∴AM=A′M,AN=A″N,
根据两点之间,线段最短,
当A′,M,N,A″四点在一条直线时,A′M+MN+NA″最小,
则AM+MN+AN的值最小,
即△AMN的周长最小,
∵AM=A′M,AN=A″N,
∴可设∠MAA′=∠MA′A=x,∠NAA″=∠NA″A=y,
在△AA′A″中,x+y=180°﹣∠BAE=180°﹣152°=28°,
∵∠AMN=∠MAA′+∠MA′A=2x,∠ANM=2y,
∴∠AMN+∠ANM=2x+2y=56°,
故选:B.
5.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
【解答】解:作点A关于BD的对称点M,
∵BD平分∠ABC,
∴M落在BC上.
∴BM=BA=4,
过M作MF⊥AB于F,交BD于E,
则AE+EF的最小值是MF的长.
∵∠MFB=∠CAB=90°,
∴MF∥CA,
∴,
即,MF=2.4,
∴AE+EF=MF=2.4.
故选:B.
6.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A.1 B.2 C.3 D.4
【解答】解:作AH⊥OB于H,交OC于P,作PQ⊥OA于Q,
∵∠OAB=∠AOB=15°,
∴PH=PQ,
∴PA+PQ=PA+PH=AH,
∴PA+PQ的最小值为AH,
在Rt△ABH中,∵OB=AB=6,∠ABH=30°,
∴AH=AB=3,
∴PA+PQ的最小值为3,
故选:C.
7.等腰三角形ABC的底边BC长为6,面积是21,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 10 .
【解答】解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×6×AD=21,
∴AD=7,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短为AD+BD=AD+BC=10,
故答案为:10.
8.如图,四边形ABCD中,∠C=58°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为 64° .
【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=58°,
∴∠DAB=122°,
∴∠HAA′=58°,
∴∠AA′E+∠A″=∠HAA′=58°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=58°,
∴∠EAF=122°﹣58°=64°,
故答案为:64°.
9.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为 10 .
【解答】解:∵直线m是△ABC中BC边的垂直平分线,
∴BP=CP,
∴△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC,
∴当A、B、P三点共线时,△ACP的周长最小,
∵AB=6,BC=7,AC=4,
∴△ACP的周长6+4=10,
∴△ACP的周长最小值为10,
故答案为10.
10.如图等腰三角形ABC的底边BC长为6,面积是24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 11 .
【解答】解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×6×AD=24,
∴AD=8,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短为AD+BD=AD+BC=11,
故答案为:11.
11.如图,在Rt△ABC中,∠ACB=90°,CM平分∠ACB,点D为CM上一点,点P为边AC上一动点(不与点A,C重合),连结DP,BP.已知CD=BC,当DP+BP的值最小时,∠CDP的度数为 22.5 .
【解答】解:如图,作点B关于AC的对称点B′,连接DB′交AC于点P,当D,P,B′共线时,PD+PB的值最小.
∵∠ACB=90°,CM平分∠ACB,
∴∠DCB=×90°=45°,
∵CB=CB′,CD=CB,
∴CD=CB′,
∴∠CDB′=∠B′,
∵∠DCB=∠CDB′+∠B′,
∴∠CDP=22.5°,
故答案为:22.5.
12.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得PA+PB的值最小,画出图形并证明.
【解答】解:如图所示,作点B关于直线l的对称点B',连接AB',交直线l于点P,连接BP,
则BP=B'P,
∴AP+BP=AP+B'P=AB',
∴PA+PB的值最小等于线段AB'的长,
13.如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.
(1)求证:CE=BE.
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.
【解答】解:(1)∵△ACD为等边三角形,DE⊥AC,
∴DE垂直平分AC,
∴∠AEF=∠FEC,
∵∠ACB=∠AFE=90°,
∴DE∥BC,
∴∠AEF=∠EBC,∠FEC=∠ECB,
∴∠ECB=∠EBC,
∴CE=BE;
(2)连接PA,PC,
∵DE垂直平分AC,P在DE上,
∴PC=PA,
∵两点之间线段最短,
∴当P与E重合时PA+PB最小为15 cm,
∴PB+PC最小为15 cm.
14.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,DF是线段AC的垂直平分线;交AC边于点D,交AB边于点E,以BE为边作等边△BEF,连接CF、AF.
(1)求证:△ACF是等边三角形;
(2)若点P是直线DE上一动点,连接BP、CP,当点P运动到何处时,BP+CP的值最小?并求出该最小值.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,
∵FD是线段AC的垂直平分线,
∴FD⊥AC,CD=AD,
∴CF=AF,
∵∠ACB=∠ADF=90°,
∴FD∥BC,
∴BE=AE,
∵△BEF是等边三角形,
∴∠ABF=∠BEF=60°,BE=EF,
∴EF=AE,
∴∠EAF=∠EFA,
∴2∠EAF=∠BEF=60°,
∴∠EAF=30°,
∴∠CAF=∠BAC+∠EAF=60°,
∴△ACF是等边三角形;
(2)解:∵FD是AC的垂直平分线,
∴PA=PC,
∴BP+PC=BP+PA,
∵BP+PA≥AB,
∴当点P运动到点E处时,BP+CP的值最小,最小值为AB.
在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3,
∴AB=2BC=6,
∴BP+CP的最小值为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
