湘教版初中数学七年级上册 3.4一元一次方程模型的应用--和差倍分问题课件(共20张PPT)
文档属性
| 名称 | 湘教版初中数学七年级上册 3.4一元一次方程模型的应用--和差倍分问题课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 295.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.4一元一次方程模型的应用
和差倍分问题
之
陈景润是我国有名的数学家。他
不爱逛马路,特别爱数学。学习
起来,常常忘记了吃饭睡觉。有
一次,陈景润边思考问题边走路,
撞到一 树干上,头也不抬说:“对不起,对不起。”继续思考。
数学家的故事
数学小史料
英国伦敦博物馆保存着一部极其珍贵的文物——
纸草书.这是古代埃及人于公元前1700年左右写成.
这部书中记载了许多有关数学的问题.
1、掌握一元一次方程解简单应用题的方法和步骤;并能解答一元一次方程和差倍分问题的简单应用题;
2、通过列方程解应用题,提高分析问题、解决问题的能力;
3、理解和体会数学建模思想在实际问题中的作用,形成数学知识解决问题的意识。
目标导学
一元一次方程的应用(一)
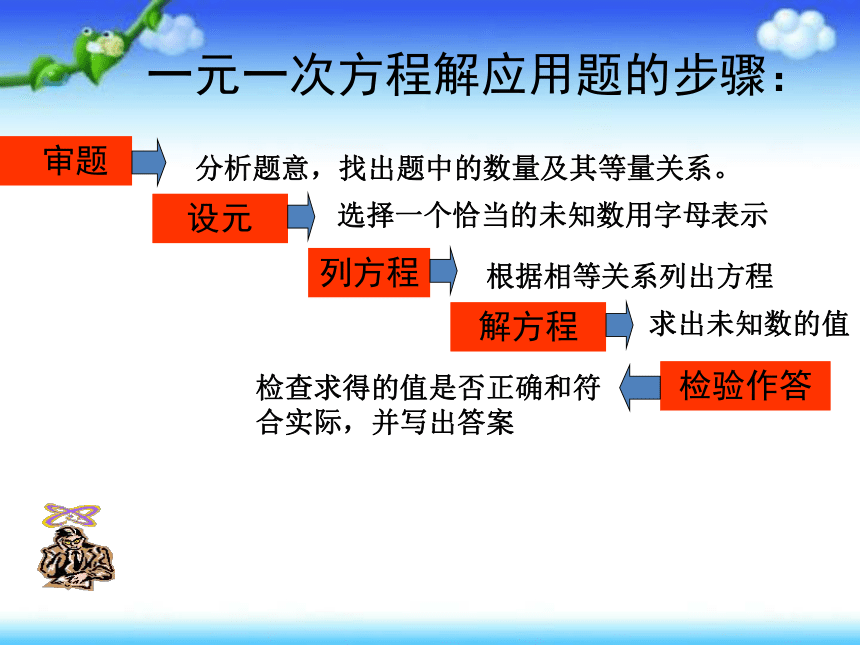
一元一次方程解应用题的步骤:
列方程
解方程
检验作答
设元
审题
分析题意,找出题中的数量及其等量关系。
选择一个恰当的未知数用字母表示
根据相等关系列出方程
求出未知数的值
检查求得的值是否正确和符合实际,并写出答案
我校4位老师带着校足球队全体队员一起去观看一场“颠峰对决”。教师门票按全票价每人100元,学生只收半价,已知共付门票费1000元。你能算出校足球队有多少名队员吗?
情景引入
单张票价 票数量 总票款
全价票 100元/人 4 100×4
半价票 50元/人 x 50x
合计 / 1000
老师的总票价 +
学生的总票价=1000
相等关系
解:设校足球队有x名队员,
依题意得
+50 x
解得 x=12
检验:x=12适合方程,且符合题意
答:校足球队有12名队员。
4×100
=1000
例1:足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3∶5,一个足球表面一共有32个皮块,黑色皮块和白色皮块各有多少个?
解:设黑色皮块有3x个,则白色皮块有5x个,,由题意得
答:黑色皮块有12个,白色皮块有20个.
3x +5x=32
x=4
典例精析
例2:幼儿园某课室有四条腿的椅子和三条腿的凳子共36个,如果椅子腿数和凳子腿数的和为120,有几张椅子和几条凳子?
你能找出题中的哪些已知量?未知量?
你能找出题中的等量关系吗?
(1)椅子数+凳子数=36
(2)椅子腿数+凳子腿数=120
你设哪个未知数为X,并能把找到的等量关系改写成方程吗?
设有X张椅子,则有(36-X)张凳子
例2:幼儿园某课室有四条腿的椅子和三条腿的凳子共36个,如果椅子腿数和凳子腿数的和为120,有几张椅子和几条凳子?
椅子 凳子
数量
腿数
总腿数
X
36-X
4X
4
3
3(36-X)
椅子腿数+凳子腿数=120
解:设有X张椅子,则有(16-X)条凳子,由题意得
4X+3(36-X)=120
解得 x=12
凳子数为36-12=14(条)
答:有12张椅子和14条凳子。
例3:某高校运会上,大一学生A班共获得奖牌76枚,其中金牌是铜牌的2倍少8枚,银牌比铜牌多4枚,请你算一算,A班获得铜牌多少枚?
你能找出题中的哪些已知量?未知量?
你能找出题中的等量关系吗?
你设哪个未知数为X,并能把找到的等量关系改写成方程吗?
等量关系:金牌数+银牌数+铜牌数=奖牌数
设A班获得铜牌X枚,则金牌为(2 X-8)枚,银牌为( X +4)枚
例3:某高校运会上,大一学生A班共获得奖牌88枚,其中金牌是铜牌的2倍少8枚,银牌比铜牌多4枚,请你算一算,A班获得铜牌多少枚?
金牌 银牌 铜牌
数量
等量关系
解:设A班获得铜牌X枚,则金牌为(2X-8)枚,银 牌为(X+4)枚,由题意得
(2X-8)+(X+4)+X=76
解得 X=20
答:A班获得铜牌20枚。
2X-8
X+4
X
金牌数+银牌数+铜牌数=奖牌数
知
识
闯
关
全民答题
一战到底
晋级挑战
一个长方形的周长是62cm,且长比宽多5cm,求长方形的长。
全民答题
解:设长方形的长是Xcm,则宽为(X-5)cm,
由题意得
2[X+(X-5)]=62
X=18
答:长方形的长为18cm
长方形的周长=(长+宽)×2
返回
晋级挑战
一个长方形的周长是62cm,且长与宽的比是2:3,求长方形的长。
解:设长方形的长是2Xcm,则宽为3Xcm,
由题意得
2×(2X+3X)=62
X=6.2
长方形的长为6.2×2=12.4(cm)
答:长方形的宽为12.4cm
返回
双十一后,某物流公司要将300吨物资运往某地,现有A,B两种型号的车可供调用,已知A型车每辆可装20吨,B型车每辆可装10吨,在每辆车不超载的条件下,把300吨物资一次性运完,现有A型,B型车共25辆可调用,并且恰好把物资一次性运完,则A型车有多少辆
一战到底
A型车 B型车
每辆可载重量(吨)
数量(辆)
总量(吨)
等量关系
20
10
20X
10(25-X)
A型车运货总量+B型车运货总量=300
X
25-X
解:设A型车有X辆,由题意得
20X+10(25-X)=300
解得: X=5
答:A型车有5辆。
某车间有22名工人,生产特种螺栓和螺母,一个螺栓的两头各套上一螺母配成一套,每人每天平均生产螺栓12个或螺母20个,问多少工人生产螺栓,多少工人生产螺母,才能使一天所生产的螺栓和螺母正好配套?
解:设x名工人生产螺栓,(22-x)名工人生产螺母,列方程得 2 × 12x=20(22-x)
解得 x=10
生产螺母的人数为 22-x=12
答:10名工人生产螺栓,12名 工人生产螺母,才能使一天所生产的螺栓和螺帽正好配套
知识拓展:
。
当堂检测
1:一个长方形的周长是100cm,且长比宽多5cm,求长方形的宽。
2:一个长方形的周长是80cm,且长与宽的比是3:2,求长方形的长。
3:篮球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,某队在某次比赛中共踢了10场球,其中负4场,共得30分,问这个队共胜了多少场?
课堂小结
本节课你有什么收获?
学会用一元一次方程解应用题
一元一次方程解应用题的基本步骤是什么?
审题、设元、列方程、解方程、检验作答
学会列表格法,理清思路。
谢谢大家!
3.4一元一次方程模型的应用
和差倍分问题
之
陈景润是我国有名的数学家。他
不爱逛马路,特别爱数学。学习
起来,常常忘记了吃饭睡觉。有
一次,陈景润边思考问题边走路,
撞到一 树干上,头也不抬说:“对不起,对不起。”继续思考。
数学家的故事
数学小史料
英国伦敦博物馆保存着一部极其珍贵的文物——
纸草书.这是古代埃及人于公元前1700年左右写成.
这部书中记载了许多有关数学的问题.
1、掌握一元一次方程解简单应用题的方法和步骤;并能解答一元一次方程和差倍分问题的简单应用题;
2、通过列方程解应用题,提高分析问题、解决问题的能力;
3、理解和体会数学建模思想在实际问题中的作用,形成数学知识解决问题的意识。
目标导学
一元一次方程的应用(一)
一元一次方程解应用题的步骤:
列方程
解方程
检验作答
设元
审题
分析题意,找出题中的数量及其等量关系。
选择一个恰当的未知数用字母表示
根据相等关系列出方程
求出未知数的值
检查求得的值是否正确和符合实际,并写出答案
我校4位老师带着校足球队全体队员一起去观看一场“颠峰对决”。教师门票按全票价每人100元,学生只收半价,已知共付门票费1000元。你能算出校足球队有多少名队员吗?
情景引入
单张票价 票数量 总票款
全价票 100元/人 4 100×4
半价票 50元/人 x 50x
合计 / 1000
老师的总票价 +
学生的总票价=1000
相等关系
解:设校足球队有x名队员,
依题意得
+50 x
解得 x=12
检验:x=12适合方程,且符合题意
答:校足球队有12名队员。
4×100
=1000
例1:足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3∶5,一个足球表面一共有32个皮块,黑色皮块和白色皮块各有多少个?
解:设黑色皮块有3x个,则白色皮块有5x个,,由题意得
答:黑色皮块有12个,白色皮块有20个.
3x +5x=32
x=4
典例精析
例2:幼儿园某课室有四条腿的椅子和三条腿的凳子共36个,如果椅子腿数和凳子腿数的和为120,有几张椅子和几条凳子?
你能找出题中的哪些已知量?未知量?
你能找出题中的等量关系吗?
(1)椅子数+凳子数=36
(2)椅子腿数+凳子腿数=120
你设哪个未知数为X,并能把找到的等量关系改写成方程吗?
设有X张椅子,则有(36-X)张凳子
例2:幼儿园某课室有四条腿的椅子和三条腿的凳子共36个,如果椅子腿数和凳子腿数的和为120,有几张椅子和几条凳子?
椅子 凳子
数量
腿数
总腿数
X
36-X
4X
4
3
3(36-X)
椅子腿数+凳子腿数=120
解:设有X张椅子,则有(16-X)条凳子,由题意得
4X+3(36-X)=120
解得 x=12
凳子数为36-12=14(条)
答:有12张椅子和14条凳子。
例3:某高校运会上,大一学生A班共获得奖牌76枚,其中金牌是铜牌的2倍少8枚,银牌比铜牌多4枚,请你算一算,A班获得铜牌多少枚?
你能找出题中的哪些已知量?未知量?
你能找出题中的等量关系吗?
你设哪个未知数为X,并能把找到的等量关系改写成方程吗?
等量关系:金牌数+银牌数+铜牌数=奖牌数
设A班获得铜牌X枚,则金牌为(2 X-8)枚,银牌为( X +4)枚
例3:某高校运会上,大一学生A班共获得奖牌88枚,其中金牌是铜牌的2倍少8枚,银牌比铜牌多4枚,请你算一算,A班获得铜牌多少枚?
金牌 银牌 铜牌
数量
等量关系
解:设A班获得铜牌X枚,则金牌为(2X-8)枚,银 牌为(X+4)枚,由题意得
(2X-8)+(X+4)+X=76
解得 X=20
答:A班获得铜牌20枚。
2X-8
X+4
X
金牌数+银牌数+铜牌数=奖牌数
知
识
闯
关
全民答题
一战到底
晋级挑战
一个长方形的周长是62cm,且长比宽多5cm,求长方形的长。
全民答题
解:设长方形的长是Xcm,则宽为(X-5)cm,
由题意得
2[X+(X-5)]=62
X=18
答:长方形的长为18cm
长方形的周长=(长+宽)×2
返回
晋级挑战
一个长方形的周长是62cm,且长与宽的比是2:3,求长方形的长。
解:设长方形的长是2Xcm,则宽为3Xcm,
由题意得
2×(2X+3X)=62
X=6.2
长方形的长为6.2×2=12.4(cm)
答:长方形的宽为12.4cm
返回
双十一后,某物流公司要将300吨物资运往某地,现有A,B两种型号的车可供调用,已知A型车每辆可装20吨,B型车每辆可装10吨,在每辆车不超载的条件下,把300吨物资一次性运完,现有A型,B型车共25辆可调用,并且恰好把物资一次性运完,则A型车有多少辆
一战到底
A型车 B型车
每辆可载重量(吨)
数量(辆)
总量(吨)
等量关系
20
10
20X
10(25-X)
A型车运货总量+B型车运货总量=300
X
25-X
解:设A型车有X辆,由题意得
20X+10(25-X)=300
解得: X=5
答:A型车有5辆。
某车间有22名工人,生产特种螺栓和螺母,一个螺栓的两头各套上一螺母配成一套,每人每天平均生产螺栓12个或螺母20个,问多少工人生产螺栓,多少工人生产螺母,才能使一天所生产的螺栓和螺母正好配套?
解:设x名工人生产螺栓,(22-x)名工人生产螺母,列方程得 2 × 12x=20(22-x)
解得 x=10
生产螺母的人数为 22-x=12
答:10名工人生产螺栓,12名 工人生产螺母,才能使一天所生产的螺栓和螺帽正好配套
知识拓展:
。
当堂检测
1:一个长方形的周长是100cm,且长比宽多5cm,求长方形的宽。
2:一个长方形的周长是80cm,且长与宽的比是3:2,求长方形的长。
3:篮球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,某队在某次比赛中共踢了10场球,其中负4场,共得30分,问这个队共胜了多少场?
课堂小结
本节课你有什么收获?
学会用一元一次方程解应用题
一元一次方程解应用题的基本步骤是什么?
审题、设元、列方程、解方程、检验作答
学会列表格法,理清思路。
谢谢大家!
同课章节目录
