人教版2021年八年级数学上册13.1《轴对称》同步练习卷(word版含答案)
文档属性
| 名称 | 人教版2021年八年级数学上册13.1《轴对称》同步练习卷(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 154.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览

文档简介
人教版2021年八年级数学上册:13.1《轴对称》同步练习卷
一.选择题
1.下列说法错误的有( )
A.关于某直线对称的两个图形一定能完全重合
B.全等的两个三角形一定关于某直线对称
C.轴对称图形的对称轴至少有一条
D.线段是轴对称图形
2.下面是科学防控新冠知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )
A.B.C.D.
3.在数学符号“+,﹣,×,÷,≈,=,≤,≥,( ),≠,∥中,轴对称图形有( )
A.5个 B.6个 C.7个 D.8个
4.下列对称轴条数最多的图形是( )
A.角 B.等边三角形 C.正方形 D.圆
5.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在( )
A.AC的垂直平分线上 B.∠BAC的平分线上
C.BC的中点 D.AB的垂直平分线上
6.如图,在Rt△ABC中,ED为AB的垂直平分线,连接CD,若∠B=52°,则∠ACD的度数为( )
A.38° B.48° C.52° D.42°
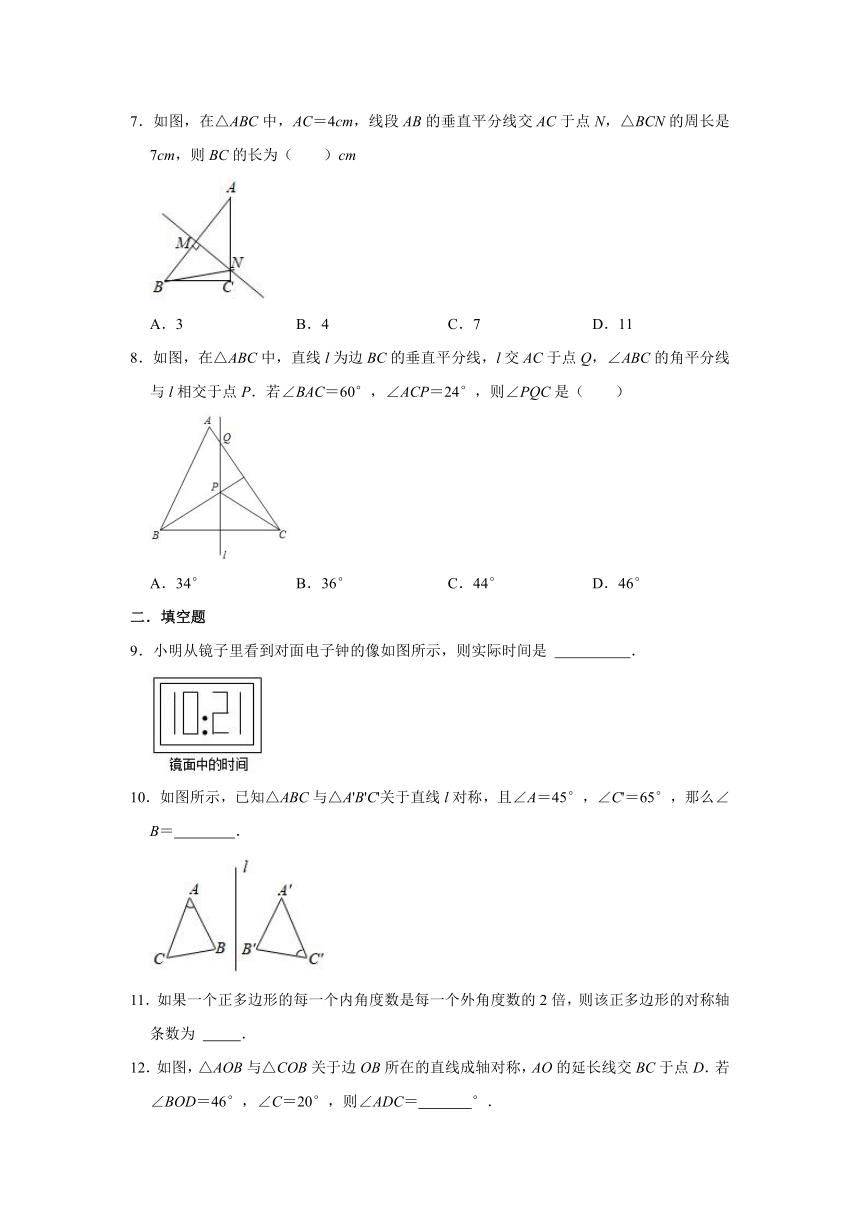
7.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )cm
A.3 B.4 C.7 D.11
8.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
二.填空题
9.小明从镜子里看到对面电子钟的像如图所示,则实际时间是 .
10.如图所示,已知△ABC与△A'B'C'关于直线l对称,且∠A=45°,∠C'=65°,那么∠B= .
11.如果一个正多边形的每一个内角度数是每一个外角度数的2倍,则该正多边形的对称轴条数为 .
12.如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=46°,∠C=20°,则∠ADC= °.
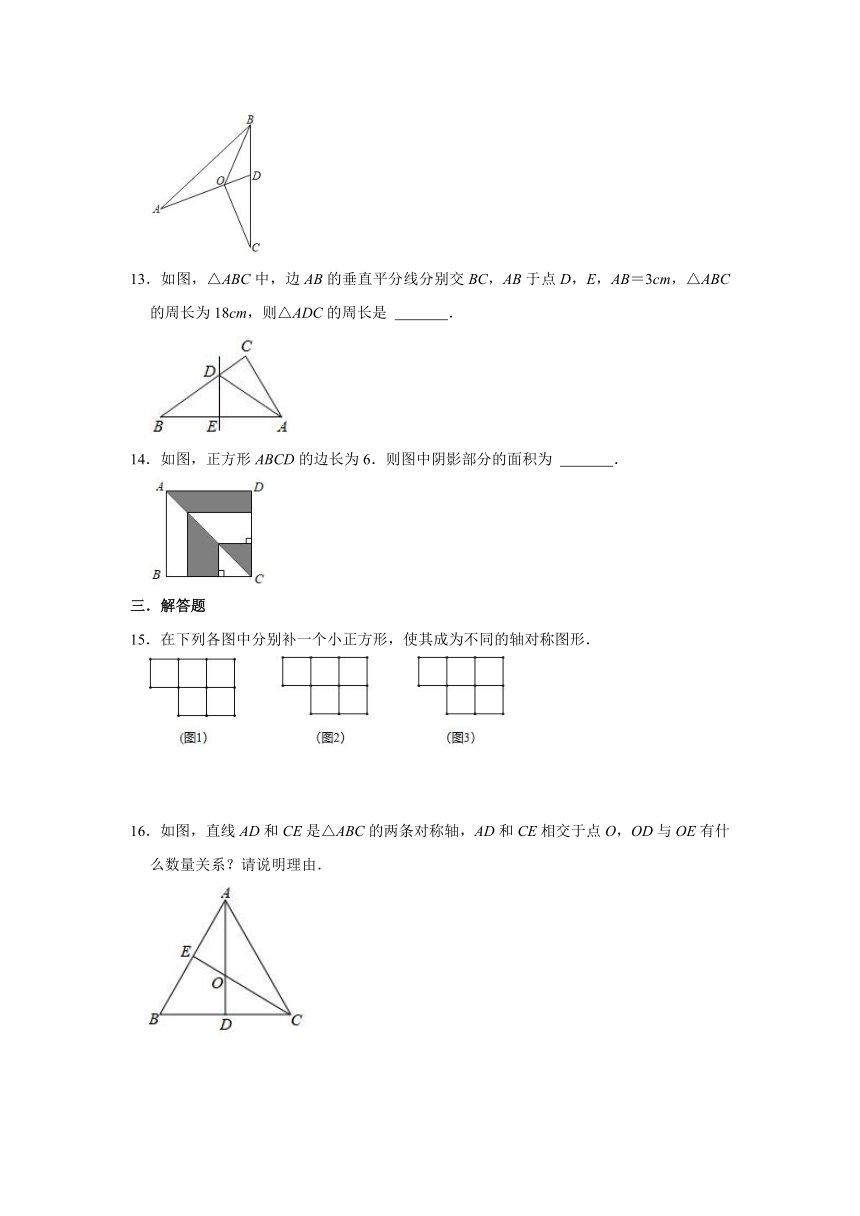
13.如图,△ABC中,边AB的垂直平分线分别交BC,AB于点D,E,AB=3cm,△ABC的周长为18cm,则△ADC的周长是 .
14.如图,正方形ABCD的边长为6.则图中阴影部分的面积为 .
三.解答题
15.在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.
16.如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD与OE有什么数量关系?请说明理由.
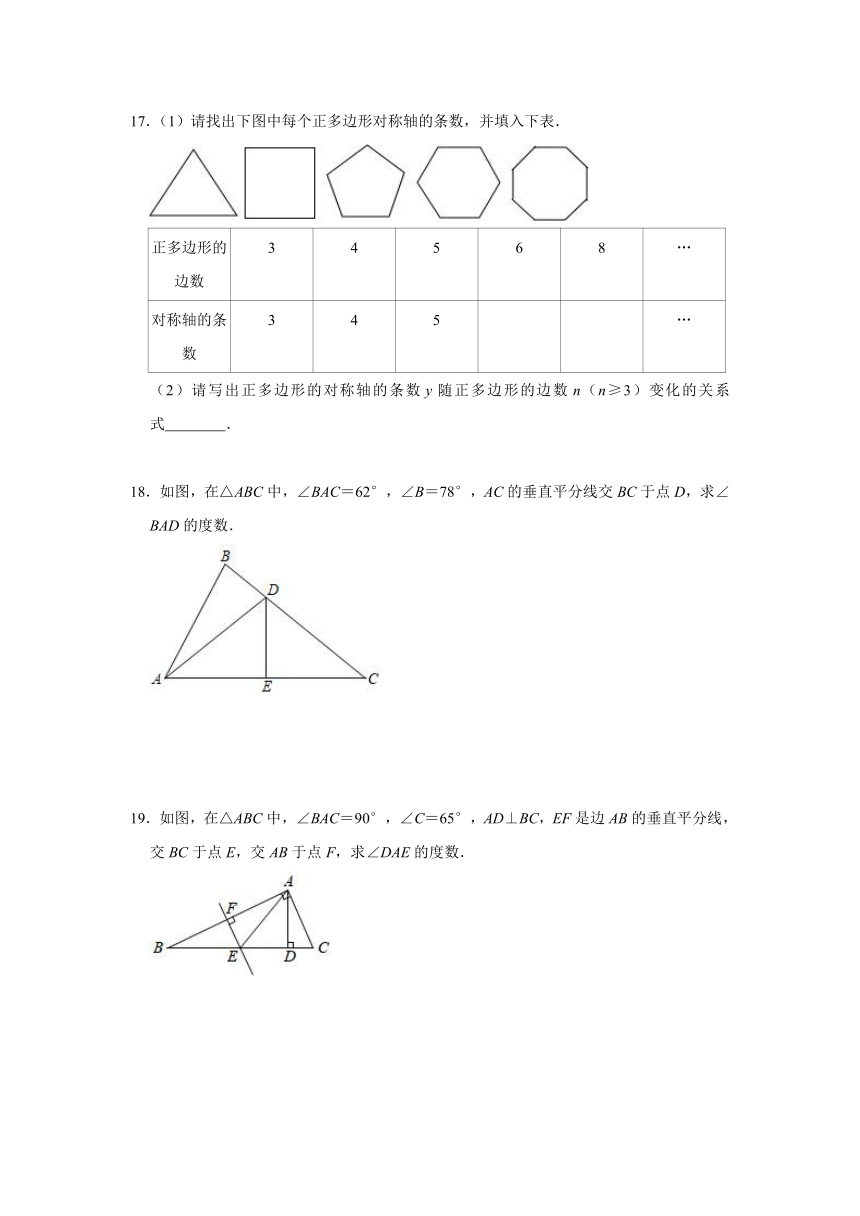
17.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数 3 4 5 6 8 …
对称轴的条数 3 4 5 …
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式 .
18.如图,在△ABC中,∠BAC=62°,∠B=78°,AC的垂直平分线交BC于点D,求∠BAD的度数.
19.如图,在△ABC中,∠BAC=90°,∠C=65°,AD⊥BC,EF是边AB的垂直平分线,交BC于点E,交AB于点F,求∠DAE的度数.
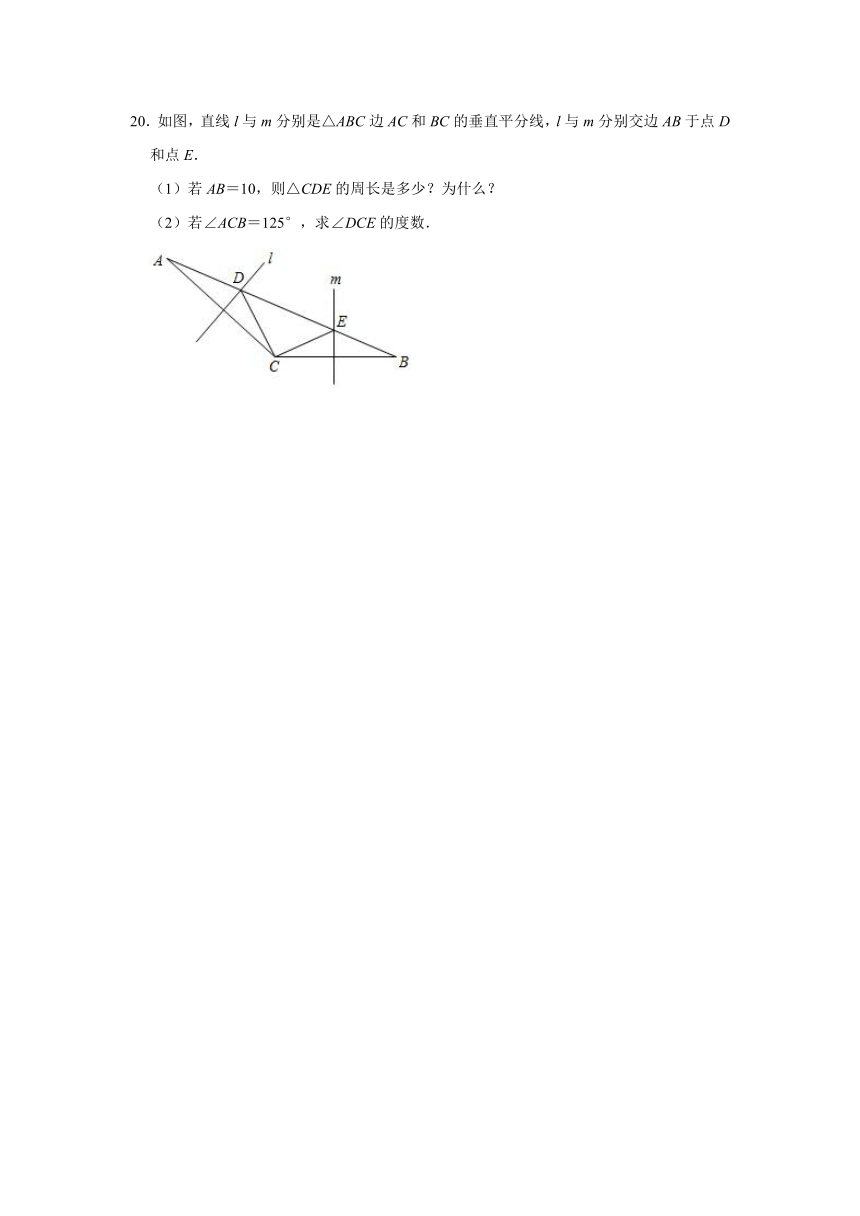
20.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
参考答案
一.选择题
1.解:A.关于某直线对称的两个图形一定能完全重合,正确,不合题意;
B.全等的两个三角形不一定关于某直线对称,原说法错误,符合题意;
C.轴对称图形的对称轴至少有一条,正确,不合题意;
D.线段是轴对称图形,正确,不合题意;
故选:B.
2.解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意.
故选:A.
3.解:在数学符号“+,﹣,×,÷,≈,=,≤,≥,( ),≠,∥中,轴对称图形有+,﹣,×,÷,=,( ),共6个.
故选:B.
4.解:A.角是轴对称图形,有1条对称轴;
B.等边三角形是轴对称图形,它有3条对称轴;
C.正方形是轴对称图形,有4条对称轴;
D.圆是轴对称图形,有无数条对称轴;
故对称轴条数最多的图形是圆.
故选:D.
5.解:∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,
故选:A.
6.解:∵ED为AB的垂直平分线,
∴AD=BD,
∵∠ACB=90°,
∴CD=BD,
∴∠DCB=∠B,
∵∠B=52°,
∴∠DCB=52°,
∴∠ACD=90°﹣52°=38°,
故选:A.
7.解:∵MN是线段AB的垂直平分线,
∴NA=NB,
∵△BCN的周长是7cm,
∴BC+CN+BN=7(cm),
∴BC+CN+NA=7(cm),即BC+AC=7(cm),
∵AC=4cm,
∴BC=3(cm),
故选:A.
8.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
二.填空题
9.解:根据镜面对称的性质,题中所显示的时刻与10:21成轴对称,所以此时实际时刻为15:01,
故答案为:15:01.
10.解:∵△ABC与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=65°,
∵∠A=45°,
∴∠B=180°﹣∠C﹣∠A
=180°﹣65°﹣45°
=70°.
故答案为:70°.
11.解:设该正多边形的每个外角为x°,
则2x+x=180,
解得x=60,
∵360÷60=6,
∴该正多边形为正六边形,
正六边形有6条对称轴,
故答案为:6.
12.解:∵△AOB与△COB关于边OB所在的直线成轴对称,
∴△AOB≌△COB,
∴∠A=∠C=20°,∠ABO=∠CBO,
∵∠BOD=∠A+∠ABO,
∴∠ABO=∠BOD﹣∠ABO=46°﹣20°=26°,
∴∠ABD=2∠ABO=52°,
∴∠ADC=∠A+∠ABD=20°+52°=72°,
故答案为:72.
13.解:∵△ABC的周长为18cm,
∴AB+BC+AC=18cm,
∵AB=3cm,
∴AC+BC=15cm,
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD=BC,
∴△ACD的周长=AC+CD+AD=AC+BC=15cm,
故答案为:15.
14.解:根据题意,得S阴影部分=S正方形ABCD=×62=18.
故答案为:18.
三.解答题
15.解:如图所示:
.
16.解:OD=OE.
理由如下:∵直线AD和CE是△ABC的两条对称轴,
∴AE=BE=AB,CD=BD=BC,CE⊥AB,AD⊥BC,
而AB=BC,
∴AE=CD,
在△AOE和△COD中
,
∴△AOE≌△COD(AAS),
∴OD=OE.
17.答(1)
正多边形的边数 3 4 5 6 8 …
对称轴的条数 3 4 5 6 8 …
故答案为:6,8.
解:(2)y=n(n≥3)
故答案为:y=n.
18.解:∵∠BAC=62°,∠B=78°,
∴∠C=180°﹣∠BAC﹣∠B=40°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=40°,
∴∠BAD=∠BAC﹣∠DAC=22°.
19.解:∵∠BAC=90°,∠C=65°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣90°﹣65°=25°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=25°,
∵EF是边AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=25°,
∴∠DAE=90°﹣25°﹣25°=40°.
20.解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
一.选择题
1.下列说法错误的有( )
A.关于某直线对称的两个图形一定能完全重合
B.全等的两个三角形一定关于某直线对称
C.轴对称图形的对称轴至少有一条
D.线段是轴对称图形
2.下面是科学防控新冠知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )
A.B.C.D.
3.在数学符号“+,﹣,×,÷,≈,=,≤,≥,( ),≠,∥中,轴对称图形有( )
A.5个 B.6个 C.7个 D.8个
4.下列对称轴条数最多的图形是( )
A.角 B.等边三角形 C.正方形 D.圆
5.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在( )
A.AC的垂直平分线上 B.∠BAC的平分线上
C.BC的中点 D.AB的垂直平分线上
6.如图,在Rt△ABC中,ED为AB的垂直平分线,连接CD,若∠B=52°,则∠ACD的度数为( )
A.38° B.48° C.52° D.42°
7.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )cm
A.3 B.4 C.7 D.11
8.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
二.填空题
9.小明从镜子里看到对面电子钟的像如图所示,则实际时间是 .
10.如图所示,已知△ABC与△A'B'C'关于直线l对称,且∠A=45°,∠C'=65°,那么∠B= .
11.如果一个正多边形的每一个内角度数是每一个外角度数的2倍,则该正多边形的对称轴条数为 .
12.如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=46°,∠C=20°,则∠ADC= °.
13.如图,△ABC中,边AB的垂直平分线分别交BC,AB于点D,E,AB=3cm,△ABC的周长为18cm,则△ADC的周长是 .
14.如图,正方形ABCD的边长为6.则图中阴影部分的面积为 .
三.解答题
15.在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.
16.如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD与OE有什么数量关系?请说明理由.
17.(1)请找出下图中每个正多边形对称轴的条数,并填入下表.
正多边形的边数 3 4 5 6 8 …
对称轴的条数 3 4 5 …
(2)请写出正多边形的对称轴的条数y随正多边形的边数n(n≥3)变化的关系式 .
18.如图,在△ABC中,∠BAC=62°,∠B=78°,AC的垂直平分线交BC于点D,求∠BAD的度数.
19.如图,在△ABC中,∠BAC=90°,∠C=65°,AD⊥BC,EF是边AB的垂直平分线,交BC于点E,交AB于点F,求∠DAE的度数.
20.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
参考答案
一.选择题
1.解:A.关于某直线对称的两个图形一定能完全重合,正确,不合题意;
B.全等的两个三角形不一定关于某直线对称,原说法错误,符合题意;
C.轴对称图形的对称轴至少有一条,正确,不合题意;
D.线段是轴对称图形,正确,不合题意;
故选:B.
2.解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意.
故选:A.
3.解:在数学符号“+,﹣,×,÷,≈,=,≤,≥,( ),≠,∥中,轴对称图形有+,﹣,×,÷,=,( ),共6个.
故选:B.
4.解:A.角是轴对称图形,有1条对称轴;
B.等边三角形是轴对称图形,它有3条对称轴;
C.正方形是轴对称图形,有4条对称轴;
D.圆是轴对称图形,有无数条对称轴;
故对称轴条数最多的图形是圆.
故选:D.
5.解:∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,
故选:A.
6.解:∵ED为AB的垂直平分线,
∴AD=BD,
∵∠ACB=90°,
∴CD=BD,
∴∠DCB=∠B,
∵∠B=52°,
∴∠DCB=52°,
∴∠ACD=90°﹣52°=38°,
故选:A.
7.解:∵MN是线段AB的垂直平分线,
∴NA=NB,
∵△BCN的周长是7cm,
∴BC+CN+BN=7(cm),
∴BC+CN+NA=7(cm),即BC+AC=7(cm),
∵AC=4cm,
∴BC=3(cm),
故选:A.
8.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
二.填空题
9.解:根据镜面对称的性质,题中所显示的时刻与10:21成轴对称,所以此时实际时刻为15:01,
故答案为:15:01.
10.解:∵△ABC与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=65°,
∵∠A=45°,
∴∠B=180°﹣∠C﹣∠A
=180°﹣65°﹣45°
=70°.
故答案为:70°.
11.解:设该正多边形的每个外角为x°,
则2x+x=180,
解得x=60,
∵360÷60=6,
∴该正多边形为正六边形,
正六边形有6条对称轴,
故答案为:6.
12.解:∵△AOB与△COB关于边OB所在的直线成轴对称,
∴△AOB≌△COB,
∴∠A=∠C=20°,∠ABO=∠CBO,
∵∠BOD=∠A+∠ABO,
∴∠ABO=∠BOD﹣∠ABO=46°﹣20°=26°,
∴∠ABD=2∠ABO=52°,
∴∠ADC=∠A+∠ABD=20°+52°=72°,
故答案为:72.
13.解:∵△ABC的周长为18cm,
∴AB+BC+AC=18cm,
∵AB=3cm,
∴AC+BC=15cm,
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD=BC,
∴△ACD的周长=AC+CD+AD=AC+BC=15cm,
故答案为:15.
14.解:根据题意,得S阴影部分=S正方形ABCD=×62=18.
故答案为:18.
三.解答题
15.解:如图所示:
.
16.解:OD=OE.
理由如下:∵直线AD和CE是△ABC的两条对称轴,
∴AE=BE=AB,CD=BD=BC,CE⊥AB,AD⊥BC,
而AB=BC,
∴AE=CD,
在△AOE和△COD中
,
∴△AOE≌△COD(AAS),
∴OD=OE.
17.答(1)
正多边形的边数 3 4 5 6 8 …
对称轴的条数 3 4 5 6 8 …
故答案为:6,8.
解:(2)y=n(n≥3)
故答案为:y=n.
18.解:∵∠BAC=62°,∠B=78°,
∴∠C=180°﹣∠BAC﹣∠B=40°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=40°,
∴∠BAD=∠BAC﹣∠DAC=22°.
19.解:∵∠BAC=90°,∠C=65°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣90°﹣65°=25°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=25°,
∵EF是边AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=25°,
∴∠DAE=90°﹣25°﹣25°=40°.
20.解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
