五年级上册教案 2.4多边形的面积计算 苏教版
文档属性
| 名称 | 五年级上册教案 2.4多边形的面积计算 苏教版 |  | |
| 格式 | zip | ||
| 文件大小 | 181.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-22 22:27:23 | ||
图片预览

文档简介
五年级上册数学教案
2.4多边形的面积计算
本章节解读:本章节主要内容为五年级多边形面积的计算中第四课时多边形的面积公式计算及单位换算,本章节涉及到转化、归纳的思维方式,通过添加辅助线等方式,把多边形的面积问题转化为已经学过的、常见的特殊图形的面积,再进行计算,求解。
知识与技能目标:使学生通过平移、旋转、剪拼等方法,探索并掌握三角形、平行四边形和梯形的面积计算公式,能够利用公式正确的计算它们的面积。
过程与方法:使学生通过操作、列表、观察、分析等数学活动,体会变形、转化等数学思想,开展初步的空间想象能力和推理能力。
情感态度和价值观:使学生在操作、思考问题的过程中,提高空间想象能力和推理能力,感受数学的魅力,逐步形成数学情感。
教学重点:平行四边形、三角形、梯形的面积计算公式。
教学难点:理解三种面积计算公式的推导过程,熟练运算公式解决问题。
教学过程:
一:复习导入
教师提问:同学们,回想一下,我们已经学习过哪些图形?这些图形的面积又是如何推出来的?(指导学生进行小组讨论,之后派代表进行回答)(学生答:平行四边形的面积、三角形的面积和梯形的面积,将平行四边形切割成长方形,之后推导出来,将平行四边形切成两个三角形再计算面积,将两个一样的平行四边形组成一个梯形。)
教师归纳:同学们说的都很对,我们在学习平行四边形和三角形的面积公式和梯形的面积公式就是XX同学说的那样推导出来的。今天,老师带领大家复习一下我们上几节课学习的内容以及它们组合起来的图形面积计算方法。(教师板书:多边形的面积计算)
二:新知探究
巩固旧识
填一填:文字和字母分别表示出来。
图形 长 宽(高) 面积
长方形
平行四边形
三角形
梯形
2.图形导入
3.教师引导
同学们思考一下,这些公式推导过程中,都有哪些相同点和哪些不同点?
学生思考问题,并做出适当答案(引导学生进行发散性思维训练,不仅仅是本学科学习内容,也有自己的思想方法,教师根据学生回答进行总结归纳和整理,输出一个比较满意的回答。)
教师归纳:(表扬)学生从不同角度、不同方式,利用所学知识,创造性的解决问题。同时点明出推导过程中均使用了“转化”思想,把未知图形的问题转化为已知图形的面积的问题,通过已掌握公式进行求解。(教师板书:转化)
教师提问:同学们,如果我将一个三角形和一个长方形的图形组合一起,那么你们还会不会求这个特殊图形的面积?
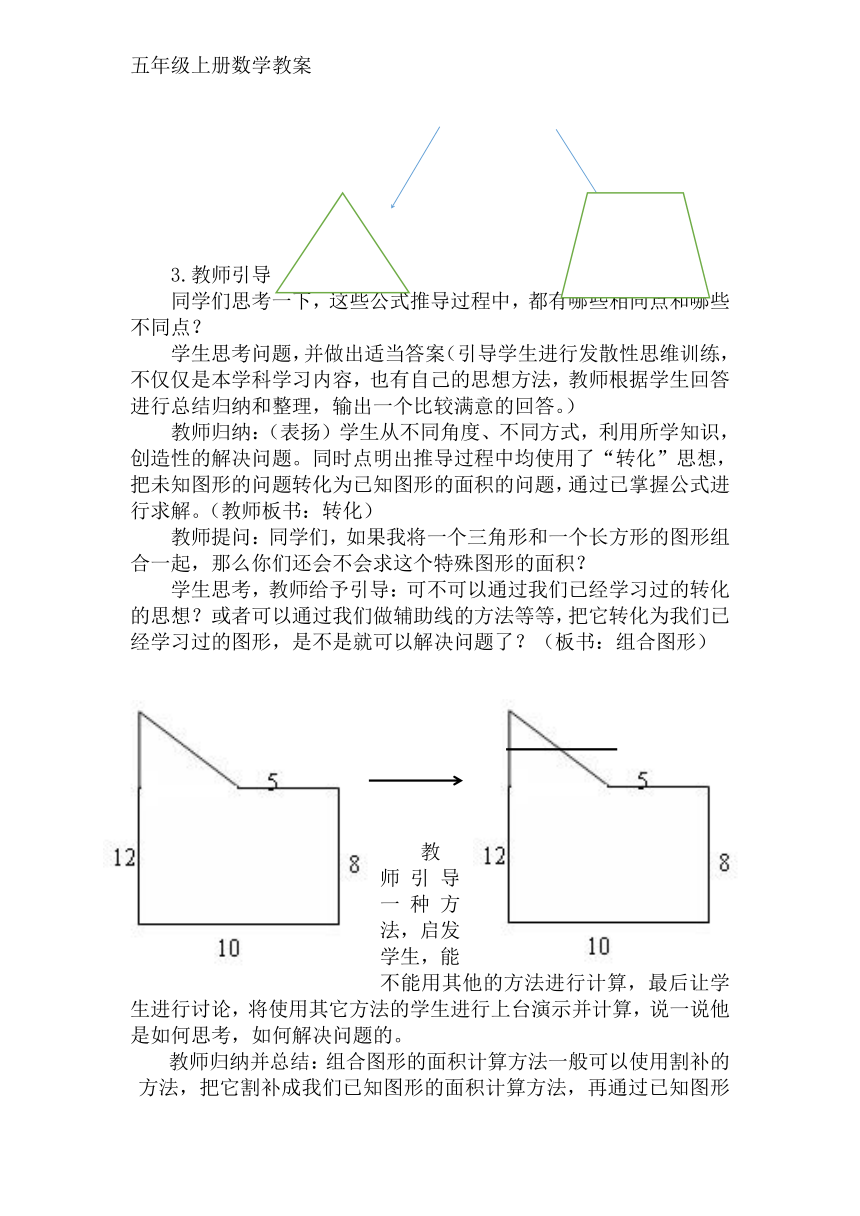
学生思考,教师给予引导:可不可以通过我们已经学习过的转化的思想?或者可以通过我们做辅助线的方法等等,把它转化为我们已经学习过的图形,是不是就可以解决问题了?(板书:组合图形)
教师引导一种方法,启发学生,能不能用其他的方法进行计算,最后让学生进行讨论,将使用其它方法的学生进行上台演示并计算,说一说他是如何思考,如何解决问题的。
教师归纳并总结:组合图形的面积计算方法一般可以使用割补的方法,把它割补成我们已知图形的面积计算方法,再通过已知图形的面积计算方法求出未知图形,这样就是多边形的面积计算方法。但是在进行分割或者补充时候,需要注意的是图形本事割补的方法能否适用。
三,巩固新知
例1、寻找合适的条件,利用公式求出图形中多边形的面积。
4cm
4cm 4cm
5cm 5cm 5cm 2cm
5cm 10cm
例2、正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?
例3.求下图阴影部分的面积(单位:厘米)。
例4、如下图所示,用 36 厘米的篱笆靠墙围一块菜地,那么菜地的面积是多少
四合作探究
右图是一块长方形草地,长方形长为16,宽为12,中间有一条宽为2的道路,求草地(阴影部分)的面积。
课堂总结
本节课,各位同学都表现的非常棒,哪位同学说一说这节课你学到了什么?
通过学习,课后去发现生活中还有哪些实例可以用到组合图形面积计算?
六.课后作业
书本课后习题。
七:板书设计
组合图形
转化思想
多边形的面积计算
2.4多边形的面积计算
本章节解读:本章节主要内容为五年级多边形面积的计算中第四课时多边形的面积公式计算及单位换算,本章节涉及到转化、归纳的思维方式,通过添加辅助线等方式,把多边形的面积问题转化为已经学过的、常见的特殊图形的面积,再进行计算,求解。
知识与技能目标:使学生通过平移、旋转、剪拼等方法,探索并掌握三角形、平行四边形和梯形的面积计算公式,能够利用公式正确的计算它们的面积。
过程与方法:使学生通过操作、列表、观察、分析等数学活动,体会变形、转化等数学思想,开展初步的空间想象能力和推理能力。
情感态度和价值观:使学生在操作、思考问题的过程中,提高空间想象能力和推理能力,感受数学的魅力,逐步形成数学情感。
教学重点:平行四边形、三角形、梯形的面积计算公式。
教学难点:理解三种面积计算公式的推导过程,熟练运算公式解决问题。
教学过程:
一:复习导入
教师提问:同学们,回想一下,我们已经学习过哪些图形?这些图形的面积又是如何推出来的?(指导学生进行小组讨论,之后派代表进行回答)(学生答:平行四边形的面积、三角形的面积和梯形的面积,将平行四边形切割成长方形,之后推导出来,将平行四边形切成两个三角形再计算面积,将两个一样的平行四边形组成一个梯形。)
教师归纳:同学们说的都很对,我们在学习平行四边形和三角形的面积公式和梯形的面积公式就是XX同学说的那样推导出来的。今天,老师带领大家复习一下我们上几节课学习的内容以及它们组合起来的图形面积计算方法。(教师板书:多边形的面积计算)
二:新知探究
巩固旧识
填一填:文字和字母分别表示出来。
图形 长 宽(高) 面积
长方形
平行四边形
三角形
梯形
2.图形导入
3.教师引导
同学们思考一下,这些公式推导过程中,都有哪些相同点和哪些不同点?
学生思考问题,并做出适当答案(引导学生进行发散性思维训练,不仅仅是本学科学习内容,也有自己的思想方法,教师根据学生回答进行总结归纳和整理,输出一个比较满意的回答。)
教师归纳:(表扬)学生从不同角度、不同方式,利用所学知识,创造性的解决问题。同时点明出推导过程中均使用了“转化”思想,把未知图形的问题转化为已知图形的面积的问题,通过已掌握公式进行求解。(教师板书:转化)
教师提问:同学们,如果我将一个三角形和一个长方形的图形组合一起,那么你们还会不会求这个特殊图形的面积?
学生思考,教师给予引导:可不可以通过我们已经学习过的转化的思想?或者可以通过我们做辅助线的方法等等,把它转化为我们已经学习过的图形,是不是就可以解决问题了?(板书:组合图形)
教师引导一种方法,启发学生,能不能用其他的方法进行计算,最后让学生进行讨论,将使用其它方法的学生进行上台演示并计算,说一说他是如何思考,如何解决问题的。
教师归纳并总结:组合图形的面积计算方法一般可以使用割补的方法,把它割补成我们已知图形的面积计算方法,再通过已知图形的面积计算方法求出未知图形,这样就是多边形的面积计算方法。但是在进行分割或者补充时候,需要注意的是图形本事割补的方法能否适用。
三,巩固新知
例1、寻找合适的条件,利用公式求出图形中多边形的面积。
4cm
4cm 4cm
5cm 5cm 5cm 2cm
5cm 10cm
例2、正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?
例3.求下图阴影部分的面积(单位:厘米)。
例4、如下图所示,用 36 厘米的篱笆靠墙围一块菜地,那么菜地的面积是多少
四合作探究
右图是一块长方形草地,长方形长为16,宽为12,中间有一条宽为2的道路,求草地(阴影部分)的面积。
课堂总结
本节课,各位同学都表现的非常棒,哪位同学说一说这节课你学到了什么?
通过学习,课后去发现生活中还有哪些实例可以用到组合图形面积计算?
六.课后作业
书本课后习题。
七:板书设计
组合图形
转化思想
多边形的面积计算
