华东师大版七上数学 4.6.3余角和补角 课件(共23张PPT)
文档属性
| 名称 | 华东师大版七上数学 4.6.3余角和补角 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 697.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 10:23:04 | ||
图片预览





文档简介
(共23张PPT)
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
问题
你能帮他解决这个问题吗?
4.6 角
学习目标:
1.了解余角、补角的概念。
2.掌握余角、补角的性质。
3.运用本节所学知识解决简单的实际问题。
4. 与小组同伴主动交流自己在学习中的收获和问题,共同学习,共同进步。
预习检测
什么叫互为余角?
什么叫互为补角?
余角,补角的性质
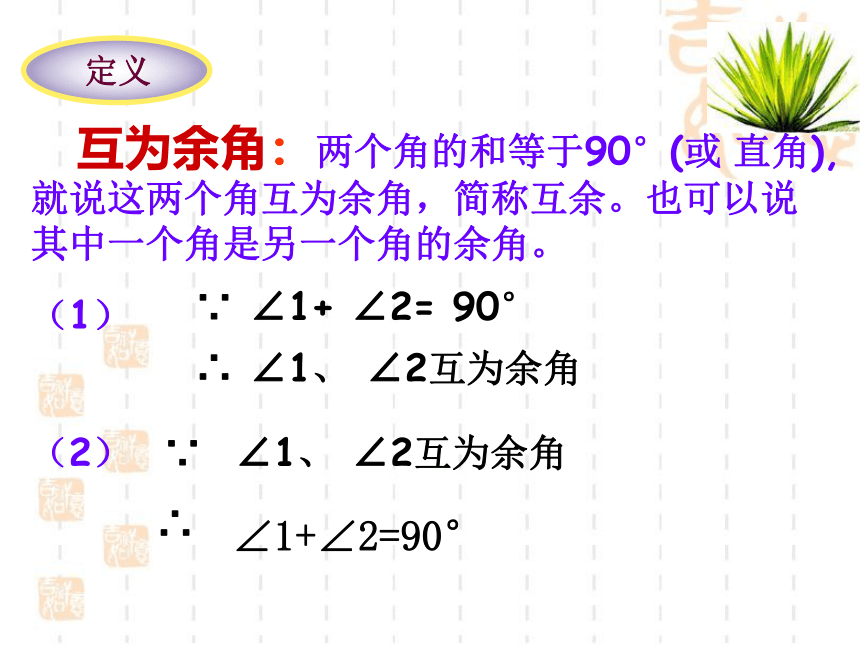
13°15′
76°45′
37°
53°
·
1
2
2
1
1
2
探究新知
这两个角的和是多少?
定义
互为余角:两个角的和等于90°(或 直角),就说这两个角互为余角,简称互余。也可以说其中一个角是另一个角的余角。
(1)
(2) ∵ ∠1、 ∠2互为余角
∴ ∠1+∠2=90°
∵ ∠1+ ∠2= 90°
∴ ∠1、 ∠2互为余角
2
1
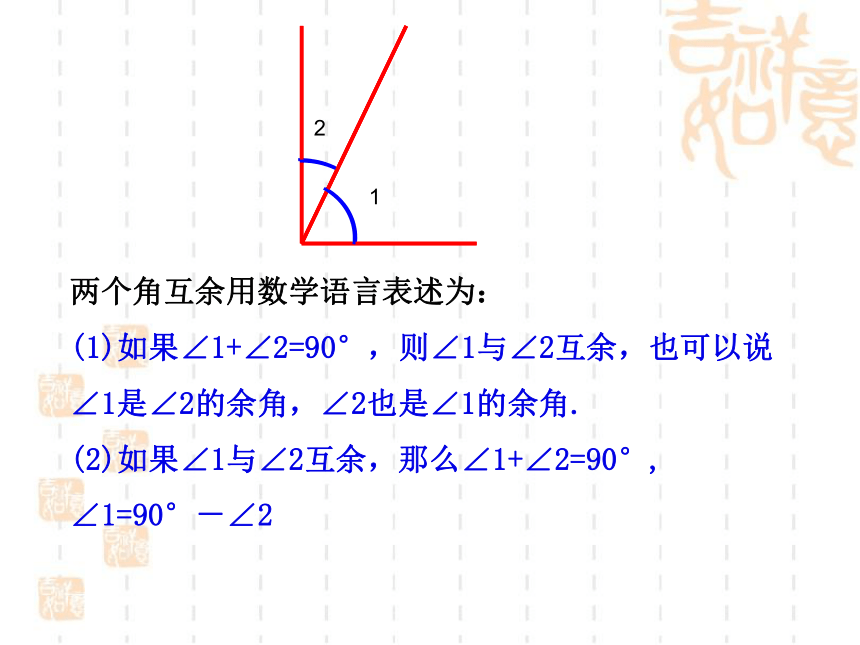
两个角互余用数学语言表述为:
(1)如果∠1+∠2=90°,则∠1与∠2互余,也可以说∠1是∠2的余角,∠2也是∠1的余角.
(2)如果∠1与∠2互余,那么∠1+∠2=90°,
∠1=90°-∠2
55°26′
124°34′
30°
150°
·
3
4
这两个角的和是多少?
定义二
互为补角:如果两个角的和等于180°(或平角),就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角
∵ ∠1+ ∠2= 180°
∴ ∠1、 ∠2互为补角
注意事项:互余和互补的两个角只与它们的数量有关,与位置无关。
两个角互补用数学语言表述为:
(1)如果∠1+∠2=180°,则∠1与∠2互补,也可以说∠1是∠2的补角,∠2也是∠1的补角.
(2)如果∠1与∠2互补,那么∠1+∠2=180°,
∠1=180°-∠2
1
2
请同学们比较互补与互余的概念,说说它们的区别和共同之处?
区别:互余是两个角的和是直角,互补是两个角的和是平角.
相同:(1)互余和互补都是对两个角而言;
(2)不管这两个角在什么位置,只要满足两角和是
90度(180度),它们都互余(补)
(角的数量特点)
例题讲解
已知∠α=50°17′,求∠α的余角和补角。
解:∠α的余角=90°-50°17′= 39°43′,
∠α的补角=180°-50°17′= 129°43′。
C
O
B
1、 画出∠COB的余角,并猜想它们有什么关系
2、 画出∠COB的补角,并猜想它们有什么关系
1、 画出∠COB的余角,并猜想它们有什么关系
C
O
B
A
D
解:∵ ∠1+ ∠BOC = 90 °
∠2+ ∠BOC = 90 °
∴ ∠1= 90 °- ∠BOC
∠2= 90 °- ∠BOC
∴∠1 = ∠2
1
2
同角的余角相等
探究一
如图,∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解: ∠2与∠4相等
∵ ∠1﹢∠2 = 90°, ∠3﹢∠4 = 90°
∴ ∠2 = , ∠4 = ,
∵ ∠1 =∠3
∴ ∠2 =∠4
等角的余角相等
90°-∠1
90°-∠3
性质
1、余角的性质
同角(等角)的余角相等
2、补角的性质
同角(等角)的补角相等
补角具有同样的性质吗?
A
B
C
D
要测量两堵墙所成的角AOB的度数,但人不能进入围墙,如何测量
答疑解惑
1、填空:
①若∠1与∠2互余,则∠1+∠2=______;
②若∠1=180°-∠2,则∠1与∠2________;
③30°的余角是____,补角是_____若一个角的度
数是x(x<90°) ,则它的余角的度数和补角的度数分
别是______________________________;
④60°角的余角的补角是_________.
②若∠AOD=53°13′,则∠DOC= ,∠BOD= .
90°
互补
60°
150°
(90 - x)°和(180 - x)°
150°
126°47'
36°47'
√
╳
╳
2、 判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角
3、O是直线AB上的一点,OC是∠AOB的平分线.
看图回答: ①图中互余的角是 ,图中互补的角是 ;
∠AOD与∠DOC
∠AOD与∠DOB、
C
D
·
O
B
A
∠AOC与∠BOC
4、 如右图,已知∠AOC=∠BOD=90°.
(1)指出图中∠BOC的余角
(2)找出图中还有哪些角相等
C
A
D
B
O
2、 已知∠3=140°,并且∠1=∠2。求∠4的度数。
1
2
3
4
应用拓展
课堂小结
本节课我们学习的主要内容是什么?
2个定义
互为余角
互为补角
2个性质
余角的性质 同角(等角)的余角相等
补角的性质 同角(等角)的补角相等
同学们,你们学会了吗?
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
问题
你能帮他解决这个问题吗?
4.6 角
学习目标:
1.了解余角、补角的概念。
2.掌握余角、补角的性质。
3.运用本节所学知识解决简单的实际问题。
4. 与小组同伴主动交流自己在学习中的收获和问题,共同学习,共同进步。
预习检测
什么叫互为余角?
什么叫互为补角?
余角,补角的性质
13°15′
76°45′
37°
53°
·
1
2
2
1
1
2
探究新知
这两个角的和是多少?
定义
互为余角:两个角的和等于90°(或 直角),就说这两个角互为余角,简称互余。也可以说其中一个角是另一个角的余角。
(1)
(2) ∵ ∠1、 ∠2互为余角
∴ ∠1+∠2=90°
∵ ∠1+ ∠2= 90°
∴ ∠1、 ∠2互为余角
2
1
两个角互余用数学语言表述为:
(1)如果∠1+∠2=90°,则∠1与∠2互余,也可以说∠1是∠2的余角,∠2也是∠1的余角.
(2)如果∠1与∠2互余,那么∠1+∠2=90°,
∠1=90°-∠2
55°26′
124°34′
30°
150°
·
3
4
这两个角的和是多少?
定义二
互为补角:如果两个角的和等于180°(或平角),就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角
∵ ∠1+ ∠2= 180°
∴ ∠1、 ∠2互为补角
注意事项:互余和互补的两个角只与它们的数量有关,与位置无关。
两个角互补用数学语言表述为:
(1)如果∠1+∠2=180°,则∠1与∠2互补,也可以说∠1是∠2的补角,∠2也是∠1的补角.
(2)如果∠1与∠2互补,那么∠1+∠2=180°,
∠1=180°-∠2
1
2
请同学们比较互补与互余的概念,说说它们的区别和共同之处?
区别:互余是两个角的和是直角,互补是两个角的和是平角.
相同:(1)互余和互补都是对两个角而言;
(2)不管这两个角在什么位置,只要满足两角和是
90度(180度),它们都互余(补)
(角的数量特点)
例题讲解
已知∠α=50°17′,求∠α的余角和补角。
解:∠α的余角=90°-50°17′= 39°43′,
∠α的补角=180°-50°17′= 129°43′。
C
O
B
1、 画出∠COB的余角,并猜想它们有什么关系
2、 画出∠COB的补角,并猜想它们有什么关系
1、 画出∠COB的余角,并猜想它们有什么关系
C
O
B
A
D
解:∵ ∠1+ ∠BOC = 90 °
∠2+ ∠BOC = 90 °
∴ ∠1= 90 °- ∠BOC
∠2= 90 °- ∠BOC
∴∠1 = ∠2
1
2
同角的余角相等
探究一
如图,∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解: ∠2与∠4相等
∵ ∠1﹢∠2 = 90°, ∠3﹢∠4 = 90°
∴ ∠2 = , ∠4 = ,
∵ ∠1 =∠3
∴ ∠2 =∠4
等角的余角相等
90°-∠1
90°-∠3
性质
1、余角的性质
同角(等角)的余角相等
2、补角的性质
同角(等角)的补角相等
补角具有同样的性质吗?
A
B
C
D
要测量两堵墙所成的角AOB的度数,但人不能进入围墙,如何测量
答疑解惑
1、填空:
①若∠1与∠2互余,则∠1+∠2=______;
②若∠1=180°-∠2,则∠1与∠2________;
③30°的余角是____,补角是_____若一个角的度
数是x(x<90°) ,则它的余角的度数和补角的度数分
别是______________________________;
④60°角的余角的补角是_________.
②若∠AOD=53°13′,则∠DOC= ,∠BOD= .
90°
互补
60°
150°
(90 - x)°和(180 - x)°
150°
126°47'
36°47'
√
╳
╳
2、 判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角
3、O是直线AB上的一点,OC是∠AOB的平分线.
看图回答: ①图中互余的角是 ,图中互补的角是 ;
∠AOD与∠DOC
∠AOD与∠DOB、
C
D
·
O
B
A
∠AOC与∠BOC
4、 如右图,已知∠AOC=∠BOD=90°.
(1)指出图中∠BOC的余角
(2)找出图中还有哪些角相等
C
A
D
B
O
2、 已知∠3=140°,并且∠1=∠2。求∠4的度数。
1
2
3
4
应用拓展
课堂小结
本节课我们学习的主要内容是什么?
2个定义
互为余角
互为补角
2个性质
余角的性质 同角(等角)的余角相等
补角的性质 同角(等角)的补角相等
同学们,你们学会了吗?
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
