2021-2022学年数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 21:19:54 | ||
图片预览




文档简介
(共16张PPT)
2.1.1直线的倾斜角与斜率
一、情景引入
请同学们观察图片,说说图片中的直线有什么区别?
思考:在平面直角坐标系中,如何确定一条直线的位置?
在平面直角坐标系中,由一点能否确定一条直线?
两点可以确定一条直线
不能
直线的方向不同
二、探究新知
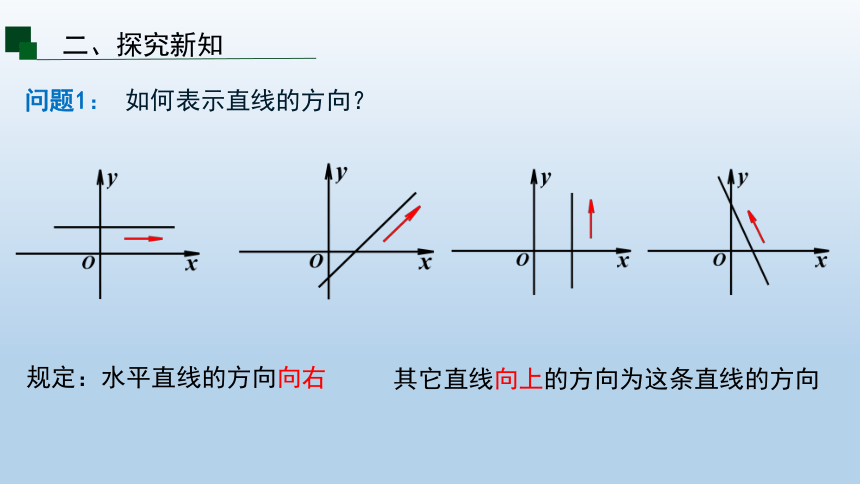
问题1: 如何表示直线的方向?
规定:水平直线的方向向右
其它直线向上的方向为这条直线的方向
二、探究新知
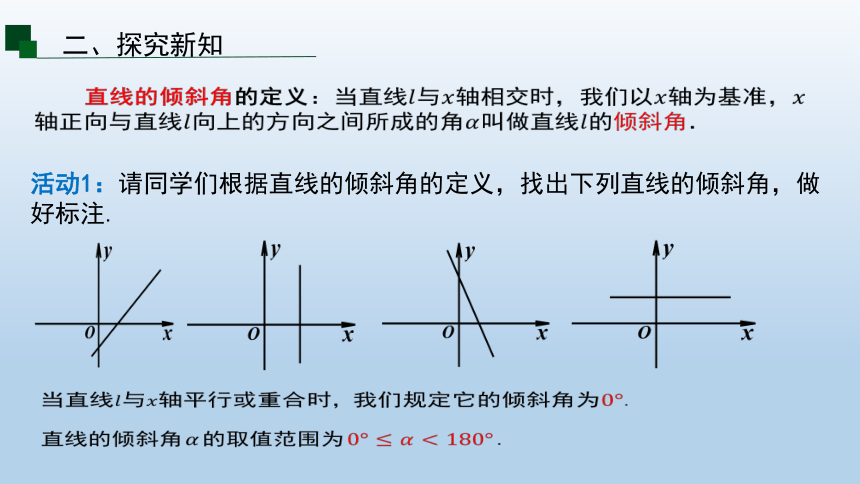
活动1:请同学们根据直线的倾斜角的定义,找出下列直线的倾斜角,做好标注.
二、探究新知
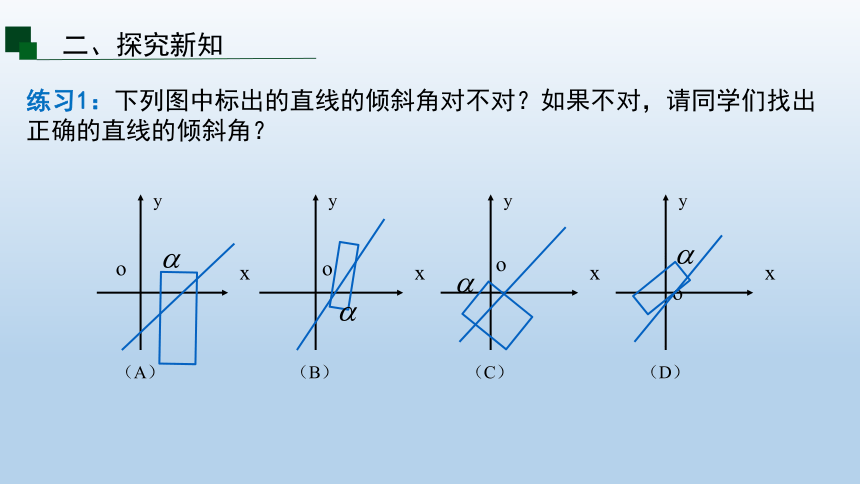
练习1:下列图中标出的直线的倾斜角对不对?如果不对,请同学们找出正确的直线的倾斜角?
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
二、探究新知
直线OP的倾斜角为α.
由正切函数的定义,有
二、探究新知
直线OP的倾斜角为α.
P的坐标为(x2-x1,y2-y1)
直线OP的倾斜角为α
二、探究新知
结论: 直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2)(x1 x2)的坐标有如下关系:
直线的斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
二、探究新知
例1 已知下列直线的倾斜角,求直线的斜率.
二、探究新知
例2 已知下列直线的斜率,求直线的倾斜角.
二、探究新知
例3 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
二、探究新知
问题:直线的倾斜角和斜率之间的关系
二、探究新知
(1)直线的倾斜角的定义以及如何找直线的倾斜角.
(2)直线的斜率.
(3)直线的倾斜角,斜率,直线上两点坐标之间的关系.
三、课堂小结
课本57页习题2.1第1、2、3题.
四、作业布置
2.1.1直线的倾斜角与斜率
一、情景引入
请同学们观察图片,说说图片中的直线有什么区别?
思考:在平面直角坐标系中,如何确定一条直线的位置?
在平面直角坐标系中,由一点能否确定一条直线?
两点可以确定一条直线
不能
直线的方向不同
二、探究新知
问题1: 如何表示直线的方向?
规定:水平直线的方向向右
其它直线向上的方向为这条直线的方向
二、探究新知
活动1:请同学们根据直线的倾斜角的定义,找出下列直线的倾斜角,做好标注.
二、探究新知
练习1:下列图中标出的直线的倾斜角对不对?如果不对,请同学们找出正确的直线的倾斜角?
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
二、探究新知
直线OP的倾斜角为α.
由正切函数的定义,有
二、探究新知
直线OP的倾斜角为α.
P的坐标为(x2-x1,y2-y1)
直线OP的倾斜角为α
二、探究新知
结论: 直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2)(x1 x2)的坐标有如下关系:
直线的斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
二、探究新知
例1 已知下列直线的倾斜角,求直线的斜率.
二、探究新知
例2 已知下列直线的斜率,求直线的倾斜角.
二、探究新知
例3 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
二、探究新知
问题:直线的倾斜角和斜率之间的关系
二、探究新知
(1)直线的倾斜角的定义以及如何找直线的倾斜角.
(2)直线的斜率.
(3)直线的倾斜角,斜率,直线上两点坐标之间的关系.
三、课堂小结
课本57页习题2.1第1、2、3题.
四、作业布置
